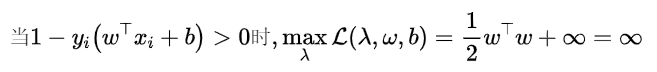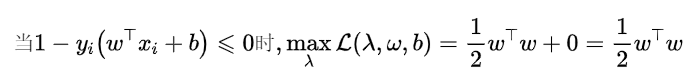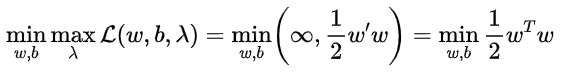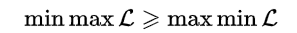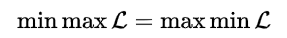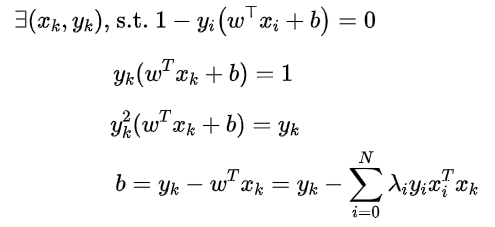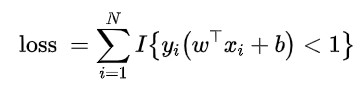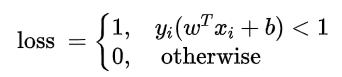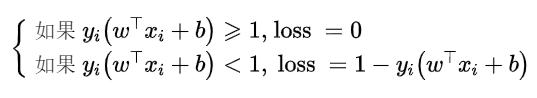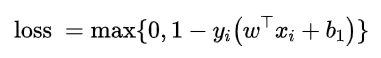支持向量机（Support Vector Machine）

介绍

深度学习流行之前，支持向量机是被广泛使用的分类算法
SVM有三宝：间隔、对偶、核技巧
SVM分类：

• hard-margin SVM
• soft-margin SVM
• kernel SVM

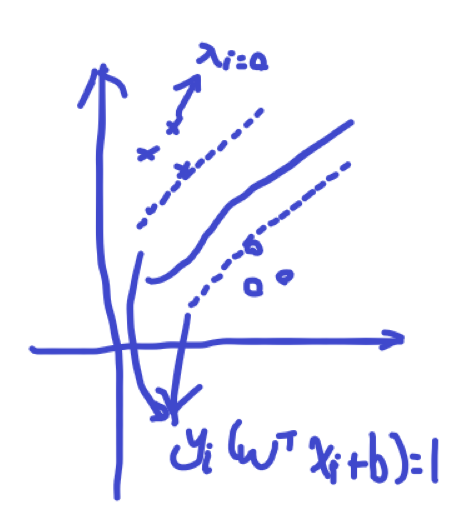
SVM本质上是一个判别模型，其函数及示例如图所示：

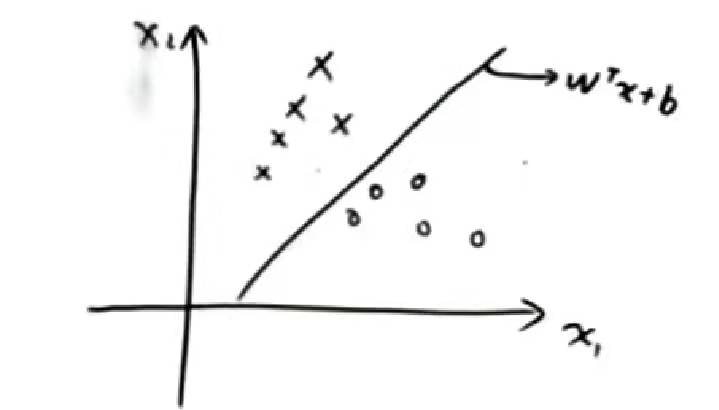
其中的直线可以设为判别模型：

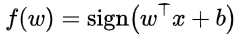
目标：从这么多的分类直线中找出最好的（鲁棒性强的）一条直线
出发点：直线的鲁棒性，使其与样本点的距离足够大

硬间隔SVM

模型定义

最大间隔器[max margin(w,b)]，它基于公式

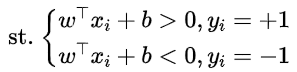
这个式子组可以进一步写成：

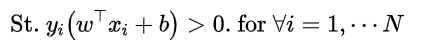
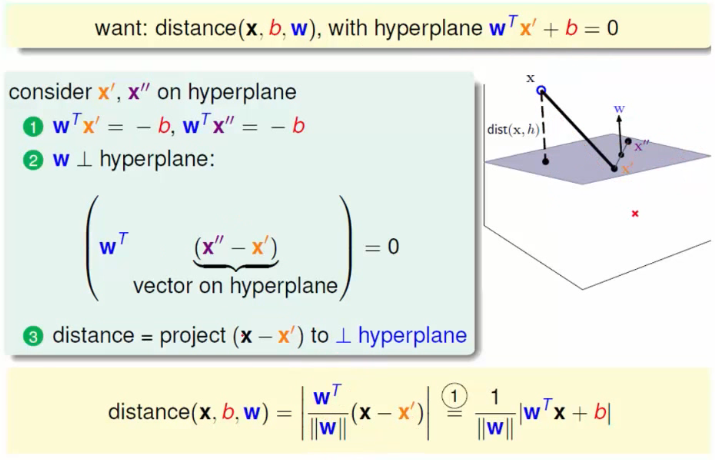
于是，为了得到最大间隔器，求得数据点与边界线的距离，并使该距离最小化，可以得到，
\

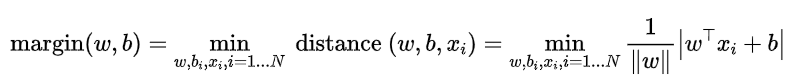得到该距离公式的方法为：

进一步化简并结合可以得到，

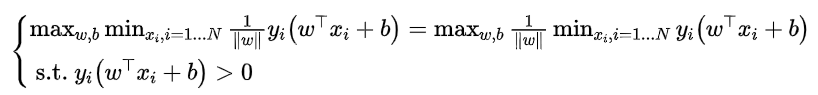
还可以提出这样的思想，

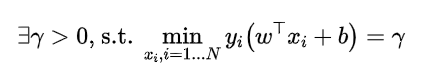
当γ=1时，就可以将之前的式子变化为：

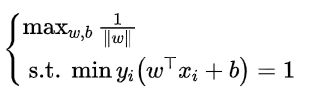
还可以将其中的约束条件由等式条件变换为不等式条件：

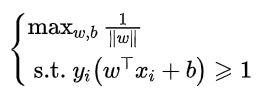
进一步化简可以得到：

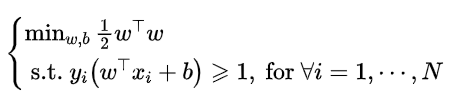
这样，便可以得到二次的最优化模型，其中包含有N个约束，这是一个凸优化模型——带约束的优化问题

模型求解

将上述的二次最优化模型的约束条件稍加变化边可以调整为：

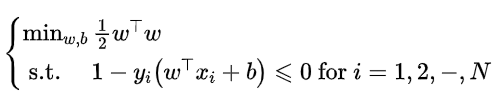
由此可以引入拉格朗日乘子，即：

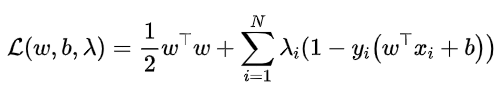
然后可以将带约束的最优化模型简化为无约束的最优化模型：

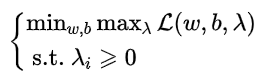
这样变化的原理是：
可以把(w,b)作为一个大集合，将其中分为两部分来讨论：


所以，

又因为该模型属于二次凸优化模型+线性约束，所以满足强对偶关系，进一步将模型转化为，

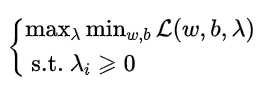
强对偶与弱对偶
弱对偶：

强对偶：

得到了对偶后的模型后，可以进一步简化，

于是可以得到模型：

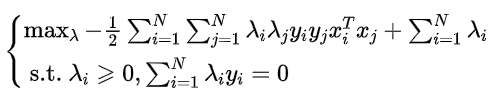
也可以将其转化为最小化来表达：

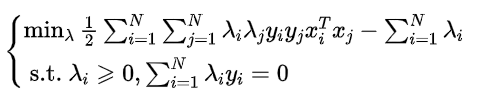
KKT条件

由于原题对偶情况下满足强对偶关系的充要条件是满足KKT条件，即

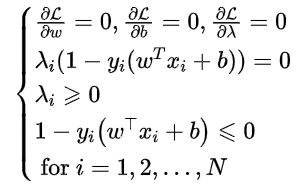
所以可以容易得到：w，即

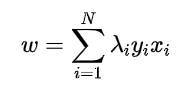
结合图，利用KKT条件的第一条可以知道，除了处于margin线上的点，其它的点所对应的λi=0，

于是，可以用KKT条件的第三条求解得到：b，即

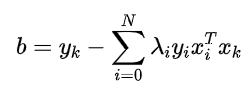
b的求解过程：

软间隔SVM

• 在实际问题中，有些数据是不可分的，或者有些数据是可分但存在一些噪声的，所以引入软间隔SVM来允许一些些错误（增加一些容错率）
  所以可以先假设对目标函数进行改写：
  原最优化模型为：
  
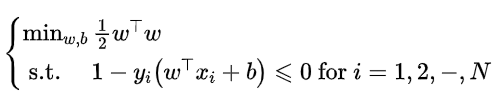
  可以将其目标函数改为：
  
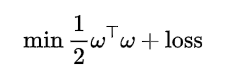
  其中loss是那个容错率，它有两种选择方案：

1. loss表示允许出现错误的点的个数：
   于是，可以将loss定义为：
   
   其中：
   
   但是，这样得到的loss是不连续的，所以通常不采取这样的形式

2. loss表示允许出现错误的距离：
   
   所以，
   

于是，可以得到新的最优化模型：

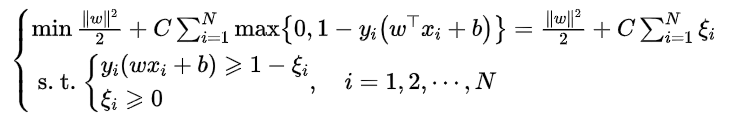
而它的解的形式与硬件隔SVM解的形式是相同的，其系数w和b也是相同的，即


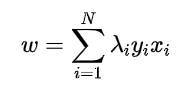
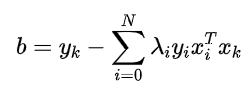
只不过：

libsvm软件包

参考链接

https://www.csie.ntu.edu.tw/~cjlin/libsvm/

SVM训练函数svmtrain

• 函数svmtrain用于创建一个SVM模型，其调用格式为：
  model=svmtrain(train_label,train_matrix,'libsvm_options');

• model：训练好的SVM模型
• train_model：训练集样本对应的类别标签
• train_matrix：训练集样本的输入矩阵
• libsvm_options：
  -s svm类型：SVM设置类型（默认0)
  　　　　0 — C-SVC； 1 –v-SVC； 2 – 一类SVM； 3 — e-SVR； 4 — v-SVR
  -t 核函数类型：核函数设置类型（默认2）
  　　　　0 – 线性核函数：u’v
  　　　　1 – 多项式核函数：（ru’v + coef0)^degree
  　　　　2 – RBF(径向基)核函数：exp(-r|u-v|^2）
  　　　　3 – sigmoid核函数：tanh(ru’v + coef0)
  -d degree：核函数中的degree设置（针对多项式核函数）（默认3）
  -g gamma：核函数中的gamma函数设置（针对多项式/rbf/sigmoid核函数）（默认1/k，k为总类别数)
  -r coef0：核函数中的coef0设置（针对多项式/sigmoid核函数）（（默认0)
  -c cost：设置C-SVC，e -SVR和v-SVR的参数（损失函数）（默认1）
  -n nu：设置v-SVC，一类SVM和v- SVR的参数（默认0.5）
  -p p：设置e -SVR 中损失函数p的值（默认0.1）
  -m cachesize：设置cache内存大小，以MB为单位（默认40）
  -e eps：设置允许的终止判据（默认0.001）
  -h shrinking：是否使用启发式，0或1（默认1）
  -wi weight：设置第几类的参数C为weight*C (C-SVC中的C) （默认1）
  -v n: n-fold交互检验模式，n为fold的个数，必须大于等于2
  以上这些参数设置可以按照SVM的类型和核函数所支持的参数进行任意组合，
  如果设置的参数在函数或SVM类型中没有也不会产生影响，程序不会接受该参数；如果应有的参数设置不正确，参数将采用默认值。

SVM预测函数svmpredict

• 函数svmpredict用于利用已经建立的SVM模型进行仿真预测，其调用格式为：
  [predict_label,accuracy/mse,decision_values/prob_estimates]=svmpredict(test_label,test_matrix,model);

• predict_label：预测得到的测试集样本的类别标签
• accuracy/mse：测试集的分类准确率，如果未提供正确值时，此参数便不再需要考虑;回归的均方根误差、回归的平方相关系数，对于回归问题要关注的是后面的参数
• decision_values/prob_estimates：一个矩阵包含决策的值或者概率估计。对于n个预测样本、k类的问题，如果指定“-b 1”参数，则n x k的矩阵，每一行表示这个样本分别属于每一个类别的概率；如果没有指定“-b 1”参数，则为n x k*(k-1)/2的矩阵，每一行表示k(k-1)/2个二分类SVM的预测结果。
• test_label：测试集样本对应的类别标签
• test_matrix：测试集样本的输入矩阵
• model：已经训练好的SVM模型

MATLAB程序

对于分类&回归，SVM的算法流程基本一致：

1. 产生训练集/测试集/实验集（需要分类与预测的数据集）
2. 数据归一化
3. 对训练集进行训练来创建SVM模型
4. 对测试集进行SVM仿真测试
5. 对实验集进行SVM分类与预测

• 对于回归（预测）问题，有两种类型：
  a. 对于基于对象属性的预测问题，提供的训练集的每个元素是一个向量，每个元素对应一个数值，则这种情况时可以在得到SVM模型后，通过输入一个向量元素作为对象的属性，来获得预测值
  b. 对于长时间的未来预测问题，提供的训练集的每个元素是时间t，每个时间对应一个数值，则这种情况时可以在得到SVM模型后，通过输入未来的时间，来获得未来该对象的变化情况

分类

回归（预测）