impulse 함수 - Yunjong-Lee/WiKi GitHub Wiki

date: 2024-12-01 19:27:17 layout: post

임펄스 신호는 아주 짧은 시간에 아주 큰 에너지를 가지는 신호(예를 들면, 번개와 같은...)를 말한다.
임펄스 신호와 같이, 아주 짧은 시간에 아주 큰 에너지를 가지는 함수를 임펄스 함수라고 한다.
임펄스 함수는 델타($\delta$) 함수 또는 dirac delta 함수라고도 불린다.
그리고, 임펄스 함수가 입력되었을 때 시스템에 의해서 나타나는 출력을 임펄스 응답이라고 한다.

정의

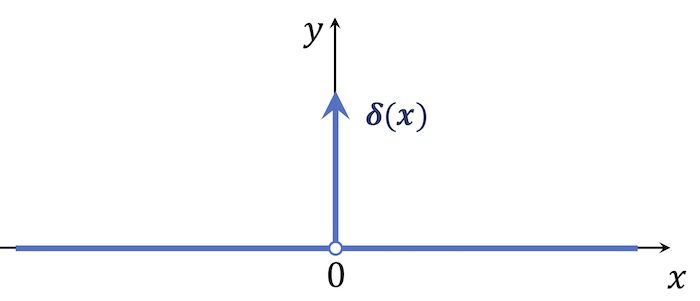
$x = 0$에서 크기가 무한대이고 $x ≠ 0$에서 크기가 0안 험수, 또한 모든 영역(−∞ ~ ∞)에 대해 적분하면, 1로 정의되는 특이한 함수
- $\delta(x) = 0, ... if, x ≠ 0$, --- 식(1)
  $ = ∞, ... if, x = 0$
- $\int ^{∞} _{−∞} \delta(x) dx = 1$

댈터 험수의 성질

델타 함수 $\delta(x)$에 어떤 임의의 함수 $f(x)$를 곱한 것은 $\delta(x)$에 $f(0)$를 곱한 것과 같다.
- $f(x)δ(x)=f(0)δ(x)$ --- 식 (1-2)
  - 이유: 델타 함수는 $x ≠ 0$일 때는 값이 0이고, $x = 0$일 때만 값이 존재하기 때문.
- 또, $\int ^{∞} _{−∞} f(x) \delta(x) dx = f(0) \int ^{∞} _{−∞} \delta(x) dx = f(0)$ --- 식(1-3)
  - 여기서 $f(0)$는 $x = 0$에서 함수 값으로써 상수이므로 적분 밖으로 이동될 수 있다.
  - 이 식은 델타 함수와 어떤 함수의 곲을 음의 무한대부터 양의 무한대까지 적분하면 $x = 0$에서의 함수 값을 구할 수 있다는 뜻임.
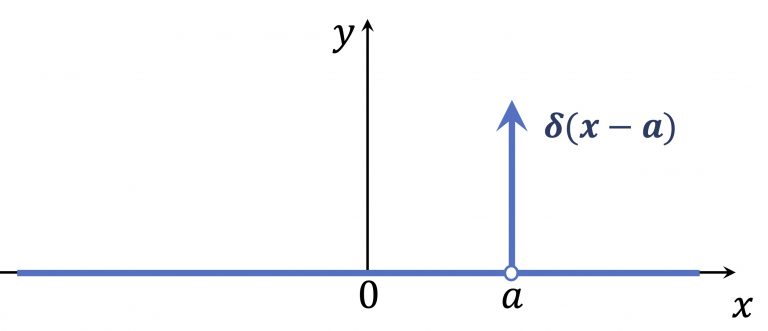
델타 함수 $δ(x)$를 $a$ 평행이동하면 $δ(x−a)$가 된다. 식 (1)의 $x$를 $x−a$ 바꾸어주면 식(2)가 성립된다.
- $\delta(x-a) = 0, ... if, x ≠ 0$, --- 식(2)
  $ = ∞, ... if, x = 0$
- (1-2), (1-3)식의 성질을 평행이동한 델타함수에 그대로 적용하면 다음의 관계도 성립한다.
  - $f(x)δ(x−a) = f(a)δ(x−a)$ --- 식 (2-2)
  - $\inf ^{∞} _{-∞} f(x)δ(x−a)dx = f(a) \inf ^{∞} _{-∞} δ(x−a)dx=f(a)$ --- 식 (2-3)
  - 델타함수는 우함수(y축 대칭) : $δ(x)= δ(−x)$ --- 식 (2-4)
  - $δ(ax) = \frac{1}{|a|} δ(x)$ --- 식(2-5)

$\int ^{t_2} _{t_1} x(t) \delta(t) dt = x(0)$, $t_1 < 0 < t_2 $