Heaps - YashasKamath/IECSE-Summer-Bootcamp-2022 GitHub Wiki

A heap is a tree-based data structure in which a special relationship exists between each parent and child node pair.

We will be dealing with only binary heaps(henceforth, all heap refers to binary heap) over our summer project. A binary heap can be defined as a binary tree with keys assigned to its nodes, one per node, provided the following two conditions are met:

1. The Shape Property - the binary tree is complete , i.e., all its levels are full except possibly the last level, where only some rightmost leaves may be missing.
2. The heap property - the key in each node follows a special relationship with the keys in its children: key_parent >= each key_child (a max heap) or key_parent <= each key_child (a min heap).

Consider the 3 trees depicted below:

The leftmost tree is a heap(max heap) as it satisfies both the shape as well as the heap properties. The middle tree is not a heap as it violates the shape property(node with key 5 has no left child). The rightmost tree is not a heap as it violates the heap property(there is no special relation which is consistent across all parent child node pairs).

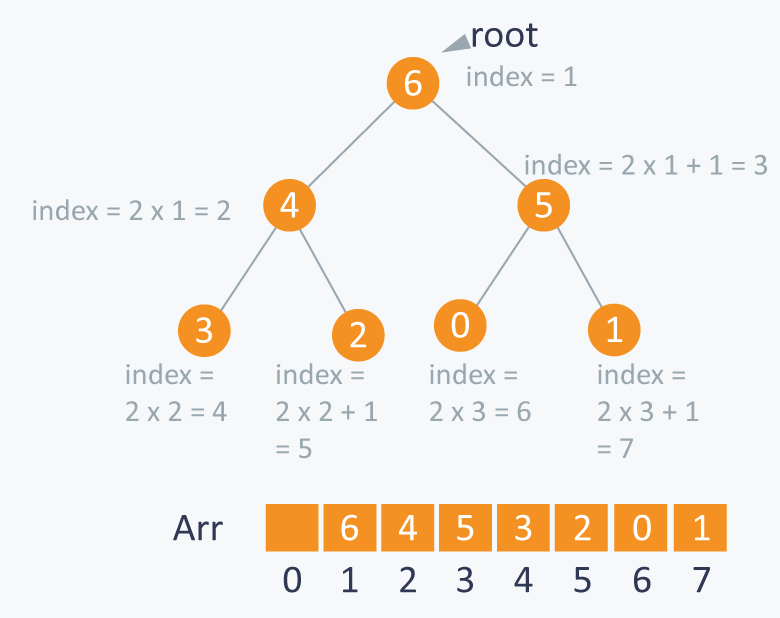
The fact that a heap is always a complete binary tree can be exploited to store it easily: An array can be used to simulate a binary tree in the following way. If we are storing one element at index i in array Arr, then its parent will be stored at index [i/2] (unless its a root, as root has no parent) and can be accessed by Arr[i/2] , its left child can be accessed by Arr[2*i] and its right child can be accessed by Arr[2*i+1]. Index of root will be 1 in an array (1-based indexing).

As the heap is a complete binary tree ensures that there are no missing middle elements in our tree-array, i.e., the tree-array is completely filled from index 1,2,3...n, where n is the number of elements in the heap.

When talking about Heaps, we consider 2 main kinds:

1. Min Heap : In this the value of the key of each parental node is less than all of it's children nodes.
2. Max Heap : In this the value of the key of each parental node is greater than all of it's children nodes.

We will discuss Max Heap in detail. After this discussion, Min heap should be intuitive.

First, let us see how to build a heap out of a given array of n elements. For this we will first need to understand the heapify procedure.

Let’s assume that we have a heap having some elements which are stored in array Arr. Suppose we want to check and correct that if at a particular index as parent, the heap property is maintained, we can use the heapify procedure. In other words, we want to heapify the subtree rooted at a particular index.

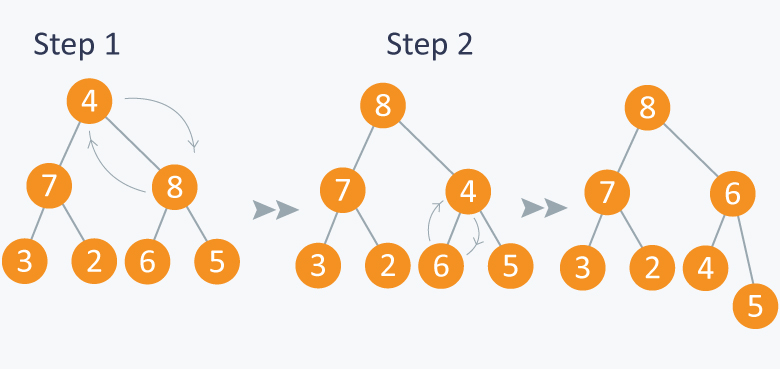
In the heapify process, we compare the key value of the node with the keys in it's child nodes. If the key of the node is not greater than all its children(possibly none), i.e., it violates the max-heap property, we swap the value at the index with the child having maximum key. But that is not enough, this swapped node may cause violations of max-heap property further down the tree. So we will recursively heapify the swapped node until no more violations occur.

The heapify procedure at a particular index can be applied only if both the left and the right child subtrees of that index have been heapified.

The following algorithm demonstrates the process:

ALGORITHM MaxHeapify(Arr[1..N], idx)
// Heapifies the subtree rooted at given index(idx), assuming that both the left
// and right subtrees of the given subtrees are perfect max heaps.
// Input: An array Arr[1..N] representing a heap of size N and
// the index idx at which we need to heapify.
// Output: We modify Arr[1..N] so that it represents the max heap.

leftchild ← 2 * idx       //left child
rightchild ← 2 * idx + 1  //right child
largest ← idx             //largest will store the index of largest key among parent, left and right child.
if leftchild <= N and Arr[leftchild] > Arr[largest] then
    largest ← leftchild
if rightchild <= N and Arr[rightchild] > Arr[largest] then
    largest ← rightchild
if largest != idx then 
    swap the values at Arr[idx] and Arr[largest]
    MaxHeapify(Arr[1..N],largest)  //recursively calling MaxHeapify for subtree rooted at swapped node

Time Complexity: The time complexity of the Heapification algorithm is O(log n). This is because, the maximum number of swap operations done depends on the height of the tree, and as a heap is always balanced, its height is always of the order of log n. The worst case scenario is that we are heapifying the index 1(root) of tree-array, and the key is such that it needs to be moved down to one of the leaf nodes (so it travels the entire height of the tree).

See the below illustration for better understanding of the heapification procedure. We call the heapification at the root node.

Now that we have studied heapify, we are well equipped to build our max heap from a given array of elements. We will assume that the given array is already a max-heap, and then proceed to modify it using heapify. Quite simply, we will heapify the subtrees rooted at all indexes, starting from the rightmost leaf(last index). This bottom-up approach is used, because heapifying a subtree rooted at index i only works when both of its left and right subtrees have already been heapified.

ALGORITHM BuildMaxHeap(H[1..n])
//Constructs a heap from elements of a given array
//Input: An array H [1..n]
//Output: A heap H [1..n] 
    for i=n to i=1:
        MaxHeapify(H[1..n], i)
    end for

What could be a simple optimization? We observe, a subtree of only one element is heapified by default - leaf nodes don't neeed to be heapified. So the idea is to find the position of the last non-leaf node and perform the heapify operation on each non-leaf node in reverse array-index order. Try to find this position yourself.

The application of the algorithm on the list [2,9,7,6,5,8] is illustrated below. As you can see, we start from the last non-leaf node, which is 7(index 3).

Time Complexity: Heapify is of the complexity log(n), and we use it for all the elements so, it might intuitively seem that the upper bound is O(nlog(n)). But, also observe the height of the subtree for every heapify operation keeps changing- it increases as we travel up the tree. It is possible to prove a tighter upper bound. In reality, for a list of n elements, the complexity of constructing a heap out of it will be O(n) only. You can find more information here.

To insert a new key K into a heap, we first attach a new node with key K in it after the last leaf of the existing heap (hence we increase the size of our tree-array by 1), then shift K up to its appropriate place in the new heap as follows:

Compare K with its parent’s key: if the latter is greater than or equal to K, stop (the structure is a heap); otherwise, swap these two keys and compare K with its new parent. This swapping continues until K is not greater than its last parent or it reaches the root. Time complexity is O(log n)- number of swaps depends on the tree height in worst case. See the below illustration of this process as we insert a key 10 into a heap with elements [9,6,8,2,5,7].

This is probably the most useful feature of a heap. For a max heap, we can access the maximum element in constant time(O(1)), because it will always be present at the root.

To delete the root or maximum element from a max heap, we swap the root with the last leaf node of the heap. Then we decrease the size of the heap by 1 to delete the element. Then to correct the possible violations in the modified heap, we call the heapify process on the root node (index = 1). The time complexity is O(log n).

We illustrate the process by deleting the maximum value from a heap with elements [9,8,6,2,5,1] below.

Left as an exercise.

• Link 1
• Link 2
• Link 3
• Link 4