Binary Tree - YashasKamath/IECSE-Summer-Bootcamp-2022 GitHub Wiki

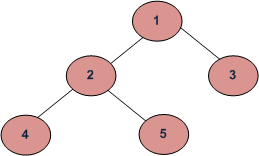
A binary tree is a tree in which each node has maximum 2 children. Since each element in a binary tree can have only 2 children, we typically name them the left and right child. It can be visualised as an upside down tree with a root node. The topmost node in the tree is called the root node. In the given example 2 is the root node.

Here's some terminologies used in trees:

1. Root – The top node in a tree.
2. Child – The just next nodes connected downwards.
3. Parent – The converse notion of child.
4. Siblings – Nodes with the same parent.
5. Descendant – a node reachable by repeated proceeding from parent to child.
6. Ancestor – a node reachable by repeated proceeding from child to parent.
7. Leaf – a node with no children.
8. Internal node – a node with at least one child.
9. External node – a node with no children.

To understand the structure of a tree, you need to understand the structure of a node of the tree, since a tree is just a collection of nodes where each node can point to maximum 2 elements.

struct Node
{
    int data;
    Node* left;
    Node* right;
};

As you can see, the structure is quite similar to that of a node in a linked list. The only difference is instead of pointing to one element, it can point to two elements. Taking the previous example, the node with data = 2, has it's left pointer pointing to node with data = 7 and right pointer to node with data = 5. Similarly node with data = 9 has it's left pointer pointing to node with data = 4 and right pointer points to null. From this you can easily deduce that leaf nodes have both the pointers set to NULL.

We'll be dealing with the node representation mostly, but the array representation is also used sometimes.
If the root of the tree is located at index 0, left child is represented by the index 2*i + 1, and right child is represented by index 2*i + 2.
If the root of the tree is located at index 1, left child will be at index 2*i and right child at index 2*i + 1.
You can use -1 to represent NULL nodes.
{1, 2, -1} represents a tree whose root is 1, left child of root is 2, and the right child is NULL.

The following function asks the user for directions to insert to the tree.

node* insert(node* root, int data)
{
    node* temp = createnode(data);
    node* temp2 = root;
    if(root == NULL)
    {
        return temp;
    }
    int choice;
    while(1)
    {
        printf("Current node is %d\nEnter your choice\n1. Left\n2. Right\n", temp2->data);
        scanf("%d", &choice);
        printf("%d\n", choice);
        if(choice == 1)
        {
            if(temp2->left != NULL)
                temp2 = temp2->left;
            else
            {
                temp2->left = temp;
                printf("Inserted to the left child of %d\n", temp2->data);
                break;
            }
        }
        else if(choice == 2)
        {
            if(temp2->right != NULL)
                temp2 = temp2->right;
            else
            {
                temp2->right = temp;
                printf("Inserted to the right child of %d\n", temp2->data);
                break;
            }
        }
        else
        {
            printf("Invalid\n");
        }
    }
    return root;
}

Creation of node here is similar to creating a node in Linked List. Choice = 1 signifies that user wants to add a left child and choice = 2 signifies user wants to add a right child. This is a basic creation function. Try to use the previous example and trace how will we insert a node 10 as the left child of node 5.

Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways.

1. Inorder (Left, Root, Right) : 4 2 5 1 3
2. Preorder (Root, Left, Right) : 1 2 4 5 3
3. Postorder (Left, Right, Root) : 4 5 2 3 1

Algorithms for each of the Traversals:

1. Inorder:

Step 1: Traverse the left subtree, i.e., call Inorder(left-subtree)
Step 2: Visit the root.
Step 3: Traverse the right subtree, i.e., call Inorder(right-subtree)

2. Preorder:

Step 1: Visit the root.
Step 2: Traverse the left subtree, i.e., call Preorder(left-subtree)
Step 3: Traverse the right subtree, i.e., call Preorder(right-subtree)

3. Postorder:

Step 1: Traverse the left subtree, i.e., call Postorder(left-subtree)
Step 2: Traverse the right subtree, i.e., call Postorder(right-subtree)
Step 3: Visit the root.

Function for Inorder Traversal is given below. It is easy to deduce the functions for Preorder and Postorder Traversals from the same.

void inorder(node* root)
{
    if(root == NULL)
        return;
    inorder(root->left);
    printf("%d ", root->data);
    inorder(root->right);
}

Level Order Tree Traversal: 1 2 3 4 5

This is a recursive algorithm that processes the root, followed by the children of the root (from left to right), followed by the grandchildren of the root (from left to right) and so on. This kind of traversal in general is known as Breadth First Traversal. This is usually implemented using queue.

Function for Level Order Tree Traversal is given below:

void levelOrder(Node * root) {
        queue<Node *> q;
        q.push(root);
        while(!q.empty())
        {
            cout<<q.front()->data<<" ";
            if(q.front()->left != NULL)
            {
                q.push(q.front()->left);
            }
            if(q.front()->right != NULL)
                q.push(q.front()->right);
            q.pop();
        }
    }