2 Social Plus Part - YMonnier/AdvAlgoLP GitHub Wiki
Social Plus - Family party
Your beloved aunt Petunia is throwing her namesday party, to which as usual, she invites all the family. There are however some animosities in the family. Aunt's idea is to have two separate tables for quest during the party, so that no two disliking one another pair of people will sit at the same table.
- Given the list of invited guests and a list of your aunt's suggestions on "who doesn't like whom",
- your task, as your aunt's dear little sausage computer genius, is to set up a "sitting scheme". Using DFS algorithm is a part of task requirement
- Make sure you are using a nonrecursive solution.
Summary
Execution
To execute the sitting table:
git clone [email protected]:YMonnier/AdvAlgoLP.gitcd AdvAlgoLP/Assignment2/SocialPlus- manage your graph into the
SeatingPlan.py python SeatingPlan.py
Implementation
We have a list of invited guest:
- Michel
- Vero
- Yann
- Jose
- Georges
- Peter
and a list of "who doesn't like whom":
| Guest | Dislike |
|---|---|
| Michel | Vero |
| Vero | Michel |
| Georges | Vero, Yann |
| Jose | Georges |
| Peter | Michel |
| Yann | Peter |
Below a directed graph which represents all data.
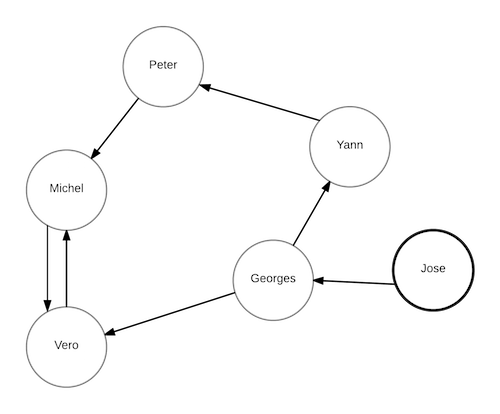
We apply for instance, Depth First Search Algorithm on the graph. We will start with the 'Jose' node. By applying the DFS algorimth, we will make a pi table(predecessor), for example we have node A, B and edge A-->B, the pi table means A is the predecessor of B so A dislike B.
When we want to assign a guest to a table, we check if his predecessor is not on a table.
Python
# Table of table (Table1, Table2, GetOut)
tables = ([], [], [])
# pi table (list of predecessor)
pi = {n:[] for n in graph}
# Depth First Algorithm for each node,
for person in graph: # because, some nodes can be not connected
if not graph[person].visited:
stack = []
stack.append(person)
pi[person].append(person)
while stack != []:
dislike_p = stack.pop()
if not graph[dislike_p].visited:
graph[dislike_p].visited = True
add_person(dislike_p, pi[dislike_p], tables)
for n in graph[dislike_p].neighbors:
pi[n.name].append(dislike_p)
stack.append(n.name)