2 Premium Part - YMonnier/AdvAlgoLP GitHub Wiki
Premium Part - "In the Labyrinth He Dwells"
In the TT tasks assume that corridors may have different positive lengths, which are given in the labyrinth map. The evil Lord Waldemar haunts the labyrinth. As one of his evil disciples your task is to find whether it is possible to block one corridor of the labyrinth so that a wizard can be kept from reaching the exit.
Summary
Execution
To execute the sitting table:
git clone [email protected]:YMonnier/AdvAlgoLP.gitcd AdvAlgoLP/Assignment2/Premium- manage your graph into the
Supervisor.py python Supervisor.py
Implementation
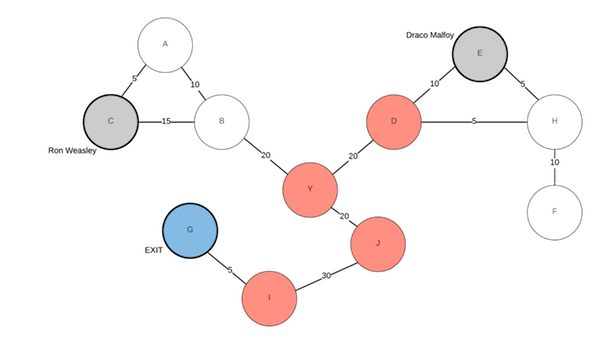
We have this graph(labyrinth)
- Wizard Ron Weasley: C
- Wizard Draco Malfoy: E
- Exit node: G
Now the graph has corridors with different positive distance. So we have to apply Dijkstra algorithm for wizards to find the shortest distance to reach the exit.
def dijkstra(graph, start, target):
start.distance = 0
#queue = [v for v in graph]
queue = [(graph[v].distance, v) for v in graph]
heapq.heapify(queue)
#heapq.heapify(queue)
while len(queue):
v = heapq.heappop(queue)
current = graph[v[1]]
current.visited = True
for n in current.neighbors:
if n.visited: # if visited, skip
continue
new_dist = current.distance + current.get_weight(n)
if new_dist < n.distance:
n.distance = new_dist
n.previous = current
# Rebuild the queue with unvisited nodes
queue = [(graph[v].distance, v) for v in graph if not graph[v].visited]
heapq.heapify(queue)
To make the Evil plan, we need to find the bridges on the graph. For that, we will use DFS.
'''
Apply DFS to find bridges on the current graph
@param u, previous node
@param v, node we want to visite
@param pre, order in which dfs examines v (discovery times of visited vertices)
@param low, lowest preorder
@param count, discovery time
@param res, list of bridges discovered(tuple from,to)
'''
def dfs(u, v, pre, low, count, res): # Apply DFS to find bridges
count += 1
pre[v] = count
low[v] = pre[v]
for n in self.graph[v].neighbors:
if pre[n.name] == -1:
dfs(v, n.name, pre, low, count, res)
low[v] = min(low[v], low[n.name])
if low[n.name] == pre[n.name]:
res.append((v, n.name))
elif n.name != u:
low[v] = min(low[v], pre[n.name])
Then we will apply the BFS algorithm for each bridges's way to find in which way is the exit and wizards. If exit and wizard are are in a different side, it means that the evil can block wizard by this bridge.
For the proviso graph, the evil can block
- Ron Weasley at position Y
- Draco Malfoy at position D
- Ron Weasley and Draco Malfoy at position I and J