1 Social Part - YMonnier/AdvAlgoLP GitHub Wiki
Social Part - "Mom got me a new computer"
Implement the following pattern matching algorithms: Brute-force, Sunday, a version of KMP, a version of FSM, a version of Rabin-Karp. Compare their all runing times on a chapter of a book, with small and large pattern.
Real Time: Calculation execution time of algorimth (including time used by other programs) so it will seem to take more time when your computer is busy doing other stuff.
All tests were done from this online book: The Adventure of the Speckled Band
If you want to search a word with specific length into a file, execute this command:
grep -o -w '\w\{length\}' file.txt.
Example:
- content of book.txt: "The Aduenture of the Speckled Band"
grep -o -w '\w\{4\}' book.txtreturnBand
References:
- Introduction to Algorithms, Third Edition By Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein
- Strings and Pattern Matching
- Stackoverflow
Summary
Execution
To execute all algorithms:
git clone [email protected]:YMonnier/AdvAlgoLP.gitcd AdvAlgoLP/Assignment1/Social- change text and pattern into
main.py(sandpatternvariable) python main.py
Output:
==> Pattern :: unapproachable
==> Pattern Length :: 14
*************************************************
************* Brute Force Algorithm *************
*************************************************
==> Execution time: 0.00969910621643 seconds
==> 1 matchings
**************************************************
**************** Sunday Algorithm ****************
**************************************************
==> Execution time: 0.0243558883667 seconds
==> 1 matchings
*************************************************
***************** KMP Algorithm *****************
*************************************************
==> Execution time: 0.010568857193 seconds
==> 1 matchings
*************************************************
***************** FSM Algorithm *****************
*************************************************
==> Execution time: 0.0167770385742 seconds
==> 1 matchings
*************************************************
************* Rabin-Karp Algorithm **************
*************************************************
==> Execution time: 0.0702619552612 seconds
==> 1 matchings
Brute-Force Search Matching
The principles of brute force string matching are quite simple. Brute-Force Algorithm match the string character by character (Text) until matched (Pattern)
- Doesn’t require pre-processing of the text.
- Usefull for short texts and patterns.
- Worst case time complexity O(n.m), n = length of the text and m length of the pattern.
- Best case time complexity if pattern found: Ο(m), m length of the pattern.
- Best case time complexity if pattern not found: Ο(n), n length of the text.
Text = "ABDAAAHDF"
Pattern = "AAAH"
1- ABDAAAHDF |
AAAH | unmatched
2- ABDAAAHDF |
AAAH | unmatched
3- ABDAAAHDF |
AAAH | unmatched
4- ABDAAAHDF |
AAAH | MATCHED
Implementation
Python
"""
T: The search area
P: The candidate to do the search
"""
def bruteForce(T, P):
# Text length
n = len(T)
# Pattern length
m = len(P)
# Index of occurrences found
shifts = []
for i in xrange(0, n - (m-1)):
j = 0
while j < m and T[i + j] == P[j]:
j = j + 1
if j == m:
shifts.append(i)
return shifts
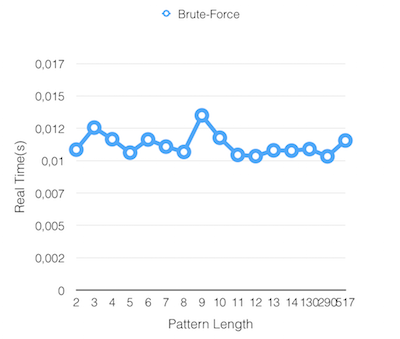
Results
Sunday Search Matching
The special feature of Sunday Algorithm is on preprocessing. Creation of array which, for each symbol of the alphabet, stores the position of its rightmost occurrence in the pattern.
- Algorithm performs just O(n/m) comparisons
Text = "bamamaababa"
Pattern = "mama"
# Preprocessing
occ = ['a' = 3,
b = -1,
c = -1,
d = -1,
...,
l = -1,
m = 2,
n = -1,
o = -1
,... next alphabet]
# Algorithm
1.
1
01234567890
bamamaababa
mama | i = 0, check if mama match. Unmatched, i = i + length(Pattern)
| i = 4
| i < length(Text): i = i - occ[i] (m: 2)
2.
1
01234567890
bamamaababa
mama | i = 2, check if mama match. MATCHED! i = i + length(Pattern)
| i = 6
| i < length(Text): i = i - occ[i] (a: 3)
3.
1
01234567890
bamamaababa
mama | i = 3, check if mama match. Unmatched! i = i + length(Pattern)
| i = 7
| i < length(Text): i = i - occ[i] (b: -1)
4.
1
01234567890
bamamaababa
mama | i = 8, check if mama match. Unmatched!
Implementation
Python
'''
Preprocessing sunday
@param P: Text
'''
def preprocessing(P):
m = len(P)
occ = {}
alphabet = string.ascii_letters + string.punctuation + string.digits + string.whitespace
# each character of the alphabet
for char in alphabet:
occ[char] = -1
# Store for each patter's character the rightmost index
for i in range(m):
char = P[i]
occ[char] = i
return occ
'''
Check pattern matches with text at specific index
@param T: Text
@param P: Pattern
@param i: Index from text
'''
def isInP(T, P, i):
for char in P:
if char != T[i]:
return False
i += 1
return True
'''
Sunday Algorithm
@param T: The search area
@param P: The candidate to do the search
'''
def sunday(T, P):
#Preprocessing
occ = preprocessing(P)
i = 0
shifts = []
n = len(T)
m = len(P)
while(i < n):
if isInP(T, P, i):
shifts.append(i)
i += m
if i < n:
i -= occ[T[i]]
return shifts
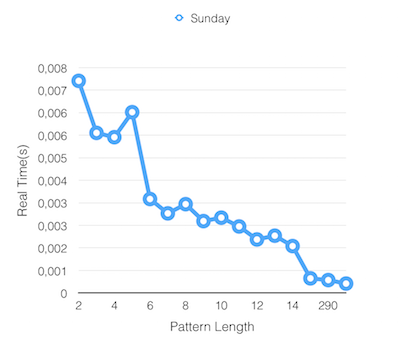
Results
Knuth-Morris-Pratt Search Matching
Knuth-Morris-Pratt Algorithm resides in a preprocessing chain, which provides enough information to determine where to continue to search for non-correspondance. This allow the algorithm to not re-examine the characters that were previously checked and therefore limit the number of necessary comparisons. The preprocessing build a automaton(single array) with different states. If, we go to the final state, it means that an occurence has been found.
Text = "ABRA ABRACAD ABRACADABRA"
Pattern = "ABRACADABRA"
1-
1 2
j - 012345678901234567890123
t - ABRA ABRACAD ABRACADABRA
p - ABRACADABRA | unmatched
i - 01234567890
2-
1 2
j - 012345678901234567890123
t - ABRA ABRACAD ABRACADABRA
p - ABRACADABRA | unmatched
i - 01234567890
3-
1 2
j - 012345678901234567890123
t - ABRA ABRACAD ABRACADABRA
p - ABRACADABRA | MATCHED
i - 01234567890
Implementation
Python
'''
Table-building
@param P: The candidate to do the search
'''
def preprocessing(P):
m = len(P)
pi = [0] * m
k = 0
for q in range(1,m):
while k > 0 and P[k] != P[q]:
k = pi[k]
if P[k] == P[q]:
k = k + 1
pi[q] = k
return pi
'''
@param T: The search area
@param P: The candidate to do the search
'''
def KMP(T, P):
# Preprocessing
pi = preprocessing(P)
shifts = []
n = len(T)
m = len(P)
q = 0 # number of characters matched
for i in range(1, n): # scan the text from left to right
while q > 0 and T[i] != P[q]:
q = pi[q] # next character does not match
if T[i] == P[q]:
q += 1 # next character matches
if q == m: # is all of P matched
shifts.append(i - (m-1))
q = 0
return shifts
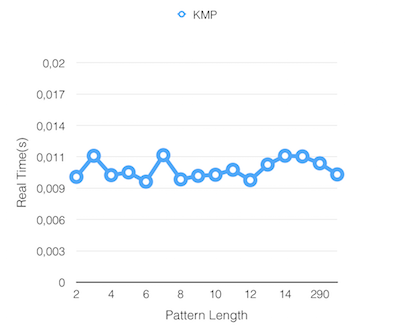
Results
Finite State Machine Search Matching
Finite State Machine search algorithm is almost the same method as KMP algorithm. Fro the pre-processing we use an two-dimensional array which represent the Finite Automata.
Implementation
Python
'''
Preprocessing
@param P: The candidate to do the search
'''
def computeTransition(P):
m = len(P)
alphabet = string.ascii_letters + string.punctuation + string.digits + string.whitespace
trans = [{c:0 for c in alphabet} for i in range(m)]
for q in range(m):
for c in alphabet:
k = min(m, q+1)
while P[:k] != (P[:q]+c)[-k:]:
k-=1
trans[q][c]=k
return trans
'''
Finite State Machine Algorithm
@param T: The search area
@param P: The candidate to do the search
'''
def FSM(T, P):
#Preprocessing
trans = computeTransition(P)
shifts = []
m = len(P)
n = len(T)
q = 0
for i in range(0, n):
q = trans[q][T[i]]
if q == m:
shifts.append(i-m+1)
q = 0
return shifts
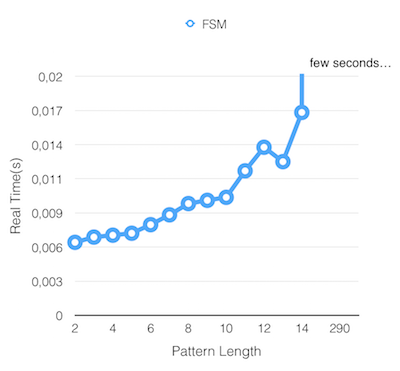
Results
Rabin-Karp Search Matching
The Rabin-Karp string searching algorithm uses a hash function to speed up the search.
- The Rabin-Karp string searching algorithm calculates a hash value for the pattern, and for each M-character subsequence of text to be compared.
- If the hash values are unequal, the algorithm will calculate the hash value for next M-character sequence.
- If the hash values are equal, the algorithm will do a Brute Force comparison between the pattern and the M-character sequence.
hash_p = hash value of pattern
hash_t = hash value of first M letters in body of text
Text = "ABDAAAHDF"
Pattern = "AAAH"
hash_p = 100 ('AAAH')
hash_t = 46 ('ABDA')
1- ABDAAAHDF |
AAAH | 46 != 100, unmatched
hash_t = 89 | hash value of next section of text, one character over ('BDAA')
2- ABDAAAHDF |
AAAH | 89 != 100, unmatched
hash_t = 76 | hash value of next section. ('DAAA')
3- ABDAAAHDF |
AAAH | 76 != 100, unmatched
hash_t = 100 | hash value of next section. ('AAAH')
3- ABDAAAHDF |
AAAH | 100 == 100, matched
Implementation
Pseudo Code
hash_p = hash value of pattern
hash_t = hash value of first M letters in body of text
do
if (hash_p == hash_t)
brute force comparison of pattern and selected section of text
hash_t = hash value of next section of text, one character over (rolling hash)
while (end of text or brute force comparison == true)
Python
'''
@param T: The search area
@param P: The candidate to do the search
'''
def rabinKarp(T, P):
n = len(T)
m = len(P)
d = 257
q = 11
h = pow(d,m-1)%q
hash_p = 0
hash_t = 0
shifts = []
for i in range(m): # preprocessing (hash)
hash_p = (d * hash_p + ord(P[i])) % q
hash_t = (d * hash_t + ord(T[i])) % q
for s in range(n - m + 1): # matching
if hash_p == hash_t: # if match
match = True
for i in range(m):
if P[i] != T[s + i]:
match = False
break
if match:
shifts.append(s)
if s < n-m: # substract first text letter hash and add last hash letter
hash_t = (hash_t - h * ord(T[s])) % q
hash_t = (hash_t * d + ord(T[s + m])) % q
hash_t = (hash_t + q) % q
return shifts
Results
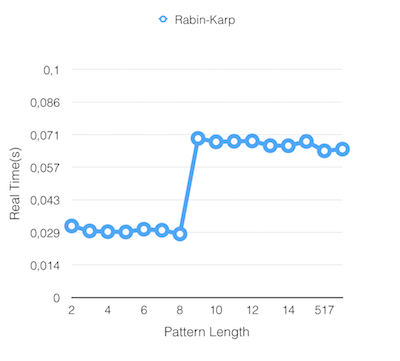
Conclusion
Realm-Time graph algorithms
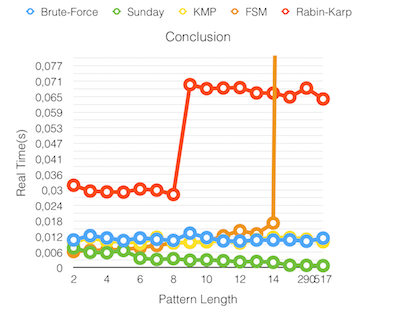
Table of pattern tested
| Patterns | Length | Matching |
|---|---|---|
| of | 2 | 293 |
| his | 3 | 150 |
| than | 4 | 15 |
| which | 5 | 95 |
| cannot | 6 | 8 |
| perhaps | 7 | 8 |
| terrible | 8 | 6 |
| whispered | 9 | 3 |
| ventilator | 10 | 15 |
| communicate | 11 | 3 |
| dark-lantern | 12 | 2 |
| investigation | 13 | 3 |
| unapproachable | 14 | 1 |
| para0.txt | 290 | 1 |
| para1.txt | 517 | 1 |
| para2.txt | 130 | 1 |