Описание свёрточной нейронной сети - ValeriaPlatonova/CNN GitHub Wiki
Свёрточная нейронная сеть
Сверточная нейронная сеть (СНС) — специальная архитектура нейронных сетей, нацеленная на эффективное распознавание образов.
Её задача — это приём начального изображения на вход и вывод его класса (кошка, собака и т.д.) или группы вероятных классов.
Входные данные – изображение. Изображение для компьютера, это массив пикселей. Если изображение черно-белое, то это просто массив интенсивностей, а если цветное, то массив векторов из трех чисел, обозначающих интенсивности трех основных цветов (красного, зеленого и черного в стандартном RGB). В зависимости от разрешения и размера изображения, размер массива может быть 32х32х3 (где глубина 3 — это значения каналов RGB). Например, цветное изображение в формате JPG, и его размер 480х480. Соответствующий массив будет 480х480х3. Каждому из этих чисел присваивается значение от 0 до 255, которое описывает интенсивность пикселя в этой точке. Эти цифры являются единственными входными данными, доступными компьютеру. Идея в том, что вы даете компьютеру эту матрицу, а он выводит числа, которые описывают вероятность класса изображения (.80 для кошки, .15 для собаки, .05 для птицы и т.д.).
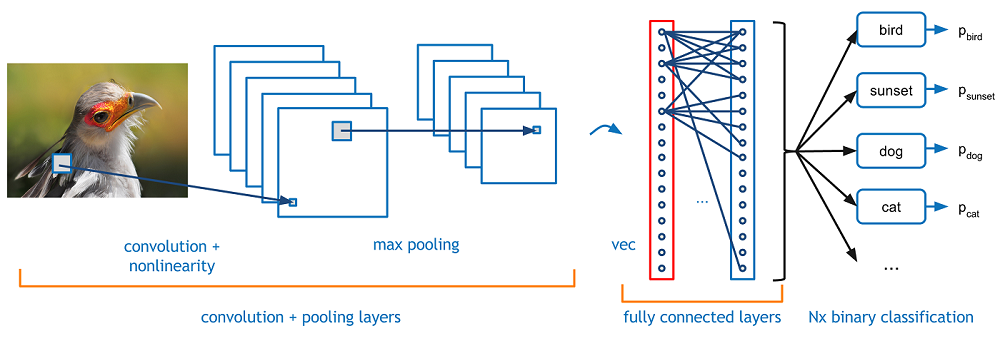
Общее описание работы
Нам нужно, чтобы компьютер мог различать изображения и распознавать уникальные особенности, которые делают собаку собакой, а кошку кошкой. Работа СНС в общем представлении, это переход от конкретных особенностей изображения к более абстрактным деталям, и далее к ещё более абстрактным деталям… до выделения понятий высокого уровня. При этом сеть самонастраивается и вырабатывает сама необходимую иерархию абстрактных признаков (последовательности карт признаков), фильтруя маловажные детали и выделяя существенное.
Если конкретнее, берётся изображение, пропускается через серию свёрточных (convolution layers), нелинейных слоев, слоев объединения и полносвязных слоёв, и генерируется вывод (класс или вероятность классов, которые лучше всего описывают изображение).
Что делает каждый слой
Первый слой всегда свёрточный. Входное изображение — это матрица с пиксельными значениями размером, например, 32х32х3. Свёрточный слой или фильтр (или нейрон, ядро) — это матрица размером, например, 5х5х3 (такую матрицу ещё называют матрицей весов или матрицей параметров). Глубина у этого фильтра должна быть такой же, как и глубина входного изображения. Свертка производится следующим образом — фильтр «скользит» по входным данным и умножает значения матрицы фильтра на исходные значения тех пикселей матрицы изображения (поэлементное умножение) над которыми в данный момент находится. В нашем примере получится 75 умножений, все эти умножения суммируются, в итоге получается одно число. Это число просто символизирует нахождение фильтра в верхнем левом углу изображения. Следующий шаг – перемещение фильтра вправо на единицу и так далее, процесс повторяется в каждой позиции. И каждая уникальная позиция исходного изображения производит число. После прохождения фильтра по всем позициям из матрицы 32х32 получается матрица 28х28, которую называют функцией активации или картой признаков. Получается матрица 28х28 т.к. при наложении фильтра 5х5 на изображение 32х32 может получится только 784 различных локации фильтра. Так происходит свертка.
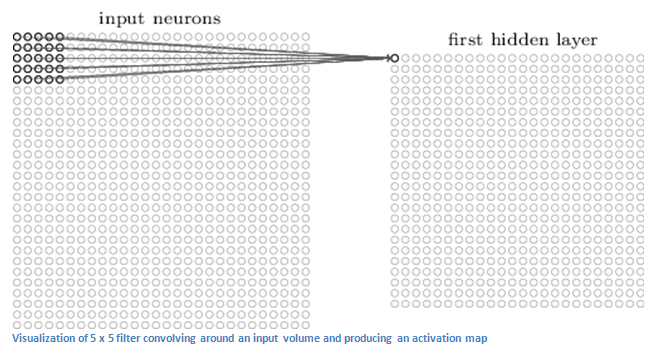
Про свертку подробнее. Первый слой
Каждый фильтр можно рассматривать как идентификатор свойства (прямые границы, простые цвета и кривые). Т.е. самые простые характеристики, которые имеют все изображения в общем. Например, фильтр 7х7х3, и он будет детектором кривых. Для простоты игнорируем глубину 3 и рассматриваем только верхний слой фильтра и изображения. У фильтра пиксельная структура, в которой вдоль области, определяющей форму кривой, численные значения выше.
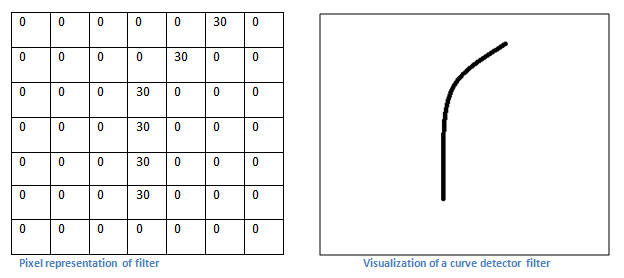
Возьмем пример изображения, которому надо присвоить класс и установим фильтр в верхнем левом углу:
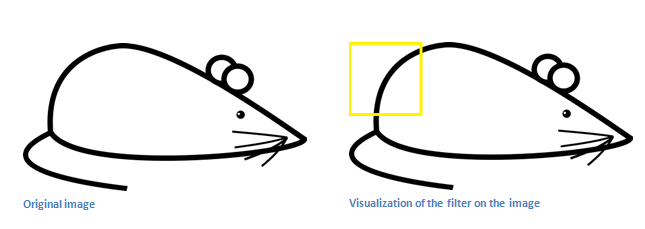
Значения фильтра умножаются на значения пикселей исходного изображения той области, на которую накладывается фильтр. Если на входном изображении есть форма, похожая на кривую фильтра и все умножения суммируются, то получится большое значение.
Теперь рассмотрим положение фильтра в другой области изображения. Значение будет сильно ниже потому, что в новой области изображения нет ничего, что мог засечь фильтр кривой.
Вывод свёрточного слоя — карта свойств. В нашем простом примере этот фильтр — детектор кривой, карта свойств покажет области, в которых больше вероятности наличия кривых. В левом верхнем углу значение нашей 28х28х1 карты свойств будет 6600, что показывает, что что-то похожее на кривую присутствует на изображении, и такая вероятность активировала фильтр. В правом верхнем углу значение у карты свойств будет 0, нет ничего, что могло активировать фильтр, т.е. кривой нет. Это только один фильтр. Могут быть другие фильтры для других типов линий. Чем больше фильтров, тем больше глубина карты свойств, и тем больше информации мы имеем о входном изображении.
На рисунке ниже видны примеры визуализаций фильтров первого свёрточного слоя обученной сети. Но идея здесь та же — фильтры на первом слое сворачиваются вокруг исходного изображения и "активируются" (или производят большие значения), когда специфическая черта, которую они ищут присутствует на изображении.
Глубже в сеть
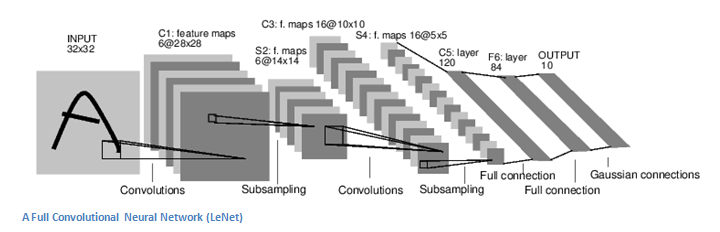
В классической архитектуре СНС применяются и другие слои, которые перемежаются со свёрточными. Классическая архитектура СНС выглядит так:
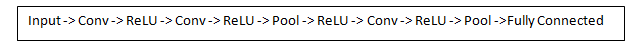
Фильтры первого свёрточного слоя детектируют свойства базового уровня, такие как границы и кривые. Чтобы предположить какой тип объекта изображён на изображении, нужна сеть, способная распознавать свойства более высокого уровня — руки, лапы, глаза, уши…
Выходной результат сети после первого свёрточного слоя в нашем примере выглядит следующим образом: его размер 28х28х3 (мы используем три фильтра 5х5х3). Когда картинка проходит через один свёрточный слой, выход 1-го слоя становится входным значением 2-го. Для 1-го слоя входом были только данные исходного изображения. Но при переходе ко 2-му слою, вводным значением для него станет одна или несколько карт свойств — результат обработки предыдущего слоя. Каждый набор входных данных описывает позиции, где на исходном изображении встречаются определенные базовые признаки.
Далее при прохождении через второй свёрточный слой на выходе будут активированы фильтры, которые представляют свойства более высокого уровня. Типами этих свойств могут быть комбинации прямой границы с изгибом или сочетание нескольких прямых. Чем больше свёрточных слоёв проходит изображение и чем дальше оно движется по сети, тем более сложные характеристики выводятся в картах активации. В конце сети могут быть фильтры, которые активируются при наличии рукописного текста на изображении, при наличии объектов определенных цветов и т.д. При движении вглубь сети, фильтры работают со все большим полем восприятия, и обрабатывают информацию с большей площади первоначального изображения.
Слой активации
Скалярный результат каждой свёртки попадает на функцию активации, которая представляет собой некую нелинейную функцию. Слой активации логически объединяют со слоем свёртки (считают, что функция активации встроена в слой свёртки). Функция нелинейности может быть любой по выбору исследователя. Наиболее часто используемыми функциями активации в глубоких нейросетях являются функция ReLu (rectified linear unit – блок линейной ректификации) и ее модификации. Данная функция позволяет оптимизировать процесс обучения и упрощает вычисления, т.е. по сути это операция отсечения отрицательной части скалярной величины.
Пулинг или слой субдискретизации (pooling layers, subsampling layers)
Слой пулинга (подвыборки, субдискретизации) представляет собой нелинейное уплотнение карты признаков, при этом группа пикселей (обычно размера 2х2) уплотняется до одного пикселя, проходя нелинейное преобразование. Наиболее употребляемая, при этом, функция максимума (max pooling). Преобразования затрагивают непересекающиеся прямоугольники или квадраты, каждый из которых cжимается в один пиксель, при этом выбирается пиксель, имеющий максимальное значение. Операция пулинга позволяет существенно уменьшить пространственный объем изображения. Пулинг интерпретируется так: если на предыдущей операции свёртки уже были выявлены некоторые признаки, то для дальнейшей обработки настолько подробное изображение уже не нужно, и оно уплотняется до менее подробного. Слой пулинга, как правило, вставляется после слоя свёртки перед слоем следующей свёртки.
Полносвязные слои (fully connected layers)
После нескольких итераций свёртки изображения и уплотнения с помощью пулинга система перестраивается от конкретной сетки пикселей с высоким разрешением к более абстрактным картам признаков, на каждом следующем слое увеличивается число каналов и уменьшается размерность изображения в каждом канале. В итоге, остаётся большой набор каналов, хранящих небольшое число данных, которые интерпретируются как самые абстрактные понятия, выявленные из исходного изображения. Эти данные объединяются и передаются на полносвязную нейронную сеть, которая тоже может состоять из нескольких слоёв. При этом полносвязные слои уже утрачивают пространственную структуру пикселей и обладают сравнительно небольшой размерностью (по отношению к количеству пикселей исходного изображения).
Полносвязный слой берёт входные данные и выводит N-пространственный вектор, где N — число классов, из которых программа выбирает нужный. Например, при распознавании цифр, у N будет значение 10, потому что цифр 10. Каждое число в этом N-пространственном векторе представляет собой вероятность конкретного класса. Например, если результирующий вектор для программы распознавания цифр это [0 0,1 0,1 0,75 0 0 0 0 0 0,05], значит существует 10% вероятность, что на изображении "1", 10% вероятность, что на изображение "2", 75% вероятность — "3", и 5% вероятность — "9".
Способ, с помощью которого работает полносвязный слой — это обращение к выходу предыдущего слоя (который, должен выводить высокоуровневые карты свойств) и определение свойств, которые больше коррелируют с определенным классом. Например, если программа предсказывает, что на каком-то изображении собака, у карт свойств, которые отражают высокоуровневые характеристики, такие как 4 лапы, должны быть высокие значения. Точно так же, если программа распознаёт, что на изображении птица — у неё будут высокие значения в картах свойств, представленных высокоуровневыми характеристиками вроде крыльев или клюва.
Обучение
Наиболее простым и популярным способом обучения является метод обучения с учителем (на маркированных данных) — метод обратного распространения ошибки и его модификации. До момента построения СНС, веса или значения фильтров случайны. Фильтры нижних слоёв не умеют искать границы и кривые, а фильтры верхних слоёв не умеют искать лапы и клювы. Как в аналогии с мозгом, кода ребенок рождается, он не может распознать кошку, собаку или птицу, ребенок становится старше и взрослые показывают ему разные картинки и изображения и присваивают им соответствующие ярлыки. Та же идея с обучением на картинках с присвоенными ярлыками является основой процесса обучения нейронной сети. Т.е. в нашем простейшем примере, набором для обучения может быть набор картинок в котором тысячи изображений собак, кошек и птиц. И у каждого изображения есть ярлык с названием животного.
Метод обратного распространения ошибки можно разделить на 4 отдельных блока: прямое распространение, функцию потери, обратное распространение и обновление веса. Во время прямого распространения, берётся тренировочное изображение — в нашем примере, это матрица 32х32х3 — и пропускается через всю сеть. В первом обучающем примере, так как все веса или значения фильтра были инициализированы случайным образом, выходным значением будет что-то вроде [.1 .1 .1 .1 .1 .1 .1 .1 .1 .1], то есть такое значение, которое не даст предпочтения какому-то определённому числу. Сеть с такими весами не может найти свойства базового уровня и не может обоснованно определить класс изображения. Это ведёт к функции потери. Но т.к. это процесс обучения, то используются обучающие данные. У таких данных есть и изображение, и ярлык. Допустим, первое обучающее изображение — это цифра 3. Ярлыком изображения будет [0 0 0 1 0 0 0 0 0 0]. Функция потери часто выражается СКО (среднеквадратической ошибкой), это 1/2 умножить на (реальность — предсказание) в квадрате.
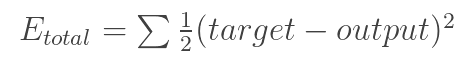
Потеря для первых двух обучающих изображений будет очень высокой. Необходимо добиться того, чтобы спрогнозированный ярлык (вывод свёрточного слоя) был таким же, как ярлык обучающего изображения (это значит, что сеть сделала верное предположение). Чтобы такого добиться, нужно свести к минимуму количество потерь. Нужно выяснить, какие входы (веса, в нашем случае) самым непосредственным образом способствовали потерям (или ошибкам) сети.
Один из способов визуализировать идею минимизации потери — это трёхмерный график, где веса нейронной сети (очевидно их больше, чем 2, но тут пример упрощен) это независимые переменные, а зависимая переменная — это потеря. Задача минимизации потерь — отрегулировать веса так, чтобы снизить потерю. Визуально нам нужно приблизиться к самой нижней точке чашеподобного объекта. Чтобы добиться этого, нужно найти производную потери (в рамках нарисованного графика — рассчитать угловой коэффициент в каждом направлении) с учётом весов).
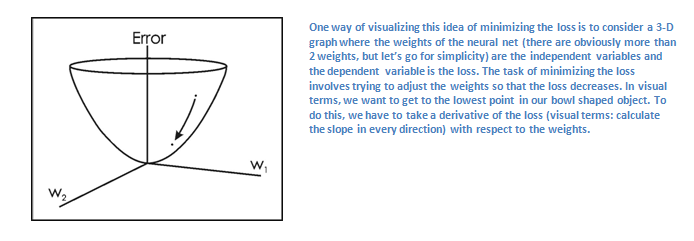
Это математический эквивалент dL/dW, где L —, это значение потери, W — веса определенного слоя. Теперь нужно выполнить обратное распространение через сеть, которое определяет, какие веса оказали большее влияние на потери, и найти способы, как их настроить, чтобы уменьшить потери. После вычисления производной, надо обновить веса так, чтобы они менялись в направлении градиента.
Скорость обучения — это параметр, который выбирается разработчиком. Высокая скорость обучения означает, что в обновлениях веса делались более крупные шаги, поэтому образцу может потребоваться меньше времени, чтобы набрать оптимальный набор весов. Но слишком высокая скорость обучения может привести к очень крупным и недостаточно точным скачкам, которые помешают достижению оптимальных показателей.
Процесс прямого распространения, функцию потери, обратное распространение и обновление весов, обычно называют одним периодом дискретизации (или epoch — эпохой). Программа будет повторять этот процесс фиксированное количество раз для каждого тренировочного изображения. После того, как обновление параметров завершится на последнем тренировочном образце, сеть в теории должна быть достаточно хорошо обучена и веса слоёв настроены правильно.
Тестирование
Чтобы проверить, работает ли СНС, берется другой набор изображений и ярлыков и пропускается через сеть, результат вывода сети сравнивается с правильными данными.