The goal of this report is to show how the asymetric encryption has been implemented into RSAp.

User interface

This mobile app is divided into multiple activities

Main page

On this first page, the user can generate a new public/private key pair with the length he wants (generate a 4096 bits length key pair may be quite time consuming). The private key is directly saved into the app storage and the public one is saved into the download directory of the phone

Encrypt a message

From the main menu, the user can go to this activity to encrypt a text file or a text input with a public key he received. This will generate a text file with the crypted message. This file will be save into the download directory

Sign a message

With this activity, the user can sign a text file or a text input with a public key. This will generate a signature file saved into the download directory of the phone

Check the signature of a message

With this activity, the user can check the integrity of a message.

The magic behind

Now I introduce you how to use this app, I can now show you the magic behind the asymetric encryption

RSA - Key generation

The RSA (Rivest–Shamir–Adleman) uses a pair of 2 separates keys :

• The private key is keep by the person Bob who generated the pair
• The public key is gave to the people who want to communicate with him Alice

To get those two keys, this algorithm is used :

1. Choose 2 distinct prime number p and q
2. Compute n = pq
3. Compute φ(n) = (p - 1)(q - 1)
4. Choose 1 random integer e which verify 1 < e < φ(n)
5. Compute d ≡ e^-1 (mod φ(n))

The couple (e,n) is the public key and (d,n) is the private key

Encrypt	Decrypt
M ≡ m^e (mod n)	m ≡ M^d (mod n)

with:

• M: The encrypted message
• m: The plain text message

RSA - Limits

The algorithm is widely uses on the computer world nowadays but may be quite expensive in terms of key computation especially for large keys (4096 bits) on mobile devices. Large keys take also more space on the internal storage.

The solution : ECC algorithm

The ECC (Elliptic Curve Cryptography) algorithm is used for website certificates signing but also as the key stone for the Bitcoin. In fact, this cryptosystem is more efficient in terms of computation use and reach the same level of security of RSA but with a shorter key length as in the chart bellow.

ECC	RSA
163	1024
233	2048
283	3072
409	7680
571	15360

This made the cryptosystem well fitted for the mobile devices and websites by being more efficiant and allowing shorter key with the same level of security.

ECC - How it works ?

ECC uses a mathematical object called elliptic curve

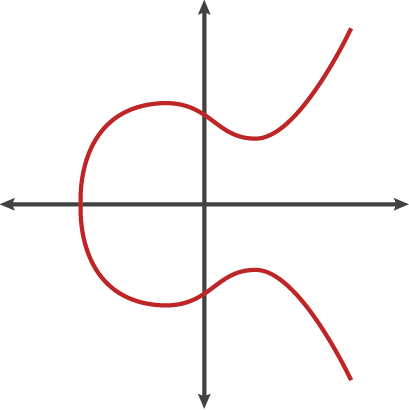Example of elliptic curve

As RSA, ECC is based on a trapdoor function. In other, it is easy to get B from A, but much harder to get A from B.

When we choose a point A on the curve add multiply d (by doting), we get another point on the same curve.

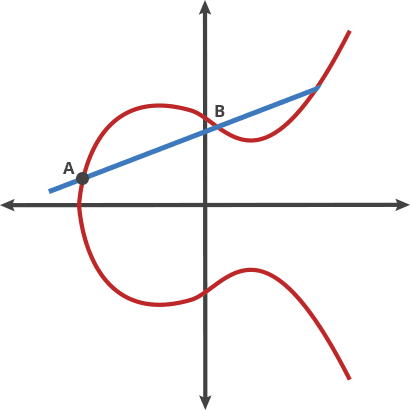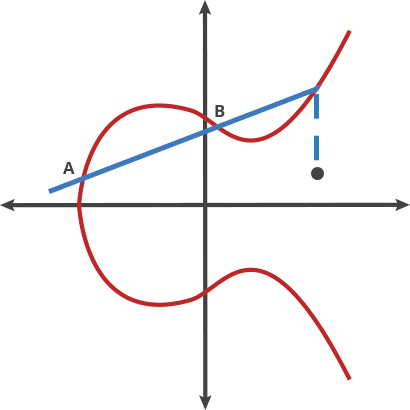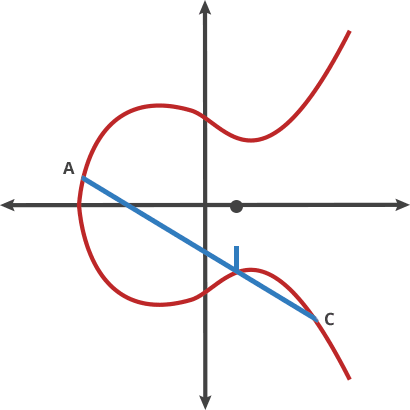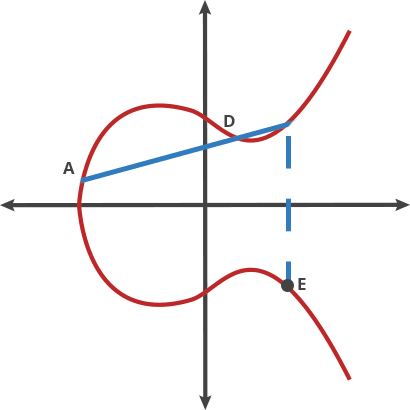Example of point dotting

A dot A = 2A = B
A dot B = 3A = C
A dot C = 4A = D ...

By getting D (public key) it's very hard to find the number 4 (private key). This computation is called discrete logarithm problem.
Despite almost three decades of research, mathematicians still haven't found an algorithm to solve this problem that improves upon the naive approach.

ECC - Key generation

With this object, we can generate the key pair :

1. EC function : y^2 = x^3 + ax + b
2. Choose a and b
3. Pick a point called generator on the curve : (Gx,Gy)
4. Pick a random generated prime number p
5. Pick a random generated integer n
6. Pick a random generated integer d which verify d < n
7. Compute Q = dG

Q is the public key and d is the private key

For example, the bitcoin uses these parameters :

• a = 0
• b = 8
• Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
• Gy = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
• p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
• n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
• d = 0x51897b64e85c3f714bba707e867914295a1377a7463a9dae8ea6a8b914246319

ECC - Limits

Even if ECC may be better than RSA, the choice of the parameters for the key generation may have a consequences on the strength of the keys. If d is too low, it may be easy to guess it by brut force.