Materi 9 : Eksplorasi Regresi - ThesionMS/Exploratory-Data-Analysis GitHub Wiki
Materi Pembelajaran: Pengantar Regresi
1.1 Pengantar Regresi
1.1.1 Definisi Regresi dalam Analisis Statistik
Regresi adalah suatu metode statistik yang digunakan untuk menemukan dan memodelkan hubungan antara satu atau lebih variabel independen (X) dengan variabel dependen (Y). Tujuan utama regresi adalah untuk membuat model matematis yang dapat digunakan untuk memprediksi atau menjelaskan nilai variabel dependen berdasarkan nilai variabel independen.
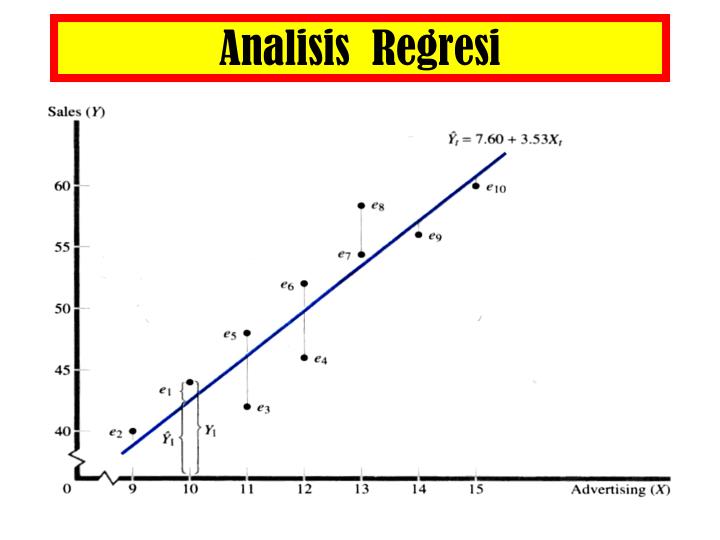
1.1.2 Tujuan Regresi dalam Analisis Statistik
Tujuan regresi dapat dibagi menjadi dua kategori utama:
- Prediksi: Memprediksi nilai variabel dependen (Y) berdasarkan nilai variabel independen (X).
- Eksplanasi: Menjelaskan hubungan sebab-akibat antara variabel dependen dan independen.
1.1.3 Perbedaan antara Variabel Independen dan Dependen
- Variabel Independen (X): Variabel yang dianggap sebagai penyebab atau variabel yang mempengaruhi variabel lain.
- Variabel Dependen (Y): Variabel yang dipengaruhi atau yang nilainya ingin diprediksi atau dijelaskan oleh variabel independen.
1.1.4 Contoh Sederhana
Misalnya, jika kita ingin memprediksi hasil ujian (Y) berdasarkan jumlah jam belajar (X), maka:
- Variabel Independen (X): Jumlah jam belajar.
- Variabel Dependen (Y): Hasil ujian.
II. Garis Regresi pada Model Regresi
2.1 Konsep Garis Regresi
Definisi Garis Regresi: Garis regresi adalah representasi visual dari model regresi linier yang menunjukkan hubungan antara variabel independen (X) dan variabel dependen (Y). Garis ini mencoba memodelkan pola hubungan linier di antara data.
Konsep Dasar:
- Garis regresi dihasilkan oleh persamaan matematis yang mencocokkan pola hubungan antara X dan Y.
- Tujuan garis regresi adalah memberikan estimasi yang paling baik tentang nilai Y berdasarkan nilai X.
Fungsi Matematis Garis Regresi: [ Y = mx + b ]
- ( Y ) adalah variabel dependen.
- ( X ) adalah variabel independen.
- ( m ) adalah koefisien kemiringan (slope).
- ( b ) adalah intercept.
Visualisasi Grafis:
- Scatter plot digunakan untuk mengilustrasikan distribusi data.
- Garis regresi ditambahkan ke plot untuk menunjukkan tren keseluruhan data.
import matplotlib.pyplot as plt
import numpy as np
# Contoh data
X = np.array([1, 2, 3, 4, 5,6,7,8,9,10])
Y = np.array([10,8,6,4,2,6,5,4,8,2])
# Plot scatter plot
plt.scatter(X, Y, label='Data Points')
# Menerapkan garis regresi
m, b = np.polyfit(X, Y, 1)
plt.plot(X, m*X + b, color='red', label='Regression Line')
# Menambahkan label dan legenda
plt.xlabel('Variabel Independen (X)')
plt.ylabel('Variabel Dependen (Y)')
plt.legend()
# Menampilkan plot
plt.show()
2.2 Menerapkan Garis Regresi
Langkah-langkah praktis untuk menerapkan garis regresi pada model regresi.
Visualisasi Data dengan Scatter Plot:
- Scatter plot memberikan gambaran visual hubungan antara variabel X dan Y.
- Poin-poin diplot sesuai dengan pasangan nilai X dan Y dari data.
# Contoh data
X = np.array([1, 2, 3, 4, 5,6,7,8,9,10])
Y = np.array([10,8,6,4,2,6,5,4,8,2])
# Plot scatter plot
plt.scatter(X, Y, label='Data Points')
plt.xlabel('Variabel Independen (X)')
plt.ylabel('Variabel Dependen (Y)')
plt.legend()
plt.show()
Perhitungan Koefisien Kemiringan dan Intercept:
- Menggunakan metode kuadrat terkecil (Least Squares Method).
- Koefisien kemiringan (( m )) dan intercept (( b )) dihitung untuk meminimalkan jumlah kuadrat selisih antara nilai prediksi dan nilai sebenarnya.
# Menghitung koefisien kemiringan dan intercept
m, b = np.polyfit(X, Y, 1)
print(f'Koefisien Kemiringan (m): {m}')
print(f'Intercept (b): {b}')
Plotting Garis Regresi pada Scatter Plot:
- Setelah mendapatkan ( m ) dan ( b ), garis regresi ditambahkan ke scatter plot.
- Garis ini mencerminkan model prediksi berdasarkan hubungan linier yang diidentifikasi.
# Plot scatter plot dan garis regresi
plt.scatter(X, Y, label='Data Points')
plt.plot(X, m*X + b, color='red', label='Regression Line')
plt.xlabel('Variabel Independen (X)')
plt.ylabel('Variabel Dependen (Y)')
plt.legend()
plt.show()
Evaluasi Model dengan Mean Squared Error (MSE):
- Mengukur seberapa baik garis regresi memodelkan data.
- MSE menghitung rata-rata kuadrat selisih antara nilai prediksi dan nilai sebenarnya.
- Semakin rendah MSE, semakin baik model regresi memfitting data.
from sklearn.metrics import mean_squared_error
# Menghitung prediksi menggunakan model regresi
Y_pred = m*X + b
# Menghitung MSE
mse = mean_squared_error(Y, Y_pred)
print(f'Mean Squared Error (MSE): {mse}')
III. Eksplorasi Regresi Linier
3.1 Pendekatan Grafis
Pendekatan grafis merupakan langkah awal dalam eksplorasi regresi linier untuk memahami hubungan antara variabel independen dan dependen. Scatter plot menjadi alat visual utama dalam evaluasi hubungan linier.
Menggunakan Scatter Plot:
- Scatter plot memperlihatkan sebaran titik data pada grafik, dengan sumbu X dan Y mewakili variabel independen dan dependen.
- Pemeriksaan pola sebaran titik dapat memberikan indikasi apakah hubungan antara variabel bersifat linier.
Contoh Penerapan:
import matplotlib.pyplot as plt
import seaborn as sns
# Contoh data
X = [1, 2, 3, 4, 5]
Y = [2, 4, 5, 4, 5]
# Membuat scatter plot
plt.scatter(X, Y)
plt.title("Scatter Plot Variabel X dan Y")
plt.xlabel("Variabel X")
plt.ylabel("Variabel Y")
plt.show()
3.2 Uji Asumsi
Sebelum menerapkan model regresi linier, penting untuk menguji asumsi dasar. Salah satu uji yang umum digunakan adalah uji normalitas untuk memeriksa apakah distribusi data terdistribusi normal.
Menggunakan Uji Normalitas:
- Uji seperti uji Kolmogorov-Smirnov atau uji Shapiro-Wilk dapat digunakan untuk menguji normalitas data.
- Hipotesis nol dari uji normalitas adalah data terdistribusi normal.
Contoh Penerapan:
import numpy as np
from scipy import stats
# Membuat sampel data
data = np.random.normal(loc=0, scale=1, size=100)
# Melakukan uji Shapiro-Wilk
shapiro_test = stats.shapiro(data)
# Menampilkan statistik uji dan nilai p
print(f"Statistik Uji Shapiro-Wilk: {shapiro_test[0]}, p-value: {shapiro_test[1]}")
# Interpretasi hasil
if shapiro_test[1] > 0.05:
print("Hipotesis nol bahwa data terdistribusi normal tidak dapat ditolak.")
else:
print("Hipotesis nol bahwa data terdistribusi normal ditolak.")
Normalitas Residu
Residu dari model regresi harus terdistribusi normal. Ini penting karena banyak uji statistik yang digunakan dalam inferensi statistik mengasumsikan normalitas. Untuk menguji normalitas residu, kita bisa menggunakan uji Shapiro-Wilk atau uji Kolmogorov-Smirnov.
Contoh kode untuk uji Shapiro-Wilk:
import numpy as np
import statsmodels.api as sm
from scipy import stats
# Misalkan kita memiliki model regresi
# X adalah matriks fitur, y adalah vektor target
X = np.random.rand(100, 2)
y = X @ np.array([1.5, -3.2]) + np.random.randn(100)
# Menambahkan konstanta ke X untuk intercept
X = sm.add_constant(X)
# Membuat model regresi linier dan melakukan fitting
model = sm.OLS(y, X).fit()
# Mendapatkan residu dari model
residu = model.resid
# Melakukan uji Shapiro-Wilk
shapiro_test = stats.shapiro(residu)
print(f"Shapiro-Wilk test statistic: {shapiro_test}, p-value: {shapiro_test}")
Homoskedastisitas
Variabilitas (varians) dari residu seharusnya konsisten untuk semua tingkat nilai prediktor. Homoskedastisitas dapat diuji dengan uji Breusch-Pagan atau uji White.
Contoh kode untuk uji Breusch-Pagan:
from statsmodels.stats.diagnostic import het_breuschpagan
# Melakukan uji Breusch-Pagan
bp_test = het_breuschpagan(residu, model.model.exog)
labels = ['Lagrange multiplier statistic', 'p-value', 'f-value', 'f p-value']
# Menampilkan hasil uji Breusch-Pagan
print("Hasil Uji Breusch-Pagan:")
print(dict(zip(labels, bp_test)))
# Menentukan tingkat signifikansi
alpha = 0.05
# Menentukan keputusan berdasarkan p-value
p_value = bp_test[1]
# Menampilkan kesimpulan
if p_value < alpha:
print(f"\nKesimpulan: Tolak hipotesis nol. Terdapat bukti cukup untuk heteroskedastisitas.")
else:
print(f"\nKesimpulan: Terima hipotesis nol. Tidak terdapat bukti cukup untuk heteroskedastisitas.")
Linearitas Hubungan
Asumsi linearitas menyatakan bahwa hubungan antara variabel independen (prediktor) dan variabel dependen (respon) harus linier. Ini berarti bahwa perubahan pada variabel independen diharapkan menghasilkan perubahan proporsional pada variabel dependen. Untuk memeriksa asumsi ini, kita dapat menggunakan plot residu terhadap nilai-nilai prediksi atau nilai-nilai variabel independen. Jika plot menunjukkan pola yang sistematis (misalnya, bentuk kurva atau pola tertentu), ini mungkin menunjukkan bahwa hubungan tersebut tidak linier.
Contoh kode untuk memeriksa linearitas dengan plot residu:
import matplotlib.pyplot as plt
import statsmodels.api as sm
# Misalkan kita memiliki model regresi yang sudah di-fit
# model adalah objek hasil fitting dari statsmodels
# Mendapatkan nilai prediksi
fitted_values = model.fittedvalues
# Plot residu terhadap nilai prediksi
plt.scatter(fitted_values, residu)
plt.xlabel('Fitted Values')
plt.ylabel('Residu')
plt.title('Residu vs. Fitted Plot')
plt.axhline(0, color='red', linestyle='--')
plt.show()
Tidak Ada Multikolinearitas
Multikolinearitas adalah kondisi di mana dua atau lebih variabel independen dalam model regresi memiliki korelasi yang tinggi satu sama lain. Hal ini dapat menyebabkan masalah dalam estimasi koefisien regresi karena variabel-variabel tersebut tidak memberikan informasi yang independen. Dengan kata lain, variabel-variabel tersebut mungkin mengandung informasi yang sama atau serupa, sehingga sulit untuk menentukan kontribusi masing-masing variabel terhadap variabel dependen.
Multikolinearitas dapat menyebabkan beberapa masalah, seperti:
- Koefisien regresi menjadi tidak stabil, di mana perubahan kecil pada data dapat menyebabkan perubahan besar pada koefisien.
- Standar error dari koefisien menjadi besar, yang mengurangi keandalan uji statistik.
- Sulitnya interpretasi model karena tidak jelasnya pengaruh individu dari masing-masing variabel independen.
Untuk mendeteksi multikolinearitas, kita dapat menggunakan beberapa metode, salah satunya adalah dengan menghitung Variance Inflation Factor (VIF). VIF mengukur seberapa banyak varians dari koefisien regresi yang meningkat karena adanya korelasi antar variabel independen. Sebagai aturan umum, nilai VIF yang lebih besar dari 10 menunjukkan adanya multikolinearitas yang kuat.
Contoh kode untuk menghitung VIF menggunakan Python:
import pandas as pd
import numpy as np
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant
# Membuat DataFrame
X = np.random.rand(100, 2)
y = X @ np.array([1.5, -3.2]) + np.random.randn(100)
df = pd.DataFrame(data=np.column_stack((X, y)), columns=['Feature1', 'Feature2', 'Target'])
# Menambahkan konstanta untuk intercept
X = add_constant(X)
# Mengubah X menjadi DataFrame
X_df = pd.DataFrame(X, columns=['const', 'Feature1', 'Feature2'])
# Menghitung VIF untuk setiap variabel independen
vif_data = pd.DataFrame()
vif_data["feature"] = X_df.columns
vif_data["VIF"] = [variance_inflation_factor(X_df.values, i) for i in range(X_df.shape[1])]
print(vif_data)
IV. Eksplorasi Regresi Non-Linier
Regresi non-linier adalah pendekatan analisis regresi di mana data diikuti oleh model yang kemudian direpresentasikan sebagai fungsi matematika. Berbeda dengan regresi linier yang menghubungkan dua variabel (X dan Y) dengan fungsi garis lurus, regresi non-linier menggunakan fungsi yang lebih kompleks untuk menghasilkan kurva yang sesuai dengan data.
4.1 Pendekatan Fungsional
Dalam pendekatan fungsional, kita harus memilih bentuk fungsional yang paling sesuai dengan pola data yang kita miliki. Beberapa contoh fungsi non-linier yang umum digunakan adalah:
- Fungsi kuadratik: ( y = ax^2 + bx + c )
- Fungsi eksponensial: ( y = ae^{bx} )
- Fungsi logaritmik: ( y = a + b\log(x) )
- Fungsi kekuatan: ( y = ax^b )
Pemilihan bentuk fungsional yang tepat sangat penting karena akan mempengaruhi kemampuan model untuk menangkap hubungan antara variabel independen dan dependen.
4.2 Penyesuaian Model
Setelah memilih fungsi yang sesuai, kita perlu mengimplementasikan model regresi non-linier. Ini melibatkan penyesuaian parameter model untuk meminimalkan kesalahan antara nilai yang diprediksi oleh model dan nilai yang sebenarnya dari data. Kita dapat menggunakan berbagai metode optimasi untuk menemukan parameter yang optimal.
4.3 Evaluasi Model
Evaluasi model regresi non-linier melibatkan penggunaan metrik untuk menilai seberapa baik model memprediksi data. R-squared yang disesuaikan adalah salah satu metrik yang sering digunakan, yang mengukur proporsi varians dalam variabel dependen yang dapat dijelaskan oleh model, dengan mempertimbangkan jumlah variabel independen dalam model.
Contoh Kode Regresi Non-Linier dengan Python
Berikut adalah contoh kode untuk mengimplementasikan dan mengevaluasi model regresi non-linier menggunakan Python dengan library scikit-learn:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# Contoh data.
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
y = np.array([2, 3.5, 5, 6.5, 8, 10.5, 13, 15.5, 18, 20.5])
# Mendefinisikan fungsi model, misalnya fungsi kuadratik.
def model_func(x, a, b, c):
return a * x**2 + b * x + c
# Melakukan curve fitting.
params, covariance = curve_fit(model_func, x, y)
# Mendapatkan parameter a, b, dan c dari fitting.
a, b, c = params
# Membuat data prediksi dari model.
x_pred = np.linspace(0, 11, 100) # Data x untuk prediksi
y_pred = model_func(x_pred, a, b, c)
# Visualisasi data asli dan model yang di-fit.
plt.scatter(x, y, label='Data Asli')
plt.plot(x_pred, y_pred, color='red', label='Model yang Di-fit')
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Regresi Non-Linier Menggunakan Fungsi Kuadratik')
plt.show()
# Menampilkan parameter model.
print(f"Parameter model: a = {a}, b = {b}, c = {c}")