Materi 2 ‐ Statistika Deskriptif dalam Analisis Eksplorasi Data - ThesionMS/Exploratory-Data-Analysis GitHub Wiki

Pendahuluan

Statistika deskriptif adalah cabang statistika yang berkaitan dengan pengumpulan, penyajian, dan interpretasi data. Ini merupakan langkah pertama dalam analisis data yang bertujuan untuk memahami karakteristik dasar dari suatu kumpulan data. Dalam modul ini, kita akan membahas pentingnya statistika deskriptif, dasar-dasar pemusatan data, metode pemusatan data, dan konsep-konsep penting seperti kurtosis dan skewness.

1. Pentingnya Statistika Deskriptif dalam Analisis Eksplorasi Data

Esensi Statistika Deskriptif

Sebagaimana yang dikutip dari buku "Hands-On Exploratory Data Analysis with Python" oleh Suresh Kumar Mukhiya dan Usman Ahmed, "Descriptive statistics, assist in describing and comprehending datasets by providing a short summary pertaining to the dataset provided". Esensi statistika deskriptif dalam analisis eksplorasi data adalah memberikan pemahaman singkat tentang karakteristik dasar dari suatu kumpulan data. Ini merupakan langkah pertama yang penting dalam proses analisis data dan memiliki beberapa tujuan utama:

1. Ringkasan Data: Statistika deskriptif membantu dalam merangkum data dengan metode yang sederhana dan informatif. Dengan menghasilkan statistik seperti rata-rata, median, modus, varians, standar deviasi, kuartil, skewness, dan kurtosis, kita dapat memberikan gambaran yang lebih jelas tentang distribusi dan properti data.

2. Identifikasi Pola: Statistika deskriptif membantu mengidentifikasi pola dalam data. Ini memungkinkan kita untuk melihat apakah ada tren atau pola tersembunyi, apakah data tersebut condong ke satu sisi, dan apakah ada outlier (data yang ekstrem).

3. Data Preprocessing: Sebelum melangkah ke analisis yang lebih mendalam, statistika deskriptif dapat digunakan untuk mengidentifikasi dan mengatasi masalah dalam data seperti missing values atau data yang tidak valid.

4. Komunikasi Data: Statistika deskriptif memberikan alat untuk berkomunikasi dengan orang lain tentang data. Dengan memberikan ringkasan statistik, kita dapat menjelaskan karakteristik data secara efektif kepada rekan kerja, pemangku kepentingan, atau pemilik proyek.

5. Pengambilan Keputusan Awal: Hasil statistika deskriptif dapat digunakan untuk mengambil keputusan awal. Misalnya, jika rata-rata suatu parameter di bawah batas tertentu, ini dapat menjadi sinyal bahwa tindakan perbaikan diperlukan.

6. Penyelidikan Lanjutan: Statistika deskriptif sering digunakan sebagai dasar untuk analisis lebih lanjut. Data yang telah diringkas dengan baik melalui statistika deskriptif dapat digunakan dalam berbagai teknik analisis statistik seperti regresi, pengujian hipotesis, dan analisis multivariat.

EDA adalah proses analisis data untuk merangkum karakteristik utama dan mengidentifikasi pola, tren, dan hubungan. Statistik deskriptif membantu kita mencapai tujuan ini dengan memberikan ringkasan singkat tentang data, termasuk ukuran pemusatan data (seperti mean, median, dan modus) dan ukuran keragaman (seperti deviasi standar dan rentang).

Dengan menggunakan statistik deskriptif, kita dapat memperoleh wawasan tentang distribusi, keragaman, dan karakteristik lain dari data kita. Informasi ini kemudian dapat digunakan untuk mengidentifikasi nilai-nilai yang berbeda dari kebanyakan, mendeteksi pola, dan membuat keputusan yang berdasar tentang cara lebih lanjut menganalisis data. Statistik deskriptif juga memberikan dasar bagi teknik statistik yang lebih canggih, seperti statistik inferensial, yang digunakan untuk membuat prediksi dan menyimpulkan tentang populasi yang lebih besar berdasarkan sampel data.

Implementasi dalam Python

import pandas as pd
data = pd.read_csv('data.csv')
summary = data.describe()
print(summary)

2. Dasar-dasar Pemusatan Data

Metode pemusatan data adalah teknik statistik yang digunakan untuk menemukan nilai pusat atau "lokasi tengah" dari suatu kumpulan data. Ini membantu kita dalam memahami distribusi data dan memberikan informasi tentang di mana sebagian besar data terkonsentrasi, dalam kata lain mengidentifikasi nilai yang mewakili sebagian besar data. Beberapa metode pemusatan data yang umum digunakan adalah rata-rata (mean), median, dan modus.

Implementasi dalam Python

import numpy as np
data = [12, 15, 18, 21, 24, 27, 30]
mean = np.mean(data)
median = np.median(data)
print("Rata-rata:", mean)
print("Median:", median)

3. Metode Pemusatan Data

3.1 Rata-rata, Median, dan Modus

1. Rata-Rata (Mean):

   • Rata-rata adalah nilai yang dihitung dengan menjumlahkan semua angka dalam data dan kemudian membaginya dengan jumlah total angka.
   • Rata-rata memberikan indikasi tentang nilai tengah secara aritmatika dari data.

   Contoh Interpretasi: Dalam studi kasus penghasilan bulanan karyawan di sebuah perusahaan, rata-rata penghasilan adalah $3.500. Ini berarti secara rata-rata, karyawan di perusahaan ini memiliki penghasilan sekitar $3.500 per bulan.

2. Median:

   • Median adalah nilai tengah dalam data ketika data diurutkan. Jika jumlah data ganjil, median adalah angka di tengah; jika jumlah data genap, median adalah rata-rata dari dua angka tengah.
   • Median digunakan ketika ada outlier atau data yang sangat terpengaruh oleh nilai ekstrem.

   Contoh Interpretasi: Dalam studi kasus distribusi umur siswa di sebuah sekolah, median usia adalah 15 tahun. Ini berarti setengah dari siswa berusia di bawah 15 tahun dan setengah lagi berusia di atas 15 tahun.

3. Modus:

   • Modus adalah nilai yang paling sering muncul dalam kumpulan data.
   • Modus digunakan ketika kita ingin mengetahui nilai yang paling umum atau dominan dalam data.

   Contoh Interpretasi: Dalam studi kasus frekuensi warna mobil di sebuah dealer, modusnya adalah "hitam". Ini berarti mobil berwarna hitam adalah yang paling banyak dijual di dealer tersebut.

Pemahaman tentang metode pemusatan data ini sangat penting dalam statistika deskriptif karena memberikan gambaran yang lebih baik tentang karakteristik data. Misalnya, jika kita hanya menggunakan rata-rata, kita mungkin akan terpengaruh oleh outlier yang ekstrem, sedangkan median dan modus dapat memberikan informasi yang lebih stabil tentang "nilai pusat" data.

Dalam studi kasus riil, pemusatan data dapat membantu pengambilan keputusan yang lebih baik. Misalnya, dalam analisis keuangan sebuah perusahaan, pemahaman tentang rata-rata pendapatan atau biaya dapat membantu manajemen merencanakan anggaran dan strategi bisnis. Dalam penelitian medis, median umur pasien dapat memberikan petunjuk tentang distribusi usia populasi yang mungkin memengaruhi diagnosis dan pengobatan. Oleh karena itu, metode pemusatan data merupakan alat penting dalam analisis eksplorasi data untuk mengambil wawasan yang berguna dari kumpulan data yang kompleks.

Implementasi dalam Python

data = [12, 15, 18, 21, 24, 27, 30, 30, 30]
mean = np.mean(data)
median = np.median(data)
mode = stats.mode(data)
print("Rata-rata:", mean)
print("Median:", median)
print("Modus:", mode.mode[0])

3.2 Range, Varians, dan Standar Deviasi

• Range adalah selisih antara nilai tertinggi (maksimum) dan nilai terendah (minimum) dalam kumpulan data.
• Range memberikan gambaran tentang sejauh mana data tersebar.

Contoh Interpretasi: Dalam studi kasus suhu harian di kota A, suhu tertinggi dalam sebulan adalah 35°C dan suhu terendahnya adalah 10°C. Jadi, range suhu bulanan adalah 35°C - 10°C = 25°C.

• Varians mengukur seberapa jauh setiap data dari rata-rata. Semakin besar varians, semakin tersebar data tersebut.
• Varians dihitung dengan mengambil rata-rata dari kuadrat selisih setiap data dengan rata-rata.

Contoh Interpretasi: Dalam studi kasus investasi, varians dari pengembalian saham tertentu adalah 0.04. Ini berarti pengembalian saham tersebut bervariasi sekitar 4% dari rata-rata pengembalian.

• Standar deviasi adalah akar kuadrat dari varians. Ini memberikan ukuran dispersi data yang lebih mudah dipahami dalam satuan yang sama dengan data.
• Standar deviasi yang lebih besar menunjukkan variabilitas yang lebih besar dalam data.

Contoh Interpretasi: Dalam studi kasus tingkat kepuasan pelanggan, standar deviasi dari skor kepuasan adalah 2.5. Ini mengindikasikan bahwa skor kepuasan pelanggan bervariasi sekitar 2.5 poin dari nilai rata-ratanya.

Implementasi dalam Python

data = [12, 15, 18, 21, 24, 27, 30]
range_val = np.ptp(data)
variance = np.var(data)
std_deviation = np.std(data)
print("Range:", range_val)
print("Varians:", variance)
print("Standar Deviasi:", std_deviation)

3.3 Kuartil

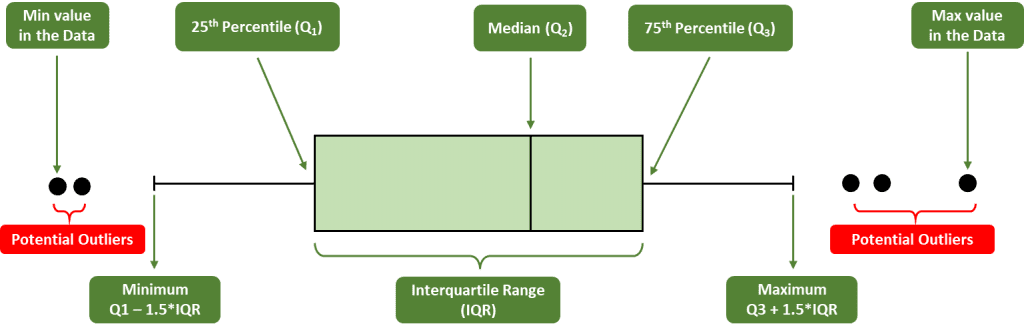
• Kuartil adalah nilai yang membagi data menjadi empat bagian sebanding, yang dikenal sebagai kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3).
• Kuartil pertama adalah median separuh data pertama, kuartil kedua adalah median seluruh data, dan kuartil ketiga adalah median separuh data kedua.

Contoh Interpretasi: Dalam studi kasus distribusi gaji karyawan di sebuah perusahaan, Q1 adalah $30.000, Q2 adalah $45.000, dan Q3 adalah $60.000. Ini berarti setengah karyawan memiliki gaji di bawah $45.000 dan setengah lainnya di atas $45.000.

Implementasi dalam Python

data = [12, 15, 18, 21, 24, 27, 30]
q1 = np.percentile(data, 25)
q2 = np.percentile(data, 50)
q3 = np.percentile(data, 75)
print("Kuartil Pertama (Q1):", q1)
print("Kuartil Kedua (Q2/Median):", q2)
print("Kuartil Ketiga (Q3):", q3)

4. Kurtosis dan Skewness

4.1 Kurtosis

• Kurtosis mengukur tajamnya atau kepipihan distribusi data. Nilai kurtosis yang tinggi menunjukkan distribusi data yang lebih tajam (leptokurtik), sementara nilai kurtosis yang rendah menunjukkan distribusi yang lebih datar (platykurtik).
• Kurtosis membantu kita memahami sejauh mana data memiliki ekor panjang atau distribusi yang "berbentuk".
• Dapat digolongkan menjadi tiga tipe: leptokurtik, mesokurtik, dan platykurtik.

Contoh Interpretasi: Dalam studi kasus hasil ujian siswa, kurtosis yang tinggi (+2.5) menunjukkan bahwa distribusi skor ujian memiliki puncak yang lebih tajam dan ekor yang lebih panjang, yang berarti ada konsentrasi yang tinggi pada skor tertentu.

4.2 Skewness

• Skewness mengukur asimetri distribusi data. Nilai skewness positif menunjukkan ekor panjang di sebelah kanan distribusi, sementara nilai skewness negatif menunjukkan ekor panjang di sebelah kiri distribusi.
• Skewness dapat membantu kita memahami sejauh mana distribusi data condong ke arah tertentu.

Contoh Interpretasi: Dalam studi kasus harga rumah di sebuah wilayah, skewness positif (+0.8) menunjukkan bahwa sebagian besar harga rumah berada di bawah harga rata-rata, sementara beberapa harga rumah sangat tinggi.

Implementasi dalam Python

from scipy.stats import kurtosis, skew
data = [12, 15, 18, 21, 24, 27, 30, 36, 42]
kurt = kurtosis(data)
skw = skew(data)
print("Kurtosis:", kurt)
print("Skewness:", skw)