Stanford Exercise 4 - SummerBigData/MattRepo GitHub Wiki

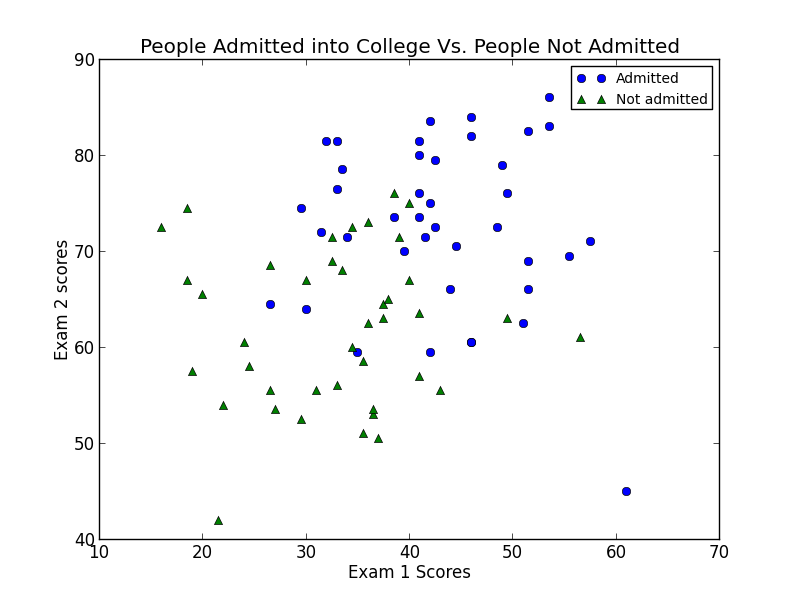
In this exercise we determined whether students were admitted into college or not based off of their exam 1 and 2 scores. We were give 2 sets of data. The first set consisted of 2 columns, the first one consisting of exam 1 scores and the second one consisting of exam 2 scores. The second set gave us an array of 1's and 0's, 1's indicating the student was admitted, 0's indicating they weren't. There was a total of 80 training examples. The plot below shows the scores of the students along with whether or not they were admitted. This was done by splitting the exam scores into two seperate arrays depending on if the student was admitted or not.

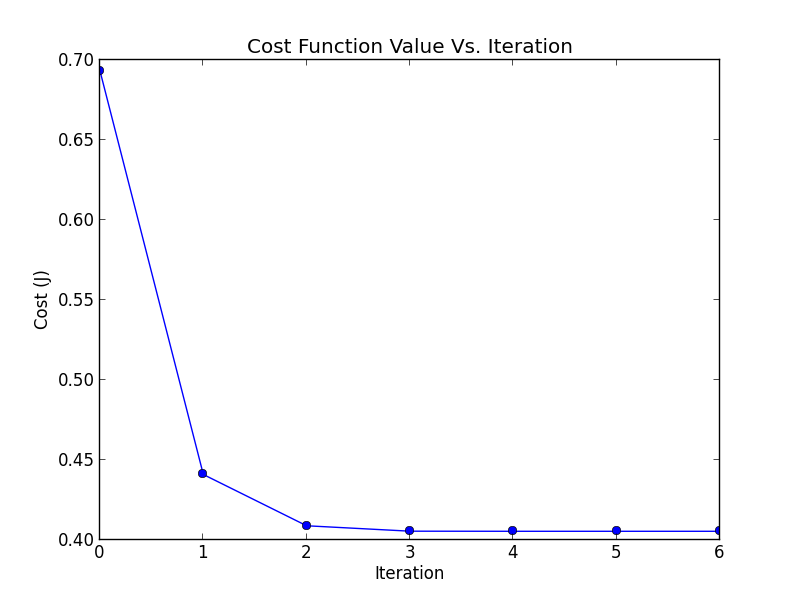
We used logistic regression to find the decision boundary line. We did this by using Newton's method to minimize our cost function and find our final theta values. In order to do this we had to use the gradient of the cost function and the Hessian to use Newton's method. Our hypothesis function this time was the sigmoid function. We were able to get Newton's method to converge after 7 iterations and our theta0, theta1, and theta2 values are -16.38, 0.148, and 0.159 respectively. The following plot shows the value of our cost function after each iteration until it converged.

The following plot shows the decision boundary that was calculated.

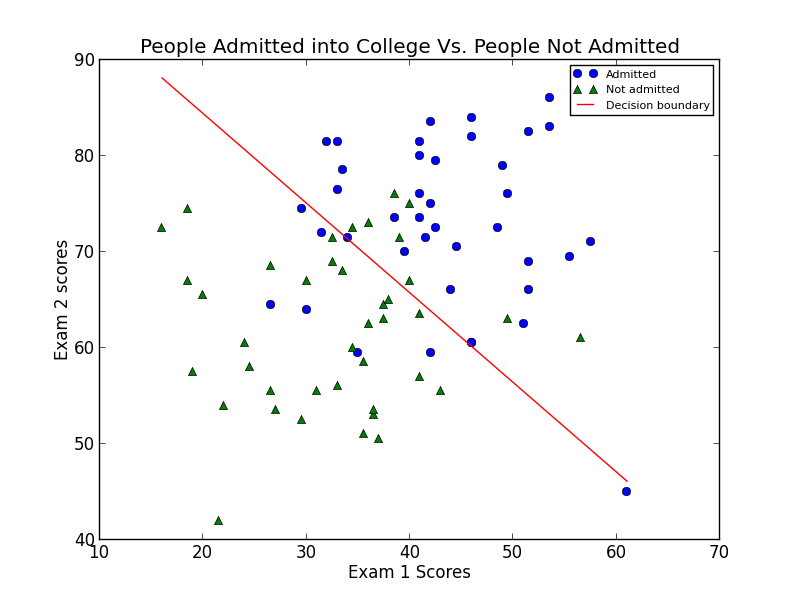
We found the probability that a student with a score of 20 on Exam 1 and a score of 80 on Exam 2 will not be admitted is 0.668, or 66.8%.