长期行情预测 - StupidCodeGenerator/StupidCodeGenerator.github.io GitHub Wiki

感觉走了很多弯路, 其实自己更在乎的不过就是在某一个时间点上盈利的期望值. 所以研究什么最高点最低点完全没蛋用.

所以现在统计的Y轴应该确定好了, 就是获利期望. 无论进行任何的统计, Y轴都可以确定好了就是 "某个时间点上, 未来N天获利的数学期望."

在只考虑理想情况的前提下, 可以认为未来的N天内, 虚拟的投资者在最高点出售股票. 我们假设卖出价格是O, 买入价格是I, 卖出价格的概率密度函数为P(O)

那么我们会的到当卖出价格为O的数学期望 E(O) = P(O) * (O-I)

对上式进行积分会的到在某一时间点的数学期望

有点混乱和模糊, 回头我仔细的整理一下, 但是大体上可以确定就是一定要将Y轴定义为获利期望, 否则就是浪费生命.

最后事实上是使用盈利的平均值来估计的期望值.

不过还有一个问题，就是N的取值范围。这个值我觉得可以被称为“交易周期“。可以给出一个价格范围内的最佳交易周期。也就是给定买入价格I，求N使O最大。

但是在对买入时机进行估计时，给定100天的这个范围有点太过草率，可以N从0到100给出一个最大的收益曲线

最后定的是0-200，计算量有点大，我的机器需要计算大概三个小时以上。我把计算结果按照N的值不同存成文件，然后依次保存到Github上。目前来说这个特征值还是比较稳定的。

现在已经计算到了160+的数据。如果用热图表示，X为N的值，Y为买入价格。但是matplotlib的imshow默认的x轴和y轴都是实际的像素值。所以自己只能够将目前已有的数据整合成一个二维数组，然后在单独计算出xy两个方向的比例并手动赋值。计算结果中的买入价格范围并不一致，需要看一下给出一个标准来。买入价格的“粒度”为0.5，所以结果的Y轴可以定为

{0,0.05,0.10,0.15,0.20,...2.95,3}

高于3的情况下数据密度比较低，所以可信度也比较低。如果在范围内出现了空值，就以0来填充。

http://blog.csdn.net/rumswell/article/details/9862089

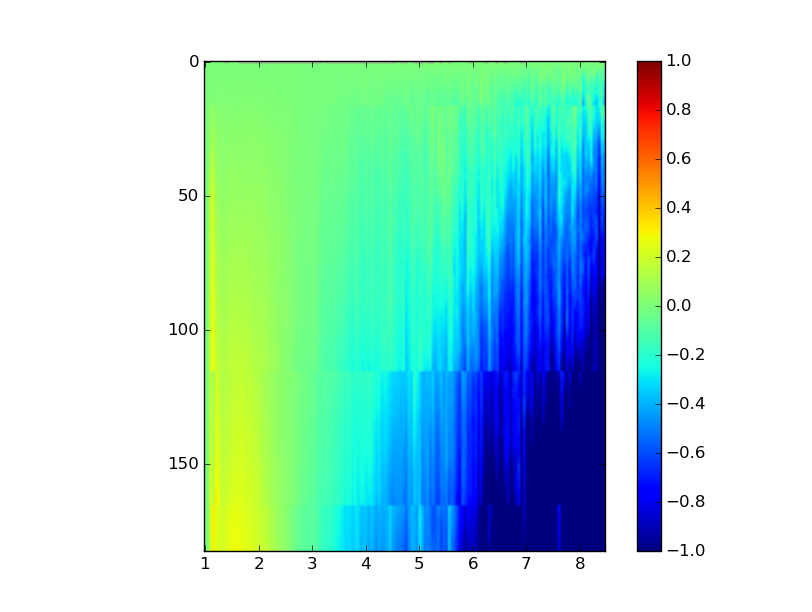
可以确定购买价格越低，盈利期望就越大。并且目前看来，买卖间隔越长，盈利期望越明显。所以说基本可以确定，股票投资应该谨慎选择入手价格并且尽可能的做长线，不要做短线。

##博客草稿

#股票的长期收益

我前面已经研究过，股票每一天的涨落基本上就是随机的。估计股票一天的涨落真的不那么容易，并且也有很大的风险。对于我这种初学者，对股票的长期收益分析才是比较简单也比较可靠的。我的思路就是既然股票的价格总体上服从对数正态分布，那么我们就能够使用当前的价格与最大概率的价格的比值，作为一个“相对价格”。

我们假设股票有一种相对价格回到1的趋势，因为这种价格有最大的出现概率。所以说我们可以统计一下在某相对价格买入，然后在N天以后卖出的期望收益。

根据从雅虎财经爬到的数据进行统计后，得到了这样的结果。

横坐标是买入时的相对价格，纵坐标是买入后的持有时间。持有时间以交易日计。持有时间我计算到了180+，已经能看到结论了，所以也没有必要继续往下算。从图上我们可以非常清楚的看到获利集中在长时间持有，并且在相对价格小于1时买入。

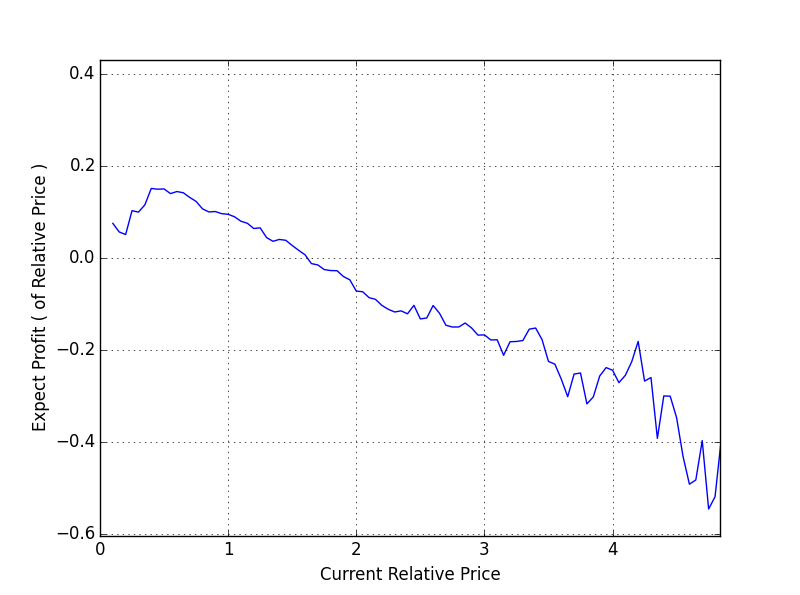
这张看的更清楚，这是持有100天的买入价格和获利期望的关系。

接下来的事情就比较简单了，我打算下一步就做。首先对能拿到的所有股票数据进行拟合，拟合结果越好证明这支股票越规律。然后选出那些非常规律并且相对价格小于1的股票，买入。什么时候涨了就买了就可以了。这种策略周期比较长，但是我认为风险很低。具体风险有多大，需要等我下一步研究。

#当前Fit函数的问题。

在计算估计值的过程中，发现拟合的结果实际上并不好。

所以可能改成这样好一些：统计某一个X值的邻域[x-n, x+n]，然后统计这个范围内的均值，画成曲线。然后求得最大值，和第二极大值。或者，干脆计算左侧和右侧的面积比。哦这个靠谱。