NMF (Non Negative Matrix Factorization) - SoojungHong/TextMining GitHub Wiki
Non Negative Matrix Factorization
Non-negative Matrix Factorization is a Linear-algeabreic model, that factors high-dimensional vectors into a low-dimensionality representation. Similar to Principal component analysis (PCA), NMF takes advantage of the fact that the vectors are non-negative. By factoring them into the lower-dimensional form, NMF forces the coefficients to also be non-negative.
Given the original matrix A, we can obtain two matrices W and H, such that A= WH. NMF has an inherent clustering property, such that W and H represent the following information about A:
A = W x H
A (Document-word matrix) — input that contains which words appear in which documents. W (Basis vectors) — the topics (clusters) discovered from the documents. H (Coefficient matrix) — the membership weights for the topics in each document.
We calculate W and H by optimizing over an objective function (like the EM algorithm), updating both W and H iteratively until convergence.
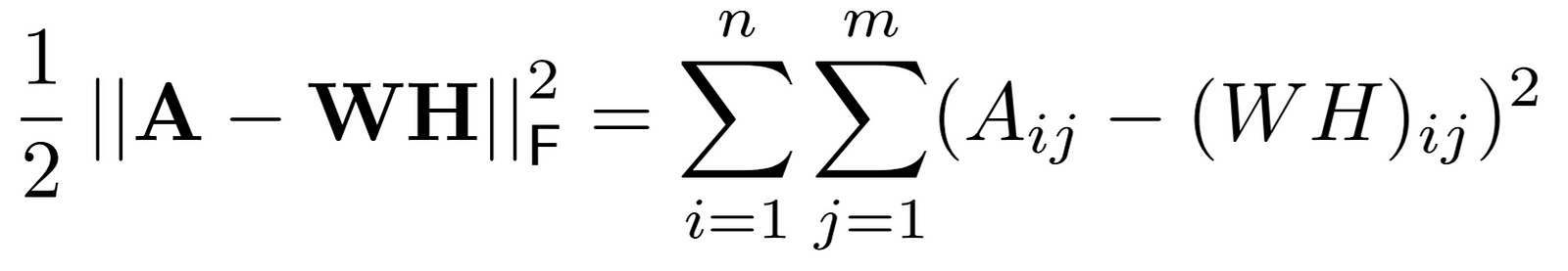
In this objective function, we measure the error of reconstruction between A and the product of it’s factors W and H, based on euclidean distance.
Using the objective function, the update rules for W and H can be derived, and we get:
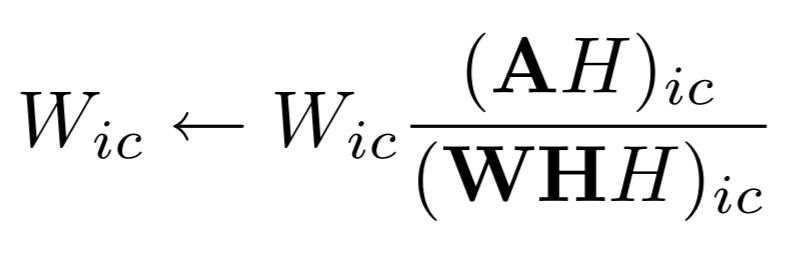
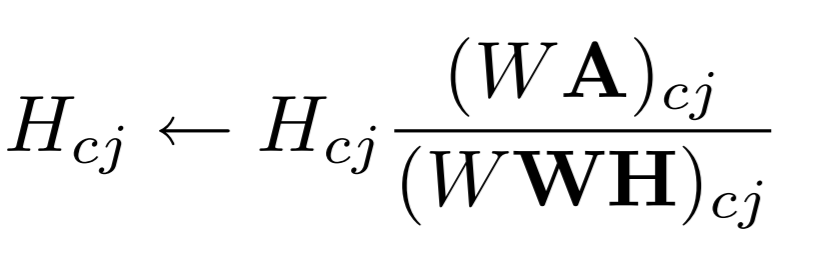
The updated values are calculated in parallel operations, and using the new W and H, we re-calculate the reconstruction error, repeating this process until convergence.