non normal distribution - SoojungHong/StatisticalMind GitHub Wiki
- Explain a probability distribution that is not normal and how to apply that?
First of all, what is normal distribution? A normal distribution, sometimes called the bell curve, is a distribution that occurs naturally in many situations. For example, the bell curve is seen in tests like the SAT and GRE. The bulk of students will score the average (C), while smaller numbers of students will score a B or D. An even smaller percentage of students score an F or an A. This creates a distribution that resembles a bell (hence the nickname). The bell curve is symmetrical. Half of the data will fall to the left of the mean; half will fall to the right.
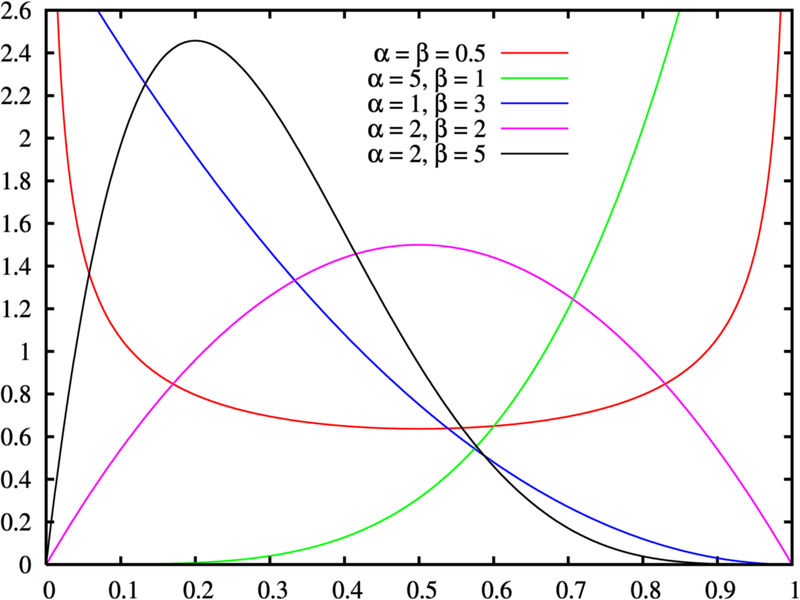
Following distributions are non normal distributions.
- Beta Distribution
- Exponential Distribution
- Gamma Distribution
- Inverse Gamma Distribution
- Log Normal Distribution
- Logistic Distribution
- Maxwell-Boltzmann Distribution
- Poisson Distribution
- Skewed Distribution
- Symmetric Distribution
- Uniform Distribution
- Unimodal Distribution
- Weibull Distribution
Reasons for the Non Normal Distribution
Many data sets naturally fit a non normal model. For example, the number of accidents tends to fit a Poisson distribution and lifetimes of products usually fit a Weibull distribution. However, there may be times when your data is supposed to fit a normal distribution, but doesn’t. If this is a case, it’s time to take a close look at your data.
- Outliers can cause your data the become skewed. The mean is especially sensitive to outliers. Try removing any extreme high or low values and testing your data again.
- Multiple distributions may be combined in your data, giving the appearance of a bimodal or multimodal distribution. For example, two sets of normally distributed test results are combined in the following image to give the appearance of bimodal data.
- Insufficient Data can cause a normal distribution to look completely scattered. For example, classroom test results are usually normally distributed. An extreme example: if you choose three random students and plot the results on a graph, you won’t get a normal distribution. You might get a uniform distribution (i.e. 62 62 63) or you might get a skewed distribution (80 92 99). If you are in doubt about whether you have a sufficient sample size, collect more data.
- Data may be inappropriately graphed. For example, if you were to graph people’s weights on a scale of 0 to 1000 lbs, you would have a skewed cluster to the left of the graph. Make sure you’re graphing your data on appropriately labeled axes.
Dealing with Non Normal Distributions
You have several options for handling your non normal data. Several tests, including the one sample Z test, T test and ANOVA assume normality. You may still be able to run these tests if your sample size is large enough (usually over 20 items). You can also choose to transform the data with a function, forcing it to fit a normal model. However, if you have a very small sample, a sample that is skewed or one that naturally fits another distribution type, you may want to run a non parametric test. A non parametric test is one that doesn’t assume the data fits a specific distribution type. Non parametric tests include the Wilcoxon signed rank test, the Mann-Whitney U Test and the Kruskal-Wallis test.
reference : http://www.statisticshowto.com/probability-and-statistics/non-normal-distributions/