How to deal with Non normal distribution - SoojungHong/StatisticalMind GitHub Wiki
Normally distributed data is needed to use a number of statistical tools, such as individuals control charts, Cp/Cpk analysis, t-tests and the analysis of variance (ANOVA).
Some people believe that all data collected and used for analysis must be distributed normally. But normal distribution does not happen as often as people think, and it is not a main objective. Normal distribution is a means to an end, not the end itself.
If a practitioner is not using such a specific tool, however, it is not important whether data is distributed normally. The distribution becomes an issue only when practitioners reach a point in a project where they want to use a statistical tool that requires normally distributed data and they do not have it.
Reason for non-normal distribution
When data is not normally distributed, the cause for non-normality should be determined and appropriate remedial actions should be taken. There are six reasons that are frequently to blame for non-normality.
Reason 1: Extreme Values
Too many extreme values in a data set will result in a skewed distribution. Normality of data can be achieved by cleaning the data. This involves determining measurement errors, data-entry errors and outliers, and removing them from the data for valid reasons.
It is important that outliers are identified as truly special causes before they are eliminated. Never forget: The nature of normally distributed data is that a small percentage of extreme values can be expected; not every outlier is caused by a special reason. Extreme values should only be explained and removed from the data if there are more of them than expected under normal conditions.
Reason 2: Overlap of Two or More Processes
Data may not be normally distributed because it actually comes from more than one process, operator or shift, or from a process that frequently shifts. If two or more data sets that would be normally distributed on their own are overlapped, data may look bimodal or multimodal – it will have two or more most-frequent values.
The remedial action for these situations is to determine which X’s cause bimodal or multimodal distribution and then stratify the data. The data should be checked again for normality and afterward the stratified processes can be worked with separately.
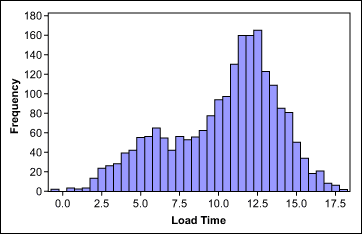
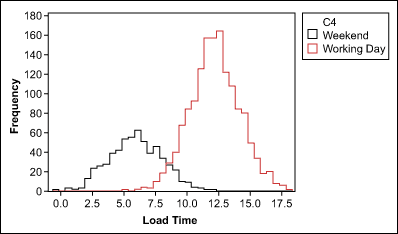
Reason 4: Sorted Data
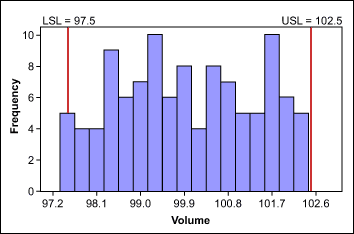
Collected data might not be normally distributed if it represents simply a subset of the total output a process produced. This can happen if data is collected and analyzed after sorting. The data in Figure 4 resulted from a process where the target was to produce bottles with a volume of 100 ml. The lower and upper specifications were 97.5 ml and 102.5 ml. Because all bottles outside of the specifications were already removed from the process, the data is not normally distributed – even if the original data would have been.
Reason 5: Values Close to Zero or a Natural Limit
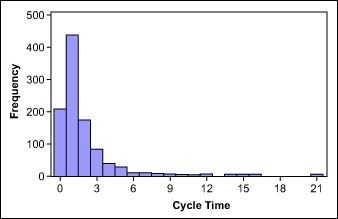
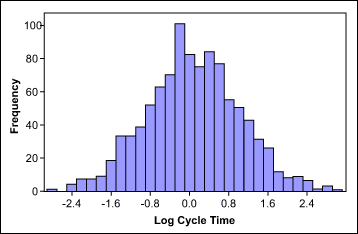
If a process has many values close to zero or a natural limit, the data distribution will skew to the right or left. In this case, a transformation, such as the Box-Cox power transformation, may help make data normal. In this method, all data is raised, or transformed, to a certain exponent, indicated by a Lambda value. When comparing transformed data, everything under comparison must be transformed in the same way.
Reason 6: Data Follows a Different Distribution
There are many data types that follow a non-normal distribution by nature. Examples include:
Weibull distribution, found with life data such as survival times of a product
Log-normal distribution, found with length data such as heights
Largest-extreme-value distribution, found with data such as the longest down-time each day
Exponential distribution, found with growth data such as bacterial growth
Poisson distribution, found with rare events such as number of accidents
Binomial distribution, found with “proportion” data such as percent defectives
No Normality Required
Comparison of Statistical Analysis Tools for Normally and Non-Normally Distributed Data
Tools for Normally Distributed data ++++ Equivalent Tools for Non-Normally Distributed Data +++ Distribution Required T-test (normal dist) Mann-Whitney test; Mood’s median test; Kruskal-Wallis test (non-normal dist) Any ANOVA (normal dist) Mood’s median test; Kruskal-Wallis test (non-normal dist) Any Paired t-test (normal dist) One-sample sign test (non-normal) Any
Some statistical tools do not require normally distributed data. To help practitioners understand when and how these tools can be used, the table below shows a comparison of tools that do not require normal distribution with their normal-distribution equivalents.
Reference :
https://www.isixsigma.com/tools-templates/normality/dealing-non-normal-data-strategies-and-tools/
http://www.statisticshowto.com/probability-and-statistics/non-normal-distributions/