Box Cox power transformation - SoojungHong/StatisticalMind GitHub Wiki
Making data normal using Box-Cox power transformation
Data transformation, and particularly the Box-Cox power transformation, is one of these remedial actions that may help to make data normal.
What are transformation?
Transforming data means performing the same mathematical operation on each piece of original data. Some transformation examples from daily life are currency exchange rates (e.g., U.S. dollar into Euros) and converting degree Celsius into degree Fahrenheit.
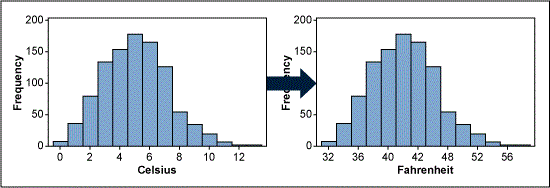
These two transformations are called linear transformations because the original data is simply multiplied or divided by a specific coefficient or a constant is subtracted or added. But these linear transformations do not change the shape of the data distribution and, therefore, do not help to make data look more normal.
Box-Cox transformation
Table 1: Common Box-Cox Transformations
l -- Y’
-2 -- Y^-2 = 1/Y^2
-1 -- Y^-1 = 1/Y^1
-0.5 -- Y^-0.5 = 1/(Sqrt(Y))
0 -- log(Y)
0.5 -- Y^0.5 = Sqrt(Y)
1 -- Y^1 = Y
2 -- Y^2
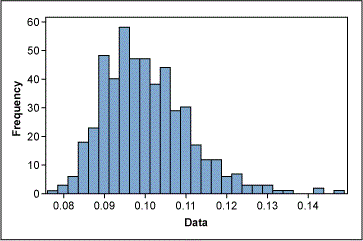
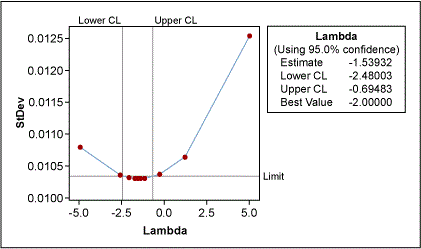
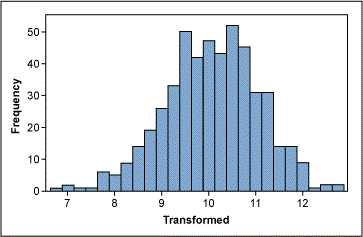
Figure 2 shows non-normally distributed cycle time data. Using the Box-Cox power transformation in a statistical analysis software program provides an output that indicates the best Lambda values
Does Box-Cox Power Transformation work?
The Box-Cox power transformation is not a guarantee for normality. This is because it actually does not really check for normality; the method checks for the smallest standard deviation. The assumption is that among all transformations with Lambda values between -5 and +5, transformed data has the highest likelihood – but not a guarantee – to be normally distributed when standard deviation is the smallest. Therefore, it is absolutely necessary to always check the transformed data for normality using a probability plot.
Additionally, the Box-Cox Power transformation only works if all the data is positive and greater than 0. This, however, can usually be achieved easily by adding a constant (c) to all data such that it all becomes positive before it is transformed. The transformation equation is then:
Y’ = (Y+C)^l
Python example
This example demonstrates the use of the Box-Cox transform through preprocessing.PowerTransformer to map data from various distributions to a normal distribution.
Box-Cox is useful as a transformation in modeling problems where homoscedasticity and normality are desired. Below are examples of Box-Cox applied to six different probability distributions: Lognormal, Chi-squared, Weibull, Gaussian, Uniform, and Bimodal.

Reference :
http://scikit-learn.org/dev/auto_examples/preprocessing/plot_power_transformer.html