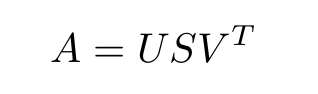SVD (Singular Value Decomposition) - SoojungHong/MachineLearning GitHub Wiki

Singular Value Decomposition

The Singular-Value Decomposition, or SVD for short, is a matrix decomposition method for reducing a matrix to its constituent parts in order to make certain subsequent matrix calculations simpler.

A = U . Sigma . V^T

Where A is the real m x n matrix that we wish to decompose, U is an m x m matrix, Sigma (often represented by the uppercase Greek letter Sigma) is an m x n diagonal matrix, and V^T is the transpose of an n x n matrix where T is a superscript.

The diagonal values in the Sigma matrix are known as the singular values of the original matrix A. The columns of the U matrix are called the left-singular vectors of A, and the columns of V are called the right-singular vectors of A.

Singular Value Decomposition for Dimensonality Reduction

A popular application of SVD is for dimensionality reduction.

Data with a large number of features, such as more features (columns) than observations (rows) may be reduced to a smaller subset of features that are most relevant to the prediction problem.

The result is a matrix with a lower rank that is said to approximate the original matrix.

To do this we can perform an SVD operation on the original data and select the top k largest singular values in Sigma. These columns can be selected from Sigma and the rows selected from V^T.

An approximate B of the original vector A can then be reconstructed. B = U . Sigmak . V^Tk

In natural language processing, this approach can be used on matrices of word occurrences or word frequencies in documents and is called Latent Semantic Analysis or Latent Semantic Indexing.

In practice, we can retain and work with a descriptive subset of the data called T. This is a dense summary of the matrix or a projection.

Singular value decomposition is a method of decomposing a matrix into three other matrices:

Where:

A is an m × n matrix
U is an m × n orthogonal matrix
S is an n × n diagonal matrix
V is an n × n orthogonal matrix

(orthogonal matrix hold condition AA(trans) = A(trans)A = I