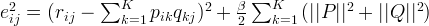Matrix Factorization - SoojungHong/MachineLearning GitHub Wiki
(= Matrix Decomposition) Reference : http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and-implementation-in-python/
Matrix Factorization for Recommender system
Recommendations can be generated by a wide range of algorithms. While user-based or item-based collaborative filtering methods are simple and intuitive, matrix factorization techniques are usually more effective because they allow us to discover the latent features underlying the interactions between users and items. Of course, matrix factorization is simply a mathematical tool for playing around with matrices, and is therefore applicable in many scenarios where one would like to find out something hidden under the data.
Matrix Factorization
Just as its name suggests, matrix factorization is to, obviously, factorize a matrix, i.e. to find out two (or more) matrices such that when you multiply them you will get back the original matrix.
matrix factorization can be used to discover latent features underlying the interactions between two different kinds of entities. (Of course, you can consider more than two kinds of entities and you will be dealing with tensor factorization, which would be more complicated.) And one obvious application is to predict ratings in collaborative filtering.
Example with user and purchased items matrix
In a recommendation system such as Netflix or MovieLens, there is a group of users and a set of items (movies for the above two systems). Given that each users have rated some items in the system, we would like to predict how the users would rate the items that they have not yet rated, such that we can make recommendations to the users. In this case, all the information we have about the existing ratings can be represented in a matrix. Assume now we have 5 users and 10 items, and ratings are integers ranging from 1 to 5, the matrix may look something like this (a hyphen means that the user has not yet rated the movie):
D1 D2 D3 D4
U1 5 3 - 1 U2 4 - - 1 U3 1 1 - 5 U4 1 - - 4 U5 - 1 5 4
Hence, the task of predicting the missing ratings can be considered as filling in the blanks (the hyphens in the matrix) such that the values would be consistent with the existing ratings in the matrix.
The intuition behind using matrix factorization to solve this problem is that there should be some latent features that determine how a user rates an item. For example, two users would give high ratings to a certain movie if they both like the actors/actresses of the movie, or if the movie is an action movie, which is a genre preferred by both users. Hence, if we can discover these latent features, we should be able to predict a rating with respect to a certain user and a certain item, because the features associated with the user should match with the features associated with the item.
Mathematics of Matrix Factorization
Having discussed the intuition behind matrix factorization, we can now go on to work on the mathematics. Firstly, we have a set U of users, and a set D of items. Let \mathbf{R} of size |U| \times |D| be the matrix that contains all the ratings that the users have assigned to the items. Also, we assume that we would like to discover $K$ latent features. Our task, then, is to find two matrics matrices \mathbf{P} (a |U| \times K matrix) and \mathbf{Q} (a |D| \times K matrix) such that their product approximates \mathbf{R}:
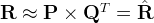
In this way, each row of \mathbf{P} would represent the strength of the associations between a user and the features. Similarly, each row of \mathbf{Q} would represent the strength of the associations between an item and the features. To get the prediction of a rating of an item d_j by u_i, we can calculate the dot product of the two vectors corresponding to u_i and d_j:
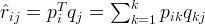
Now, we have to find a way to obtain \mathbf{P} and \mathbf{Q}. One way to approach this problem is the first intialize the two matrices with some values, calculate how `different’ their product is to \mathbf{M}, and then try to minimize this difference iteratively. Such a method is called gradient descent, aiming at finding a local minimum of the difference.
The difference here, usually called the error between the estimated rating and the real rating, can be calculated by the following equation for each user-item pair:
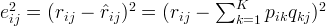
In other words, the new parameter \beta is used to control the magnitudes of the user-feature and item-feature vectors such that P and Q would give a good approximation of R without having to contain large numbers. In practice, \beta is set to some values in the range of 0.02. The new update rules for this squared error can be obtained by a procedure similar to the one described above. The new update rules are as follows.
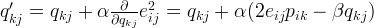
Common extension using regularization