Gradient Descent - SoojungHong/MachineLearning GitHub Wiki
1. Gradient Descent
Gradient Descent is a very generic optimization algorithm capable of finding optimal solutions to a wide range of problems. The general idea of Gradient Descent is to tweak parameters iteratively in order to minimize a cost function.
2. Learning rate
An important parameter in Gradient Descent is the size of the steps, determined by the learning rate hyperparameter. If the learning rate is too small, then the algorithm will have to go through many iterations to converge, which will take a long time
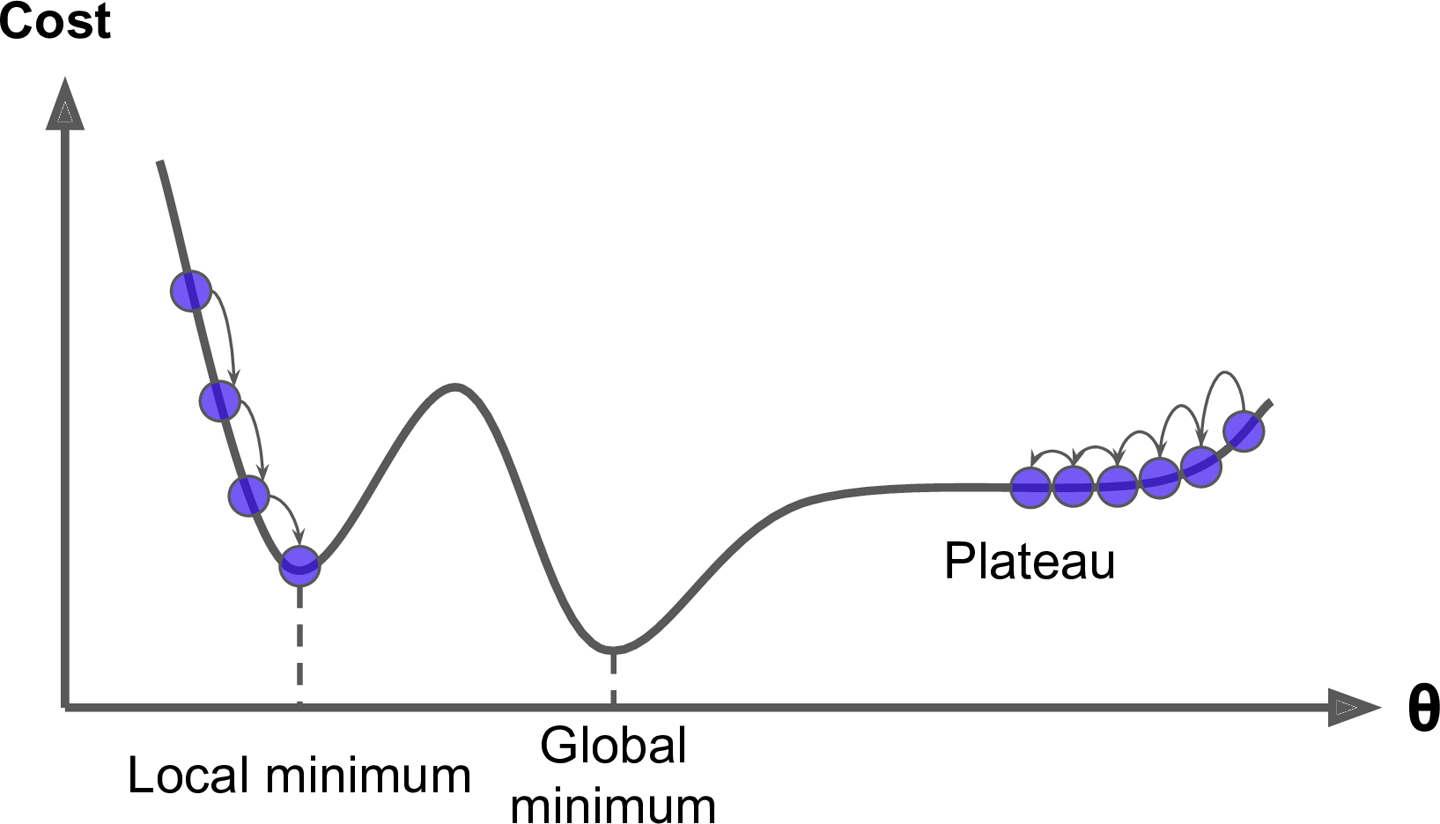
3. Gradient Descent Pitfalls
4. cost function for linear regression is convex function.
Mean Squqre Error is the cost function of linear regression. And this function is convex function.
Fortunately, the MSE cost function for a Linear Regression model happens to be a convex function, which means that if you pick any two points on the curve, the line segment joining them never crosses the curve. This implies that there are no local minima, just one global minimum. It is also a continuous function with a slope that never changes abruptly.4 These two facts have a great consequence: Gradient Descent is guaranteed to approach arbitrarily close the global minimum (if you wait long enough and if the learning rate is not too high).
5. Important warning for Gradient Descent
When using Gradient Descent, you should ensure that all features have a similar scale (e.g., using Scikit-Learn’s StandardScaler class), or else it will take much longer to converge.
6. Partial derivative of the cost function
To implement Gradient Descent, you need to compute the gradient of the cost function with regards to each model parameter θj. In other words, you need to calculate how much the cost function will change if you change θj just a little bit. This is called a partial derivative. It is like asking “what is the slope of the mountain under my feet if I face east?” and then asking the same question facing north (and so on for all other dimensions, if you can imagine a universe with more than three dimensions).
partial derivative of cost function :
7. Batch Gradient Descent :
Instead of computing these partial derivatives individually, you can use Equation 4-6 to compute them all in one go. The gradient vector, noted ∇θMSE(θ), contains all the partial derivatives of the cost function (one for each model parameter).
Gradient vector of cost function :
Notice that this formula involves calculations over the full training set X, at each Gradient Descent step! This is why the algorithm is called Batch Gradient Descent: it uses the whole batch of training data at every step. As a result it is terribly slow on very large training sets (but we will see much faster Gradient Descent algorithms shortly). However, Gradient Descent scales well with the number of features; training a Linear Regression model when there are hundreds of thousands of features is much faster using Gradient Descent than using the Normal Equation.