L05 [Digital Logic II] - Skyline-9/CS2110-Notes GitHub Wiki

L05 [Digital Logic II]

Boolean Simplification Practice

Basically just put everything into this website: https://www.dcode.fr/boolean-expressions-calculator

Gray Code – only one switch per transition

The only version of Gray Code we need to remember is 2-bit

K-Maps

Two adjacent 1s in the map means there is an x + x’ in the formula; the map tells us where

Strategy for 4-variable K-maps

Find a box around 16 1's
- If so, you are done
Find boxes around groups of 8 1's
- If no 1's are left, you are done
Find boxes around groups of 4 1s
- If no 1s are left, you are done
Find boxes around groups of 2 1s
Find boxes around groups of 1
Write a term for every box you drew

You can convert any of these to the other

Truth table
Circuit
K-Maps
Boolean expression

L05 [Digital Logic II]

Sequential Logic vs Cominational Logic

Combinational

Combination of AND, OR, NOT (also NAND and NOR)
Same inputs always produce same output
Analogous to cheap bicycle lock
Examples:
- XOR gate
- ALU
- Multiplexor

Sequential

Requires storage elements
Output depends on inputs plus state
Analogous to a RLR combination lock
Used to build memory & state machines
Order matters
Examples:
- R/S Latch
- Gated D Latch
- State Machine
- LC-3
- Register

Memory

Looking from the outside, we need

Write enable
Memory address
In
Out

Addressability is how many bits are in any one memory location

The addressability of this memory is 8 (8 bits for in and out)

Address space is 4

From the slides, the official definitions are

Address Space -- How many addresses are possible?

Addressability -- How big is each memory location?

Memory Space

Equation: Memory = Address Space * Addressability

Remember that address space is 2^bits

Basic Building Blocks of Memory

Register
- Gated D Latch
Decoder
Multiplexor

Sequential vs Combinational Logic Circuits

Combinational Logic Circuits

Make decisions
Same inputs always produce same output
Depends on what is happening now

Sequential Logic Circuits

Make decisions and store information
Output depends on inputs AND state (can make state machine)
Depends on what has happened in the past (state) as well as what is happening now

A Wrinkle With the D Latch

Problem

A Gated D Latch is a level-triggered device, that is, it will store whatever value is present on the input when the write enable goes from true to false

First, let's introduce what a clock is. A clock is an electrical signal that oscillates between high and low voltage (square waves of 0 and 1). Connect to write-enable of the D-latch to record.

When the clock signal is at its top, the register will output its current inputs. Similarly, when the clock signal goes to zero, the register will record its inputs.

Basically when clock goes to 1, write enable turns on.

When the clock is low

The register is locked when the clock is low, so 7 is passed through the register

When the clock is high

When the clock is high, the register will pass through the values, so 12 will be passed through the register. Problem: we get unexpected results if the output of the device is used in computing the input to the same device

Leader-Follower Flip Flop

Also called a Master/Slave flip flop

Instead of using Gated D-Latches, you would use leader-follower flip flops (d-flip flop or register in Circuitsim)

9/14/2021 Attendance Quiz

Today's Number: 82,200

Question #1: Level-triggered sequential circuits can yield unexpected results if

D. The output of the device is used in computing the input to the same device

The improvement is edge-triggered (locked on the clock edges instead of the level dropping). Remember level-trigger is just a regular D-latch

Question #2: How many bits of storage are we going to need for the garage door opener state machine?

Question #3: With three inputs and three state bits, how many lines would the truth table require if it didn't contain "don't care" entries?

Finite State Machine

With combinational logic and sequential logic (storage elements), we can start building finite state machines

Example

We have a button that we want to open and close the garage door when we press the button. More specifically,

When the garage door is down and we press the button, we open the door
When the garage door is up and we press the button, we close the door

Note: every time you make a clock tick, you have to transition to a state, even if you transition to yourself

What keeps you in the same state? What happens if you just hold down the pushbutton?

To solve this, we introduce a dummy state when the button is held down

There are two types of state machines

One Hot	Binary Encoded
One bit per state	Encode state as a binary number
Only one bit is on at a time	Use a decoder to generate a line for each state
Faster	Slower
Requires more flip-flops	More complicated
00001»00010»00100»01000»10000	000»001»010»011»100

L06 [Von Neumann Model]

Harvard Model

They stored data and programs separately

Von Neumann

Stored data and program together in the same memory

Pros

Less circuits

Cons

Can mix up data and program
Program can change all the program data as well

The Von Neumann model leads us to treat machine instructions just as another data representation

Big deal!!

Think of

Unsigned integers
IEEE-754 floating point numbers
...
Machine Instructions

They are all just bits!

Introducing the LC-3 CPU

Address Space	Addressability	Architecture	General purpose registers	Instruction size
`2^16 = 65536`	`16 bits`	Von Neumann	`8`	`16`

Address space for modern 64-bit computers is 2^64, though in practice the memory is limited by the CPU, the memory controller, or the printed circuit board design

Series of 16-bit numbers becomes your program instructions! Yay :D

The slashes on the wires just means how many wires are chained together

Tri-state buffer

The tri-state buffers are used to help with the bus

The bus is 16 shared wires in the datapath
This is what is used to disconnect inputs so the bus can be shared among multiple components

A triangle is just a buffer

Add a bubble and it becomes a not gate
Buffer by itself does nothing, 1 goes in 1 goes out and 0 goes in and 0 goes out

Patt names all his tri-state buffers with the prefix “gate”

Remember – our logic gates literally connect their output to +VCC for 1 and Ground for 0

When sharing a wire with another circuit – this arrangement is called a bus
What happens when you connect a 1 (+VCC) to a 0 (ground)? You short circuit

Z means floating high impedance (wire is basically cut off, we don't know the voltage)

Tri-state buffers are bit more complicated than transitors because you have to pass both a 1 and a 0 to the output

If my address space is 8, I need 3 wires (2^3)

Register File Circuit

A small, fast "Memory"
- Address space: 8 registers
- 16-bit addressability per reg
The single /16 on the top represents data in
Two outputs
- Dual ported memory
- Can read two regs at same time
- Source Register 1 (SR1) [3 bit address]
- Source Register 2 (SR2) [3 bit address]
One input
- DR (3 bit address)
  - Chooses which register to write into
- LD.REG (write enable)

Property of Leader-follower flip-flop: you can read a value in and write a value out at the same time

Categories of Machine Instructions

Operate (ALU)

Data Movement

Load
- LD
- LDR
- LDI
- LEA
Store
- ST
- STR
- STI

Control

BR
JMP
JSR
JSRR
RET
RTI
TRAP

How do we make the LC-3 do an “ADD”?

The LC-3 is controlled by a large finite state machine.

So it has output signals (control signals)

Like UP and DOWN signals in the garage door

The FSM turns on specific control signals in the LC-3

This activates certain paths in the datapath.
These control signals can make the datapath do things, such as add two numbers (R1 and R3), and store the result in R2.

Participation Quiz 9/16/2021

Today's number is 30,900

Tri-state buffers are used to

Prevent data path fires
Avoid short circuits
Disconnect a circuit from a bus so that another circuit can assert a value on the same bus without interference
Present a value that is neither a 1 or 0 on an output

The Program Counter (PC) register holds

The address of the next instruction to be executed

The Instruction Register (IR) holds

The instruction currently being executed

Recitation 9/15

Sequential Logic

Output depends on previous output and input

R/S Latch (Reset/Set Latch)

Stores one bit

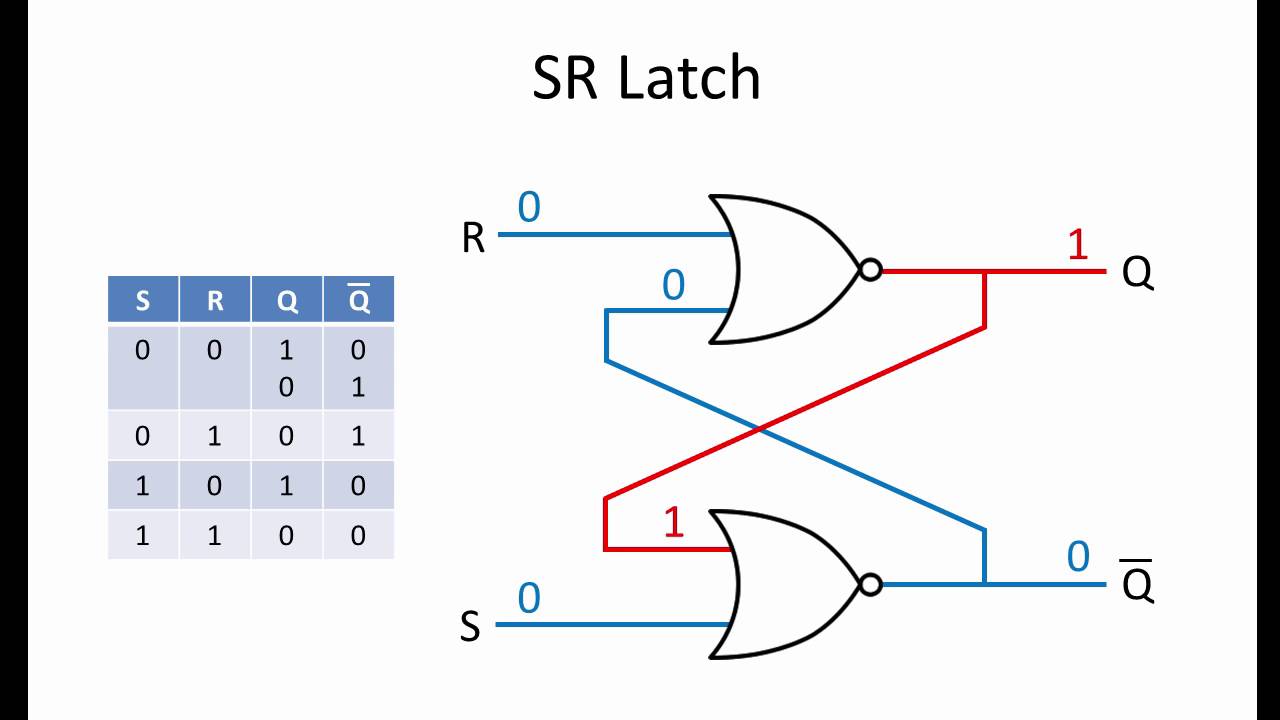
R	S	Out	!Out
0	0	X	X
0	1	0	1
1	0	1	0
1	1	0	0

When at R = 1, S = 1, the output at this state depends on the previous state (moldy state)

Gated D-Latch

Gated D-Latches are basically just an RS-Latch with extra control

Can choose when to save the output and what to save it as

Level-triggered Logic

In level-triggered logic, the output can only change when the enable bit is 1
When the enable bit is set to 0, then the output is unaffected by changes in the input

Edge-Triggered Logic

Rising-edge triggered logic: The output can only change when the clock changes from 0 to 1
Falling-edge triggered logic: The output can only change when the clock changes from 1 to 0

D-Flip Flops

Left D-latch updates when the clock is 0, and the right D-latch updates when it is 1

It's kinda like an air lock for a space station

To get out, you open the air lock, close it, then open the outer door
To get in, open the outer door, close the outer door, then open the air lock

Registers

Essentially the same as a D Flip-Flop, but there are n-bit input or output lines instead of just one

State Machines

Dave has 3 possible states

Dancing (requires 3 charges)
Charging with 1 charge
Charging with 2 charges

Address Space & Addressability

Computer memory is made up of distinct memory addresses, each containing some amount of data

Addressability: the amount of data stored at any given memory address

Address space: An n-bit address line can represent 2n memory addresses