L03 [Datatypes II]

Outline

• Logical Operation on Bits
  • AND, OR, NOT, XOR (NAND, NOR)
  • Shift
• Other Representation
  • Bit vectors
  • Hex
  • Octal
  • ASCII
  • Floating Point

Bitwise AND

Pog look at this big brain truth table

A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

AND is also denoted as &

Bitwise OR

Pog look at this big brain truth table

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

OR is also denoted as |

Example Find 0101 OR 0110

Answer: 0111 or 7

Bitwise NOT

Also called a complement

A	~A
0	1
1	0

Boringest truth table

XOR

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

Application of XOR: used to find overflow for the carry in and carry out

Also symbolized with ^ in C, C++, Java, and some others

Bitwise NAND

Just do an AND and flip all the bits

A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

Bitwise NOR

Just do an OR and flip all the bits

A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

Left Shift

Just move all the bits to the left

0110 leftshift 10 a.k.a. 7 << 2

Answer: 1000

Right Shift

Just move all the bits to the right

0110 rightshift 10 a.k.a. 7 >> 2

Answer: 0001

Note Well If you right shift with Two's Complement, you fill it in with sign extension (arithmetic right shift)

1101 rightshift 10 a.ka. 13 >> 2

After: 1111

Boolean Masking

Often, we use a constant (boolean mask) with a boolean function

1. Clear

Identity: xyz & 111

• To clear, put a 0 in the bit positions you want to clear (e.g. 101 clears bit position 2)

2. Set

Identity: xyz | 000

• To set, put a 1 in the bit positions you want to set (e.g. 010 puts a 1 in bit position 2)

3. Toggle

Identity: wxyz ^ 0000

• Put a one in any bit you want to toggle
• Example: 10101 ^ 10000 == 00101

Misc info about masking

1. To test a bit, clear all the rest

wxyz & 0010 == 00y0

Now you can test 00y0 == 0000

2. To put a 1 in any position n of a mask, left shift by n 1 << 2 == 0100

3. To put a zero in position in a mask, put a one in that position and complement

~(1 << 2) == 1011

• Creates as many leading 1s as you need

Recitation Notes

Base Conversions

1. Split each digit up
2. Convert each digit to 3 (for octal) or 4 (for hex) bit binary
3. Combine each binary number

Bases

There is a problem using binary because it's rather difficult to examine long binary strings, and so writing/reading long binary strings is prone to error. To solve that, we often represent binary in a base that's a power of 2

1. Octal (Base 8)
2. Hexadecimal (Base 16)

Octal is just 2^3 so just group binary strings into groups of 3, while Hexadecimal is just 2^4 so just group binary strings into groups of 4

Notations for bases

• 456 for decimal
• 0456 for octal
• 0x456 for hexadecimal

ASCII

Fun facts

• To convert between upper case and lower case, add/subtract 0x20 or toggle the 5th bit

Floating Point Representation

IEEE-754 standard

Rememeber that the exponent is offset by 127 and the mantissa is normalized (meaning that it starts with 1.xxx)!

• The reason why the mantissa is normalized is because otherwise you can represent the same number multiple times
  • Ex: 0.123 * 10^2 = 1.23 * 10

For example, to get 2^0 or 1, you have to set 127 in the exponent area because it's offset by 127.

Special Cases

	E ==0	0 < E < 255	E == 255
M == 0	0	Powers of 2	∞
M != 0	Non-normalized, typically underflow	Ordinary old numbers	NaN

Mathematically 0 is represented with by 0 and -0 (so the sign bit doesn't matter)

∞ and -∞ are also represented with toggling the sign bit

Why do we not use 2's complement for the mantissa?

• It's so it's easier to compare IEEE-754 numbers without having to do 2's complement exponent comparison
  • In particular we can actually compare IEEE-754 numbers the same way we compare 2's complement numbers

Recitation 9/1

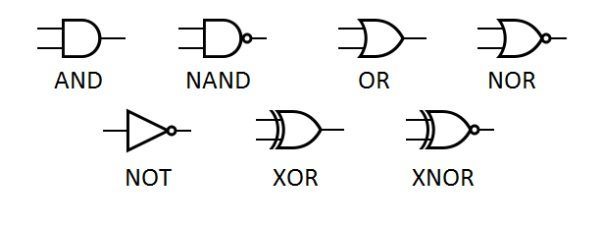
Logic Gates

Datatypes II (cont)

Special Cases for Floating Point Number

	E ==0	0 < E < 255	E == 255
M == 0	0	Powers of 2	∞
M != 0	Non-normalized, typically underflow	Ordinary old numbers	NaN

NaN Quirkiness Suppose A is a floating point number set to NaN

• A != B is true for any value of B
• A != A is true as well
• Basically, A compared to anything will only return false

Underflow Edge case for tiny numbers: E == 0 is special, so 2^-126 is smallest exponent; we use underflow case for anything smaller, like 2^-127; note E==0 is computed as E==1

For example, 0 00000000 10000000000000000000000 = 2^-127

And so the smallest possible number is 0 00000000 00000000000000000000001 = 2^-149

FP Comparison

IEE-574 allows us to perform certain comparisons with no conversion

For example,

3.67 x 10^14 = 0x57a841ab
2.89 x 10^16 = 0x5acd58cb

Notice the exponent bits come first in the representation, so an integer comparison can work if the numbers are the same sign

Note: Negative floating point number in hex will have the first digit > 7

Comparing Two FP Numbers

1. If either is NaN, the comparison is defined as “unordered” (all comparisons to it except != are false)
2. If either is -0.0, replace with 0.0
3. If the signs (high bit) are different, the positive number is bigger
4. Compare the rest of the bits as integers
5. If the signs are both negative reverse the comparison

What do you need to know?

Given the 6-case chart of FP numbers, be able to

• Know what each case means and recognize FP numbers that fit that case
• Know that in the 32-bit form the exponent is biased by -127
• From an encoded 32 bit number, be able to show its value in the form of M * 2^E
• Be able to compare FP numbers for <, >, == !=

Understand

• Converting decimal FP to IEEE-754 and vice versa
• Precision issues in converting between integer and FP representations

Bitwise Questions

Why is x = x & ~077 better than x = x & 0177700?

Answer: x = x & ~077 clears the last 6 bits for any arbitrary length, not just 16 bits

What does x >> (p + 1 - n)) & ~(~0 << n) do?

This is basically getting n bits from position p

Digital Logic

Transitors

n-Type transitor is normally open, p-Type transitor is normally closed

You open the gate by applying current to the gate

Common Misconceptions

• Wire with +2.9 volts is logical 1
• Wire with 0 volts can represent logical 0
• Wire that is not connected is said to be floating or in high impedance and its value can randomly vary from a logical 0 to 1

You have to be connected to be connected to some potential if you are a 1 or a 0

Logical Gates

Attendance Quiz #1

1. What is today's number? 16384 or 2^14

2. We’re using 32-bit unsigned binary representation for integers; what value would result from (12 | 7) ^ 63

12 in binary is 0000 1100

7 in binary is 0000 0111

12 | 7 is 0000 1111

63 in binary is 0011 1111

0000 1111 ^ 0011 1111 is 0011 0000

32 + 16 = 48

3. You are given a 16-bit unsigned binary number, x. To test if bit 8 (numbered from right to left starting at 0) is 1, you could use

x & (1 << 8) != 0

4. What number is represented by this 32-bit IEEE-754 encoding? 0 10001110 00000000000000000000000

2 + 4 + 8 + 128 - 127 = 15
2^15 = 32768