Tree (Java) - ShuweiLeung/Thinking GitHub Wiki
1.(617:Easy)Merge Two Binary Trees
- 该题是一个非常典型的遍历树结构的题目,使用递归调用,维护一个pre指针指向当前处理结点的父节点。以t1树作为主要参照物来cover t2树,当t1为null时,直接让pre的左右子树指针指向t2结点及其子树;若t2树为null,则直接返回即可,因为pre指向的就是t1树。若t1、t2均不为null,则更新t1当前结点的val值,然后更新pre指针,继续递归遍历t1、t2的左右子树即可。
2.(669:Easy)(非常经典题)Trim a Binary Search Tree
- 题目关键点binary search tree(二叉排序树),即若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
- 所以,若当前节点的值小于L时,那么父节点应指向当前结点的右子树;若当前结点的值大于R时,父节点应指向当前结点的左子树;若当前结点的值在L和R之间,则当前结点作为它左右子树的父节点进行左右子树的递归搜索。
3.(637:Easy)(非常经典题)Average of Levels in Binary Tree
- 该题除了广度优先搜索遍历。我们在遍历每层的结点时,还可以向递归搜索函数传入一个level层数参数来标记将遍历的结点所在层数,用HashMap保存某一层结点的各个值(key为层数,value是一个ArrayList列表,存储key层的结点的值)。最后按照key的大小再遍历一遍hashmap取出每层结点的值求得结果即可。
- 当然上面的思路并没有直接使用广度优先搜索的效率BFS高。我们每次将当前层的结点的子结点加入队列时,都会先读取当前队列的长度,即当前层的结点总数,然后用for循环遍历时,控制i<n即前n个结点,从而保证每次循环处理的都是同一层的结点。
4.(104:Easy)(非常经典题)Maximum Depth of Binary Tree
- 该题使用BFS广度优先搜索遍历即可获得最大深度,初始化最大深度变量maxDepth=0,每当队列不为空,说明当前层有结点,则将maxDepth加1。
- 该题也可以进行递归搜索,即DFS深度优先搜索遍历,取左子树和右子树深度的最大值,然后加1(算上该层)返回上一层,该思路效率会更高。
5.(226:Easy)(经典题)Invert Binary Tree
- 该题和交换两个变量的值的思路类似,只不过需要递归处理左右子树而已。需要用一个临时变量存储左子树,然后使当前结点的左指针指向右子树,而右指针指向临时变量。然后递归的处理当前结点的左右子树即可。
6.(653:Easy)(非常经典题)Two Sum IV - Input is a BST
- 该题只需要设立一个Hash表存储目标需要元素值即可,即target = 10,当前node结点的val值为3,则在hash表中存入10 - 3 = 7,那么当某一个结点的val值为7时,说明树中存在某一个结点可以与当前结点配对,返回true。
7.(538:Easy)(非常经典题)Convert BST to Greater Tree
- 该题一种方法是,先遍历所有的结点并将每个结点的val值保存到list中并升序排序,然后第二次遍历树,用indexOf()在list中找到当前结点的值,并将当前结点的val值更新为greater node。
- 此外,因为是二叉排序树,所以所有比当前结点的val值大的结点都在右子树上,为了遍历更新所有的结点,我们采用逆中序遍历的顺序,先遍历所有右子树,得到右子树的所有结点值之和,也是所有比当前结点的val值大的结点值之和,然后再遍历左子树。我们用sum值存储所有比当前结点值大的其他所有结点的val值之和,包括当前结点的右子树结点,和当前结点的上层父结点和曾祖父结点以及它们的右子树等等。
8.(100:Easy)(非常经典题)Same Tree
- 一种方法是根据第一个树使用中序遍历存储到list中,然后再依照完成的中序遍历list顺序对比第二个树。这里可以每验证完一个结点,就从list中将当前头结点删除来确保同步。
- 另一种方法是按照相同的搜索顺序同时进行递归搜索DFS对比,代码很简洁,思路如下:
public boolean isSameTree(TreeNode p, TreeNode q) { if(p == null && q == null) return true; if(p == null || q == null) return false; if(p.val == q.val) return isSameTree(p.left, q.left) && isSameTree(p.right, q.right); return false; }
9.(404:Easy)Sum of Left Leaves
- 该题只需求和左子树的左叶子节点值即可,可以用一个方向参数来指示当前递归的是否是左子树。
- 注意:求和的一定是叶子,而不能是中间节点!
10.(563:Easy)(非常经典题,尤其笔记第二点)Binary Tree Tilt
- 该题要理解题意:absolute difference between the sum of all left subtree node values and the sum of all right subtree node values。注意这里的当前搜索到的根节点也要算进去,它也算父节点的子树中的节点。
- Java中,我们可以通过一个成员变量实现值的共享同步,类似于ArrayList中,以该题的代码为例来理解:
public class _563_BinaryTreeTilt { int result = 0; //通过一个成员变量实现值的共享同步 public int findTilt(TreeNode root) { postOrder(root); return result; } private int postOrder(TreeNode root) { if (root == null) return 0; int left = postOrder(root.left); int right = postOrder(root.right); result += Math.abs(left - right); return left + right + root.val; } }
11.(108:Easy)(经典题)Convert Sorted Array to Binary Search Tree
- 该题要求每个树和子树都是一个平衡树,所以我们需要递归的找中点,即先在nums数组中找到中点,然后再以nums数组的中点为分界线找左半部分数组的中点和右半部分数组的中点,然后递归的去建立。找中点的公式可以为:(start + end) / 2,start和end是当前数组开始和结束索引。
12.(543:Easy)(非常经典题)Diameter of Binary Tree
- 该题需要比较每一个子树左右深度之和,而不能只比较根节点的左右子树深度之和,因为有一个test case的答案最长路径存在于根节点的右子树中,而不是以根节点为根的树中。
- 此外,吸取第10题(563)的经验,我们用一个成员变量maxDepth来进行全局同步,比较递归过程中每一个子树的左右深度之和并取最大值。
13.(107:Easy)Binary Tree Level Order Traversal II
- 该题只需借用HashMap,key为深度,value为该深度下的结点val值集合,dfs建立好HashMap后,根据key值逆序建立返回列表即可。
14.(671:Easy)Second Minimum Node In a Binary Tree
- 该题只需要设立两个变量分别代表“最小值”和“次小值”即可,在dfs递归搜索的过程中依次与这两个值比较。当搜索的当前结点val值小于等于“最小值”时,才有必要递归搜索它的左右子树,因为虽然左右子树比该结点val值大,但可能比当前的“次小值”小;而当当前的结点val值大于“最小值”,无论它是否比“次小值”小,都没必要继续搜索它的左右子树,因为该结点的左右子树结点值一定大于等于该结点值,所以一定是第三小、第四小...的数,不必再递归搜索。
15.(257:Easy)Binary Tree Paths
- 该题只是一个简单的DFS深度优先搜索遍历。此外只需要注意,寻找的是一条从根到叶子结点的路径,叶子结点的左右子树均为null。
16.(101:Easy)(经典题)Symmetric Tree
- 该题只用中序遍历树即可,但要在遍历的同时也要对空节点作标记。而且,我们还要记录每一个结点的深度,为了保证是同一深度的结点对称,否则无法通过所有测试例。具体的实现思路可以参看代码实现。
- 上面的方法很愚蠢,直接看下面的代码思路:
public boolean isSymmetric(TreeNode root) {
if(root==null) return true;
return isMirror(root.left,root.right);
}
public boolean isMirror(TreeNode p, TreeNode q) {
if(p==null && q==null) return true;
if(p==null || q==null) return false;
return (p.val==q.val) && isMirror(p.left,q.right) && isMirror(p.right,q.left);
}
17.(572:Easy)(经典题)Subtree of Another Tree
- 该题s树是参照物,我们递归搜索s树,查找s树中与t树的根节点匹配的结点,然后比较他们的子树是否匹配。若s树中当前结点与t树根节点不匹配,则查看s树当前节点的左右子树中是否有与t树根节点匹配的结点。
- 具体思路看代码实现,beat 91%。
18.(110:Easy)Balanced Binary Tree
- 该题只需要记录每个结点左右子树的深度,然后作差比较即可。用一个成员变量作为全局变量,来表示目前遍历的所有子树是否均是平衡二叉树。
19.(112:Easy)Path Sum
- 该题比较简单,只需要在递归到叶子结点时比较当前的搜索路径的val值之和是否等于sum即可。
20.(437:Easy)(非常经典题)Path Sum III
- 该题的难度在于"如何变换路径搜索的起点且保持路径上结点值之和同步"。我们可以递归的调用"主函数",并且传入当前结点的左右孩子来更改路径的起点位置。然后就可以按照Path Sum一中的递归传值来判断是否路径val和为sum。参考的代码如下:
public int pathSum(TreeNode root, int sum) { if(root == null) return 0; return findPath(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum); //注意pathSum是变换路径的起点,findPath是以传入结点为起点进行搜索 } public int findPath(TreeNode root, int sum){ //以root为起点的向下搜索路径,sum值与主函数中的sum值不同,是剩余结点和应等于的sum值 int res = 0; if(root == null) return res; if(sum == root.val) res++; res += findPath(root.left, sum - root.val); //剩余结点值的和应为sum-root.val res += findPath(root.right, sum - root.val); return res; }
该题好像还有利用prefix来求解的方法,更高效,下次复习时参考discuss学习
21.(235:Easy)(非常经典题)Lowest Common Ancestor of a Binary Search Tree
- 该题一定要注意到题目中的关键字"Binary Search Tree"(二叉排序树),所以我们可以直接根据二叉排序树的性质求得答案。假设p、q结点的值为p<q,当当前遍历的结点node.val < p时,那么Lowest Common Ancestor一定在node的右子树中;当node.val > q时,那么Lowest Common Ancestor一定在node的左子树中,当p < node.val < q时,当前结点node就是Lowest Common Ancestor。(见代码实现1)
- 对于更一般的没有特殊性质的二叉树,我们可以递归搜索整个树,统计以某个结点为起点的路径上是否包含p、q结点,若均包含,则在LCA指针为null的情况下当前结点就是Lowest Common Ancestor,否则Lowest Common Ancestor一定在深度更低的下层某个结点上;若只包含其一或者一个都不包含,则Lowest Common Ancestor一定在上层结点上,最糟糕的情况是整个树的根节点。(见代码实现2)
22.(501:Easy)(经典题)Find Mode in Binary Search Tree
- 该题我是用了HashMap来统计每一个结点val值的频率,最后取频率最高的val值加入返回数组中。
上面的方法只beat33%,discuss中应还有更高效的方法,不借助额外空间,下次复习时应该再研究
23.(111:Easy)Minimum Depth of Binary Tree
- 该题只是一个简单的DFS问题,当遍历的结点是叶子时返回当前叶子的深度,否则取左右子树中深度较小值返回即可,具体思路可参看代码实现。
24.(687:Easy)(非常非常经典题)Longest Univalue Path
- 该题其实有点像第20题(437),但实现方法并不完全相同。该题关键点是需要分为三种情况来考虑(beat 97.86),示意图分别如下:
第一种情况:
该情况比较容易想到,一条相同值的路径就是一条由上通往下层的路径。
2
|
2
/ \
2 3
第二种情况:
该连续路径是一条折线段,所以我们需要比较分叉点左右两侧相同路径的长度,并把左右的长度加起来。
该情况需要注意:
1、交叉点为pathLen = 1的中间结点,我们在比较它左右两侧的值时,需要让交叉点左右两侧返回的leftLen和rightLen减去当前的pathLen(1),
因为折现段并不包含第一个pathLen = 0的树根节点
2、交叉点在向上层返回值的时候,应取leftLen和rightLen中的较大值
2 pathLen = 0
|
2 pathLen = 1
/ \
2 2 pathLen = 2
\
2 pathLen = 3
第三种情况:并不是针对路径长度,而是针对返回值
对于pathLen = 2的val值为1的中间节点,它向上层返回时,应返回0,但由于pre结点(pathLen = 1的结点)在比较折线段长度时会减去它的
pathLen(1),所以并不影响;当前层的pathLen-1(1)与上一层的pathLen(1)相等,所以也不影响返回值(Max(leftLen, rightLen))。
2 pathLen = 0
|
2 pathLen = 1
/ \
2 1 pathLen = 2
\
1 pathLen = 1
25.(814:Medium)Binary Tree Pruning
- 该题很简单,只需要递归的判断左右子树是否不含1即可。具体思路参看代码实现。
26.(654:Medium)Maximum Binary Tree
- 该题很简单,维护一个max最大值变量和index最大值索引即可。递归建树,具体思路参看代码实现。
27.(513:Medium)Find Bottom Left Tree Value
- 维护两个全局变量leftmostVal和leftmostLayer,分别存储最左侧结点值和对应的深度,当我们便利到当前的左侧结点值时,若它比之前的左侧结点还深,则更新对应的leftmostVal和leftmostLayer变量。
28.(515:Medium)(经典题)Find Largest Value in Each Tree Row
- 该题是一个非常典型的BFS广度优先搜索题目。需要注意的是,test case中会存在负数,且最后一个test case测试例是int型的最小值-2147483648,所以需要关注更新策略,将
val > max改为val >= max。
29.(508:Medium)(经典题)Most Frequent Subtree Sum
- 题目中文翻译:给出一个树的根节点,要求你找到出现最频繁的子树和。一个节点的子树和是指其所有子节点以及子节点的子节点的值之和(包含节点本身)。所以最频繁的子树和是什么?如果有并列的,返回所有最高频率的值,顺序不限。
- 首先在确保已经理解题意的基础上,我们要求得所有子树的结点值之和,且用一个HashMap统计他们出现的频率(key为subtree sum,value为对应出现的频率),最后取频率最高的subtree sum返回即可。
30.(94:Medium)(非常经典题)Binary Tree Inorder Traversal
- 该题是对树遍历的最简单的一个应用,通常用递归的方法解决比较简单易理解,且在该题的test case中用递归求解可beat 90%+。
- 此外,也可以使用迭代循环的解法,用stack来保存之前访问过的路径即可,具体可以参看代码实现,但该思路只beat 44%。
需要掌握循环迭代解法,下次复习时要再温习
31.(655:Medium)(非常经典题)Print Binary Tree
- 该题首先要明确题意,每一层的树根结点均在它那一数组部分的中间位置。此外,我们可以用递归方法求解出树的高度,而对于返回数组每一行的长度,我们通过examples可以发现,对于高度为h的树,数组每一行的长度为2^h-1。
- 在明确以上几点内容后,我们可以用递归的方法在返回数组中填充整个树,具体思路可以参看代码实现。(beat 98%)
参考视频:中文视频教程
32.(144:Medium)(非常经典题)Binary Tree Preorder Traversal
- 该题和第30题(94)一样,可以用递归和循环迭代两种方法,但是递归的效率会更高一些(beat 98%),且更易懂。
需要掌握循环迭代解法,下次复习时要再温习
33.(623:Medium)Add One Row to Tree
- 该题还是BFS广度优先搜索遍历的一个简单应用,当找到d-1层以后,便可以按题目要求来新增一层子结点,具体实现请参考代码实现,思路简单清晰。
34.(230:Medium)(非常非常经典题)Kth Smallest Element in a BST
- 该题是一道非常好的题目,一种方法当然是忽略二叉排序树的性质,暴力求解,用一个ArrayList列表来维护最小的k个元素值,然后不断更新它,最后返回这个列表的首元素,但该思路效率极低(因为没有用二叉排序树的性质),只beat 4%。
- 第二种方法是灵活运用二叉排序树的性质求解,因为中序遍历的顺序是先左子树、根节点、右子树,正好在二叉排序树中是值递增的顺序,所以我们只需要从整个树的最左叶子开始,用中序遍历不断回溯递归,当计数器的值为k时,当前结点值就是答案,具体实现思路见代码。
该题第二种思路除了上面的一种思考方式外,还有其他实现解法,下次复习时应该参看学习
<35>.(337:Medium)(非常非常非常经典题)House Robber III
- 该题其实是动态规划题目,需要维护两个状态变量,偷这个叶子结点房子和不偷这个叶子结点房子。如果偷当前结点房子,则相邻房子不能偷;如果不偷当前房子,则相邻房子可以偷也可以不偷,因为要获取最多偷的钱,所以取相邻房子偷或不偷的最大值。整个实现思路是bottom-up的,即由下到上的。
非常非常好的参考视频教程:House I/II/III动态规划问题全解析
36.(684:Medium)(非常非常经典题)Redundant Connection
- 该题其实本质是判断给定的两个结点是否在同一个连通分量中,如果不在同一个连通分量中,则将两节点所在集合合并为一个集合(连通分量);否则,连接当前两个结点的边就是多余的。
- 处理上述图论连通分量的问题通常使用Union-Find方法,用一个roots数组保存每个结点的父结点,下标索引代表结点值。当下标索引i和roots数组对应位置上的roots[i]相等时,该结点值为i的结点就是它所在连通分量的根。那么Find操作就是给定一个结点x,向上回溯寻找某个结点i,满足roots[i]=i,该结点i就是x的根节点。对于Union操作,给定两个结点x和y,它们的根节点分别为i1和i2,那么union就是执行roots[i1]=i2的操作,使i1和i2代表的两个连通分量合并。
感觉该题是图论graph题,而不是一个tree题
37.(173:Medium)(非常经典题)Binary Search Tree Iterator
- 该题本质上就是将整个树的结点值按从小到大排序,然后每次调用next()函数,都返回当前最小的结点值并将其在顺序集合中删去,直到为空。
- 一个非常简单的解决办法是在初始化迭代器类时,遍历这棵二叉树,把二叉树的元素以从大到小的方式放到一个栈里,这样next()从栈顶获取元素,hasNext()调用栈不为空的判定方法。这种方法能满足题目中的时间复杂度要求,但是空间复杂度无法满足题目中O(h)空间复杂度要求。
- 正确的解法是:我们维护一个栈,暂且称之为最小元素栈,栈中存放的是结点指针,向栈中添加元素发生在两种情况下:1.初始化迭代器时;2.调用next()从栈中弹出一个元素时。我们结合下面的实例来描述这个栈中元素的添加和删除过程。对于hasNext()方法,调用栈的empty()方法即可,不做具体分析,仅分析next()方法以及迭代器的数据结构。
假设二叉查找树的结构如下:
6
/ \
5 8
/ / \
1 7 9
\
3
/ \
2 4
(1)栈的初始化,我们把root一直到最左下角的结点都放到stack中,即把如下三个结点放在stack中。
6 | |
/ | |
5 | 1 |
/ | 5 |
1 |_6_| <---栈内情况
注意:上图中栈中存放的应该是指针而不是1,5,6等元素,此处仅用作示意,不代表实际情况,请勿生疑。
(2)第一次调用next(),此时弹出指向元素1的指针tmp,这时候栈内只剩下5,6,如果我们不对栈进行维护的话,我们再调用一次next()将会弹出5,这显然是不对的,因为二叉查找树中还有比5小比1大的元素。因此这时候,我们应当将二叉查找树,或者更准确的说,应该把元素1的右子树上的部分结点添加到栈中。
| |
| |
| |
| 5 |
|_6_| <---栈内情况
(3)那么我们将1(tmp)的右子树上所有结点都放到栈内吗?不,此时添加结点的逻辑与初始化迭代器时类似, 我们只把从tmp->right为根一直到其最坐下角的结点都放到stack中,即,把3,2两个元素放到栈中。
| |
| 2 |
| 3 |
| 5 |
|_6_| <---栈内情况
(4)再次调用next()时,返回的将是正确的答案2,然后2并没有右结点,则无须添加新的指针到栈中。
| |
| |
| 3 |
| 5 |
|_6_| <---栈内情况
(5)之后的过程与此类似,在此把每次调用next()之后的栈的存储情况列举如下:
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| 4 | --> | | --> | | --> | | --> | | --> | | --> | |
| 5 | | 5 | | | | 7 | | | | | | |
|_6_| |_6_| |_6_| |_8_| |_8_| |_9_| |___|
- 综上所述,我们在栈中存储的是一部分极小值,且栈顶一定是当前树中未访问过的结点中的最小结点。在调用next()弹出最小结点时,需要把被弹出结点的右子树添加到栈中,也就是把比当前最小结点大但是比次小结点小的那些结点中的一部分(不是全部,只是被弹出结点右子树根节点的左孩子分支上的结点,即已弹出结点的相邻较大值)添加到栈中。
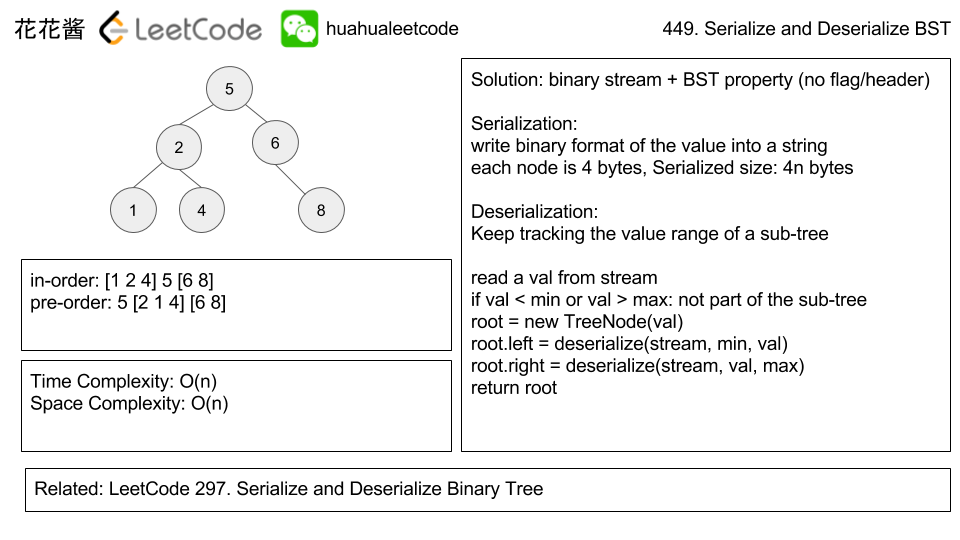
38.(449:Medium)(非常非常经典题)Serialize and Deserialize BST
- 一种思路是使用BFS,把所有空节点保存成null,对于非BST应该是唯一做法。但是,BST只需要保存前序遍历就可以,不保存中序和后序遍历是因为给一个遍历序列而没有其他信息找不到树或子树的根节点。
- 以上图为例,对于前序遍历,5[2 1 4][6 8],因为对于BST的根节点来说,其左子树所有结点的值都小于根节点,而右子树所有结点的值都大于根结点,因此,我们在反序列化建树时,根据下一个位置的值预判出是左子树或右子树,则只需要限制其最小值和最大值即可。具体实现请参看代码实现。
参考视频:参考中文视频教程
39.(102:Medium)Binary Tree Level Order Traversal
- 该题就是简单的BFS求解,没有什么难度。
40.(199:Medium)(经典题)Binary Tree Right Side View
- 该题其实也是一个BFS广度优先搜索遍历的例子。
- 该题一开始想用DFS求解,从根结点开始,优先选择搜索右子树,当右子树不存在的时候才选择搜索左子树,但这种思路有一个问题,如下例所示:
5
/ \
3 2
/
6
如果按照上面DFS思路,结果是5->2(因为2没有左右子树,递归被迫停止),但正确答案却是5->2->6。
- 因此,正确思路应该是使用BFS,取每层最右侧的结点值加入结果集,具体思路细节参看代码实现。
41.(96:Medium)(非常经典题)Unique Binary Search Trees
- 该题有两种解法,我是用的递归思想,但效率较低,beat 0%。思路是:对于结点为n的一棵树,除了一个结点作为根结点,其余的n-1个结点可以全在根节点的左子树或右子树上,也可以分布于根节点的两侧。对于根节点的左右子树的根节点,也是同样的思路,除去子树根结点,剩余结点既可以在子树结点的一侧,也可以分布于两侧。因此我们便可以写出递归方程,如下:
public int numTrees(int n) {
if(n == 1)
return 1;
int res = 0;
//结点全在一侧
res += numTrees(n-1) * 2;
//结点在两侧
for(int i = 1; i <= n-2; i++) {
res += numTrees(i)*numTrees(n-i-1);
}
return res;
}
- 第二种更高效的解法是动态规划思想,其实与递归方法的分析一样(其实两种解法本质上是一样的,只是递归更耗费时间,用到堆栈,而DP可以一次存取),假如我们现在要求n个结点的unique trees数量dp[n],那么相对于n-1个结点的unique trees来说,我们把多出来的第n个结点作为新树的树根,那么如果n-1个结点全部都在树根的一侧,则我们只需要在n-1个结点的unique trees之上加一个新的根结点即可;当n-1个结点分布于两侧,则新树的情况为dp[左结点数]*dp[右结点数]即:
第n个结点
/
n-1个结点的所有unique trees情况
此时产生的新树有dp[n-1]个
第n个结点
/ \
j个结点的所有unique trees情况 n-j-1个结点的所有unique trees情况
此时产生的新树有dp[j]*dp[n-j-1]个
42.(662:Medium)(非常经典题)Maximum Width of Binary Tree
- 要解决该题,其实要把这个非完全二叉树看作完全二叉树,然后用完全二叉树的性质进行求解:对于位置i,它的左孩子是2*i,右孩子是2*i+1。
- 因为一个完全二叉树可以用数组按上面的性质来存储,所以我们直接用一个队列存储实际存在结点的位置下标。之前尝试每层都建立一个长度为2*i的数组来标记每个位置是否有结点还是null结点,但当层数很深时,会内存溢出,所以这里改用只存储非空节点位置下标的方法避免该问题。因此我们用两个队列q和pos, p专门存储非空结点,pos用来存储非空结点在数组中的位置,这两个队列中的元素是相等的且是一一对应的,然后按BFS的思路进行求解即可,每次遍历某一层的时候,用两个变量start和end来标记第一个结点和最后一个结点在完全二叉树数组中的位置,搜索完一层后,比较一下宽度即可。
- 上面的思路beat 60%+,具体实现细节参看代码实现(代码注释有一些注意点)。
discuss中貌似还有其他DFS的方法,下次复习时再学习
43.(129:Medium)Sum Root to Leaf Numbers
- 该题就是一个简单的DFS应用,我们在每次进行dfs的时候,再多传入一个参数是从根到当前结点的数值,即1->2->3,在结点2时,该值为12,那么在往下层搜索时,它的值为12*10+3=123。此外我们再维护一个成员变量sum,当搜索到叶子结点时,将当前叶子结点的值加到sum上即可。
44.(450:Medium)(经典题)Delete Node in a BST
- 该题其实是一个删去二分搜索树中间结点后重构的问题,因为删去中间结点后涉及到树结构的重建,所以需要分几种情况讨论。示例图如下:
假设被删节点的key=4
第一种情况:被删结点的左右子树至少有一个为null
10 10
/ /
4 => 1
/
1
第二种情况:被删结点左右子树均不为null,且被删结点的右子树根结点的左子树为null
10 10
/ /
4 => 7
/ \ / \
1 7 1 8
\
8
第三种情况:被删结点左右子树均不为null,且被删结点的右子树根结点的左子树不为null
10 10
/ /
4 => 7
/ \ / \
1 7 6 8
/ \ /
6 8 5
/ /
5 1
45.(103:Medium)Binary Tree Zigzag Level Order Traversal
- 该题很简单,就是一个BFS的应用,类似于第39题(102),在第39题的基础上,只需要维护一个dir方向变量,当dir=1时正序搜索,当dir=-1时倒序搜索。
46.(652:Medium)(非常经典题)Find Duplicate Subtrees
- 该题一开始想每次比较子树时都重复递归DFS一遍,当树的结构是单分支的一条线时,非常耗费时间。且无法分辨该相同的子树之前是否已经被记录到结果集中,得重新dfs判断,超时。
- 正确的思路是:将树的结构以字符串形式(先序遍历)进行存储,从而避免了多余的重复的递归操作,节省了时间,对于null结点,我们也需要以“#”进行记录,这样才能存储树的结构。同时以map集合记录子树出现的频率,避免了相同子树在结果集中重复记录的可能性,key是子树的先序遍历字符串,vlaue是该子树出现的频率。只有当我们在比较前,该子树出现的频率为一次时,才将该相同子树加入到结果集中,否则说明之前已经加入过了。
47.(114:Medium)(非常经典题)Flatten Binary Tree to Linked List
- 该题其实就是一个递归调整树结构的问题,我们从最底层来观察,当一个最底层的子树根节点左右各有一个叶子结点时,我们只需要将该根节点的左子树置为null,而原来的左子树变为该根节点的右子树,原来的右子树作为新的右子树最右下叶子结点的右子树。按这样的建树规则,我们将其应用到整个树与其左右子树上,递归方法求解即可。具体的实现细节思路参看代码。
48.(116:Medium)Populating Next Right Pointers in Each Node
- 该题就是BFS的典型应用,我们在从队列中取每层结点的时候,都维护一个pre指针指向当前结点node的前一个结点,然后使pre.next = node,直到BFS搜索完毕。
该题在discuss中还有其他更高效的答案,不需要使用BFS及队列,只需要用递归,下次复习时再研究
<49>?.(113:Medium)(经典题)(有疑问)Path Sum II
- 该题其实和第19题(112)一样,只不过多了一个路径的存储。
疑问:在传List引用的时候传的应该是指针地址,所以避免list集合的共享应该新建list将其中元素拷贝后再往下层传。但discuss中答案却直接传的地址而且还被accept,不懂为什么,下次复习时与其他同学讨论
50.(117:Medium)Populating Next Right Pointers in Each Node II
- 该题好像去掉了“完全二叉树”的限制,成为了一个普通的二叉树。使用与第48题(116)相同的代码(BFS思路)也能通过OJ被accept。
<51>.(95:Medium)(非常非常经典题)Unique Binary Search Trees II
- 该题沿用第41题(96)的DP动态规划思路,但因为该题目让返回树,所以我们应该对遍历过得结点树进行存储。该题的难点在于:获得了新的根节点的左右子树,如何建立新的二叉搜索树。
- 一开始我尝试在建立好正确结构的二叉树基础上,通过调整每个结点的值来将其变为二叉搜索树,但并没有实现成功。Disucuss中DP方法的巧妙方法是根据之前的树集合构造新树,且通过偏移量将其调整为了二叉搜索树。我们在遍历到n个结点时,前面存储着1...n-1对应的所有二叉树,但可惜的是他们的结点值都是从1开始的,所以我们通过将右子树增加一个偏移量,建立符合条件的二叉搜索树。该题具体的实现思路细节参看代码实现和相关注释。
该题除了DP思路以外,discuss中还有直接建树的方法,下次复习时应研究学习
52.(236:Medium)(非常经典题)Lowest Common Ancestor of a Binary Tree
- 该题是第21题(235)的扩展,一开始尝试使用第21题(235)第二种更一般的解法,但发现该题的树节点val值可以重复,所以需要单独处理左右子树中p、q结点的个数。但是经过代码的修改,一直不能通过第30/31个test case。
- discuss中有高票答案,非常巧妙。当遍历到的某一个结点值非null且等于p或q时,直接返回该结点给上层,此时包含两种情况:一种是root及其子树上只有一个p或q结点,此时当然是返回root;第二种情况是,root及其子树上包含有p和q结点,此时root就是最小的祖先,应返回root。如果当前的结点不为null,但也不等于p和q,则继续递归搜索左右子树,当左右子树递归函数返回值只有一个非空结点,则将其返回给上层;若均不为null,则当前层遍历的结点就是最小祖先,将其返回;否则返回null。该代码如下:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//当root不为null时,包含两种情况:一种是root及其子树上只有一个p“或”q结点,此时当然是返回root;第二种情况是,root及其子树上
//包含有p“和”q结点,此时root就是最小的祖先,应返回root
if (root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left!=null && right!=null)
return root;
if(left!=null && right==null) //如果直到根节点那层都只有一侧子树返回有具体结点,而另一侧返回null,说明p、q均在那个返回为非空结点的子树上
return left;
if(left==null && right!=null)
return right;
//左右结点均为null
return null;
}
53.(222:Medium)(非常经典题)(有疑问)Count Complete Tree Nodes
- 该题使用BFS或者DFS求解均超时,只不过DFS的效率要比BFS高而已。正确的方法当然还是利用完全二叉树的性质。
- 因为该题并没有将结点存入数组中,所以不能使用左右孩子结点的位置是根节点的二倍或者二倍加一的性质。而应该利用完全二叉树的高度特性,比较以某一个结点为根的左右子树高度,从而求得树的结点数量。代码见下:
public int countNodes(TreeNode root) {
int leftDepth = leftDepth(root);
int rightDepth = rightDepth(root);
if (leftDepth == rightDepth) //说明叶子结点布满了最后一层,对这样的满二叉树,结点总数为2^h-1,h为树高
return (int)Math.pow(2, leftDepth) - 1;
//return (1 << leftDepth) - 1;
else//说明以当前结点为根的子树上,最后一层并不是2^(h-1),即该子树不是满二叉树,所以递归求其左右子树的节点数,看看是否为满二叉树,1代表当前的根节点
return 1+countNodes(root.left) + countNodes(root.right);
}
private int rightDepth(TreeNode root) {
// TODO Auto-generated method stub
int dep = 0;
while (root != null) {
root = root.right;
dep++;
}
return dep;
}
private int leftDepth(TreeNode root) {
// TODO Auto-generated method stub
int dep = 0;
while (root != null) {
root = root.left;
dep++;
}
return dep;
}
该题中,在求满二叉树的结点个数时,discuss中是按位移操作计算的,(1 << Depth) - 1。但自己并不懂这是什么意思,且该计算方法应该要比调用Math包的pow函数效率高的多。下次复习时再和别的同学请教。
54.(98:Medium)(经典题)Validate Binary Search Tree
- 该题其实难度并不大,但需要注意几点:1. 对于右子树,右子树上的所有结点值都要比根节点值大,左子树上的所有结点值都要比根节点值小,因此我们在向下层递归搜索时,需要向函数传入一个上限值、一个下限值。 2. 最后几个test case中,结点值全部都是int的最大值2147483647或最小值-2147483648,所以我们应该将上限值和下限值参数的类型调整为long型。
55.(145:Hard)(非常经典题)Binary Tree Postorder Traversal
- 该题的递归DFS方法很简单,也很高效,beat 98%。
- 对于该题的迭代循环解法,相比于之前的前序和中序遍历而言可能稍复杂。但我们仍可以将其转化为先序遍历,假如每次我们都将当前结点插入结果集的最开始位置,则有:根节点->右子树、根节点->左子树、右子树、根节点,巧妙地将其转化为另一种版本的中序遍历。具体可以参考代码实现。
参考链接:前序、中序、后序遍历迭代写法,只有一层while循环,强烈建议看
下次复习时应参看上面的参考链接,其中的迭代循环解法只涉及到一层while循环,面试时更容易想到且易理解
56.(297:Hard)(非常非常经典题)Serialize and Deserialize Binary Tree
- 该题类似于第38题(449),只不过第38题需要序列化的是一个二分查找树,而此题只是一个普通的二叉树。
- 正如在第38题中的分析,对于普通的二叉树,我们必须用一个字符来代表null结点。在Discuss中,高票答案思路是:用先序遍历来存储树的搜索结果,null结点用"X"表示,每个结点值用","分隔以便反序列化时读取。在反序列化时,我们用一个队列从队头开始依次取出结点,而每次取出的结点都是该子树的树根,同时也是之前结点的子树,于是便可按该思想建树。具体的实现细节参看代码实现。
57.(99:Hard)(非常非常经典题)Recover Binary Search Tree
- 在做题之前,我们需要先明确一点:中序遍历"二分搜索树",出现的节点的值会升序排序,如果有两个节点位置错了,那肯定会出现降序。因此,我们设置一个pre节点指针,记录当前节点中序遍历时的前节点,如果当前节点小于pre节点的值,即pre.val >= cur.val,说明需要调整次序。具体来讲,如果在中序遍历时节点值出现了两次降序,第一个错误的节点为第一次降序时较大的节点,第二个错误节点为第二次降序时较小的节点。比如,原来的二叉搜索树在中序遍历的节点值依次为{1,2,3,4,5},如果因为两个节点位置错了而出现{1,5,3,4,2},第一次降序为5->3,所以第一个错误节点为5,第二次降序为4->2,所以第二个错误节点为2,将5和2换过来就可以恢复。
上面的方法空间复杂度为O(1),之存储了pre变量和两个需要交换的元素变量。题目中提示有O(n)的解法,下次复习时再研究学习
58.(834:Hard)(未做)Sum of Distances in Tree
- 该题因为题号太后并没有做,但点赞数达到了88:3,应该是一道好题,下次复习时再研究该题。
- 这里给出该题出题人的参考答案与分析链接:参考答案与分析
<59>.(685:Hard)(非常非常经典题)Redundant Connection II
- 该题是第36题(684)的扩展,但它从无向图变成了有向图,所以父亲-孩子关系变得非常清晰。因此,在判断环的基础上,我们还需要判断每个结点的父节点是否只有一个,这样可以分为以下三种情况:
- 有向图中只有环,而每个结点的父节点不多于1个,则删除最后一个造成环的边即可
- 有向图中没有环,存在一个结点有两个父亲,则删除后一个造成该结点有多个父亲的边即可
- 有向图中既有环,也有一个结点有两个父亲,我们应该
删除其中一个与父亲相连的边,同时该边也必须在环中
如下图所示:
- 在上面分析的基础上,我们应该执行两次for循环操作。第一次循环查找是否有结点存在多个父亲,若存在则记录与父亲相连的两条边,以判断其中哪一条在环中,若没有环则返回第二条边即可。第二次循环同第36题(684)无向图原理一样,将该有向图看作无向图,查找每个结点的root根,即连通分量的代表结点,根据union-find操作判断是否有环,然后根据上面的三种情况作判断来返回结果。
- 在实际编码过程中,运用了一些小的技巧,例如在edges数组中将有多个父亲的结点的第二条边在edges数组中赋值为{0,0},方便后边查环操作的实现。
- 上面的文字表述可能不严谨,也不是很清晰,具体的实现思路请直接参看实现代码和注释,非常条理。
参考链接:Redundant connection I/II详解含代码
60.(124:Hard)(非常非常经典题)(有疑问,已解答)Binary Tree Maximum Path Sum
- 该题其实和前面某道题相似,不仅需要比较单边支路的和,也需要以某一个结点为中心的折线段的和,区别在于:该题的path路径终点不一定是叶子结点,而起始结点和前面那道题一样,不一定是树的根节点。
- 该题同样也是用递归做,然后在每层递归的时候,比较单边支路和、折现段和,并且将较大单边支路返回给上层。
如果该题中结点值均小于0,已提交的accept代码是不是会有问题?下次复习时再仔细研究
回答上面的疑问,答案是否定的,已提交代码没问题,因为每层向上一层返回时,返回的值是return Math.max(left, right) + node.val,即返回的至少是根节点大小的值,当左右路径和均小于0时,前面的代码已将left和right置为0,所以当整棵树的结点值均小于0时,程序结果应为root.val即树根的值
61.(865:Medium)(经典题)Smallest Subtree with all the Deepest Nodes
- Write a sub function
deep(TreeNode root). It returns apair(int depth, TreeNode subtreeWithAllDeepest)
In sub function deep(TreeNode root):
if root == null, return pair(0, null)
left = deep(root.left)
right = deep(root.left)
if left depth == right depth,
there are deepest nodes both in the left and right subtree,
return pair (left.depth + 1, root)
if left depth > right depth,
there are deepest nodes only in the left subtree,
return pair (right.depth + 1, left subtree)
if left depth < right depth,
there are deepest nodes only in the right subtree,
return pair (right.depth + 1, right subtree)
62.(285:Medium)(非常经典题)Inorder Successor in BST
- 宗旨:可以这样理解,中序遍历,p的后继值一定都比p大,那么当root值已经大于p,就要缩小root值,找最接近p的node,所以root要遍历左子树;当root的值比p的值小,此时root不可能是p的后继,此时应该增大root的值直到恰好大于p。代码如下:
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
TreeNode succ = null;
while (root != null) {
//可以这样理解,中序遍历,p的后继值一定都比p大,那么当root值已经大于p,就要缩小root值,找最接近p的node,所以root要遍历左子树;当root的值比p的值小,此时root不可能是p的后继,此时应该增大root的值直到恰好大于p
if (p.val < root.val) { //当p在root的左子树上时,才记录succ,因为当前的root可能就是p的successor
succ = root;
root = root.left;
}
else
root = root.right; //如果p在root的右子树上时,我们不记录succ,因为肯定存在比p还大的元素,或者是null
}
return succ;
}
63.(428:Medium)(非常经典题)Serialize and Deserialize N-ary Tree
- Idea: preorder recursive traversal; add number of children after root val, in order to know when to terminate.
- Example: The example in description is serialized as: "1,3,3,2,5,0,6,0,2,0,4,0"
- 所以在每次序列化的时候都把结点值和当前结点的孩子数量存入list中,然后递归序列。同样在反序列化的时候,先把结点值和孩子个数读出来,然后递归的建树。参考代码如下:
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val,List<Node> _children) {
val = _val;
children = _children;
}
};
// Encodes a tree to a single string.
public String serialize(Node root) {
List<String> list=new LinkedList<>();
serializeHelper(root,list);
return String.join(",",list);
}
private void serializeHelper(Node root, List<String> list){
if(root==null){
return;
}else{
list.add(String.valueOf(root.val));
list.add(String.valueOf(root.children.size()));
for(Node child:root.children){
serializeHelper(child,list);
}
}
}
// Decodes your encoded data to tree.
public Node deserialize(String data) {
if(data.isEmpty())
return null;
String[] ss=data.split(",");
Queue<String> q=new LinkedList<>(Arrays.asList(ss));
return deserializeHelper(q);
}
private Node deserializeHelper(Queue<String> q){
Node root=new Node();
root.val=Integer.parseInt(q.poll());
int size=Integer.parseInt(q.poll());
root.children=new ArrayList<Node>(size);
for(int i=0;i<size;i++){
root.children.add(deserializeHelper(q));
}
return root;
}
64.(783:Easy)(经典题)Minimum Distance Between BST Nodes
- 该题一开始认为最小差值只存在于相邻的父子结点之间,但发现test case通不过,例如下例,最下差值为1(90-89)。所以为了解决该问题,应使用中序遍历,保证搜索的值是从小到大排列的,用pre指针记录前一个结点,从而获取在中序遍历过程中,相邻两个访问节点的差值。
90
/ \
60 200
/ \
50 89
65.(701:Medium)Insert into a Binary Search Tree
- 如果插入的val值比当前结点值大,则向右搜索,否则向左搜索。按此思路直到到达一个null结点,然后插入即可。
66.(863:Medium)(非常非常经典题)All Nodes Distance K in Binary Tree
- 该题可以将树建成一个无向图,然后从target出发,BFS寻找走K步能到达的所有结点。具体请参考代码。
- 上面的思路比较好理解,但时间复杂度相对高一些,还有使用Recursive的方法,具体可以参考下面的花花讲解链接。
- 参考链接:花花讲解:Graph+BFS and Recrusive
67.(958:Medium)(非常非常经典题)Check Completeness of a Binary Tree
- 核心思想:在BFS过程中,null结点后不应再出现任何有效结点,否则不complete。When level-order traversal in a complete tree, after the last node, all nodes in the queue should be null. Otherwise, the tree is not complete.
public boolean isCompleteTree(TreeNode root) {
boolean end = false;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll(); //如果tree是complete的,那么可能只有队列的最后连续几个元素是null的,因为倒数第二层的后面几个树结点可能没有左右孩子,此时会append进null空结点
if(cur == null) end = true; //对于null结点,我们不访问它的左右子树
else{
if(end) return false; //当null元素后仍然存在有效结点时,说明tree是不完整的
queue.add(cur.left);
queue.add(cur.right);
}
}
return true;
}
68.(897:Easy)(非常经典题)Increasing Order Search Tree
- 参照如下的DFS思路,始终记录前一个结点,从而便于拼接
TreeNode prev=null, head=null;
public TreeNode increasingBST(TreeNode root) {
if(root==null) return null;
increasingBST(root.left);
if(prev!=null) {
root.left=null; // we no longer needs the left side of the node, so set it to null
prev.right=root;
}
if(head==null) head=root; // record the most left node as it will be our root
prev=root; //keep track of the prev node
increasingBST(root.right);
return head;
}
69.(872:Easy)(非常经典题)Leaf-Similar Trees
- 直白的思路是,先遍历第一个树,将其叶子按序保存在list中,然后遍历第二个树,按序与第一个树list的对应位置进行比较。优化:用字符串拼接所有叶子结点,最后通过字符串比较判断两个树的叶子是否相同。具体思路可以参看代码。
70.(1008:Medium)(经典题)Construct Binary Search Tree from Preorder Traversal
- 该题只要顺次从list中取元素当作树节点即可,通过当前value值和之前的value值额外判断是左子树还是右子树。代码如下:
int i = 0;
public TreeNode bstFromPreorder(int[] A) {
return bstFromPreorder(A, Integer.MAX_VALUE);
}
public TreeNode bstFromPreorder(int[] A, int bound) {
if (i == A.length || A[i] > bound) return null;
TreeNode root = new TreeNode(A[i++]);
root.left = bstFromPreorder(A, root.val);
root.right = bstFromPreorder(A, bound);
return root;
}
71.(1008:Medium)(非常非常经典题)Construct Binary Search Tree from Preorder Traversal
- For each node, we use an int array to record the information
[# of nodes in the subtree (include itself), # of total coins in the subtree (include itself)]. Then we know that for a certain node, if there aremore coins than nodesin the subtree, the node must "contribute" the redundant coins to its parent. Else, if there aremore nodes than coinsin the subtree, then the node must take some coins from the parent. - Both of these two operations will create moves in the tree. And we just need to add the
absolute valueof the (# nodes - # coins) to the final result because the move can be "contribute" or "take". The time complexity is O(n) because we are just traversing the tree.
72.(1026:Medium)(非常经典题)Maximum Difference Between Node and Ancestor
- We pass the minimum and maximum values to the children. At the leaf node, we return
max - minthrough the path from the root to the leaf. - 自上而下把路径上的最大最小值传下去即可,在子树的末端即叶子结点处进行最大最小值差值的比较
73.(938:Easy)(经典题)Range Sum of BST
- 可以利用BST的性质来进行剪枝,只将在[L,R]范围内的值进行求和。
74.(965:Easy)Univalued Binary Tree
- 只要子树非空,就比较子树上的值与根节点的值是否相等
75.(894:Medium)(非常非常经典题)All Possible Full Binary Trees
- For all combinations of left and right number of children: 1. Recurse into left and right subtree; 2. Combine results
- Note that there is no valid answer for even number of nodes, so we may add an early exit there.
- 核心思路是,我们用recursive的方法,用给定的剩余节点数构建所有可能的满二叉树,并返回给上层用于拼接。
public List<TreeNode> allPossibleFBT(int N) {
List<TreeNode> list = new ArrayList<>(); //用当前层的剩余结点个数N构建的所有可能的满二叉树
if (N % 2 == 0) return list; //当N为偶数时,肯定不可能构建成满二叉树
if (N == 1) {
list.add(new TreeNode(0));
return list;
}
//下面的变量leftNum是用来构建满二叉左子树的,N-leftNum-1用来构建满二叉右子树,1代表当前层的根节点
for (int leftNum = 1; leftNum <= N-1; leftNum += 2) { // 因为只有奇数才能构建满二叉树,所以一次增加2,至于右子树的结点个数,当偶数时由程序开始的if条件来handle
List<TreeNode> fLeft = allPossibleFBT(leftNum);
List<TreeNode> fRight = allPossibleFBT(N-leftNum-1);
for (TreeNode left: fLeft) {
for (TreeNode right: fRight) {
TreeNode node = new TreeNode(0); //拼接所有可能的满二叉左右子树
node.left = left;
node.right = right;
list.add(node);
}
}
}
return list; //将总结点个数为N的当前层的所有可能的满二叉子树返回给上层
}
76.(951:Medium)(非常非常经典题)Flip Equivalent Binary Trees
- 按题目条件,若两个数时flip equivalent的,需要满足:当前比较的两结点必须同时为空,或者均不为空且值相等,此外,他们的子树配对原则有两种:不是左子树和左子树,右子树和右子树配对;就是左子树和右子树,右子树和左子树配对,没有其他情况。
public boolean flipEquiv(TreeNode r1, TreeNode r2) {
// 有一个为空就返回false,因为二者必须一致
if (r1 == null || r2 == null) return r1 == r2;
//均非空时,值必须相等
if (r1.val != r2.val) return false;
//注意:不是左子树和左子树,右子树和右子树配对;就是左子树和右子树,右子树和左子树配对。没有其他情况
return flipEquiv(r1.left, r2.left) && flipEquiv(r1.right, r2.right) || flipEquiv(r1.left, r2.right) && flipEquiv(r1.right, r2.left);
}
77.(979:Medium)(非常非常经典题)Distribute Coins in Binary Tree
- 该题计算子树具有的总coin数量和该子树的总结点数量,当二者相等时,说明该子树内部可以自己调节使每个结点上至少有一个coin,否则的话需要该子树的结点给该子树进行coins的输送,而一次move只能移动一个coin。具体的代码如下:
int moves = 0;
public int distributeCoins(TreeNode root) {
getNumAndCoins(root);
return moves;
}
/*
* return [number_of_nodes_in_subtree, number_of_total_coins_in_subtree]
*/
private int[] getNumAndCoins(TreeNode node) {
if (node == null) return new int[] {0, 0};
int[] left = getNumAndCoins(node.left);
int[] right = getNumAndCoins(node.right);
moves += Math.abs(left[0] - left[1]) + Math.abs(right[0] - right[1]); //判断当前的根节点是否需要给左右子树输送coins,如果左右子树的coins总数和节点数的差为0,说明他们可以自己调节,需要移动的次数在下层递归时就已经考虑过了
return new int[] {left[0] + right[0] + 1, left[1] + right[1] + node.val};
}
78.(1110:Medium)(非常非常经典题)Delete Nodes And Return Forest
- 该题将array转化成一个set,然后遍历每个根节点判断当前结点是否是待删除结点,这种思路要比你对每一个指定的待删除结点去整个树里面搜索处理起来容易的多。参考代码如下:
//注意:这不是一个BST,所以我们不知道给定的to delete value在哪个子树上
Set<Integer> to_delete_set;
List<TreeNode> res = new ArrayList<>();
public List<TreeNode> delNodes(TreeNode root, int[] to_delete) {
res = new ArrayList<>();
to_delete_set = new HashSet<>();
for (int i : to_delete) //将数组存成set,然后对每个结点都进行是否delete的判断要比指定一个删除的值在树里找简单
to_delete_set.add(i);
helper(root, true);
return res;
}
private TreeNode helper(TreeNode node, boolean is_root) {
if (node == null) return null;
boolean deleted = to_delete_set.contains(node.val);
if (is_root && !deleted) res.add(node);
node.left = helper(node.left, deleted);
node.right = helper(node.right, deleted);
return deleted ? null : node;
}
79.(1145:Medium)(非常非常经典题)Binary Tree Coloring Game
- 因为为了使second player赢,我们应将他的node放置在紧挨first player的位置上,这样才能尽量占据更多的node。那么在树上,可以以first player的第一个结点作为分界线,将整个树分成三个部分,first layer node以上的部分以及他的左右子树,当这三个部分有一个集合的size大于总共node的一半,second player就一定能赢。
- Follow up:如果作为first player选一个node一定能赢,这个node应该选择在使整个树节点二分的位置上,这样肯定就能赢,即三个集合中最大的集合应等于另外两个集合size的和。
80.(1038:Medium)(非常非常经典题)Binary Search Tree to Greater Sum Tree
- 我们只需要按中序遍历的逆序,先办理右子树->根->左子树,这样在遍历到根的时候,就知道比当前结点值大的所有结点之和是多少了
int pre = 0;
public TreeNode bstToGst(TreeNode root) {
if (root.right != null) bstToGst(root.right);
pre = root.val = pre + root.val;
if (root.left != null) bstToGst(root.left);
return root;
}
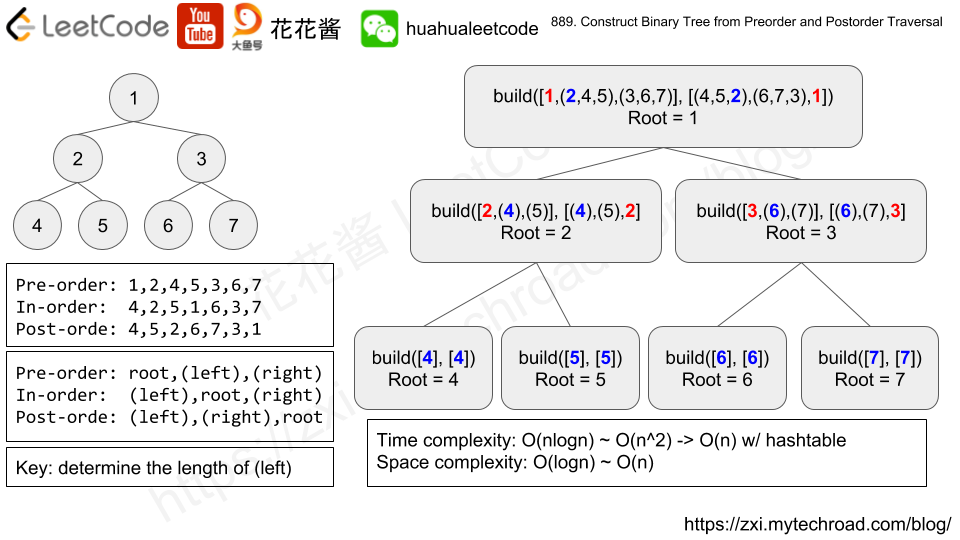
81.(889:Medium)(非常经典题)Construct Binary Tree from Preorder and Postorder Traversal
- 关键:找到当前结点左子树根节点在后续遍历过程的左边界,从而算出左子树遍历序列的长度
//优化:因为build函数需要在post序列中找某个结点的索引,所以可以用一个hashmap预处理,将post traversal中各个结点的值及索引存到map中
public TreeNode constructFromPrePost(int[] pre, int[] post) {
return build(pre, post, 0, 0, pre.length);
}
//segmentLen代表当前遍历子树的序列长度
public TreeNode build(int[] pre, int[] post, int preIndex, int postIndex, int segmentLen) {
if(segmentLen <= 0) return null;
TreeNode root = new TreeNode(pre[preIndex]);
if(segmentLen == 1) return root;
int k = postIndex;
// root,left,right; left,right,root; 该循环是为了找到当前结点左子树根节点在后续遍历过程的左边界,从而算出左子树遍历序列的长度
while(post[k] != pre[preIndex+1]) k++;
int newSegmentLen = k - postIndex + 1; //当前根节点左子树遍历的序列长度
root.left = build(pre, post, preIndex+1, postIndex, newSegmentLen);
root.right = build(pre, post, preIndex+newSegmentLen+1, k+1, segmentLen-newSegmentLen-1); // 1代表当前层root
return root;
}
- 参考链接:花花视频讲解