String (Java) - ShuweiLeung/Thinking GitHub Wiki

1.（657:Easy）Judge Route Circle

• 该题是第一道使用Java来实现的题目，发现对Java的使用目前很生疏，需要勤加练习。
• 第一次看到该题时，发现题目与“括号匹配问题非常相似”，区别在于括号匹配中，“{[}]”的字符不符合要求，但本题里“RLRL”却是符合题意的解，因此，我们不需要使用“堆栈”数据结构，只需要遍历一次字符串，统计R、L、U、D的字符数量，最后比较R=L，U=D是否相等即可。
• 注意：字符串可以使用toCharArray()方法转化为字符数组，从而使用增强for进行遍历。

2.（344:Easy）Reverse String

• 该题非常简单，只需要实现将字符串倒序的操作。我们可以设置两个指针，分别从首尾两侧向中间遍历，交换两指针当前位置的元素直到相遇，但因为Java中字符串的内容是不可改变的，所以，我们只能新开辟一个空间返回新的字符串。因为我们在操作过程中字符是可变的，故这里选择StringBuffer容器类，设立一个指针从末尾扫描到开头来进行字符串的反转。
• 也可以将字符串转化为字符数组进行处理，这样通过下标访问元素处理更高效，最后只需要将字符数组再转化回字符串即可（String.valueOf()或new String()）。

3.（541:Easy）Reverse String II

• 该题一种思路是，我们逻辑上以2k长度将String字符串分段，对每段进行前k个字符串的倒序操作，对String字符串末尾可能不满足2k长度的部分，我们需要特殊处理，判断剩余长度是否大于k，并据此进行最后的特殊处理。该题还是可以将字符串转化为一个字符数组进行处理。

4.（557:Easy）Reverse Words in a String III

• 我的思路为，利用String的split方法分割为字符串数组，然后按照第2题（344）的思路，用一个StringBuffer容器类来保存最终的结果，将每个单独的字符串处理完后拼接到StringBuffer中同时加上空格，最后将其返回即可。

只beat 35.6%，可能有更好的方法，下次复习时再研究

5.（521:Easy）（理解本质）Longest Uncommon Subsequence I

• 个人认为该题的题目表达不清楚，解题思路很简单，但题目表述很复杂。当输入的字符串a、b完全相等时，返回-1；否则，返回a、b中较大的字符串长度。关键是，subsequence可以是字符串本身，当两字符串不同时，那么其中较长字符串本身一定不会是另外一个字符串的子串。

6.（520:Easy）Detect Capital

• 该题只需要依照返回true的三个条件依次判断即可，建立全大写字符串，零大写字符串和首字母大写字符串，分别进行比较。char小写字符通过转换成int型然后-32可将大写转换成小写，同理大写字符转化成int型+32可抓换为大写。
• 另一种方法不需要分配额外空间，直接通过遍历每个字母的值是在'a'-'z'还是‘A’-'Z'之间（word.charAt(i)>='a'&&word.charAt(i)<='z'），统计大写字母个数来进行判断。

7.（788:Easy）Rotated Digits

• 该题有两种方法：一种是将整数转化为字符串，然后判断该字符串是否含有“符合条件”或“不符合条件”的数字字符；第二种，是利用取余运算，获得个位数后进行判断，然后将原整数进行地板除法除以10，继续循环进行上述运算直到原整数变为0。

8.（696:Easy）（经典题）Count Binary Substrings

• 该题难度有些上升，我们可以设立两个指针i、j，i指针永远指向grouped subsequence的第一个字符位置，而j指针一直后移统计0、1字符的个数，直到当前j指针所指字符s[j]!=s[j-1]同时s[j]=s[i]，说明我们已经找到了当前长度最大的grouped subsequence，i指针是该序列的起始位置，j指针是终止位置+1，那么该序列的符合条件的子字符串个数是min(0字符数量，1字符数量)。至此为止，以s[i]开头、s[j]结尾的子序列已统计完毕，那么接下来我们应该移动i指针的位置到合适位置，如下图例所示:

  “0011001”   第一个箭头所指的是当前i指针的位置，第二个箭头是当前j指针的位置，
   ^   ^      我们现已将i、j所夹序列统计完毕。

  “0011001”   接下来我们只需要移动i指针到上一个序列中第一个‘1’字符所在位置，开启新的循环即可
     ^ ^      此时1字符数量为2，0字符数量重置为0

• 即，当j指针指的是'0'字符时，i指针应重置为“i = j - numOf1”；若j指针指的是'1'字符时，i指针应重置为“i = j - numOf0”，然后继续按上面的思路循环直到j=s.length()。

上面的思路只beat 9%，应有更快的方法，还未参考discuss，当下次看到这句话的时候再看，复习时也需要看

9.（606:Easy）Construct String from Binary Tree

• 该题只是一个最简单的先根遍历的题目，题目本身没有什么难度，关键在于在返回序列中需要用括号来区分左右子树，所以我们在每一层的遍历中，用一个临时的变量temp存储以当前结点为根的左右子树遍历结果，然后与上层传来的preorder序列以**"("+temp+")"**的形式进行拼接，从而为遍历结果加上括号。
• StringBuilder有与StringBuffer兼容的API，但不保证同步。该类被设计用作 StringBuffer 的一个简易替换，用在字符串缓冲区被单个线程使用的时候（这种情况很普遍）。如果可能，建议优先采用该类，因为在大多数实现中，它比StringBuffer要快。

10.（13:Easy）Roman to Integer

• 该题首先需要明白罗马数字的计算规则是什么？罗马数字就有下面七个基本符号：I（1）、V（5）、X（10）、L（50）、C（100）、D（500）、 M（1000）。用罗马数字表示数时、如果几个相同的数字并列、就表示这个数的值是数码的几倍。例如：罗马数字要表示 3、可以写成 Ⅲ；要表示 20，可以写成 XX；要表示 30、可写成 XXX。不相同的几个数码并列时，如果小的数码在右边，就表示数的数值是这几个数码的和；如果小的数码在左边，就表示数的数值是数码之差。
• 根据上面的计算规则，我们可以依次读取输入的罗马数字字符串，如果当前的罗马数字字符比下一个罗马数字字符小，则在原有数字的基础上减去当前数字，否则加上当前数字。为了处理方便，照顾到输入字符串的最后一个字符，我们在输入字符串末尾添加一个‘I’字符，因为原字符串最后一个字符代表的数字肯定是要加的，而不是减去。

11.（383:Easy）（经典题）Ransom Note

• 问题所涉及到的数据结构其实并不复杂，没有必要用各种容器类或数组间的相互转化。一种方法是使用Map，建立一个ascII表（或建立一个26个字母的表，用“c-'a'”定位），用一个int型的数组来实现，长度为128，初始化为0，开始遍历字符串magazine在ascII表中将字符的数量统计出来，然后遍历ransomNote字符串，若该字符在当前ASCII表中的数量大于0，则将对应数量-1，否则返回false。
• Map容器类的getOrDefault(c,0)函数，若字符存在则返回对应值，否则返回0。

12.（387:Easy）（经典题，看注意事项）First Unique Character in a String

• 该题有两种思路，第一种方法比较笨：用一个容器类Map存储扫描过程中的信息，key是字母字符，value是一个ArrayList，其中第一个位置存储着对应字母的出现次数，第二个位置存储着该字母首次出现的位置。我们遍历一次输入的String字符串后，再遍历Map的value值，取其中只出现一次，且出现位置最小的值并将其位置返回。
• 第二种方法很高效：思路同第一种类似，只不过该方法并不使用Map和ArrayList，我们只是在第一次遍历字符串的时候用一个长度为26的整型数组存储每个字母的频率。第二次同样也是遍历字符串，只不过我们在遍历过程中通过**c-'a'(c为当前字符变量)**获取当前字符的频率，若为1则直接返回此刻的数组下标，否则继续扫描。因为第二次遍历时，指针是从前往后扫描的，所以当遇到某个字符在整个字符串中只出现了一次时，该字符一定是“最先出现的”且“只出现过唯一一次的”字符。
• 注意：1、只有在main函数或者大括号内才能声明变量，否则报错。如下所示：

  if(a == b)
      //Java中不加大括号不能声明变量,这样是错误的，IDE报错
      int c = 3; 
  if(a == b){
      int c = 3;     //加上大括号后才正确
  }

• 2、容器类的读取效率远远低于数组的读取，且对于字符串类的问题，我们可以建立长度为26的数组起到一个字典(Map)的功能。
• 3、Java是强类型语言，如我们通过ArrayList对象list取其中的第一个元素，list.get(0)，即使我们知道该值是int(Integer)类型，但我们通过get操作取出的却是一个Object类型，不能直接进行运算，此时我们需要进行强制类型转换(int)list.get(0)，来实现数学运算操作。

13.（551:Easy）Student Attendance Record I

• 该题较简单，只需要在遍历输入字符串的同时统计A、L的个数，注意：三个连续的L才会返回false，所以当当前的字符不是‘L’时，需要将‘L’字符的个数清零。

14.（345:Easy）Reverse Vowels of a String

• 该题较简单，只需要设立两个指针i、j分别指向字符串的首尾位置，i从前向后扫描直到遇见元音停止，类似地，j从后往前扫描直到遇见元音停止，然后交换i、j位置上的字符，交换结束后i、j分别+1和-1，继续上述的循环直到相遇。
• 注意：大写元音、小写元音都应该被交换。

15.（459:Easy）（稍有难度）Repeated Substring Pattern

• 一开始拿到该题时，想找到最小的可重复子字符串，但发现非常困难，如：“ababc”，当扫描完第二个“ab”时，我们可能会做出最短的可重复子字符串是“ab”的判断，但显然该判断是错误的。同样，如“ababcababcababcabcd”，可能我们会认为最短的重复子字符串是“ababc”，但实际上也是错误的。因此，我们从上面的例子可以发现，直接找出符合条件的子字符串是困难的，比较难判断，所以应该换一个角度来解答该问题。
• 一种思路是，我们认为存在某个可重复的子字符串，并且该字符串重复n次即得当前的输入字符串，我们从n=2开始进行尝试，n的上限是输入字符串的长度。也就是说，我们从“将整个输入字符串分成两半”开始，一直循环判断相邻的两个子字符串（不一定是最短的）是否是相等的，若相等则判断接下来两个相邻的子字符串直到所有的子字符串都被判定为“相等”，说明该字符串符合条件返回true；否则，若某两个相邻的子字符串不相等，则应该增加分段的个数（如将字符串从原来的分成两段增长为分成如今的三段、四段...）。分段个数的上限是输入字符的长度，相当于每一个子字符串都是单独的一个字符，若还不两两相等，则说明输入的字符串不符合条件，返回false即可。对于如何确定分段的个数fold，假设输入字符串长度strLen，则应满足strLen%fold=0。（beat 71%）
• 用dicuss中的思路来简要表达上面的思想：

  1.The length of the repeating substring must be a divisor of the length of the input string
  2.Search for all possible divisor of “str.length”, starting for “length/2”

16.（38:Easy）Count and Say

• 该题其实并不难，理解题意后，按照题目中产生序列的规则进行实现即可。编码时，我们设立两个StringBuilder容器类pre和next，pre是我们已知的字符序列，next是我们根据pre产生的下一个字符序列，在扫描pre的过程中，只需要存储最近扫描过的字符past及其出现次数times，当正在扫描的字符与已扫描字符不同时，则按times+past的顺序将两个变量存入next容器并将这两个变量重新初始化即可，按该思路循环直到pre遍历结束且达到第i个序列。（beat 67%）

17.（434:Easy）Number of Segments in a String

• 该题较简单，只需要从头至尾扫描一遍字符串，以空格进行分割，最后返回segments数量即可（beat 100%）。注意不能使用split(" ")方法，因为含有连续的两个空格的字符串“3 2”也会进行成功的分割，产生长度为3的数组，说明其中一个元素是个空格字符串。

18.（443:Easy）String Compression

• 该题需要进行原地in-place操作，其实题目表述不清楚，假设返回值为j，则只需要保证数组的前j个元素是更新后的即可。该题和第16题（38）的思路类似，也是存储当前扫描的字符并且统计当前扫描字符的个数，最后将字符的个数转换为字符串存入数组中即可。

19.（67:Easy）Add Binary

• 该题只需要模拟二进制加法的计算即可，我们设立一个StringBuilder的容器变量来存储运算结果，每次只访问a、b字符串中的一位，并且设立一个进位变量，来判断是否有进位，“a、b字符对应位置的和”以及“进位标志”的运算结果每次均插入StringBuilder容器的0位置（模拟从低位向高位运算）。（beat 86%）

20.（20:Easy）（经典题）Valid Parentheses

• 该题是非常经典的一道题：“括号匹配问题”。解题方法是维护一个堆栈的数据结构，凡是遇到左括号，则压栈；若遇到右括号，在栈非空的情况下出栈并与当前右括号匹配，若不匹配则返回false，否则继续循环，当栈空时，返回false。注意，当输入的括号字符串全部遍历结束后，需要判断栈是否为空，若为空才返回true，否则返回false，因为如串“()[]{”输入到函数中时，在遍历过程中也不会返回false。
• Java中能够实现堆栈的数据结构有很多，Stack容器可能比LinkedList更高效。

21.（686:Easy）（分析稍麻烦）Repeated String Match

• 该题需要事先明确两个问题：1.字符串A是否包含字符串B中的全部种类的字符 2.重复字符串A多次是否能够包含字符串B，最大的重复次数应该设为多少
• 第1个问题：我们只需要设立一个HashSet集合容器，将字符串B中的字符全部存入HashSet中“去重”。接着依次取出容器中不同元素，查看A字符串是否全部包含，若有不包含的，则直接返回-1。注意，判断字符串中是否包含某个“字符”用indexOf()函数，而不是contains()函数，后者只能判断是否含有某个字符串，前者既能判断是否含有字符也可判断是否含有字符串。
• 第2个问题：当A的扩展长度变成B的“2倍+A的长度”时，即为A的最大扩展长度。若此时串B仍不是扩展串extends的子串，则返回-1，否则返回相应扩展倍数。

上面的方法beat 95%，discuss中还有其他思路，下次复习时再看

22.（125:Easy）Valid Palindrome

• 该题考察回文序列，'A'与'a'属于同一个字符，所以需要先将输入的字符串全部变成小写。然后设立两个头尾指针i、j，分别从前向后、从后向前遍历，遇到非字母非数字的字符直接跳过，当遇到字母数字字符时指针停止，比较此刻i、j指针所指字符是否相等，若相等则继续遍历直到两指针相遇返回true，否则返回false。

上面的思路应该比较普遍，可能是采用的数据结构并不高效，只beat 35%，下次复习时需要参看discuss学习一下新的实现方法

23.（680:Easy）Valid Palindrome II

• 该题是第22题（125）的扩展，整体的思路与第22题相同，唯一区别是，我们需要设立一个变量来标记“容错”。当i、j指针第一不匹配时，有两种选择，i指针右移和j指针左移。在实现过程中，实现一个函数专门进行i指针右移的试探，当该函数返回true时，说明i指针右移后可能有与当前j指针所在位置匹配的字符，那么我们将i++，否则j--。需要注意的是，在第一次不匹配时，可能i指针右移或j指针左移均能保证下一次匹配成功，但因为我们首先尝试的是i指针右移，所以并没有进行j左移的操作。但是，在i、j指针左移或右移都可行的前提下，可能局部情况，i指针右移后只能继续匹配少数几个字符，但j指针左移却能匹配剩余所有字符，所以我们应设立变量i0、j0、rightForward来记录第一次不匹配时i、j指针的位置，以及后续采取的指针移动操作，若采取i右移则rightForward=1。当第二次不匹配时，若rightForward=1，我们回复i、j指针的位置，并采取j左移，再次尝试进行匹配；若rightForward=0，说明第一次匹配时就采取j左移操作，直接返回false即可。

上面的思路只beat 3%， 应在下次复习时参考更高效的解题方法

24.（58:Easy）Length of Last Word

• 该题较简单，有两种思路，可以从前往后进行扫描直到找到最后一个单词并计算其长度，但显然效率很低。因为题目只要求我们给出最后一个单词的长度，所以我们可以直接从后往前扫描，当找到倒数第一个单词时，开始长度计数，当遇到单词前的第一个空格时，返回当前长度即可。

25.（14:Easy）Longest Common Prefix

• 该题只需要维护一个容器类StringBuilder作为prefix变量即可，在遍历数组的过程中，只需要比较当前字符串与前缀变量的差异，将不同的部分直接在容器类中删除即可。

上面使用容器类的解法只beat 8%，非常低效，可以使用String变量引用直接进行操作，若prefix部分不重合就直接新建一个subString即可，下次复习时应参看更高效的解题思路

26.（28:Easy）Implement strStr()

• 实际上就是字符串匹配的过程，从母串中寻找是否有子串，有则返回开始出现时的下标，否则返回-1。Java可以直接通过indexOf函数解决该题目，但建议下次复习时参看discuss中的算法解题思路，discuss中都是最简单的字符串匹配过程，都没有使用KMP算法。

27.（537:Medium）Complex Number Multiplication

• complex number是复数，题目的意思是让模拟复数乘法的运算。两复数乘法的运算规则为：(m+ni)*(p+qi) = mp-nq+(mq+np)i。因为输入的复数全是a+bi的形式，所以我们可以使用字符串的split方法将其分为实数域与复数域两个部分，然后按照上面的公式进行相应的运算即可，将结果存入StringBuilder容器，最后返回时转化为字符串。（beat 74%）
• 注意，split()函数的参数是一个正则表达式，因为“+”在正则表达式中有特殊含义，所以当我们希望以“+”进行字符串分割时，需要使用转义字符“\+”（两个\，此处显示不完整）。

28.（791:Medium）（经典题）Custom Sort String

• 当拿到该题时，想到的思路就是，首先根据参照串S，按照顺序将待排序串T中的当前S串所指向的相同字符全部取出并存入StringBuilder容器中，最后再遍历一遍T串，将T串中有但S串中没有的字符按照原顺序插入到容器中最后返回。如S=“cba”，T=“aeabcdcef”，开始先将T串中所有的c字符取出并存入容器，然后是b、a，最后将“edef”插入容器末尾。（beat 56%）
• 也可以使用“哈希表字典”，一方面存储T中的字符种类，一方面也可存储相应字符在T串中出现的个数，该思路效率会更高，只需要遍历一次T串。

discuss中还有利用长度为26的整型数组作为“哈希表字典”，存储T中各个字符的个数，效率应该更高，待下次复习时研究学习

29.（553:Medium）Optimal Division

• 该题要求将输入字符串转化成最大的商，因为除法没有交换律，即“a/b != b/c”，所以为了让商最大，应保证分数的分子尽量大，而使分母尽量小。
• 在给定的输入中，如int[] nums = [a,b,c,d,e,f]，我们在将其转化为除法后得“a/b/c/d/e/f”，那么如何加括号使得该商最大呢？因为每一个输入的数字都是正整数，所以“a >= a/b”，所以为了让整个商最大，我们只能将“a”当做分子，而剩余的"b/c/d/e/f"当做分母，因为要使分母尽量小，根据前面的推理：“b >= b/c”“b/c >= b/c/d”，所以我们只需要保证分母的除法运算是从左向右进行的即可。这样，对于上面的输入，函数的返回值应为“a/((((b/c)/d)/e)/f) （1）”，因为“a/(b/c/d/e/f) (2)”与(1)式的运算结果和运算过程相同，所以我们(2)式即是函数返回的答案。（beat 98%）

<30>.（647:Medium）（非常经典题）Palindromic Substrings

• 该题的思路有三种，下面会分别进行阐述
• 第一种思路（brute force暴力解法）：设置两个指针i、j，初始时刻i=0、j=s.length()-1。思路是循环判断字符串区间[i,j]是否为一个回文序列，然后判断[i,j-1]直到[i,i]；然后让i+1，j重置为s.length()-1，依然按照上面的思路进行判断直到i=s.length()-1。（beat 11.56%）
• 第二种思路（DP动态规划）：定义dp[i][j]：若从i到j的字符串为回文，则为真（1），否则为假（0），那么dp[i][j]为真的前提是：头尾两个字符串相同并且去掉头尾以后的字串也是回文（即dp[i+1][j-1]为真），这里面要注意特殊情况，即：去掉头尾以后为空串或只有单独一个字符，所以如果j-i<3，并且头尾相等，也是回文的。于是便得出下边的关键DP代码：s.charAt(i) == s.charAt(j) && (j - i < 3 || dp[i + 1][j - 1]);（beat 43%）
• DP实现中需要注意：进行for循环时，i需要从s.length()-1开始，直到i=0结束，即i是从后往前进行遍历的，因为在求dp[i][j]的值时需要用到dp[i+1][j-1]的值，例如i=0，j=3，需要判断dp[1][2]的值，但因为i=1的情况还没有遍历，所以i从0往后遍历会出错。
• 第三种思路（由回文中心向两边扩大）：考虑不同的回文中心，然后从中心扩大，求以某个中心来获得的回文个数。通过函数checkPalindrome(s,i,i)判断以当前位置i为中心的**“奇数”长度回文序列个数**，通过函数checkPalindrome(s,i,i+1)判断以(i,j)为中心的**“偶数”长度回文序列个数**。需要注意，s字符串的最后一个字符没有进行奇数长度的回文检查，但其本身单个字符却是奇数回文序列，所以要在for循环退出后将计数器+1。又因为字符串没有s.length()下标，所以最后一个字符不能进行偶数长度的回文序列检查。该思路的示意图如下：

以字符串“aabaa”为例

First Loop(i=0):

奇数回文序列，Palindrome: a (Count=1)

偶数回文序列，Palindrome: aa (Count=2)

Second Loop(i=1):

奇数回文序列，Palindrome: a (Count=3)

偶数回文序列不存在，Palindrome: No Palindrome

Third Loop(i=2):

奇数回文序列，Palindrome: b,aba,aabaa (Count=6)

偶数回文序列不存在，Palindrome: No Palindrome

Forth Loop(i=3):

奇数回文序列，Palindrome: a (Count=7)

偶数回文序列，Palindrome: aa (Count=8)

Count = 9 (For the last character)，因为循环退出条件是i < s.length()-1，而字符串最后一个字符也是长度为1的奇数回文序列。

Answer = 9

31.（609:Medium）（经典题）Find Duplicate File in System

• 该题的题干非常长，但实际上解决起来并不复杂，核心思想是使用Hashtable。
• 我们首先需要维护一个Hashtable变量，它的key为String类型的文件存储内容，value为存储相应内容的文件路径（List列表实现的）。函数的输入参数是一个String[]的字符串数组，而其中的每一个字符串元素的格式为“目录路径 文件名1(内容) 文件名2(内容)...”，那么很显然的，我们需要用split()函数将该字符串以“ ”空格进行分割，那么分割后的数组第一个位置存的是当前的目录路径，后面位置存储的是文件名及内容。所以，我们从分割数组的第二个位置开始循环进行处理，通过indexOf()函数，我们可以获得文件内容前的"("左括号位置，然后通过length()-1可获得“)”右括号位置，从而用subString()函数获得了该文件的内容。然后查找Hashtable中是否有该key（key为文件内容），若存在，则通过与第一个位置的目录路径和由subString获得的当前文件名进行拼接得到当前文件的绝对路径，将该绝对路径存入value列表中；若不存在，则创建相应的key及value列表。
• 最后，通过Hashtable的entrySet()方法快速遍历哈希表，若value列表的大小大于1，则将当前的value列表存入结果集中，最后返回结果集即可。（beat 70%）

32.（22:Medium）（非常经典题）Generate Parentheses

• 该题一种方法是通过暴力搜索，将括号所在位置的所有情况都求解出来，这个过程需要用到DFS深度搜索，当我们将左右括号都使用完毕，最后再判断当前的括号字符串序列是否匹配，若匹配则加入至结果集中。进行括号匹配判断的函数可以借用第20题（20）的isValid()函数。（beat 10%）
• 第二种方法也用到了DFS的思想，不同的是，通过一个巧妙的技巧保证了字符串序列生成过程中左右括号的匹配。因为该题只涉及到小括号，所以该题的括号匹配问题并没有之前的第20题（20）那么复杂，我们只需要保证当前右括号的数量永远小于或等于当前左括号的数量即可，或当已使用的右括号数量小于已使用的左括号数量时我们才可以添加右括号。用代码阐述该思想比较易懂，参考如下：

  public void backtrack(List<String> list, String str, int open, int close, int max){
  //open是当前使用的左括号数量，close是当前使用的右括号数量，max是左右括号可使用的最大数量
     if(str.length() == max*2){	//所有括号都已经用尽
         list.add(str);
         return;
     }
  
     if(open < max)
         backtrack(list, str+"(", open+1, close, max);	//学习递归传递字符串的方式
     if(close < open)	//注意，此处是close < open而不是close < max，从而保证了在添加右括号时当前所有的括号都能匹配
         backtrack(list, str+")", open, close+1, max);
  }    

33.（12:Medium）Integer to Roman

• 罗马数字的基本型为：I=1，V=5，X=10，L=50，C=100，D=500，M=1000，相同的罗马数字最多不能超过三个。所以对于4只能表示为5-1即IV，左减右加，即4=IV。同理，9=IX，40=XL，90=XC，400=CD，900=CM。因为相同的罗马数字最多不能超过三个，所以我们每次循环从最大的罗马数开始算起，若当前的num不能用最大的罗马数字表示时，再试探用次大的罗马数来表示，直到最后num=0。
• 罗马数表示的优先级为：M=1000 > CM=900 > D=500 > CD=400 > C=100 > XC=90 > L=50 > XL=40 > X=10 > IX=9 > V=5 > IV=4 > I=1。只要按照这个优先级进行整型数的表示，最终的结果中相同的罗马数字肯定不超过三个。(beat 29%)

34.（539:Medium）Minimum Time Difference

• 先遍历输入的timePoints列表，通过split()方法将各个时间的小时与分钟数拆开，然后再全部转化成分钟表示的时间并存入一个ArrayList容器中，接着讲ArrayList容器从小到大排序。下一步遍历ArrayList容器，比较相邻两个时间的差值，取所有时间差的最小值。最后，计算容器中最小的时间与最大的时间的差值，因为00:05=24:05，可能24:05与11:55是全局最小的，将该差值与上面遍历完容器的差值做比较，取较小的值返回即可。

上面的方法beat 35%，Discuss中应该还有速度更快的解法，下次复习时再研究

<35>.（583:Medium）（非常非常经典题）Delete Operation for Two Strings

• 该题用DP动态规划思想来进行求解。定义一个二维的dp数组(二维长度是[word1.length()+1][word2.length()+1])，其中dp[i][j]表示word1的前i个字符和word2的前j个字符组成的两个单词的最长公共子序列的长度。注意：dp[i][j]表示word1的前i个字符和word2的前j个字符的最长公共子序列长度，所以当求解dp[i][j]时，实际进行的是“字符串下标”为“i-1”和“j-1”位置的字符比较。
• 首先来考虑dp[i][j]和dp[i-1][j-1]之间的关系，我们可以发现，如果当前的两个字符word1[i-1]和word2[j-1]“相等”，那么dp[i][j] = dp[i-1][j-1] + 1，因为最长相同子序列又多了一个相同的字符，所以长度加1。那么如果word1[i-1]和word2[j-1]两个字符“不相等”呢，我们并不是直接将dp[i-1][j-1]赋值给dp[i][j]，因为与dp[i][j]相邻的状态不是dp[i-1][j-1]，而是dp[i][j-1]和dp[i-1][j]，所以我们会取dp[i][j-1]和dp[i-1][j]中的较大者（这两个变量在求解dp[i][j]时已经求出）。最后dp[word1.length()][word2.length()]就是两字符串的最长公共子序列的长度。
• 因为dp数组的二维长度是[word1.length()+1][word2.length()+1]，所以对dp[i][j]，当i或j有一个为0时，代表比较的两个字符串中有一个是空串，所以此时的数组变量应设为0，即if(i == 0 || j == 0) dp[i][j] = 0。

36.（49:Medium）Group Anagrams

• 该题使用Hashtable结构，key为anagrams字母的排序字符串，value是由相同字母组成的单词集合。因为输入的字符串数组中，含有anagrams，所以对于相同的anagrams，它们的字母是相同的且数量一致，那么我们通过将当前单词的字母按升序排列并再转化成字符串，便可以当成相同系列的anagrams的key键，标识一个集合。最后用entry遍历Hashtable获得结果集返回即可。（beat 86.7%）

37.（17:Medium）Letter Combinations of a Phone Number

• 该题需要用到DFS（Backtracking）的思想，至于为什么想到DFS，正如在Array类问题中总结出的规律，当for循环层数不确定时，我们就可以用DFS方法。在本题中，产生的字符串序列长度和digits字符串长度应该相同，而digits的长度是不确定的，所以我们使用DFS搜索，搜索深度正是digits字符串的长度。
• 注意：电话键盘上的0和1两个按键不对应任何字母，而7和9按键分别对应4个字母。为了在dfs过程中方便获取键盘上的字母，需建立一个二维数组“String[][] map = {{}, {}, {"a","b","c"}, {"d","e","f"}, {"g","h","i"}, {"j","k","l"}, {"m","n","o"}, {"p","q","r","s"}, {"t","u","v"}, {"w","x","y","z"}}”。可以发现，该数组的0下标和1下标均没有任何内容，恰好对应了0键和1键。而在dfs递归过程中，depth的值恰好是当前应该处理的digits字符串中按键字符的下标，当depth=digits.length()时，递归结束，保存当前搜索路径至结果集中并退出。（beat 76%）

<38>.（767:Medium）（非常经典题）Reorganize String

• 该题有几个难点：1.如何判断输入的字符串能重新排成符合条件的串 2.使用什么数据结构可以根据字符出现的顺序将引用变量排序 3.根据什么策略构建符合条件的串 下面根据这三个问题一一解答
• 第1个难点：我们知道，要想保证相邻元素是不同的，那么一定要在相同两元素的间隔中插入不同的元素，如“aaaa”需要在每两个“a”之间插入另外不同的元素，编程“abababa”，也就是说，至少要有“a的数量减1的”其他不同元素存在，才能保证每两个a不相邻。因此，在实现过程中，假如输入的字符串数量长度为n，一旦某个字符的数量大于(n + 1) / 2，说明其他不同字符的数量小于“a的数量减1”，那么一定不满足题意条件，返回空串即可。
• 第2个难点：在之前使用Python做Array类题目时，当进行类排序时，我们需要建立一个比较器，受到Array类题目的启发，该题一定也是从出现频率最高的字符开始操作，然后是次高的元素。显然为每一个字符和其出现频率创建一个类进而排序的时间代价非常高，所以这里借助优先队列实现堆排序，我们可以通过构造一个比较器维护一个大顶堆，那么堆顶便是出现频率最高的字符。下面是进行实现大顶堆的参考代码：

  示例一：
  Comparator<Integer> cmp;///可以new一个比较器;
  cmp = new Comparator<Integer>()
  {
      public int compare(Integer e1,Integer e2)
      {
          return e2 - e1;///重载优先级使其变为大根堆
      }
  };
  Queue<Integer> que = new PriorityQueue<>(cmp);///筛入一个重载比较器使其变为大跟堆

  示例二（AC代码中的示例）：
  PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[1] - a[1]);	//自定义了一个比较器，大顶堆，这里的a、b是长度为2的数组，可从下边向堆里添加元素的结构看出
  for (char c : map.keySet()) {
      pq.add(new int[] {c, map.get(c)});
  }

• 第3个难点：建好了堆以后，如何构造符合条件的字符串呢？根据discuss最高票的答案，思路是：当结果集为空或者结果集的末尾字符与堆顶元素不同时，我们将堆顶元素加入结果集末尾，并将堆顶元素的频率减1后重新加入优先队列中；若结果集不为空且结果集的末尾字符与堆顶元素相同，此时我们从堆中取出频率次大的元素，并将该元素加入到结果集末尾，然后才将频率最大的元素加入结果集末尾，之后将频率最大和次大的频数各减1重新加入堆中。当更新后的频数为0时我们不将该元素加入堆，最终当堆（优先队列）为空时跳出循环返回结果集。（该方法beat 43%）
• 注意：该题开始时，需要通过HashMap统计各个字符的频数，key为字符，value为频数。我们可以通过HashMap的API接口getOrDefault（c，0）函数，来获得字符c的对应频数，当c不在map中时，该函数返回0，若存在则返回对应的实际频数。
• O(n)不需要排序的解法思路：

1. count letter appearance and store in hash[i]
2. find the letter with largest occurence.
3. put the letter into even index numbe (0, 2, 4 ...) char array
4. put the rest into the array

参考链接：浅谈堆以及java优先队列的详细使用

39.（809:Medium）Expressive Words

• 这道题我们首先需要想清楚一个:

1. 如果一个letter不是extendable的说明它连续出现的次数小于3次。那么这样的letter在word中必须要和S中一样。那么我们在s和word中的pointer都++

2）如果是extendable，那么这个letter出现的次数肯定大于2。但是我们判断的时候并不需要算出多少的次数这么复杂。我们只要看S中看i-1，i，i+1这三个位置是不是一样 或者 i-2，i-1，i是不是一样。这里的意思是，如果这两个条件满足一个就说明至少有3个letter连续出现，那么我们只要把S的pointer++就好了。

• 如果以上case不满足，说明这个word不是stretchy的。

<40>.（522:Medium）（非常经典题）Longest Uncommon Subsequence II

• 该题的思路是：首先根据字符串长度值将字符串数组进行降序排列（需要设置一个比较器），如果字符串数组中没有重复的元素，那么最长的字符串一定就是longest uncommon subsequence，但如果输入的字符串数组中存在重复元素且最长字符串也是重复的，那么我们就需要检查其他的次长的字符串。但长度较短的字符串可能是其他长串的子序列subsequence（注意不是子串，二者有区别）。所以，当我们扫描到的某个字符串既没有重复且不是某个长串的子序列，那该串便是最长非公共子序列。接下来分析一下实现过程中的几个关键步骤：
• 如何按照指定策略排列字符串数组：设置一个比较器，代码如下：

  Arrays.sort(strs, new Comparator<String>() {		//自定义了一个比较器，按字符串长度将字符串数组排序
       public int compare(String o1, String o2) {
             return o2.length() - o1.length();
       }
  });

• 如何获取有重复的字符串：设置两个set集合，代码如下：

  private Set<String> getDuplicates(String[] strs) {	//获取有重复串的字符串集合
       Set<String> set = new HashSet<String>();
       Set<String> duplicates = new HashSet<String>();
       for(String s : strs) {
           if(set.contains(s)) duplicates.add(s);
           set.add(s);
       }
       return duplicates;
  }

• 如何判断串b是否为串a的子序列：b串是参照物，当a串中有字符和b串匹配时，指向b串的j指针才+1，指向a的i指针元素不论是否与j指针当前元素匹配，都+1，代码如下：

  public boolean isSubsequence(String a, String b) {		//判断字符串b是否为字符串a的“子序列”
       int i = 0, j = 0;
       while(i < a.length() && j < b.length()) {
           if(a.charAt(i) == b.charAt(j)) j++;	//b串是参照物，当a串中有字符和b串匹配时，指向b串的j指针才+1
              i++;
       }
       return j == b.length();
  }

<41>.（385:Medium）（非常经典题）Mini Parser

• 该题用到的主要思想是Stack堆栈，但因为递归调用的本质实际上就是在内存中维护一个stack，所以该题也可以用递归调用求解。至于该题为何使用堆栈stack或者递归调用求解？原因是：我们可以将该题中所谓的NestedInteger看作一个list，而我们的工作就是进行list的嵌套，所以需要保存外层list和内层list，这时使用Stack或Recursive call很合适。
• 以使用stack堆栈的思路为例进行该题的讲解，至于递归调用的过程可以参看具体的实现代码。我们在解题过程中需要维护两个指针变量l、r分别指向数字串的“起始位置”和“末尾位置+1”，每次我们都会向右移动r指针（r++），当处理完一个数字串后，才更新l指针的值。当r指针所指向的字符为'['时，代表我们将要进入内层的递归，此时需要将上层递归list压栈以便后面进行嵌套操作，然后建立一个新list实例当做内层的list，更新l=r+1；当r指针所指向的字符是']'时，代表该层循环的结束，在将最后一个数字串加入到本层list后，需要将该层的list嵌套进上层的list中；当r指针所指向的字符是','时，通常代表着一个字符串的结束，但若r-1指向的字符是']'时，我们直接将l=r+1不进行其他任何操作，当r-1所指向的字符是数字时，我们将当前锁定的数字加入到本层list中并更新l=r+1；若r指针指向的是数字，则只需要r++即可，l指针因为指向的是数字串的起始位置，所以不做改变。
• 注意：输入的字符串序列中可能包含'-'负号，可能有负数的存在（如：[-1,-10]）。另外，每一个数之间、数和内层list之间都是以','逗号分隔的（如：[3,[1,5]]）。而且，内层list之后可能还会有数字，中间也是用逗号','分隔的（如：[3,[4,1],98]）。

<42>.（227:Medium）（非常经典题）Basic Calculator II

• 由于存在运算优先级，我们采取的措施是使用一个栈保存数字，如果该数字之前的符号是加或减，那么把当前数字压入栈中，注意如果是减号，则加入当前数字的相反数，因为减法相当于加上一个相反数。如果之前的符号是乘或除，那么在遍历输入串时直接从栈顶取出一个数字和当前数字进行乘或除的运算，再把结果压入栈中，那么完成一遍遍历后，所有的乘或除都运算完了，再把栈中所有的数字都加起来就是最终结果了。总结起来就是：栈中保存的是只需要做加法的数字，减去的数字通过变为相反数转化为加法，乘除运算在遍历时就已经完成了计算。（beat 52%）
• 之前按照自己的思路写出的实现代码逻辑上非常冗余，虽然逻辑正确但被OJ判为超时，具体实现可参照代码。
• 注意：我们可以使用Character.isDigit(c)函数来判断该字符是不是一个数字字符，通过c-'0'可以得出该字符代表的int型整数。

43.（678:Medium）（经典题）Valid Parenthesis String

• 该题同样是括号匹配问题的变种，区别在于：1.括号的种类只有一种 2.存在*号，表示任意括号或空字符 因此，结合提到的区别尤其是第二点，我们可以辨析出括号匹配的优先级'('/')' > '*'。
• 我们设立两个堆栈，分别存储“左括号”的下标索引和“*号”的下标索引，这里不向堆栈中压入括号的原因是：1.该题的括号种类只有一种 2.当全部右括号都与左括号匹配结束后，可能还有剩余的左括号，那么此时就需要将“*号”看做右括号与剩余左括号进行匹配，而匹配成功的原则是，待匹配的左括号下标小于当前“*号”的下标。当然，只要将左右括号都匹配成功后，那么便可返回true，因为多余的“*号”可看做空串。
• 逻辑思路为：从左向右遍历输入字符串，当遇到左括号时，将其下标压入括号栈中；当遇到“*号”时，将其下标压入星号栈中；当遇到右括号时，其下标一定大于左括号栈和星号栈的所有下标，所以首先看左括号栈是否为空，不为空则匹配，若为空则看星号栈是否为空，不为空则“*号”此时充当左括号与其匹配，若星号栈为空则当前右括号无法匹配返回false。当按如上策略扫描结束后，所有的右括号应该都已匹配，那么检查左括号栈是否为空，若不为空则取栈顶的元素（栈顶左括号的下标），看星号栈是否为空，此时“*号”充当右括号，若星号栈为空则返回false，否则取星号栈的栈顶“*号”下标，若栈顶“*号”下标大于栈顶左括号下标，则匹配成功，否则匹配失败返回false，按如上策略直到左括号栈为空，才返回true。

44.（556:Medium）（经典题）Next Greater Element III

• 该题和Leetcode Array类31题思路相似，相当于求排列组合序列的下一个排列，区别在于：Lc的31题输入是一个数组返回也是一个数组，而本题的输入是一个整型数，返回也是一个整型数；此外，我们在从后往前找到第一个不是降序的数时，判断条件是大于等于而不是大于，因为可能存在重复元素。（beat 82%）
• 这里总结几个小的技巧：1.输入的整数n转化为字符串数组：(""+n).split("") 2.输入的整数n转化为字符数组(""+n).toCharArray() 这里采用转化为字符数组，因为字符数组在转化为字符串、整数、排序等方面都优于字符串数组（字符串数组处理起来很麻烦） 3.当按题目条件转化后的字符串代表的数字超过了int的最大表示范围2147483648时，应返回-1，而此时用Integer.parseInt()方法会抛出NumberFormatException异常，那么我们便可以根据该异常来判断整数是否超过int最大表示界限，代码如下：

  try {
  	return Integer.parseInt(String.valueOf(number).substring(0, i+1) + String.valueOf(secondSegment));
  }
  catch(NumberFormatException e){		//通过捕捉异常来判断是否越界
  	return -1;
  }

45.（93:Medium）Restore IP Addresses

• 该题使用DFS思想方法，在做题前，我们需要先明确几个ip地址构造的概念：1. 网段数字大小在0-255之间，且网段数字的最大位数只能是3 2.当某一网段的首位是0时，该网段只能为0而不能是01、032等等
• DFS的搜索深度为4，代表着ip地址分为4段。若搜索到的当前起始位置的字符不为'0'时，那么该网段可涵盖的位数可以是1-3位；若搜索到的起始位置为字符'0'时，那么该网段涵盖的位数只能是1位。当我们搜索到最后一个网段时，判断字符串剩余位数是否小于等于3，否则直接退出该搜索路径，因为网段的最大值为三位数255。（该思路beat 76%）
• 注意：异常机制运行起来非常耗时，所以避免用异常机制来判断最后一个网段是否超过255

46.（43:Medium）（经典题）Multiply Strings +++

• 模仿乘法的计算过程，注意处理进位。两个数num1、num2相乘的结果最大位数为len(num1)+len(num2)+1，且该最大位数只有在两因子位数相同时才能达到，所以最后的字符串结果前缀可能有很多'0'，需要进行处理。
• 数字字符可以通过'c'-'0'转化为对应整数值。相乘的结果可以保存在char[]数组中，存取以及修改非常简单，StringBuilder容器不能修改单个字符的值，除非用字符串修改对应位置的字符串，很复杂。
• 注意：当一个非零因子与零因子相乘时，结果只能返回“0”，而不是“000....”。
• 更快捷高效的方法请参考该链接：中文博客解法
• 请参见下面高效的解法，注意到，两数相乘最大的位数为m+n，其中m、n是两数的长度。那么当i位和j位相乘时，只会影响到最终结果i+j位和i+j+1位的值，如下图所示，因此我们可以非常高效的进行字符串的计算：

public String multiply(String num1, String num2) {
    int m = num1.length(), n = num2.length();
    int[] pos = new int[m + n];
   
    for(int i = m - 1; i >= 0; i--) { //当前进行第i位于第j位的运算
        for(int j = n - 1; j >= 0; j--) {
            int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0'); 
            int p1 = i + j, p2 = i + j + 1;  //该次计算只会影响最终结果的p1位和p2位
            int sum = mul + pos[p2];

            pos[p1] += sum / 10;
            pos[p2] = (sum) % 10;
        }
    }  
    
    StringBuilder sb = new StringBuilder();
    for(int p : pos) if(!(sb.length() == 0 && p == 0)) sb.append(p); //if条件语句用于去除前导0
    return sb.length() == 0 ? "0" : sb.toString();
}

上面自己的思路是正确的，但可能是数据结构使用并不恰当只beat 13%，下次复习时应参考discuss看看更高效的实现方法，且乘法除了上面的思路应还有更快的计算方式

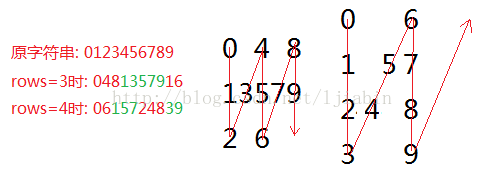
47.（6:Medium）ZigZag Conversion +++

• 首先需要理解，什么是zigZag?简单解释一下，就是把字符串原顺序012345……按下图所示排列：

• 那么依据上面的图示，我们可以按照图中箭头的路径来依次构造新的位置序列。在我的实现解法中，整个序列是保存在LinkedList中的，而LinkedList中又可存储任意个numRows长度的字符数组。在构造好新的序列后，按题目的含义顺序读取出来即可。这里需要注意的是，新的位置序列不一定要和题目中相同，例子如下：

  输入："PAYPALISHIRING"
  题目中给出的排序位置序列如下，最后“按行”读取即为答案：
       P   A   H   N
       A P L S I I G
       Y   I   R            
  我们可以按如下方式进行排列，最后“按列”读取即是答案，在我的实现方法中采用该排列方式：
       P   A   Y
           P
       A   L   I
           S    
       H   I   R
           I
       N   G

上面的思路是正确的，但至少在我的实现解法中并不高效，只beat 1%，可能是一些关键地方的处理方式如数据结构没有选取合适，此外应还有更巧妙的思路来解决该问题，下次复习时应参看discuss学习

• 该题其实是一道类似于找规律的题目，我们首先找出V字型长度，然后将每个字符放置在其对应的位置上，然后从头开始顺序读取字符即可，具体思路请参考：非常清楚的视频讲解

public String convert(String s, int numRows) {
    if(numRows <= 1) return s;
    StringBuilder[] sb = new StringBuilder[numRows];

    for (int i = 0; i < sb.length; i++){
	sb[i] = new StringBuilder();
    }

    //按照ZigZag的顺序来排列字符
    for (int i = 0; i < s.length(); i++){
	int index = i % (2 * numRows - 2); //2 * numRows - 2是V字型循环的长度
	index = index < numRows ? index : 2 * numRows - 2 - index; //这个是根据i在V字型的左侧还是右侧来计算真正的所在行位置
	sb[index].append(s.charAt(i));
    }

    //按顺序读取来组织字符
    for (int i = 1; i < sb.length; i++){
	sb[0].append(sb[i]);
    }
    return sb[0].toString();
}

48.（71:Medium）（经典题）Simplify Path

• 该题实际上实现的程序是一个目录文件系统的访问动态体现，在UNIX系统中，".."是返回上级目录（如果是根目录则不处理）；"."是当前目录不变。因为涉及到目录的向上级跳转或向下级进入，所以使用Stack堆栈是非常恰当的选择，因此可以考虑用栈记录路径名，以便于处理。
• 路径访问的规则是：

1. 重复连续出现的'/'，只按1个处理，即跳过重复连续出现的'/'；
2. 如果路径名是"."，则不处理；
3. 如果路径名是".."，则需要弹栈，如果栈为空，则不做处理；
4. 如果路径名为其他字符串，入栈。这里需要注意：路径名可能为"..."、"...."、".xxx"、"..xxx"、"...xxx"等等

• 最后，再逐个取出栈中元素（即已保存的路径名），用'/'分隔并连接起来，不过要注意顺序。注意输入的路径可能是"/abc"，即最后一个字符不是'/'的情况，所以需要注意边界处理。

上面的思路时间复杂度：O(n)，空间复杂度：O(n)，beat 96.22%

49.（5:Medium）（经典题）Longest Palindromic Substring

• 该题可借鉴第30题（647）的思路，一种是使用"DP动态规划思想"，一种是使用"从中心向两边扩散的思想"。而在本题的实现中，我使用的是DP动态规划思想。
• DP思想对回文序列问题的解决方法及细节原因可参考第30题（647）的笔记，这里只着重说明一下该题DP实现与第30题（647）DP实现的区别：1.本题DP二维数组中存储的是回文序列的长度，而不是i到j字符串是否是一个回文序列，当然若DP[i][j]=0也能说明i到j字符串不是一个回文序列。 2.因为本题函数返回值是一个字符串，而不是最大回文子序列的长度，所以在遍历过程中，需要记录最大回文子序列的长度、该回文序列的起始位置、该回文序列的结束位置，这可以通过长度为3的int数组实现。

50.（3:Medium）Longest Substring Without Repeating Characters

• 该题一种解决思路如下：为了保证字符元素不重复，一定要设置一个set集合存储当前扫描的目标串字符，然后设置一个StringBuilder容器存储当前扫描的目标串，那么扫描的策略是：若当前扫描的字符出现重复时，如："zxcabca"，我们在StringBuilder容器和set集合中删去从当前扫描串起始位置到扫描指针i所指的字符第一次出现的位置中间所有的字符，删除后的串为"bca"，然后重新开始添加后续的扫描字符；若当前扫描的字符没有出现重复时，如已扫描"abcd"，下一个待扫描字符是'e'，那我们将新字符添加进StringBuilder容器和set集合中，并更新最大长度变量maxLen，最后扫描结束返回该值即可。
• the basic idea is, keep a hashmap which stores the characters in string as keys and their positions as values, and keep two pointers which define the max substring. move the right pointer to scan through the string , and meanwhile update the hashmap. If the character is already in the hashmap, then move the left pointer to the right of the same character last found. Note that the two pointers can only move forward.代码如下：

    public int lengthOfLongestSubstring(String s) {
        if (s.length()==0) return 0;
        HashMap<Character, Integer> map = new HashMap<Character, Integer>();
        int max=0;
        for (int i=0, j=0; i<s.length(); ++i){
            if (map.containsKey(s.charAt(i))){
                j = Math.max(j,map.get(s.charAt(i))+1); //该行max函数是该方法的关键
            }
            map.put(s.charAt(i),i);
            max = Math.max(max,i-j+1);
        }
        return max;
    }

上面的思路未参考discuss，只beat 22%，下次复习时再研究学习更高效的解法

51.（722:Medium）Remove Comments

• We only need to check for two things:

1. If we see ‘//’ we stop reading the current line, and add whatever characters we have seen to the result.
2. If we see ‘/’ then we start the multiline comment mode and we keep on ignoring characters until we see ‘/’.
3. If the current character is neither of the above two and the multiline comment mode is off, then we add that character to the current line.

• Once we parse one line (source[i]), then if the mode is off, we add the currently generated line (StringBuilder) to the result and repeat for source[i + 1].

• We need to be careful not to insert empty lines in the result.

以上实现思路直接参考discuss高票答案，beat 100%，下次复习时需要再看

52.（165:Medium）Compare Version Numbers

• 该题需要比较的就是版本号的大小，因为版本号可能会出现类似“1.2.1”的情况，所以我们无法用Float.valueOf()函数将版本号转化为浮点数。
• 这里采用的方法是使用split()函数，将输入的字符串版本号根据"."分成两个字符串数组。然后从数组最左面开始向右扫描，每次比较相同位置的int型数值大小，若相同位置的两个数相等则将数组的下标索引+1继续下一个位置的比较，否则根据大小值返回1或-1。当两个版本数组长度不等时，我们需要继续扫描长度较大的数组的剩余位置数，若剩余位置存在大于0的数，则该较长数组对应的版本号较大，否则两个版本值相等。
• 注意：1.以"."进行字符串的分割时，因'.'在正则表达式中有特殊含义，所以需要使用转义字符，split("\.") 2.version1="1.2" version2="1.2.0"则version1=version2；若version1="1.2" version2="1.2.1"，则version1<version2

上面的思路未看discuss，beat 66%，下次复习时可以参照discuss学习一下新思路

53.（468:Medium）Validate IP Address

• 说一下自己的思路（beat 26%）:首先根据输入串中含有的是“.”还是“:”将输入地址预判为IPV4还是IPV6地址。
• IPV4地址：

1. IPV4只有4个分段
2. IPV4地址中不能含有除数字及'.'外的其他字符,这个判断要放在int值解析前
3. IPV4每一个分段都必须有值
4. IPV4没有前导零,但192.0.0.1允许
5. IPV4每个分段的值为[0,255]且每个分段的长度最大为3

• IPV6地址：

1. IPV6只有8个分段
2. IPV6地址中不能含有除':'、0-9、A-F外的其它字符
3. IPV6每一个分段最长只有4位
4. 不允许出现AB23:0000:87FA简化为AB23::87FA的情况

• 通过以上所有判断的地址才是合理的地址。这里通过正则表达式来判断输入字符串是否含有除合理字符外的其它字符，即看删去其它字符后与原字符串相比是否有变化，代码如下：

  String replacedStr = IP.replaceAll("[^.0-9]","");     //将所有非'.'和数字字符以外的字符用空字符代替（即是删去），看是否存在其他不允许的字符
  if(IP.compareTo(replacedStr) != 0)		
        return "Neither";

  String replacedStr = IP.replaceAll("[^:0-9A-F]","");			//将所有非':'、数字字符、A-F字母以外的字符用空字符代替（即是删去），看是否存在其他不允许的字符
  if(IP.compareTo(replacedStr) != 0)		
        return "Neither";

上面自己的思路只beat 20%+，下次复习时应参考discuss学习更高效解法

54.（91:Medium）（非常经典题）Decode Ways

• 该题一种解法是DFS暴力搜索统计，但显然是超时的。
• 第二种思路是使用DP动态规划思想，使用一个长度为n+1的dp整型数组，那么dp[n]表示字符串的前n个字符的不同解码方式，dp[0]代表前0个字符（即空串）的解码方式，值当然是0，但为了后续递推在这里初始化为1；dp[1]代表前一个字符的解码方式，因为不存在字符对数字0的映射，所以当第一个字符不为0时，dp[1]=1，否则dp[1]=0。基于以上两个初始值，我们便可以得出递推公式：我们要求dp[i]的值（前i个字符的解码方式），那么实际扫描到的字符串中的字符下标位置是i-1，当以一位为一组“Integer.valueOf(s.substring(i-1, i))”的值若在[1,9]之间则dp[i] += dp[i-1]；当以两位为一组“Integer.valueOf(s.substring(i-2, i))”的值若在[10,26]之间则dp[i] += dp[i-2]。最后，dp[n]就是最后返回的结果值。（beat 55%）

该题DP思想参考discuss，但之前我们学习的DP应用通常是在求最值的问题中，所以该题在下次复习时需要再次研究DP的应用场景。此外，也可以参考dicuss中其他的高票答案

55.（151:Medium）Reverse Words in a String

• 不知道该题想要强调什么知识，用String字符串的trim()方法可以除去输入字符串的前导和末尾的空白，然后用split(" ")方法以" "单个空白字符串作为分隔符将字符串分组，从后往前遍历分组，若某个分组的长度为0（空字符串）或含有“ ”则跳过，若是单词则加入StringBuilder容器中，最后返回StringBuilder的字符串结果即可。（beat 88%）

56.（8:Medium）String to Integer (atoi)

• 该题按照题目给出的提示进行编写实现即可。首先用trim()方法去掉输入字符串首尾的空白，然后判断输入串的正负号，接着读取最前侧的整数值，若没有超出int的表示范围则返回原值，若超出就根据正负号返回int的上下限值。（beat 26%）

下次复习时应参考discuss学习更高效的解法

57.（770:Medium）（未做）Basic Calculator IV

该题题干未看懂，且实现代码特别长，等下次有时间再做

58.（632:Hard）（非常经典题）Smallest Range

• 该题自己只能想到brute force的解决方法，没有其他思路，以下陈述参考discuss和网上博客结合自己想法给出：
• Brute force 就是枚举了，每个数组都取出一个数，然后用一个范围包括这些数，在枚举过程中记录最小的range就OK。一种高效的解法是借助优先队列，从每个数组中取出一个放到一个最小堆，用一个范围包括这些数字就是一个合理的range了，每次就从抽出来的数中拿出最小的那个数，然后再加入在那个数组里面后面的那个数，当加不了时就代表循环的结束，在这个过程中收集range最小的答案。注意：因为the range [a,b] is smaller than range [c,d] if b-a < d-c or a < c if b-a == d-c， 我们关注后一种情况，a<c if b-a == d-c，那么[a,b]也小于[c,d]，所以我们每次从优先队列中取出的都是最小的那个数。其他具体实现细节参看代码实现及对应注释。（beat 83%）

该题除了优先队列的思想，还可以借助滑动窗口、hashtable等思想，下次复习时应参考discuss学习

59.（761:Hard）（该题未看懂高级思想方法）Special Binary String

• 题目中对于Special binary string 的定义实际上是这样的：

1. 字符串0和1出现的次数相等
2. 非常关键，字符串开始一定是以1开头，且前缀1出现的次数至少与0出现的次数相等。比如”11100100”是special binary string，因为1出现的次数始终大于等于0。

• 因为是连续两个special binary string位置的交换，所以我们可以遍历S的每个位置，求出每个位置可能的special binary string，接着交换任意两个连续位置的special binary string，取lexicographically最大的。不过这还不算完，注意：At the end of any number of moves，所以还需要迭代一波，直到max不再变化为止，即找到了最大值。

上面的方法其实是最简单最粗鲁的方法，并没有使用任何方法或者技巧，只beat 11%，下次复习时应参考discuss中高票答案，有子结构遍历、将字符串看作山峰等思想可以学习研究

<60>.（730:Hard）（非常经典题）Count Different Palindromic Subsequences

• 该题可以使用递归调用或DP动态规划思想来解决。
• 对于子字符串s[i~j]，可以根据首尾元素分为两种情况进行讨论：s[i]!=s[j] 或者 s[i]==s[j]。我们将s[i~j]的子序列回文个数设为count(i,j)。
• 当s[i]!=s[j]时：count(i,j)=count(i,j-1)+count(i+1,j)-count(i+1,j-1)。（可以理解为两个相交的集合求并，需要去重）
• 当s[i]==s[j]时：

1. 如果si在s[i+1...j-1]中没有出现，那么count(i,j)=2*count(i+1,j-1)+2（乘2是因为在s[i+1...j-1]的所有回文子序列左右两侧各加上s[i]、s[j]会构成新的回文序列，而加2是因为s[i]、s[i]s[j]也是两个单独的回文序列）。
2. 如果si在s[i+1...j-1]中只出现过1次，那么count(i,j)=2*count(i+1,j-1)+1（加1是因为s[i]在求s[i+1...j-1]的所有回文子序列过程中已经计算过，所以只需要加上s[i]s[j]这一个单独的回文序列即可）
3. 如果si在s[i+1...j-1]中出现过2次及以上，那么我们需要找到s[i]在s[i+1...j-1]第一次出现和第最后一次出现的位置l、r，那么count(i,j)=2*count(i+1,j-1)-count(l+1,r-1)（因为s[l]、s[r]已经对s[l+1...r-1]的所有回文子序列进行了一次包裹，所以需减去s[i]、s[j]对s[l+1...r-1]的所有回文子序列包裹的重复部分）

• 上面是递归调用的表示及示意图，DP动态规划的思路与递归调用相同，只不过需要注意从哪开始建立动态规划的base case，即如何保证在计算上层dp值时，底层的dp值一定已经被计算完成。采用的思路是：从len=1即长度为1的子字符串开始，我们从i=0到i=n-1进行计算，然后长度逐渐增长直至len=n。

参考链接：参考的视频教学

<61>.（72:Hard）（非常经典题）Edit Distance

• 该题使用动态规划DP进行解答（最值问题，比较典型的应用），该题也是DP问题相关讲解中的一道经典题目。
• 我们定义dp[i][j]为使word1的前i个字符word1[0..i-1]和word2的前j个字符word2[0..j-1]相等的最少步数。
• 动态规划的base case是dp[i][0] = i; dp[0][j] = j.也就是说，word1[0..i - 1] 转化为 "" 需要至少i步 (deletions)。更一般的情况是我们如何将word1[0..i - 1]转化为word2[0..j - 1]，假设我们已知将word1[0..i - 2]转化为word2[0..j - 2]的方法，即已知dp[i - 1][j - 1]，接下来我们考虑word1[i-1]和word2[j-1]的情况

1. 当word1[i-1] = word2[j-1]时，dp[i][j] = dp[i - 1][j - 1]，我们不必在dp[i - 1][j - 1]的基础上做任何操作

2. 当word1[i-1] != word2[j-1]时，我们需要分以下三种情况进行讨论：

   (1). “Replace” word1[i - 1] by word2[j - 1] (dp[i][j] = dp[i - 1][j - 1] + 1 (for replacement));

   (2). “Delete” word1[i - 1] and word1[0..i - 2] = word2[0..j - 1] (dp[i][j] = dp[i - 1][j] + 1 (for deletion));该情况较难理解，可以认为我们删除了word1[i-1]元素后，设法使word1[0..i-2]转化为word2[0..j-1]。

   (3). “Insert” word2[j - 1] to word1[0..i - 1] and word1[0..i - 1] + word2[j - 1] = word2[0..j - 1] (dp[i][j] = dp[i][j - 1] + 1 (for insertion)). 这种情况也可以理解为，我们在word1[i-1]后插入了一个word2[j-1]元素后，只需要设法使word1[0 ..i-1]转化为word2[0..j-2]即可。

上面均是以word1为参照物，当然也可以以word2为参照物，道理相似。

• 总结起来，DP方法的递推式为：

1. dp[i][0] = i;
2. dp[0][j] = j;
3. dp[i][j] = dp[i - 1][j - 1], if word1[i - 1] = word2[j - 1];
4. dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i - 1][j] + 1, dp[i][j - 1] + 1), otherwise.

<62>.（115:Hard）（非常经典题）Distinct Subsequences

“When you see string problem that is about subsequence or matching, dynamic programming method should come to your mind naturally. ”

• 使用DP动态规划思想，设置动态规划数组dp[i][j]，表示S串中从开始位置到第i位置与T串从开始位置到第j位置匹配的子序列的个数。如果S串为空，那么dp[0][j]都是0；如果T串为空，那么dp[i][j]都是1，因为空串为是任何字符串的字串。
• dp[i][j] = dp[i-1][j] when s[i-1] != t[j-1] or dp[i][j] = dp[i-1][j] + dp[i-1][j-1] when s[i-1] == t[j-1],We first keep in mind that s is the longer string [0, i-1], t is the shorter substring [0, j-1]. We can assume t is fixed, and s is increasing in character one by one (this is the key point).
• The first case is easy to catch. When the new character in s, s[i-1], is not equal with the head char in t, t[j-1], we can no longer increment the number of distinct subsequences, it is the same as the situation before incrementing the s, so dp[i][j] = dp[i-1][j].
• However, when the new incrementing character in s, s[i-1] is equal with t[j-1], which contains two case:

1. We don’t match those two characters, which means that it still has original number of distinct subsequences, so dp[i][j] = dp[i-1][j].（这种情况我们当作s[i-1]与t[j-1]不相等，即不计入不保留当前的s[i-1]）
2. We match those two characters, in this way. dp[i][j] = dp[i-1][j-1].（这种情况保留计入s[i-1]，例如s="ab",t="ab"，那么此时"ab"包含一个"ab"，而"a"也只包含一个"a"，所以dp[i][j]=dp[i-1][j-1]） Thus, including both two case, dp[i][j] = dp[i-1][j] + dp[i-1][j-1]

很奇怪正确的解法被OJ提示超出内存限制，且将dp数组降为一维后仍然无法ac

该题当s[i-1]=t[i-1]时，处理的思路比较绕，下次复习时应该再仔细思考并与同学进行讨论

<63>.（87:Hard）（非常经典题）Scramble String ++++

• 该题有两种解法，一种是Recursive call递归调用(相当于暴力解法)，另一种是DP动态规划解法。
• 以递归调用为例，其实也是暴力遍历，把s1，s2分别分成两部分，判断s1的两部分和s2的两部分是否分别可以交换相等。简单的说，就是s1和s2是scramble的话，那么必然存在一个在s1上的长度l1，将s1分成s11和s12两段，同样有s21和s22.那么要么s11和s21是scramble的并且s12和s22是scramble的；要么s11和s22是scramble的并且s12和s21是scramble的。所以我们用for循环来寻找合适的划分，并且递归调用之。（beat 96%）

该题还有DP的解法，但做题时没有参考，下次复习时应仔细学习研究discuss中dp的思路

64.（591:Hard）（非常经典题）Tag Validator ++++

• 按照题目中标签规则进行实现，利用两个String函数**startsWith()和indexOf()**来求起始和结束标签。具体的解法及思路参看代码实现和相关注释。（beat 85%）

<65>.（336:Hard）（非常经典题）Palindrome Pairs ++++

• 该题有很多思路，这里以Hashmap哈希表查找的思路为例（beat 85%）。brute force暴力解法会被OJ判为“超时”，这也是该题被归为hard类的可能原因。

总共可分为四种情况：

There are several cases to be considered that isPalindrome(s1 + s2):

1、如果字符串有为空的，则任意一个对称字符串与之可以拼凑

Case1: If s1 is a blank string, then for any string that is palindrome s2, s1+s2 and s2+s1 are palindrome.

2、如果一个字符串是另一个字符串的反转，则可以拼凑

If s2 is the reversing string of s1, then s1+s2 and s2+s1 are palindrome.

3、如果字符串s1的前n个字符是对称的，即s1[0,n），并且s1[n,len)与s2是互为相反的，则(s2,s1)构成对称字符串

If s1[0:cut] is palindrome and there exists s2 is the reversing string of s1[cut+1:] , then s2+s1 is palindrome.

4、如果字符串s2的后几个字符是对称的，即s1[n,len),并且s1[0,n)与s2是互为相反的，则(s1, s2)构成对称字符串

Case 4: Similiar to case3. If s1[cut+1: ] is palindrome and there exists s2 is the reversing string of s1[0:cut] , then s1+s2 is palindrome.

• 为了方便对可能的匹配串进行直接的查找，使用哈希表的“一次存取”性质，假如“abc”串存在，则返回“abc”串的下标索引，否则为空说明不存在可连接为回文序列的另一个子串。

该题除了hash表以外，还有trie结构、set集合可解决该问题，下次复习时应参考discuss研究学习

66.（76:Hard）（非常非常经典题）Minimum Window Substring ++++

• 该题一种思路基本与第58题（632）Smallest Range相同，使用优先队列存储t串中所有的字符及对应下标，每次取出队头的下标最小的值，比较范围后并对其更新。需要注意的一点是，可能s="aabbbs" t="abb",那么我们需要存储t串中两个'b'字符的下标索引，且在更新第一个'b'字符时，下一个插入优先队列的'b'字符应在当前第二个已知'b'字符的下标索引之后，即s串中应更新第一个b字符的下标为4而不是3。因此，我们需要用一个HashMap存储字符与其所有当前已知下标索引值。（可能因为数据结构比较复杂，所以运行非常耗时 仅beat 8%）
• 第二种思路利用字符的ASCII码值，用int数组搭建一个简单的hash映射表，并且模拟滑动窗口的移动规律进行实现，没有借助java的高级数据结构，具体思路如下（beat 61%）：

首先分析条件：

1.T中字符可能有重复；

2.S包含T的条件：S中包含所有T中的字符；T中所有字符出现次数都不大于S中对应字符出现次数；

根据以上，算法思路为：

首先对T中出现的字符以及出现次数做统计，之后查找S中是否有对应字符，以及对应字符出现次数是否不小于T中出现次数。

其次设计数据结构：

为了统计字符串中出现的字符以及次数，使用其ASCII码作为Hash表索引，利用一个长度为128的数组（英文字母ASCII码值不超过128）来存储出现字符，以及字符出现次数。例如如果字符'A'出现了3次，则统计数组c['A']=3（相当于c[65]=3，因为'A'的ASCII码是65）。

之后设计算法细节：

1.设置2个指针start和end，分别指向S中包含T的最小Window的开始和结束位置。

2.由于要找到包含T的最小Window，所以需要遍历整个字符串。又由于时间复杂度为O(n)，所以只能遍历一次。

3.为了比较S中字符出现次数与T中字符出现次数，用一个标志count来计数。count表示T的长度，当S中找到的字符次数都与T中字符次数对应相等，并且count等于T的长度，则可知找到了包含T的Window。

4.为了判断Window是否最小，用一个minwin来存储找到的Window。

算法大致过程如下：

1.遍历T，将T中字符出现次数存入数组ta[]；新建数组sa[]存储S中字符出现次数；

2.设置指针start和end，都指向S开始位置；

3.end向后遍历，若遇到的字符在ta[]中的值不为0（即T中存在的字符），则有两种情况：一、sa[]中该字符值等于ta[]中该字符值，则说明该字符已经找够，不需要再找，则忽略该字符，继续遍历；二、sa[]中该字符值小于ta[]中该字符值（sa[]中该字符值可能为0，即未出现过的字符），则说明该字符还未找全，将sa[]中该字符值加1，count加1，继续遍历。若遇到的字符在ta[]中的值为0，忽略该字符，继续遍历；

4.当count值等于T的长度，则说明已经找到了T中所有元素，end暂停遍历；此时关注start，在此时的start处或者start向后一段内，可能都是T中不存在的字符，但由于这些字符未计入count值，所以是否包含这些字符不影响判断条件；但是为了找到最小的Window，需要start向后遍历，将T中不存在的字符都排除，找到T中存在的第一个字符位置，即找到了一个包含T的Window；将此时的Window长度与minwin长度比较，若小于minwin长度，说明找到了更小的Window，更新minwin为当前找到的Window；

5.找到一个Window后end继续遍历。每当end后移一步，就考察start处字符，若start处字符次数大于T中该字符次数，则start后移，若start处字符不存在T中，start也后移，直到找到包含T的最小Window，再进行记录。

6.直到end遍历到S的结尾位置，算法结束。

• 第二种思路具体的细节可参看代码实现。

字符串问题的模板解法参考链接：对大部分string的子串问题的模板解法，一定要看！

67.（97:Hard）（非常非常经典题）Interleaving String

“When you see string problem that is about subsequence or matching, dynamic programming method should come to your mind naturally. ”

• 这是一道关于字符串操作的题目，要求是判断一个字符串能不能由两个字符串按照他们自己的顺序，每次挑取两个串中的一个字符来构造出来。该题使用DP动态规划解法。像这种判断能否按照某种规则来完成求是否或者某个量的题目，很容易会想到用动态规划来实现。（beat 57%）
• 维护一个二维数组，res[i][j]表示用s1的前i个字符和s2的前j个字符能不能按照规则表示出s3的前i+j个字符，如此最后结果就是res[s1.length()][s2.length()]，判断是否为真即可。接下来就是递推式了，假设知道res[i][j]之前的所有历史信息，我们怎么得到res[i][j]。可以看出，其实只有两种方式来递推，一种是选取s1的字符作为s3新加进来的字符，另一种是选s2的字符作为新进字符。而要看看能不能选取，就是判断s1(s2)的第i(j)个字符是否与s3的i+j个字符相等。如果可以选取并且对应的res[i-1]j也为真，就说明s3的i+j个字符可以被表示。这两种情况只要有一种成立，就说明res[i][j]为真，是一个或的关系。
• 所以递推式可以表示成：dp[i][j] = (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1)) || (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)); .注意两种情况需要用括号括起来单独考虑。
• 时间上因为是一个二维动态规划，所以复杂度是O(m*n)，m和n分别是s1和s2的长度。最后就是空间花费，可以看出递推式中只需要用到上一行的信息，所以我们只需要一个一维数组就可以完成历史信息的维护。

<68>.（214:Hard）（非常非常经典题）Shortest Palindrome

In this problem, we don’t need to use KMP to match strings but instead we use the lookup table in KMP to find the palindrome.

• 先讲一下思路：让在前面补一些字符使得给定的字符串变成回文，观察可以发现我们需要添加多少个字符与给定字符串的前缀子串回文的长度有关。也就是说去掉其前缀的回文子串，我们只需要补充剩下的子串的逆序就可以了，例如：aacecaaa，其前缀的最大回文子串是aacecaa，剩下了一个a，因此我们只需要在前面加上一个a的逆序a就行了。再例如abcd，其前缀的最大回文是a，因此剩下的子串就为bcd，所以需要在前面加上bcd的逆序，就变成了dcbabcd．所以这样问题就转化为求字符串的前缀最大回文长度。简单来说，就是找到从第一个字母起始的最长的回文字符串，然后把剩下的倒置加到前面，就得到了最短的回文字符串。
• 对于具体实现，一个naive的方法是先判断整个字符串是否回文，否的话再判断前n-1个子串是否回文，这样依次缩减长度，直到找到一个回文子串就是最大的前缀回文子串．这种方法简单粗暴，容易理解和实现，如果在面试中要求不是很严格的情况下说不定可以过关, 反正总比不会好点^.^．其时间复杂度是O(n!)．但该暴力解法无法通过OJ，我们得想出更高效的解法。
• 首先确认一点基本知识，如果某个字符串str是回文的，那么str == reverse(str)。因此，将s逆转之后拼接在s后面，即news=s+reverse(s)，该新字符串news首尾相同的部分，即为s中以s[0]为起始的最长回文子串pres。只不过这里我不用上述的遍历来求最长回文前缀串，而用类似KMP算法求next数组来做。在KMP算法中求next数组就是s自我匹配的过程，next[i]的值就表示s[i]之前有几个元素是与s开头元素相同的。我们还需要在这两个字符串之间加一个冗余字符，因为形如aaaaa这种字符串如果不加一个冗余字符最大前缀和后缀会变大（We add “#” here to force the match in reverse(s) starts from its first index）所以news=s+"#"+reverse(s)。因此，next[news.size()]的值就表示news中首尾相同的部分的长度。（s的前缀必然是一个回文串（长度可能为1），任务就是求这个回文串的最长长度，因此拼接之后的 s+"#"+s.reverse 必然有公共前缀后缀）

参考链接：

1. DISCUSS：详细讲述KMP算法及该题应用
2. 中文博客：Shortest Palindrome@LeetCode（以及关于KMP的理解）

The only purpose of ‘#’ is to reset the length of matched prefix.并不是很理解“#”的作用，下次复习时再请教同学

<69>.（10:Hard）（非常非常经典题）（面试必考题）Regular Expression Matching

• 该题刚开始设想是从左到右依次读取，先读取正则表达式，然后再解析字符串，虽然能解决大部分正常的解析式，但对如s="aaa" p="abac*a"的测试例无法通过，如果仍按照该思路，只能利用“递归调用”来解决。实际上，该题有两种正确的解题思路：DP或回溯(递归调用)。下面我将其他博客上的内容及个人理解摘录至此：

思路

这里面最复杂的操作是”*”，这是个很可恶的操作，因为你永远不知道它多长。但是有一点，”*”不会单独出现，它一定是和前面一个字母或”.”配成一对。看成一对后”X*”，它的性质就是：要不匹配0个，要不匹配连续的“X”。题目的关键就是如何把这一对“X*”放到适合的位置。

考虑一个特殊的问题：

情况1： s = “aaaaaaaaaaaaaaaa” p = “aaa”

情况2： s = “aaaaaaaaaaaaaaaa” p = “a*ab*”

在不知道后面的情况的时候，我如何匹配a*？

1. 最长匹配。显然不合适，这样后面的a就无法匹配上了

2. 匹配到和后面长度一样的位置，比如情况1，就是留3个a不匹配，让后面3个字母尝试去匹配。这样看似合适，但是遇到情况2就不行了。

3. 回溯，尝试每种"*"的情况，看哪种情况能成功，如果其中出现了问题，马上回溯，换下一种情况

思路1——回溯(beat 65%)

如果"*"不好判断，那我大不了就来个暴力的算法，把“*”的所有可能性都测试一遍看是否有满足的，用两个指针i,j来表明当前s和p的字符。我们采用从后往前匹配，为什么这么匹配？ 因为如果我们从前往后匹配，每个字符我们都得判断是否后面跟着“*”，而且还要考虑越界的问题。但是从后往前没这个问题，一旦遇到“*”，前面必然有个字符。

• 如果j遇到"*"，我们判断s[i] 和 p[j-1]是否相同：如果相同我们可以先尝试匹配掉s的这个字符，i-1，然后看之后能不能满足条件，若满足条件，则继续递归调用下去，否则马上回溯，改变递归调用的方向，即不匹配s的这个字符，j-=2 (跳过"*"前面的字符)。

• 如果j遇到的不是"*"，那么我们就直接看s[i]和p[j]是否相等，不相等就说明错了，返回。

• 再考虑退出的情况：如果j已经<0了说明p已经匹配完了，这时候，如果s匹配完了，说明正确，如果s没匹配完，说明错误；如果i已经<0了说明s已经匹配完，这时候，s可以没匹配完，只要它还有"*"存在，我们继续执行代码（即正则表达式未解析的部分必须凑成"X*"才能返回true，*可以取0个X）。

思路2——DP（没有进行代码实现，具体的程序看参考链接的博客即可）

DP的话，肯定要用空间换时间了，这里用 monkeyGoCrazy 的思路：用2维布尔数组，dp[i][j]的含义是s[0..i] 与 s[0..j]是否匹配，即正则表达式的前j个字符是否能正确解析字符串的前i个字符。

1. p.charAt(j) == s.charAt(i) : dp[i][j] = dp[i-1][j-1]
2. If p.charAt(j) == ‘.’ : dp[i][j] = dp[i-1][j-1];
3. If p.charAt(j) == ‘*’:
   here are two sub conditions:
      if p.charAt(j-1) != s.charAt(i) : dp[i][j] = dp[i][j-2] //in this case, X* only counts as empty
      if p.charAt(i-1) == s.charAt(i) or p.charAt(i-1) == ‘.’:
           dp[i][j] = dp[i-1][j] //in this case, X* counts as multiple X（X可以算作1个或多个，j没变，i减小）
           dp[i][j] = dp[i][j-2] // in this case, X* counts as empty（i没变，j减2）

这里用的布尔数组比较巧妙。前两种情况好理解，如果匹配成功就维持之前的真假值。程序的目的是看真值能不能传递下去。如果遇到第三种情况，我们就看哪种情况有真值可以传递，就继续传递下去。

我用excel自己跑了下代码，画了一下示意图，下面橘黄色表示正常匹配了，蓝色表示“*”匹配空串。可以看出真值是如何传递下去的。

参考链接：该题非常清楚的中文解析

70.（32:Hard）（非常非常经典题） Longest Valid Parentheses

• 该题是普通括号匹配问题的扩展，因此我们自然要想到使用Stack堆栈的数据结构。但该题关键是要分辨出有效的括号串，即有效串何时开始何时结束。
• The workflow of the solution is as below.(beat 22%)

1. Scan the string from beginning to end.

2. If current character is ‘(’,push its index to the stack.

   If current character is ‘)’ and the character at the index of the top of stack is ‘(’, we just find amatching pair so pop from the stack. Otherwise, we push the index of ’)’ to the stack.

3. After the scan is done, the stack will only contain the indices of characters which cannot be matched. Then let’s use the opposite side - substring between adjacent indices should be valid parentheses.

4. If the stack is empty, the whole input string is valid. Otherwise, we can scan the stack to get longest valid substring as described in step 3.

• stack的代码参考如下，注意stack中存储的是数组下表索引，因为只有'('或')'，没有其他类型的括号，没必要再stack中存储他们的字符，只用存储其位置即可：

public int longestValidParentheses(String s) {
	int n = s.length(), longest = 0;
	Stack<Integer> st = new Stack<>();
	for (int i = 0; i < n; i++) {
        if (s.charAt(i) == '(') 
            	st.push(i);   //注意stack中存的是数组下标索引
        else {
                if (!st.empty()) {
                    if (s.charAt(st.lastElement()) == '(') 
                    	st.pop();
                    else 
                    	st.push(i);
                }
                else 
                	st.push(i);
            }
        }
		
	if (st.empty()) 
		longest = n;
	else {
            int a = n, b = 0;
            //取两个无效括号中间所夹的有效括号的长度
            while (!st.empty()) {
                b = st.pop();
                longest = Math.max(longest, a-b-1);
                a = b;
            }
            longest = Math.max(longest, a);
        }
        return longest;
}

该题还可以用DP动态规划来求解，下次复习时参考discuss学习研究

71.（273:Hard）（经典题）Integer to English Words

• 该题只需要以1000为一个单位分块进行处理即可，可以借助递归调用。（beat 88%）
• 实现时采用一个技巧，将数字对应的英文字母存储在一个数组成员变量中，保证数字对应的下标索引的元素就是相应的英文单词。注意，1-9的英文是必须存储的，10-19也需要特殊进行存储（含eleven、twelve、-teen），此外还有20、30...90的英文单词。

72.（30:Hard）（非常非常经典题）Substring with Concatenation of All Words

• 该题一开始想到的方法是通过DFS构造所有的可能的单词拼接（全排列），然后利用indexOf()函数去搜索是否含有当前拼接的单词串。但因为java函数的输入数据结构是数组，实现比较复杂，耗时比较长，感觉并不可行。
• 正确的思路是利用滑动窗口（看做双指针）和HashMap键值映射。我们用一个hash表map来存储words数组中每个单词的词频，考虑到可能words数组中有多个“apple”。设立变量n存储单词的个数（words数组的长度），变量m存储每个单词的长度（题目已交代单词的长度均相同），然后维护一个滑动窗口的左边界i，i值从0到s.length() - n * m，一个符合条件的可以囊括所有单词的滑动窗口长度应为n*m，所以若i到达s.length - n * m后还往右继续移动，就一定不能囊括所有单词了。此外，还需维护一个滑动窗口的右边界j（初始化为i），然后从j开始向后取长度为m的子串，判断是否为合格的单词，若“是”，则将j向右移动m个单位；若“否”，则将窗口的左边界i右移一个单位，重新从窗口长度0开始试探。当窗口囊括了所有words中的单词后则将当前的窗口起始位置i加入结果集中。（beat 40%，具体实现细节看代码）

该题还有DP的方法，可能更高效，下次复习时再研究学习

73.（44:Hard）（非常非常经典题）（面试必考题）Wildcard Matching

• 该题其实与第69题（10）思路非常相近，甚至还更简单，当然开始想到的就是在第69题（10）已通过的**递归调用（DFS）**代码的基础上进行一些小的修改。为了尽可能降低耗时，在正则表达式中读到''时，应该尽可能的先匹配''后第一个字母字符，这样才能减少递归的分支（具体可以参看代码），但无奈没有通过OJ，超时了，可能是因为回溯分支过多。
• 第二种方式是对递归调用的改进，思路基本相同，只不过我们不进行递归向下搜索，而是维护两个变量match、starIdx起到记录回溯的作用。该优化后的回溯方法时间复杂度为O(n)，空间复杂度为O(1)，beat 90%+。与未优化的递归DFS相比：每一个‘’会产生一些分支，用没有优化过的递归是所有‘’产生的分支都会被回溯直到发现match为止；而用这个方法只会回溯最后一个‘*’的分支，不会继续往上。把这个结构看成一棵树，这个方法只回溯最后一层。（具体思路可以参看代码及其注释）
• 同第69题（10）题一样，该题也可以用动态规划DP来解决（时间和空间复杂度均为O(m*n)），思路更加简单清晰，但我并没有进行实现，具体代码参看参考链接。这里重点解释DP中的一个递推式

  if(p.charAt(j - 1) == '*')   
        dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
  1. dp[i-1][j] means that the * matches a 1 character (most recent) in S and we can continue to use * to 
     match more previous characters（因为j指针位置没变，但i指针一直往前推进）
  2. dp[i][j-1] means that the * matches no character in S（因为尽管j指针向右移动了一位，但是i指针并没有因匹配成功而右移）

• 比较好的，理解该题的DP思路讲解：

dp[i][j]: true if the first i char in String s matches the first j chars in String p

Base case:
    origin: dp[0][0]: they do match, so dp[0][0] = true
    first row: dp[0][j]: except for String p starts with *, otherwise all false
    first col: dp[i][0]: can't match when p is empty. All false.
Recursion:
    Iterate through every dp[i][j]
    dp[i][j] = true:
        if (s[ith] == p[jth] || p[jth] == '?') && dp[i-1][j-1] == true
        elif p[jth] == '*' && (dp[i-1][j] == true || dp[i][j-1] == true)，注意是第j个字符等于'*'
        -for dp[i-1][j], means that * acts like an empty sequence.
        eg: ab, ab*
        -for dp[i][j-1], means that * acts like any sequences
        eg: abcd, ab* 
Start from 0 to len
Output put should be dp[s.len][p.len], referring to the whole s matches the whole p 

参考链接：

1. 递归调用原理及DP原理解释

2. 改进的回溯代码

3. 改进的回溯原理讨论

4. 改进的回溯视频讲解

74.（65:Hard）（奇葩题）Valid Number

• 该题我使用的是正则表达式的解法，除了正则表达式的构造非常麻烦以外（"[-+]?(\d+\.?|\.\d+)\d*(e[-+]?\d+)?"），思路都非常清晰，但效率较低，只beat 8%。

discuss中还有利用DFS有限状态机的思路，效率应更高，下次复习时再研究

75.（68:Hard）Text Justification

• 基本的实现题，并不考察什么算法思想。首先分两大类，末行和非末行；然后末行所有单词间放一个空格，最后面补充空格；非末行再分两类，如果只有一个单词就靠左放，右边补空格；如果有多个单词，即计算有几个间隔num和几个多余的空格extra（除每两个单词间一个空格外多余的），每个间隔再多方extra/num个，前extra%num个间隔再多放个空格。(beat 99.76%，具体实现思路参看代码)

• 该题貌似是google面经题，题出的不好，但可能也会考。

参考视频：Text Justification 中文讲解视频

该题并没有仔细做，直接粘贴答案。此外，该题好像还能用DP解决，下次复习时再仔细研究

76.（564:Hard）（经典题）Find the Closest Palindrome

• **如何将一个不是回文数的数变成回文数呢？**我们有两种选择，要么改变左半边，要么改变右半边。由于我们希望和原数绝对差最小，肯定是改变低位上的数比较好，所以我们改变右半边，那么改变的情况又分为两种，一种是原数本来就是回文数，这种情况下，我们需要改变中间的那个数字，要么增加1，要么减小1，比如121，可以变成111和131。另一种情况是原数不是回文数，我们只需要改变右半边就行了，比如123，变成121。那么其实这三种情况可以总结起来，分别相当于对中间的2进行了-1, +1, +0操作。先取出包括中间数的左半边，比如123就取出12，1234也取出12，然后就要根据左半边生成右半边。
• 上面只考虑了最后结果是与输入数字位数相同的情况，如果最终的回文数和输入数字位数不同，一定是 999....999 或 1000...0001，所以我们把这种情况也考虑进去，最后我们在candidates集合中找出和原数绝对差最小的那个返回，注意要略过原数。（beat 28%，具体实现思路可以参看代码）

77.（126:Hard）（太复杂未做）Word Ladder II

下次复习时再研究学习

78.（833:Medium）（非常经典题）Find And Replace in String

• 该题需要用到一个小技巧：如果我们从前向后replace字符串，那么之后的字符下标索引会被改变，所以我们将索引index降序排列，那么先处理靠后位置的字符串并不会影响之前下标的索引。

79.（929:Easy）Unique Email Addresses

• 用String的split()函数以符号'@'作切分，来处理local name和domain name

80.（482:Easy）License Key Formatting

• 首先遍历一遍输入字符串，将'-'删去且将其转换为大写字符。然后判断第一个group的字符数是否少于K，若小于的话需要注意特殊处理。

81.（395:Medium）（非常经典题）Longest Substring with At Least K Repeating Characters

• In each step, just find the infrequent elements (show less than k times) as splits since any of these infrequent elements couldn't be any part of the substring we want.
• 此外以出现频率少于k的字符为分界点，利用backtracking进行求解

82.（809:Medium）（非常经典题）Expressive Words

• 题目说了一大堆，简单理解就是，给出一个长字符串S，以及一个words list。Words 里面每个word，可以通过扩展当前的char，来尝试构造S。extend的规则是，S中的char，必须连续出现>=3 才可以extend。问，words里面会有几个word 能够extend到S中。
• 需要注意的是，S中可能的字符有的可能只出现了3次，有的可能出现了大于3次，需要分别处理。具体可以参看如下的代码及注释。

public int expressiveWords(String S, String[] words) {
    int res = 0;
    for (String W : words) if (check(S, W)) res++;
    return res;
}
    
public boolean check(String S, String W) {
    int n = S.length(), m = W.length(), j = 0;
    for (int i = 0; i < n; i++)
        if (j < m && S.charAt(i) == W.charAt(j)) j++; //如果当前j没有到达word 末尾。且 当前word的char == S的char
        else if (i > 1 && S.charAt(i) == S.charAt(i - 1) && S.charAt(i - 1) == S.charAt(i - 2)); //当前word的char ！= S的当前word char，可能S中当前字符重复出现超过3次
        else if (0 < i && i < n - 1 && S.charAt(i - 1) == S.charAt(i) && S.charAt(i) == S.charAt(i + 1)); // 当前字符可能出现3次
        else return false; //当前word的字符与S中对应字符不可能匹配，或者S中当前的字符只出现了两次且与word中字符不匹配
    return j == m; //看看是不是当前的word也遍历完毕
}

83.（819:Easy）Most Common Word

• 该题逻辑非常清晰的一个思路是，首先将字符串转化为小写字母之后，用正则表达式将字符串分解成一个个word，然后统计他们出现的频率。接着遍历banned数组，将banned words从map中删去，确保剩余的单词都是有效的，最后找出出现频率最高的单词并返回。

84.（796:Easy）Rotate String

• We can easily see whether it is rotated if B can be found in (A + A). For example, with A = "abcde", B = "cdeab", we have

“abcdeabcde” (A + A)
  “cdeab” (B)

B is found in (A + A), so B is a rotated string of A.

85.（824:Easy）Goat Latin

• 严格按照题意实现即可

//下面是非常concise的code，应该学习
    public String toGoatLatin(String S) {
        Set<Character> vowel = new HashSet<Character>();
        for (char c : "aeiouAEIOU".toCharArray()) vowel.add(c);
        String res = "";
        int i = 0, j = 0;
        for (String w : S.split(" ")) {
            res += ' ' + (vowel.contains(w.charAt(0)) ? w : w.substring(1) + w.charAt(0)) + "ma";
            for (j = 0, ++i; j < i; ++j) res += "a";
        };
        return res.substring(1);
    }

86.（921:Medium）（非常经典题）Minimum Add to Make Parentheses Valid

• Loop through the input array.

    if encounter '(', push '(' into stack;
    otherwise, ')', check if there is a matching '(' on top of stack; if no, increase the counter by 1; if yes, pop it out;
    after the loop, count in the un-matched characters remaining in the stack.

• Discuss还有代码更加精简的版本，但我认为提交的代码较容易理解，所以下次复习时需要学习一下更精简的算法。该题之所以不能遍历一次字符串计算出左括号和右括号的数量，然后返回它们的差值，是因为例如"()))(("的字符串是无法用这种方法求出来的。

public int minAddToMakeValid(String S) {
    Deque<Character> stk = new ArrayDeque<>();
    for (char c : S.toCharArray()) {
        if (c == ')' && !stk.isEmpty() && stk.peek() == '(') { stk.pop(); } // pop out matched pairs.
        else { stk.push(c); } // push in unmatched chars.
    }
    return stk.size();
}

87.（709:Easy）（经典题）To Lower Case

• 利用ASCII码进行大小写的转化即可char-'A'+'a'.

88.（710:Easy）Unique Morse Code Words

• 按题目所给的映射关系进行拼接即可，将转化后的字符串存入set中去重，最后函数返回set的size。

89.（937:Easy）Reorder Log Files

• 该题的思路：先把两类字符串分开，然后对纯字母的那些进行排序， 最后合并结果就好。
• 另外一个关注点是：复习Comparator类的构造

90.（271:Medium）（非常经典题）Encode and Decode Strings

• 在encode时，先存储string的长度，再存储string字符串本身。我们虽然以'/'字符作为size和string的分割符，但并不会影响string中含有'/'，因为我们在读取完size后，会跳过string的真正内容。

    // Encodes a list of strings to a single string.
    public String encode(List<String> strs) {
        StringBuilder sb = new StringBuilder();
        //str里也可以含有'/'字符，但因为我们存储了str的长度，所以能够cover这种case
        for(String s : strs) {
            sb.append(s.length()).append('/').append(s);
        }
        return sb.toString();
    }

    // Decodes a single string to a list of strings.
    public List<String> decode(String s) {
        List<String> ret = new ArrayList<String>();
        int i = 0;
        while(i < s.length()) {
            int slash = s.indexOf('/', i);
            int size = Integer.valueOf(s.substring(i, slash));
            i = slash + size + 1; //i指向的应该是当前字符串的下一个字符串的size的起始索引
            ret.add(s.substring(slash + 1, i));
        }
        return ret;
    }

91.（1108:Easy）Defanging an IP Address

public String defangIPaddr(String address) {
    return address.replace(".", "[.]");
}

92.（890:Medium）（经典题）Find and Replace Pattern

• 将所有的word和pattern都转化成对应的基本pattern，例如aab->112，ksc->123，然后再进行比较即可。