Math (Java) - ShuweiLeung/Thinking GitHub Wiki

Let's write down all of 12's factors:

2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12

As you can see, calculations of 4 × 3 and 6 × 2 are not necessary.

1.（9:Easy）Palindrome Number

• 很简单，考察回文序列的定义，可以把int转成String，然后将其倒置reverse后，比较其与原数是否相等，相等返回true，否则返回false。

2.（728:Easy）Self Dividing Numbers

• 只需要让区间内的数字分别除以它的各个digits即可，注意若某一位为0则直接跳过该数。

3.（812:Easy）Largest Triangle Area

• 用三个for循环，在最内层算出三个点构成的三角形的边，然后根据面积公式求解即可。

4.（258:Easy）Add Digits

• 该题只需要将int数转化为char数组，然后返回求和直到结果为个位数即可。
• 该题还有O(1)的解法，具体解释和实现参看链接：O(1)-time O(1)-space 1 Solution

5.（171:Easy）（经典题）Excel Sheet Column Number

• 该题类似于26进制数转化为10进制数，需要用到幂函数。

6.（168:Easy）（经典题）Excel Sheet Column Title

• 本质是10进制数转为26进制数，注意：由于下标从1开始而不是从0开始，因此要减一操作。

10进制数向其他进制数的转化还不熟悉，需要强化练习

7.（598:Easy）（经典题）Range Addition II

• 一开始按照题目创建一个全0的M矩阵，然后对其进行操作，虽然思路正确，但其实没有理解问题的本质，当矩阵大小为最大时超时。
• 其实我们可以发现，值最大的元素个数，其实就是所有操作所包含的最小面积的矩形大小，因为所有操作的元素增加范围都是从0开始的。因此我们只需要求这个最小矩形的边界即可（实现过程参考代码）。

8.（453:Easy）（经典题+）Minimum Moves to Equal Array Elements

• 该题用了一个逻辑反转的技巧，我们将n-1个数字加一，相当于将剩余的那个数减一。因此，最优的方法是将n-1个数都减至n个数中的最小值。

9.（415:Easy）Add Strings

• 该题和String类Medium难度43题multiply strings的思路一样，维护一个进位即可

10.（202:Easy）Happy Number

• 循环对每个digit求平方后取和，直到和为1时返回true。对于非happy number，我们需要建立一个set集合，存储每一个digit平方和的结果，若某结果重复出现则说明有循环，返回false。

11.（326:Easy）（公式转换）Power of Three

• 利用log函数，以log以10为底来模拟log以3为底：log10(n)/log10(3) = log3(n)，若结果为整数说明n是3的幂次。

该类型题最快的方法是利用位运算，下次复习时再研究学习

12.（231:Easy）Power of Two

• 思路同第11题（326）。

13.（263:Easy）Ugly Number

• 只需要重复测试当前的n值是否能被2、3、5其中之一除尽，若某一刻2、3、5都不能除尽则返回false，若最终的n值=1则返回true。

14.（645:Easy）（经典题）Set Mismatch

• 该题与Array类中Medium类第43题（565）非常相似，因为数组中的元素值在[1,n]之间，所以对于长度为n的数组，对应的数组下标在[0,n-1]之间。从左至右遍历数组，当nums[abs(nums[i])-1]为正数时，将其置为对应的相反数；若为负数，则说明之前有相同的元素值abs(nums[x])=abs(nums[i])已将其置为负，那么此时该负数的下标索引+1就是重复数字。之后再次遍历数组，剩余唯一的正数对应的下标+1就是缺失的证书。

15.（367:Easy）（经典题）Valid Perfect Square

• 该题的解法有很多，第一种当然是最容易想到的brute force暴力解法，可惜超时。
• 第二种解法利用一条数学性质：完全平方数是一系列奇数之和，时间复杂度为O(sqrt(n))。例如：

1 = 1

4 = 1 + 3

9 = 1 + 3 + 5

16 = 1 + 3 + 5 + 7

25 = 1 + 3 + 5 + 7 + 9

36 = 1 + 3 + 5 + 7 + 9 + 11

....

1+3+...+(2n-1) = (2n-1 + 1)n/2 = n*n

• 第三种解法是二分查找，时间复杂度为O(logN)，在这里直接贴上代码：

public boolean isPerfectSquare(int num) {
   long left = 0, right = num;
   while (left <= right) {
       long mid = left + (right - left) / 2, t = mid * mid;
       if (t == num) return true;
       else if (t < num) left = mid + 1;
       else right = mid - 1;
   }
   return false;
}

16.（172:Easy）（经典题）Factorial Trailing Zeroes

• 0总是由2*5产生的，而2的个数总是多于5的个数，因为从1到n，至少有n/2个偶数，但是5的倍数的数却很少，因此我们只需要统计5的个数。那么如何在log数量级时间复杂度内计算出5的个数呢？我们需参考以下例子推算：

例1

n=15。那么在15! 中 有3个5(来自其中的5, 10, 15)， 所以计算n/5就可以。

例2

n=50。与例1相同，计算n/5，可以得到10个5，分别来自其中的5, 10, 15, 20, 25, 30, 35, 40, 45, 50，但是在25=5*5中其实是包含2个5的，如果只做50/5的计算，我们忽略了25提供的另外一个5，这一点需要注意。因此，我们还需求50/25，得到由25, 50的因子25提供的额外的一个5（此处除以25的结果是2不是4，是因为一个25因子提供的其中一个5已经在n/5的过程中考虑在内）。

所以除了计算n/5， 还要计算n/5/5, n/5/5/5, n/5/5/5/5, ..., n/5/5/5,,,/5直到商为0，然后就和，就是最后的结果。

这里5的计算规律还需在下次复习时与同学进行讨论

17.（441:Easy）（经典题）Arranging Coins

• 该题的本质是：1+2+3+4+...+m = (m+1)m/2，求最大的m值，使(m+1)m/2恰好小于等于n。因为m*m可能大于int的最大表示范围，所以我们用long来进行计算，最后返回时只需要强制转换一下类型即可。若从m=1开始尝试，则会“超时”，所以我在这里采用二分查找的思路，当low=high时，判断(low+1)*low/2是否大于n，若大于n则返回low-1，否则返回low。

discuss中也有brute force的解答，但我自己尝试不能通过测试例，不知道为什么

18.（507:Easy）Perfect Number

• 一种方法是求出num的所有因子，但不能使用brute force的暴力方法，会超时。为了避免time out，我们需要让i从1开始测试到num/2，若num%i=0，那么与i对应的另外一个因子是num/i，当num/i >= i时说明因子还不会出现重复，所以可以向因子集合中持续添加，但若num/i < i，说明因子开始与之前结果对称出现，即之前i是3，num/i是4；现在i是4，num/i是3，此刻应退出循环，已找齐num的所有因子。（其实i*i < num的i值才可能是num的因子）

上面的方法只beat 9%，下次复习时需要参看discuss学习更高效的解法

19.（633:Easy）（经典题）Sum of Square Numbers

• 思路同第18题（507）类似，i从0开始增大，当i * i < num时才进入循环，然后计算sqrt(num - i * i)，得到的值若为一个整数则返回true，否则i+1进行下一次循环。当sqrt(num - i * i) < i时，退出循环返回false，道理同第18题（507）中所述一样。（beat 41%）
• 该题也可用双指针法进行求解，更高效beat 90%+，初始值low = 0，high = sqrt(num)，cur = left * left + right * right，当cur < num, left++；若cur > num，right--；若cur = num，返回true。代码如下：

public boolean judgeSquareSum(int c) {
  if (c < 0) {
      return false;
  }
  int left = 0, right = (int)Math.sqrt(c);
  while (left <= right) {
      int cur = left * left + right * right;
      if (cur < c) {
          left++;
      } else if (cur > c) {
          right--;
      } else {
          return true;
      }
  }
  return false;
}

20.（400:Easy）（经典题）Nth Digit

• 先判断第n位是在几位整数上，然后判断这个几位整数具体是哪个整数，然后返回对应整数的对应位，思路直接参考下面的代码：（beat 99%）

public int findNthDigit(int n) {
      int len = 1;        //从个位数开始尝试
	    long count = 9;     //从1-9开始算起
      int start = 1;      //个位数的起始值是1

	    while (n > len * count) {
		    n -= len * count;
		    len += 1;       //尝试2位数、3位数...
		    count *= 10;    //尝试10-99（90个数），100-999（900个数）...
		    start *= 10;    //2位数的起始值是10，3位数的起始值是100...
	    }

	    start += (n - 1) / len;     //定位第n位是在哪一个整数上
	    String s = Integer.toString(start);     
	    return Character.getNumericValue(s.charAt((n - 1) % len));      //返回对应整数上的对应位
}

21.（69:Easy）（经典题）Sqrt(x)

• 该题和第15题（367）的第三种解法**“二分查找”的思路相同，只需要一直比较mid*mid与x的值即可。需要注意**，为了避免平方值越过int的上界，这里我们将low、high、mid都设为long型。

22.（204:Easy）（非常经典题）Count Primes

• 该题最直观的方法，就是暴力尝试从2到n-1的每一个数，查看是否能被n除尽，显然该法是超时的。
• 第二种方法运用了小的技巧，我们知道，一个数的因子，我们只需要遍历从i=1到i=sqrt(n)，即可全部得出，对大于sqrt(n)的因子，可通过其对应的另一半因子得到n/i(i < sqrt(n))。基于此，我们尝试从i=2到i=sqrt(n)的每一个数，若存在某个i能被n整除则n为非质数，否则n为质数。虽然时间复杂度为O(sqrt(n))，但也超时。
• 正确的高效的解法是埃拉托斯特尼筛法Sieve of Eratosthenes。这个算法的过程如下图所示，我们从2开始遍历到根号n，先找到第一个质数2，然后将其所有的倍数全部标记出来，然后到下一个质数3，标记其所有倍数，一次类推，直到根号n，此时数组中未被标记的数字就是质数。（时间复杂度为O(nloglogn)，空间复杂度为O(n)，beat 82%）

23.（7:Easy）Reverse Integer

• 该题比较简单，通过将其转化为字符串然后进行反转即可。需要注意：1. x若为负数则需要注意**“负号”** 2. 当数字反转的结果超过int的表示上下界时，用Java的异常机制进行捕捉判断。

24.（413:Medium）Arithmetic Slices

• 该题一开始考虑用滑动窗口的思路去求解，但仔细分析后发现其实没有那么复杂。我们只需要用指针i从左到右遍历数组，把每一个位置都当作slice (P, Q)的起点P，然后先进行长度为3的sequence试探，判断是否为arithmetic slice，若是，记录当前相邻元素的差值diff，继续进行长度为4、5...的sequence试探直到不满足条件为止，然后i+1，进行下一个位置P的尝试。（beat 100%）

25.（462:Medium）Minimum Moves to Equal Array Elements II

• 该题与Minimum Moves to Equal Array Elements I有一些区别，II中可以一次增加1个元素的值，但I中只能一次增加n-1个元素的值。因此我们不能采取与I相同的策略，而应该寻找nums中的中位数，即离所有数最近的一个数作为变化标准

26.（535:Medium）Encode and Decode TinyURL

• 该天是一个设计类题目，想Accepted很容易，关键是借助HashMap如何做好key:longUrl到value:shortUrl的映射。这里个人认为最好是使用hash函数，那么如何设计hash函数，设计一个合理的不重复的hash函数就是关键。

27.（319:Medium）（经典题）Bulb Switcher

• 一开始尝试用哈希表（HashSet）来做，表中存储的只有亮着的灯泡，但超时。当然实例化一个数组进行求解也是可行的，但是当输入的n很大时，初始化数组的开销一定很大，所以不必尝试一定是超时的。
• 正确的解法是从数学或规律的角度来解决：当一个灯泡被执行偶数次switch操作时（包括0次）它是关着的，当被执行奇数次switch操作时它是开着的，那么这题就是要找出哪些编号的灯泡会被执行奇数次操作。
• 现在假如我们执行第i次操作，即从编号i开始对编号每次+i进行switch操作，对于这些灯来说，如果其编号j（j=1,2,3,⋯,n）能够整除i，则编号j的灯需要执行switch操作。具备这样性质的i是成对出现的，比如：j=12时，编号为12的灯，在第1次，第12次；第2次，第6次；第3次，第4次一定会被执行Switch操作，这样的话，编号为12的等肯定为灭。即，j的所有因子都会被执行操作选中，而所有因子是不重复且是成对出现的。
• 但是当完全平方数36就不一样了，因为他有一个特殊的因数6，这样当i=6时，只能被执行一次Switch操作（完全平方数两个因子相同，只被执行一次，6=6），这样推出，完全平方数一定是亮着的，所以本题的关键在于找完全平方数的个数 sqrt(n)。

28.（672:Medium）Bulb Switcher II

• 纯数学题。 如果我们使用了 button 1 和 2, 其效果等同于使用 button 3 。类似的..

1 + 2 --> 3, 1 + 3 --> 2, 2 + 3 --> 1

所以，只有 8 种情形。

All_on, 1, 2, 3, 4, 1+4, 2+4, 3+4

即有 8 种独立的按钮操作（假设原来的状态是 on, on, on, on） :

1 (off, off, off, off)

2 (on, off, on, off)

3 (off, on, off, on)

4 (off, on, on, off)

1 + 4 (on, off, off, on)

2 + 4 (off, off, on, on)

3 + 4 (on, on, off, off)

1 + 2 + 3 == 3 + 3 (on, on, on, on)

该题下次复习时还需和其他同学讨论，感觉考察的知识有点偏

29.（781:Medium）（经典题）Rabbits in Forest

• 感觉该题有点像找规律的题，首先是受到题目中样例的启发。我们举个例子就能说明该问题的本质：假如answers = [3,3]，那么我们可以认为有一个大小为4的兔子群体，回答的都是该同一群体中的兔子；当answers = [3,3,3,3]时，该大小为4的群体均已参与了回答；当answers = [3,3,3,3,3]，我们首先可以拿前面的规律进行化简，首先将前4个回答的兔子归为一个群体，那么剩余的最后一个兔子只能是另外一个大小为4的群体中的兔子，这样，兔子的总数最少就为4+4=8。
• 基于上例，我们需要用一个HashMap统计各个回答与对应的回答数，当“回答+1”大于等于回答的兔子数时，我们可以将其同一归为大小为“回答+1”的兔子群体，当“回答+1”小于回答的兔子数时，我们就需要迭代的将回答的兔子数减去“回答+1”的大小值，同时在总兔子数上加“回答+1”的大小值，直到回答的兔子数小于等于0。

30.（789:Medium）Escape The Ghosts

• 该题看似复杂，其实并不难，题目中有两个关键点：1. 幽灵可以在我们移动的同时也进行移动，当然，幽灵也可以选择不动 2. 当幽灵和我们同时到达target时，也被视为游戏失败
• 基于上述分析，只要幽灵可以先一步或同时到达target位置并且保持不变，游戏一定是失败的。所以，只要存在一个幽灵的位置比源点(0,0)位置距target近，那么游戏一定失败。这里需要注意：距离的衡量方式并不是直线距离（sqrt((a1-a2)^2+(b1-b2)^2)），而是曼哈顿距离(abs(a1-a2)+abs(b1-b2))。因为，每次移动均是水平或纵向的移动，而不能沿对角线直接移动，所以用直线距离衡量并不准确。

31.（343:Medium）（非常经典题）Integer Break

• 该题有两种方法，一种是dp动态规划思想，另一种是数学推导的方法。
• 动态规划思想：我们维护一个dp数组，dp[i]表示数字i分解后数字乘积的最大值。对每一个数字i，我们将其从j=1开始分解为j与i-j，并求得分解后数值乘积，取其中的最大值。递推公式为dp[i] = Math.max(dp[i], (Math.max(j,dp[j])) * (Math.max(i - j, dp[i - j])))，可以这样理解：i被分为j与i-j，而j又可以被分为多个数的和，它们的积为dp[j]；同样i-j也可以被分为多个数的和，它们的积为dp[i-j]；所以Math.max(j,dp[j])是选取较大的j，Math.max(i - j, dp[i - j])是选取较大的i-j。
• 数学推导思想：这道题给了我们一个正整数n，让我们拆分成至少两个正整数之和，使其乘积最大，题目提示中让我们用O(n)来解题，而且告诉我们找7到10之间的规律，那么我们一点一点的来分析：

正整数从1开始，但是1不能拆分成两个正整数之和，所以不能当输出。

那么2只能拆成1+1，所以乘积也为1。

数字3可以拆分成2+1或1+1+1，显然第一种拆分方法乘积大为2。

数字4拆成2+2，乘积最大，为4。

数字5拆成3+2，乘积最大，为6。

数字6拆成3+3，乘积最大，为9。

数字7拆为3+4，乘积最大，为12。

数字8拆为3+3+2，乘积最大，为18。

数字9拆为3+3+3，乘积最大，为27。

数字10拆为3+3+4，乘积最大，为36。

....

• 那么通过观察上面的规律，我们可以看出从5开始，数字都需要先拆出所有的3，一直拆到剩下一个数为2或者4，因为剩4就不用再拆了，拆成两个2和不拆没有意义，而且4不能拆出一个3剩一个1，这样会比拆成2+2的乘积小。那么这样我们就可以写代码了，先预处理n为2和3的情况，然后先将结果res初始化为1，然后当n大于4开始循环，我们结果自乘3，n自减3，根据之前的分析，当跳出循环时，n只能是2或者4，再乘以res返回即可。

32.（357:Medium）（非常经典题）Count Numbers with Unique Digits

• 该题有两种方法，一种是类似于DP动态规划的解法（其实可以不使用DP），另一种是DFS深度搜索的解法。
• 类DP解法：该方法较易理解，简单来说就是从最高位开始算起，因为n位数的最高位不能是0，所以有1-9共9个数字可以选择，而次高位除去最高位数字，加上0的话有9个数字可供选择安放，同理次次高位有8个数字...而11位数必定有两位数字出现重复，因为单个位的数字只有0-9共10个数字。具体的推导见下：

This is a digit combination problem. Can be solved in at most 10 loops.

When n == 0, return 1. I got this answer from the test case.

When n == 1, _ can put 10 digit in the only position. [0, ... , 10]. Answer is 10.

When n == 2, _ _ first digit has 9 choices [1, ..., 9], second one has 9 choices excluding the already chosen one. So totally 9 * 9 = 81. answer should be 10 + 81 = 91

When n == 3, _ _ _ total choice is 9 * 9 * 8 = 684. answer is 10 + 81 + 648 = 739

When n == 4, _ _ _ _ total choice is 9 * 9 * 8 * 7.

...

When n == 10, _ _ _ _ _ _ _ _ _ _ total choice is 9 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1

When n == 11, _ _ _ _ _ _ _ _ _ _ _ total choice is 9 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 * 0 = 0。当某数字有11位的时候必定重复

• DFS深度搜索：DFS其实一开始并不容易想到，为了使用DFS，我们需要维护一个长度为10的布尔数组used，它的数组下标为0-9代表某一位上可以安放的数字，当当前位要放置i的时候，used[i]置为true，代表已经使用过，那么当再往深层搜索时，我们只能在下一位上放置之前没有出现过的数字（used[i]为false的数字i)，而在计数时，我们用count变量保存当前层的数字"ab"和以"ab"为前缀的其他位数不重复的数字"abXYZ..."。因为搜索同时是横向进行的，当我们在某一层置used[i]=true并调用递归函数后，需要再将used[i]置为false，因为在下一次"循环"(注意不是"递归"),我们要置used[i+1]为true从而保持搜索深度相同。（具体实现请参看代码实现及注释）

33.（592:Medium）Fraction Addition and Subtraction

• 该题其实难度并不大，关键就是将分数从字符串中分离出来。我在这里是用两个ArrayList容器分别存储分子和分母，相同位置i的分子和分母组成对应的分数。同时，减一个分数看作加上一个负的分数，那么运算可以大大化简。我们只需要将所有分母相乘后计算所有对应倍数的分子的和，然后利用辗转相除法找到最大公因数化简后即可得到答案。

34.（423:Medium）（经典题）Reconstruct Original Digits from English

• 该题需要用到一个小技巧：

zero: Only digit with z

two: Only digit with w

four: Only digit with u

six: Only digit with x

eight: Only digit with g

对于one, three, five, seven, nine，The odd ones for easy looking, each one's letters all also appear in other digit words.因此我们需要先将偶数digit算出来，然后再依次算奇数digit。

• so we only need to count the unique letter of each word, because the input is always valid.（具体思路可以参看代码实现）

35.（593:Medium）（经典题）Valid Square

• 该题需要借用向量的性质：对于vector1 = (x1,y1) vector2 = (x2,y2) 若两向量平行：x1 * y2 = x2 * y1； 若两向量垂直：x1 * x2 + y1 * y2 = 0。
• 因此我们首先确定四边形的四边相等后，利用上述向量的性质进行进一步判断。
• 注意，若以p1点作为基准，我们需要将p4替换为p1的对点，即p1p4边是四边形的最长对角线。（beat 92%）

36.（640:Medium）Solve the Equation

• 该题思路比较清晰，只需要根据'='将输入的等式划分为两部分，分别统计各部分的x系数和实数值，最后分别进行对比即可。（beat 90%）
• 注意：当x的系数为1时，i=j，应显式设置数字为1，而不是通过截取子串的方式获得系数。

37.（264:Medium）（非常非常经典题）Ugly Number II

• 从题目例子中我们可以发现，已给出的前10个ugly numbers均是质数2、3、5的倍数，于是我们可以推断，ugly numbers可以分为三个序列的结合：

(1) 1×2, 2×2, 3×2, 4×2, 5×2, …

(2) 1×3, 2×3, 3×3, 4×3, 5×3, …

(3) 1×5, 2×5, 3×5, 4×5, 5×5, …

We can find that every subsequence is the ugly-sequence itself (1, 2, 3, 4, 5, …) multiply 2, 3, 5.

• 像merge-sort一样，我们每次选取三个序列中最小的数放到ugly number的第i个位置上，最终返回第n个位置的数即是答案。
• 需要注意：上面序列中2、3、5质数乘以的因子并不是连续递增的，即7、11、13等因子不能与2、3、5相乘，因为会引入除2、3、5以外的其他因子，从而导致乘积的结果不是ugly number。因此，质数2、3、5只能与之前已经求出的ugly数字（相当于上面序列的乘积因子）相乘，这样才能同时保证ugly number是递增的，而且每次选取的ugly number也是当前最小的。

个人认为该题非常好，具体的实现细节请参看代码及其注释

38.（313:Medium）（非常经典题）Super Ugly Number

• 该题与第37题（264）Ugly Number II的思路基本一抹一眼，只是各序列指向ugly数组的指针从变量改为数组，具体细节请参看第37题（264）的笔记及该题代码。

39.（279:Medium）（非常经典题）Perfect Squares

• 该题使用动态规划进行求解，关键是找到递推式，对待求的n，可以分为n-ii和ii两个数，而n-ii可以由dp[n-ii]个平方数求得，而ii可以由1个平方数即i求得，而dp[n]初始化为n（即当作由n个1组成），可得递推公式为dp[n]=min(dp[n],dp[n-ii]+1)（对所有的i*i<=n中的i进行尝试）。（beat 37%）

该题除了动态规划外，还可以用“四平方和定理”进行求解，且除了该动态规划思路外，还有其他的可能更高效动态规划思路，下次复习时需要研究学习

40.（372:Medium）（经典题）Super Pow

• 该题需要用到一个数学性质：(a*b) % k = (a%k)(b%k)%k => a^1234567 % k = (a^1234560 % k) * (a^7 % k) % k = (a^123456 % k)^10 % k * (a^7 % k) % k
• 上面的式子看起来有点复杂，用f(a, b) 表示 a^b % k，那么上面的式子可以简化为 f(a,1234567) = f(a, 1234560) * f(a, 7) % k = f(f(a, 123456),10) * f(a,7)%k。那么我们可以递归的调用f函数，直到f(a,b)可以返回一个可计算的常数为止。

41.（368:Medium）（非常非常经典题）Largest Divisible Subset

• 该题使用的是DP动态规划思想，需要注意上边的总结感想中提到的DP注意事项：某个状态的dp值一旦确定不能更改。且该题中dp数组是count[]，count[i]代表nums[i]在可能的largest subset中出现的位次。为了说明该题的解决原理，我们以下例作为说明（beat 71.2%）：

nums = [1, 2, 4, 6, 8]

count=  1  2  3  3  4  这里6其实是在1、2、6这个subset中，而8是在1、2、4、8这个subset中

pre  =  -1  0  1  1  2   这里pre数组其实是为了维护subset的一个次序，相当于将subset前后元素用一根线串起来

count[i]的值实际上是nums[i]对nums数组中“所有”小于nums[i]的值进行整除尝试得出的，并随着除数numsj的增大，从而更新count[i]的值，即若nums[i]%nums[j]=0，则count[i]=max(count[i],count[j]+1)（等号右边的count[i]是“之前”算出的nums[i]所在集合,count[j]+1是“当前”算出的nums[i]所在集合）

而pre数组存在的意义实际上是为后面返回ArrayList数组提供了方便。pre=-1，作为nums[i]是当前集合中第一个元素的标志。

此外，为了在一次遍历后直接取得count[]数组中最大的值，我们需要维护两个变量maxCount（largest divisible subset的大小）和对应的数字下标索引index（最大整除集合中最后一个数字的位置）。

• 为了按上面的思路进行求解，我们需要将nums数组进行升序排序，以便对所有的j<i，nums[j]<nums[i]。

42.（223:Medium）（非常经典题）Rectangle Area

• 该题直观上就知道答案应该是“两矩形的面积和-重叠矩形面积”。但第一个想法就是根据两个矩形的相对位置进行分类讨论，对不同情况的位置由两个对角坐标进行表示并进行面积的求解，当然该方法是暴力求解，虽然也能通过OJ，分类讨论的情况很多，非常易出错（具体分类情况请参看代码实现）。
• 高效的思路是根据重叠矩形四边的位置关系确定其面积。如下图，重叠矩形的四边位置坐标分别为：left = max(A, E)、right = Math.min(C, G)、top = min(D, H)、bottom = max(B, F)。从而重叠矩形的面积overlap = (right - left) * (top - bottom)。

43.（396:Medium）（经典题）Rotate Function

• 该题有两种方法，一种是根据题意进行粗暴的解法，一种是根据规律推算。
• 粗暴解法：按照题目，每次顺时针移动一个元素并计算最新的F值，然后更新已知F的最大值。效率很低，只beat 4%。
• 规律推算：下面是逻辑推导出的公式，具体实现参看代码。（beat 99%）

F(k) = 0 * Bk[0] + 1 * Bk[1] + ... + (n-1) * Bk[n-1]

F(k-1) = 0 * Bk-1[0] + 1 * Bk-1[1] + ... + (n-1) * Bk-1[n-1]

       = 0 * Bk[1] + 1 * Bk[2] + ... + (n-2) * Bk[n-1] + (n-1) * Bk[0]

两式相减得：

F(k) - F(k-1) = Bk[1] + Bk[2] + ... + Bk[n-1] + (1-n)Bk[0]

              = (Bk[0] + ... + Bk[n-1]) - nBk[0]

              = sum - nBk[0]

将F(k-1)移到等式右边得：

F(k) = F(k-1) + sum - nBk[0]

那么只要求得Bk[0]，我们便可以求得递推式

k = 0; B[0] = A[0];

k = 1; B[0] = A[len-1];

k = 2; B[0] = A[len-2];

...

基于上面公式推导，只要我们算出F(0)便可递推出F(1)...F(n-1)

44.（397:Medium）（非常经典题）Integer Replacement

• 该题其实最快捷的方法是bit位位移，主要思想是：**如果这个数偶数，那么末位的bit位一定是0；如果一个数是奇数，那么末位的bit位一定是1。对于偶数，操作是直接除以2。对于奇数的操作:如果倒数第二位是0，那么n-1的操作比n+1的操作能消掉更多的1；如果倒数第二位是1，那么n+1的操作能比n-1的操作消掉更多的1。
• 对于上面思想的解释，其实主要是尽量花费少的步数使n变为1，当然最快的方法是n以及n/2、n/4、n/8...均是偶数，那么折半的速度一定是最快的**。但在计算过程中n可能是奇数，导致n+1、n-1对2的折半计算次数可能不同。如15->16->8->4->2->1、15->14->7->6->3->2->1，两者递减速度不同。该题的解决办法就是执行一条能让n被尽量多的2整除的路径，当n为奇数时，n-1或n+1除以2后仍是偶数的路径才是应该被选择的。
• 上面两点各对应着一种方法，我在实现过程中只提交了第二种思想的实现（具体细节请参看代码），而对第一张bit位移的操作并没有进行编码，但具体代码可以参看参考链接。

参考链接：Bit Manipulation

45.（60:Medium）（非常经典题）Permutation Sequence

• 该题和Leetcode Array类Medium第31题思路类似，完全借鉴该题的思路即可，从最小的1234...序列开始推算。该思路虽然能通过OJ，但耗时非常长，仅能beat 0%。

下次复习时应参看discuss中更高效的方法

46.（2:Medium）（经典题）Add Two Numbers

• 该题其实就是一个链表处理的问题，一开始尝试将链表的值转化为整型，但无奈test case给的值对应的int、long均越界溢出。于是，只能尝试像String类中某个字符串加法的题目一样，进行字符串的加法运算，维护一个carryBit的进位变量，然后进行计算。可能数据结构选取不合适，只能beat 5%。

该题可能一边读取链表，一边进行加法计算，这样的效率会更高。下次复习时应参看discuss中解法，看看是否有该边读取边计算思路

47.（365:Medium）（经典题/脑经急转弯题）Water and Jug Problem（该题完全没思路，直接看的答案，下面是分析）

• 这是一道脑筋急转弯题。有一个容量为3升和一个容量为5升的水罐，问我们如何准确的称出4升的水。我想很多人都知道怎么做，先把5升水罐装满水，倒到3升水罐里，这时5升水罐里还有2升水，然后把3升水罐里的水都倒掉，把5升水罐中的2升水倒入3升水罐中，这时候把5升水罐解满，然后往此时有2升水的3升水罐里倒水，这样5升水罐倒出1升后还剩4升即为所求。这个很多人都知道，但是这道题随意给我们了三个参数，问有没有解法，这就比较难了。
• 这道问题其实可以转换为有一个很大的容器，我们有两个杯子，容量分别为x和y，问我们通过用两个杯子往里倒水，和往出舀水，问能不能使容器中的水刚好为z升。那么我们可以用一个公式来表达：z = m * x + n * y。
• 其中m，n为舀水和倒水的次数，正数表示往里舀水，负数表示往外倒水，那么题目中的例子可以写成: 4 = (-2) * 3 + 2 * 5，即3升的水罐往外倒了两次水，5升水罐往里舀了两次水。那么问题就变成了对于任意给定的x,y,z，存不存在m和n使得上面的等式成立。根据裴蜀定理，ax + by = d的解为 d = gcd(x, y)，那么我们只要只要z % d == 0，上面的等式就有解，所以问题就迎刃而解了，我们只要看z是不是x和y的最大公约数的倍数就行了，别忘了还有个限制条件x + y >= z，因为x和y不可能称出比它们之和还多的水。（具体实现看代码，beat 100%）

48.（754:Medium）（非常经典题）Reach a Number

• 该题一开始尝试使用BFS搜索求解，但栈溢出，递归搜索的结束条件不容易辨析出来。当从原点一直向左走，而target>0的情况，很难用量化的公式来决定该情况一定不能到达target，不能结束该路径的搜索而跳出循环。
• 其实这道题的正确解法用到了些数学知识，还有一些小trick，首先来说说小trick，第一个trick是到达target和-target（负target）的步数相同，因为数轴是对称的，只要将到达target的每步的距离都取反，就能到达-target。第二个trick很难从字面意思理解，需要用示例来进行演示：从0开始，第一步能够产生{+1, -1}， 第二步能够产生{+1, -1, +3, -3}，我们枚举到第六步，有：

走了0步：0
走了1步：1
走了2步：1 3
走了3步：0 2 4 6
走了4步：0 2 4 6 8 10
走了5步：1 3 5 7 9 11 13 15
走了6步：1 3 5 7 9 11 13 15 17 19 21

• 注意：每一个数字代表的是"绝对值"，也就是说正负都能取到。此外，发现每两行是同奇或同偶的，且该行包含了当前行最大值在内的所有奇数或所有偶数。我们观察最后一列数字，有：

走了0步：0      0 = 0
走了1步：1      1 = 1
走了2步：3      3 = 1 + 2
走了3步：6      6 = 1 + 2 + 3
走了4步：10     10 = 1 + 2 + 3 + 4
走了5步：15     15 = 1 + 2 + 3 + 4 + 5
走了6步：21     21 = 1 + 2 + 3 + 4 + 5 + 6

• 所以首先我们要确定step，最后一个数用sum来表示，如果target > sum说明还没加够，需要继续增加步数，必须让sum >= target，然后才能进行分析。当sum - target为偶数，说明target与sum有相同的奇偶性，target就在此行，直接输出；如果sum - target为奇数，说明sum与target一奇一偶，那么step必须还得往后数，此时，如果step为偶数时 + 1， step为奇数时 + 2（简单来说就是使最终的step的sum值成为与target有相同奇偶性的下一个符合条件的行）

49.（50:Medium）（非常经典题）Pow(x, n)

• 直接使用Java自带的pow函数即可，为了避免越界，需要将n的类型由int强转为double。
• 该题其实考察的是递归或者说是binary search，直接参看如下的代码：

    public double myPow(double x, int n) {
        //DFS
        
        if(x > 1 && n == Integer.MIN_VALUE || x > 0 && x < 1 && n == Integer.MAX_VALUE)
            return 0;
        
        if(n == 0)
            return 1;
        if(n<0){
            n = -n;
            x = 1/x;
        }
        return (n%2 == 0) ? myPow(x*x, n/2) : x*myPow(x*x, n/2);
    }

该题可能本意是希望让我们自己实现幂次运算，下次复习时需要参看学习discuss中的方法

50.（523:Medium）（非常经典题）Continuous Subarray Sum

• 一种非常简单的方法就是暴力求解，尝试所有长度大于等于2的序列和。注意：k=0的情况，和nums数组中所有元素均为0的情况。(暴力解法见代码)
• 该题O(n)的解法是计算累加和，该题和Leetcode 560题解法有点相似，代码如下：

    public boolean checkSubarraySum(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<Integer, Integer>(){{put(0,-1);}};; //初始化时将余数为1的情况考虑进去，索引初始化为-1。key是余数，value是取到该余数的索引下标
        int runningSum = 0; //累加和，但每次和大于k后都要对k取余
        for (int i=0;i<nums.length;i++) {
            runningSum += nums[i];
            if (k != 0) runningSum %= k; //注意是将runningSum对k取余，因为题目要求的是k的倍数
            Integer prev = map.get(runningSum); //查看之前是否有相同的余数，有的话取出之前的index索引
            if (prev != null) {
                if (i - prev > 1) return true;
            }
            else map.put(runningSum, i); //存入余数和取到该余数的索引
        }
        return false;
    }

该题还有更高效的解法，貌似是hashtable，下次复习时参看discuss

51.（166:Medium）（经典题）Fraction to Recurring Decimal

• 该题其实就是模拟两数相除的一个计算过程，我们只需要分别计算整数部分和小数部分，那么就可以将小数的计算转化为整数的计算了。为了判断分数是否为循环小数，我们需要用一个容器来存储之前计算出小数部分的结果（分子）。在test case中，有 1/6 的测试例，结果为 0.1(6)，所以我们还需要记录循环开始的位置，故容器应使用有序的ArrayList而不是Set。因为分数可能为负数，决定结果正负的是整数部分而不是小数部分，所以在计算完整数部分后，应将分子分母均置为正数。
• 在test case中还有测试例为1/-2,147,483,648，int型的取值范围最小值是-2,147,483,648，但最大值是2,147,483,647，绝对值差1。所以为了在将分子分母置为正数的过程中出现上界溢出，应将程序中所有的变量都设为long型。

52.（29:Medium）（非常经典题）Divide Two Integers

• 该题不让使用乘法、除法、模运算，那么唯一可以使用的计算方式就是加法了。一开始尝试每次让dividend减去一个divisor，相当于每次只在上一次结果的基础上值加1，效率很低，超时。后来参看discuss，才知道正确的高效方法是使用bit manipulation的位移操作。
• 其实本质上位移操作就是加法或者乘法运算，每左移一位，值变为原来的2倍，相当于乘2，效率会更高，结果逼近真实值的速度会更快。当然，我们也可以不直接使用位移运算，而使用 result += result的方式间接实现了位移运算的功能，相当于在原来基础上乘了2，这也是为什么该题被分为binary search的原因。同时，我们应注意到，如19/6，我们将6向左位移一次后变为12，那么还需要对剩余的(19-12)/6进行计算，相当于更新被除数的值后递归的进行除法运算，直到被除数小于除数为止。（具体实现细节参看代码实现）

53.（753:Hard）（非常非常经典题）Cracking the Safe

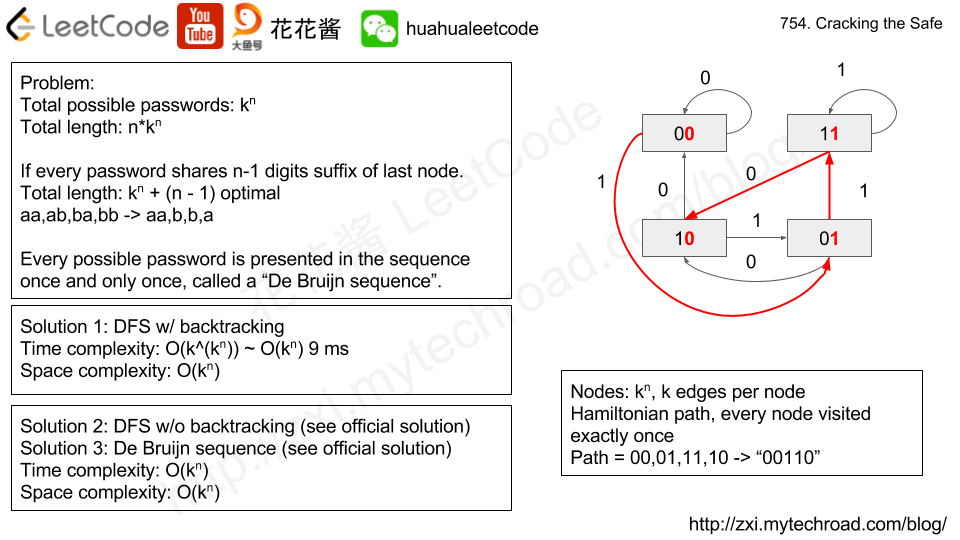
• 该题其实用DFS来解决，该题目本质上相当于是求哈密顿回路问题，即是否存在一个路径能将所有的结点都遍历到且每个结点只遍历一遍，这里的结点就是长度为n的所有password的可能情况。（beat 90%）

• 如上图所示，长度为2的password所有可能情况为00、01、10、11，红色线段连接成一个满足题目条件的路径。我们所求的下一个结点的前n-1个字符是上一个结点的最后n-1个字符，所以对于任意一个结点，都有k条边指向其他k个结点，相当于在当前结点的最后n-1个字符的基础上再拼接一个可能的字符。
• 题目一定存在一个满足上述条件的路径，因为有一个数学定理已经证明了。该题具体的思路请参看代码实现。

参考教学视频：https://www.youtube.com/watch?v=kRdlLahVZDc

该题好像还有利用数学定理来求解的，具体可参看该题的标准答案，下次复习时再研究

54.（517:Hard）（非常经典题）Super Washing Machines

• 个人认为该题并不能算作一个DP问题，因为更新dp[i]时，并没有与dp[0...i-1]建立联系，而是和avgNum一个固定数值进行比较，因为它并没有一个子结构。我们可以把该问题看作一个"管道"，管道大小为1，衣服的移动相当于水流的流动，返回值就是"最大的水位差"。

以一个例子作为说明来窥探规律：
当前machines = [2,2,2]，再加入一个新的machine，内含衣服6件
移动过程如下
     2     2     2 <-- 6
     2     2 <-- 3 <-- 5
     2 <-- 3 <-- 3 <-- 4
     3     3     3     3
那么移动步数为6 - 3 = 3步

• 基于上例的观察，我们需要维护一个move数组，来存储对应位置的machine[i]衣服移动的个数，取最大的move[i]返回即可。具体实现细节及逻辑流程见代码，beat 97%。

55.（483:Hard）（非常经典题）Smallest Good Base

• 该题需要用到一个数学公式的化简，即(x^k - 1)/(x - 1) = n ==> x^k - 1 = n * (x - 1) x是base，k是结果的最高次幂，题目中n = x^(k-1) + x^(k-2) +...+x + 1。根据上式，我们有：当x^k - 1 < n*(x - 1)时，说明base值x太小；反之x^k - 1 > n*(x - 1)时base值x过大。又因为n最大为10^18，而base的最小值为2，所以k的最小值为log2(10^18)=60，即n转换后的结果长度最长为60；而k的最小值为2，因为对于任何的n，n = (n-1) + 1。但我们需要明白，并不是所有的k值都对应着一个base值x；但是，任何n一定存在着某个base值x，最次为x=n-1.
• 基于以上分析，我们便可以从k=60(k越大，则x越小)开始搜寻x，设立left、right指针初始化为left=2、right=n-1，然后二分搜索mid值，求出当前k的对应base值x；若不存在，则将k--，计算下一个长度的x值。（个人感觉像暴力求解）
• 注意：二分查找中，循环条件l <= h，则循环中包含了l=h值时的运算，但循环条件若为l<h，则l=h值的运算需要在循环外单独处理

具体实现细节见代码，上面的分析给出了该题目的解决思路，但代码提交只beat 14%，可能某些数据结构还可以优化

56.（780:Hard）（非常经典题）Reaching Points

• 一开始想到直接使用DFS求解，但奈何加法运算效率太低，Stack Overflow，所以只能结合特征考虑将该思路进行简化。
• 我们观察式子(x, y) -> (x + y, y) or (x, x + y)，如果两者交替相加，那递归深度大是必然的，但很多情况下可以这么transform：

(x, y) -> (x + y, y) -> (x + 2y, y) -> (x + 3y, y)

那么当存在tx很大的情况时，我们可以发现tx直接余上ty就能直接省去若干的叠加。那么递归深度也以指数级减少。

比如 (x + 3y) % y = x, 所以只需要一步从(x + 3y, y) -> (x, y)

• 那么当我们在某一层得到tx、ty时，当tx > ty, tx = tx % ty，因为reach (tx,ty)时，最后一步一定是tx = tx + ty；类似的，当tx < ty， ty = ty % tx，因为reach (tx,ty)时，最后一步一定是ty = tx + ty。我们可以想象为，这是一种借助取余的逆回溯方法。

<57>.（233:Hard）（没搞懂）Number of Digit One

• 该题应使用数学归纳法进行求解，用暴力解法应超时。下面是不同范围内1的个数规律统计：

1的个数        含1的数字                                                      数字范围

1             1                                                            [1, 9]

11            10  11  12  13  14  15  16  17  18  19                       [10, 19]

1             21                                                           [20, 29]

1             31                                                           [30, 39]

1             41                                                           [40, 49]

1             51                                                           [50, 59]

1             61                                                           [60, 69]

1             71                                                           [70, 79]

1             81                                                           [80, 89]

1             91                                                           [90, 99]

11            100  101  102  103  104  105  106  107  108  109             [100, 109]

21            110  111  112  113  114  115  116  117  118  119             [110, 119]

11            120  121  122  123  124  125  126  127  128  129             [120, 129]

...           ...                                                          ...

参考链接：中文博客  discuss高票答案

参考视频：中文讲解视频

该题没有搞懂，下次复习时应与其他同学讨论学习

58.（224:Hard）（非常非常经典题）Basic Calculator

• 因为该题中，操作符只有正号、负号，所以可以不用逆波兰表达式，只借助一个堆栈即可解决该问题。但个人认为，若加减乘除均包含的话，应该将中序表达式转化为逆波兰表达式，然后再计算为好。
• 该题核心思路是：用一个变量sign记录下一个数字或等式的正负号。对于括号的处理，我们先将括号外层的已计算结果及括号内等式的正负号压栈，待括号内结果已经计算完毕，我们再返回上一层，将括号内结果与括号外结果进行合并即可。具体的实现细节参看代码实现。
• 对于更一般等式的计算，应该先将中序表达式转化为逆波兰表达式，因为逆波兰表达式的操作符是按优先级排列的，所以去掉了括号的干扰。转换及计算策略如下：

后缀表达式在四则运算中带来了意想不到的方便，在生成过程中自动保持了优先级；

生成逆波兰表达式的算法如下：

我们首先的用两个栈结构来存储运算符和操作数，在java中有Stack类可以用；

从左到右遍历我们输入的中缀表达式：

1、如果是操作数的话，那么就直接压入存放操作数的堆栈；

2、如果是"("左括号的话，那么就直接压入存放运算符的堆栈；

3、如果是")"右括号的话，那么就从运算符堆栈中弹数据，并将弹出的数据压入到操作数堆栈中，直到遇到"("为止，这里值得注意的是，"("是必须要从运算符堆栈中弹出的，但是不压入到操作数堆栈，后缀表达式中是不包含括号的；

4、如果是其他符号，就是其他的运算符+-*/这些，那么就：

a、如果运算符堆栈为空，则直接压入运算符堆栈；

b、如果不为空且此时运算符堆栈的栈顶元素为括号，包括左括号和右括号，那么也是直接压入运算符堆栈中；

c、如果此时遍历到的元素的优先级比此时运算符堆栈栈顶元素的优先级高，则直接压入运算符堆栈；

d、如果正在遍历的元素的优先级和运算符堆栈栈顶的元素的优先级相等或者更小，则需要将栈顶元素弹出并且放到操作数堆栈中，并且将正在遍历的元素压入到运算符堆栈，其实运算符堆栈中的元素顺序就是优先级的顺序；

5、直到遍历完表达式，此时还需要将运算符堆栈中的所有元素压入到操作数堆栈中，算法完成。

根据以上算法可以得到逆波兰表达式，我们得到逆波兰表达式之后，必须求得正确的计算结果，有了逆波兰表达式，计算起来就攘夷多了，算法如下：

用另一个堆栈来保存数据，从左到右遍历逆波兰表达式：

1、如果是数字，则直接压入堆栈中；

2、如果是运算符（+,-,*,/），则弹出堆栈中的两个数据，进行相应的计算，计算完成之后得到一个数据，然后又压入堆栈中；

3、直到遍历完成，此时堆栈中的数据就是最后计算的结果

参考教程：中文视频讲解

59.（149:Hard）（非常经典题）Max Points on a Line

• 该题“只能”通过暴力解法brute force进行解决，没有什么诀窍，最多就是使用了HashMap存储直线斜率和对应斜率的直线上的点个数。此外，需要注意垂直于x轴的直线(斜率无穷大)、相同点、以及斜率存储的问题，为了避免精度误差，这里斜率k使用“约分后的分数字符串”进行保存。
• 但个人认为，如果只比较斜率，而不考虑y=ax+b中的常数项b，是不正确的，可能测试例test case并没有针对该点进行测试，下次复习时应与其他同学进行讨论。
• 具体实现细节参看代码，参考视频教程：中文视频讲解

60.（335:Hard）（经典题/烂题？）Self Crossing

• 该题没有任何算法知识，只需要分成三种情况，进行边长之间的讨论即可：

 情况1：                         情况3：
	             b                            b							
	   +----------------+             +----------------+
	   |                |             |                |
	   |                |             |                | a
	 c |                |           c |                |
	   |                | a           |                |    f
	   +----------->    |             |                | <----+
	            d       |             |                |      | e
	                    |             |                       |
	                                  +-----------------------+
	                                               d
 情况2：                                      
	             b                          
	   +----------------+            
	   |                |           
	   |                |          
	 c |                |         
	   |                | a          
	   +----------->o---|    两条线重合        
	            d                     

• 具体判别条件请参看代码，参考视频：中文讲解视频

61.（412:Easy）Fizz Buzz

• 简单题，i从1到n，判断i是否能整除3或5即可。

62.（973:Easy）K Closest Points to Origin

• 个人认为该题是一个典型的使用Priority Queue的问题

63.（836:Easy）（非常非常经典题）Rectangle Overlap

• 首先，返璞归真，在玩2D之前，先看下1D上是如何运作的。对于两条线段，它们相交的话可以是如下情况：

           x3             x4
           |--------------|
 |--------------|
 x1             x2

• 我们可以直观的看出一些关系： x1 < x3 < x2 && x3 < x2 < x4。可以稍微化简一下：x1 < x4 && x3 < x2
• 就算是调换个位置：

           x1             x2
           |--------------|
 |--------------|
 x3             x4

• 还是能得到同样的关系：x3 < x2 && x1 < x4
• 注意到，x3 < x2和x1 < x4其实是选取的参照物不同而需要满足的两种不同情况。例如两个线段l1和l2，一个是l1在前的参照，一个是l2在前的参照。
• 好，下面我们进军2D的世界，实际上2D的重叠就是两个方向都同时满足1D的重叠条件即可。由于题目中说明了两个矩形的重合面积为正才算overlap，就是说挨着边的不算重叠，那么两个矩形重叠主要有这四种情况：

1. 两个矩形在矩形1的右上角重叠：满足的条件为x1 < x4 && x3 < x2 && y1 < y4 && y3 < y2

           ____________________x4,y4
          |                   |
   _______|______x2,y2        |
  |       |______|____________|
  |      x3,y3   |
  |______________|
 x1,y1

2. 两个矩形在矩形1的左上角重叠：满足的条件为x3 < x2 && x1 < x4 && y1 < y4 && y3 < y2

   ___________________  x4,y4
  |                   |
  |            _______|____________x2,y2
  |___________|_______|           |
x3,y3         |                   | 
              |___________________|
            x1,y1

3. 两个矩形在矩形1的左下角重叠：满足的条件为x3 < x2 && x1 < x4 && y3 < y2 && y4 < y1

           ____________________x2,y2
          |                   |
   _______|______x4,y4        |
  |       |______|____________|
  |      x1,y1   |
  |______________|
 x3,y3

4. 两个矩形在矩形1的右下角重叠：满足的条件为x1 < x4 && x3 < x2 && y3 < y2 && y4 < y1

   ___________________  x2,y2
  |                   |
  |            _______|____________x4,y4
  |___________|_______|           |
x1,y1         |                   | 
              |___________________|
            x3,y3

• 仔细观察可以发现，上面四种情况的满足条件其实都是相同的，只不过顺序调换了位置，所以我们只要一行就可以解决问题了

64.（794:Easy）（非常经典题）Valid Tic-Tac-Toe State

• When turns is 1, X moved. When turns is 0, O moved. rows stores the number of X or O in each row. cols stores the number of X or O in each column. diag stores the number of X or O in diagonal. antidiag stores the number of X or O in antidiagonal. When any of the value gets to 3, it means X wins. When any of the value gets to -3, it means O wins.
• When X wins, O cannot move anymore, so turns must be 1. When O wins, X cannot move anymore, so turns must be 0. Finally, when we return, turns must be either 0 or 1, and X and O cannot win at same time. 在代码实现时，紧紧扣住这些条件进行判断即可。

65.（885:Medium）（非常经典题）Spiral Matrix III

• 根据example 2，我们可以发现当向右走或者向左走的时候，遍历的len总是在原来基础上加1，于是根据行走的步长，有序列:1,1,2,2,3,3,4,4...。所以，我们沿着当前方向行走len步，在行走过程中，若当前位置的元素不在grid上，我们不将其加入res结果集中，只增加当前已行走的步长i，当在该方向走完len步后，换方向，方向依次为east->south->west->north。参考代码如下：

public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {
	int[][] res = new int[R*C][2];
	int[][] dir = new int[][] {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // east, south, west, north
	int len = 0, d = 0; // move <len> steps in the <d> direction
	res[0] = new int[] {r0, c0};
	int size = 1;
	while(size < R*C) {
	  if (d == 0 || d == 2) len++; // when move east or west, the length of path need plus 1，根据图片观察出的规律
             for (int i = 0; i < len; i++) {
                r0 += dir[d][0];
                c0 += dir[d][1];
                if (r0 >= 0 && r0 < R && c0 >= 0 && c0 < C) { // check valid，如果在grid中才加入res中
                    res[size] = new int[] {r0, c0};
                    size++;
                }
             }
            d = (d + 1) % 4; // turn to next direction，遍历完这个方向的长度后，换方向
        }
		
	return res;
}

66.（829:Medium）（非常非常经典题）Consecutive Numbers Sum

• 这道题的要求的另一种说法: 把N表示成一个等差数列（公差为1）的和，我们不妨设这个数列的首项是x，项数为m，则这个数列的和就是[x + (x + (m-1))]m / 2 = mx + m(m-1)/2 = N。
• 接下来，一个很自然的想法就是，枚举m，通过上式判断对于相应的m是否存在合法的x。x = ((N - m(m-1)/2)) / m.显然枚举的复杂度是O(sqrt(N))。因为m能取到的最大值显然是sqrt(n)数量级的
• O(N)时间复杂度的解法超时，所以只能选取O(sqrt(n))数量级的解法

67.（942:Easy）（经典题）DI String Match

• Outside-in思想

public int[] diStringMatch(String S) {
    int n = S.length(), left = 0, right = n;
    int[] res = new int[n + 1];
    for (int i = 0; i < n; ++i)
        res[i] = S.charAt(i) == 'I' ? left++ : right--;
    res[n] = left;
    return res;
}

68.（963:Medium）（非常经典题）Minimum Area Rectangle II

• 要解决该问题，首先一个intuition是：矩形的两条斜边有相同的长度，且两条边的中点相同，基于此我们有如下的设计：

1. Two diagonals of a rectangle bisect each other, and are of equal length.
2. The map's key is String including diagonal length and coordinate of the diagonal center; map's value is the index of two points forming the diagonal.

public double minAreaFreeRect(int[][] points) {
    int len = points.length;
    double res = Double.MAX_VALUE;
    if (len < 4) return 0.0;
    Map<String, List<int[]>> map = new HashMap<>(); // int[] is the index of two points forming the diagonal
    for (int i = 0; i < len; i++) {
        for (int j = i + 1; j < len; j++) {
            //可以看成计算矩形斜边的长度：x^2+y^2
            long dis = (points[i][0] - points[j][0]) * (points[i][0] - points[j][0]) + (points[i][1] - points[j][1]) * (points[i][1] - points[j][1]);
            //矩形斜边的中点
            double centerX = (double)(points[j][0] + points[i][0])/2; // centerX and centerY is the coordinate of the diagonal center
            double centerY = (double)(points[j][1] + points[i][1])/2;
            //当两条边有相同长度，切中点相同时，这两条边对应的四个顶点一定可以组成一个矩形
            String key = "" + dis + "+" + centerX + "+" + centerY; // key includes the length of the diagonal and the coordinate of the diagonal center
            if (map.get(key) == null) map.put(key, new ArrayList<int[]>());
            //具有相同长度，相同中点的斜边可能有很多个，将斜边的端点索引记录下来
            map.get(key).add(new int[]{i,j});
        }
    }
    for (String key : map.keySet()) {
        if (map.get(key).size() > 1) {
            List<int[]> list = map.get(key);
            for (int i = 0; i < list.size(); i++) { // there could be multiple rectangles inside
                for (int j = i + 1; j < list.size(); j++) {
                    //找到一个斜边的两个端点和另外一个斜边的一个端点
                    int p1 = list.get(i)[0]; // p1, p2 and p3 are the three vertices of a rectangle
                    int p2 = list.get(j)[0];
                    int p3 = list.get(j)[1];
                    // len1 and len2 are the length of the sides of a rectangle，计算由这两条斜边组成的矩形的长和宽
                    double len1 = Math.sqrt((points[p1][0] - points[p2][0]) * (points[p1][0] - points[p2][0]) +  (points[p1][1] - points[p2][1]) * (points[p1][1] - points[p2][1]));
                    double len2 = Math.sqrt((points[p1][0] - points[p3][0]) * (points[p1][0] - points[p3][0]) +  (points[p1][1] - points[p3][1]) * (points[p1][1] - points[p3][1]));
                    double area = len1 * len2;
                    res = Math.min(res, area);
                }
            }
        }
    }
    return res == Double.MAX_VALUE ?  0.0 : res;
}