Heap (Java) - ShuweiLeung/Thinking GitHub Wiki

该页笔记始于"2018.6.6"，结于“2018.6.10”，使用Java语言

对于数组长度上千的问题规模，算法时间复杂度在O(n^2)的算法是一定会超时的，只能为O(n)或O(nlogn)。

1.（378:Medium）（非常经典题）Kth Smallest Element in a Sorted Matrix

Heap其实就是借助PriorityQueue来实现的，此外，为了保证我们便于判断当前元素是否应该插入堆中，我们需要自定义一个比较器，将heap变为一个最大堆，于是堆顶元素就是最大的元素，当当前的堆中元素个数达到k时，只有比堆顶元素小的值才被插入，同时删除堆顶元素。（beat 46%）
二分搜索的方法：

    public int kthSmallest(int[][] matrix, int k) {
        int lo = matrix[0][0], hi = matrix[matrix.length - 1][matrix[0].length - 1] + 1;//[lo, hi)
        while(lo < hi) {
            int mid = lo + (hi - lo) / 2;
            int count = 0,  j = matrix[0].length - 1;  //count是当前比mid小的总元素个数
            for(int i = 0; i < matrix.length; i++) {
                while(j >= 0 && matrix[i][j] > mid) j--;  //统计每行比mid小的个数
                count += (j + 1);
            }
            if(count < k) lo = mid + 1;
            else hi = mid;  //关键：即使count=k，hi依然更新为node，而不是直接返回mid，因为matrix中可能没有元素值等于mid
        }
        return lo;
    }

上面的思路并有使用到题目中给出的每行及每列元素均升序的性质，下次复习时应参看discuss中更高效答案

2.（215:Medium）（非常非常经典题）Kth Largest Element in an Array

该题思路和上面第1题（378）相同，只不过建立一个最小堆即可，当堆的大小等于k后，只有比堆顶大的元素才加入堆，同时删去原来堆顶的元素。（beat 72%）
该题可以利用快排的partition思想，最后返回哨兵排序后的位置来解决该问题，该题代码及快速排序的partition算法如下：

    public int findKthLargest(int[] nums, int k) {
        int left = 0, right = nums.length - 1;
        int targetPosition = nums.length - k;  //若将nums升序排列，则返回的元素位置应该是targetPosition
        while(true){
            int pos = quickSort(nums, left, right);
            //类似于二分搜索
            if(pos == targetPosition)
                return nums[pos];
            else if(pos > targetPosition)
                right = pos - 1;
            else
                left = pos + 1;
        }
    }
    
    //快速排序的partition算法
    public int quickSort(int[] a,int low,int high){
        int p = a[low];  //哨兵
        int i = low + 1;  // i指向的是比哨兵p大的元素，i左侧的元素都比哨兵小，i右侧的元素都比哨兵大于或等于
        
        for(int j = low + 1; j <= high; j++) {  //j是一个不断向前扫描的指针
        		if(a[j] < p) {  //比哨兵小的元素都放在i的左边
        			swap(a, j, i);
        			i++;
        		}
        }
        
        swap(a, low, i - 1); //i比哨兵大于或等于，i-1是恰好小于哨兵的元素
        return i-1;
     }
    
    public void swap(int[] nums, int left, int right){
        int t = nums[left];
        nums[left] = nums[right];
        nums[right] = t;
    }

该题的时间复杂度为O(n)，不是O(nlogn)，解释如下链接，简单来说，quick sort会进行logn次二分，对于每次二分，都会遍历整个数组序列n，所以时间复杂度为O(nlogn)，而quick select也会进行logn次二分没错，但每次二分都只会遍历那次二分长度的一个片段，即O(n)+O(n/2)+O(n/4)+O(n/8)+... <= O(2n)（具体可以参看ipad上画的一个比较形象的图示）：

The average case for quick select is O(n) while the worst case is O(n2). Below are links to some explanations I found out:

Stackoverlow on why it is O(n)

http://stackoverflow.com/questions/8783408/why-is-the-runtime-of-the-selection-algorithm-on

http://stackoverflow.com/questions/5945193/average-runtime-of-quickselect

Wikipedia:

https://en.wikipedia.org/wiki/Selection_algorithm

该题当然还有其他方法，如divide and conquer，下次复习时可以再参考

3.（659:Medium）（非常非常经典题）Split Array into Consecutive Subsequences

该题首先用一个freq统计每个数字的出现次数，然后用appendfreq来存储"之前序列之后待追加的数字"。例如，对于序列[2,3,4]，它的待追加序列为5，且因为该序列只有一个，所以只能有一个5能追加到之前已经产生的序列后。对于数字i，我们首先判断其是否能追加到之前的序列末尾，若不能，则判断是否存在i+1、i+2组成长度为3的consecutive sequence，若存在，则将三个数字的频率减1，并将i+3作为待追加数字；否则，返回false。
该题感觉有一定难度，思路需要整理清楚才能求解。

该题还有其他思路，下次复习时可以学习

<4>.（743:Medium）（难题）（非常经典题）Network Delay Time

该题使用 Djikstra's 算法，它是一个有向图，具体思路参考代码。

It is a direct graph.

Use Map<Integer, Map<Integer, Integer>> to store the source node, target node and the distance between them.
Offer the node K to a PriorityQueue.
Then keep getting the closest nodes to the current node and calculate the distance from the source (K) to this node (absolute distance). Use a Map to store the shortest absolute distance of each node.
Return the node with the largest absolute distance.

该题大方向使用Djikstra's 算法，实现细节比较复杂，下次复习时还需要再看再研究

5.（373:Medium）Find K Pairs with Smallest Sums

该题我是用的最直接的方法，直接用一个PriorityQueue，建立一个比较器，让二元数组和最小的排在堆顶（最小堆），然后将所有排列组合情况都加入到优先队列中，最后取前k个返回。（beat 17%）
高效的思路：一开始存(nums1[0], nums2[0]), (nums1[1], nums2[0]), (nums1[2], nums2[0]), ... (nums1[n], nums2[0])，从中取出最小的pair例如(nums1[m], nums2[0])之后，我们放入(nums1[m], nums2[1]),按这样取k次，每次的复杂度为O(logk)，所以总的时间复杂度为O(klogk)。过程如下图所示

    public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        PriorityQueue<int[]> que = new PriorityQueue<>((a,b)->a[0]+a[1]-b[0]-b[1]);
        List<int[]> res = new ArrayList<>();
        if(nums1.length==0 || nums2.length==0 || k==0) return res;
        for(int i=0; i<nums1.length && i<k; i++) que.offer(new int[]{nums1[i], nums2[0], 0});
        while(k-- > 0 && !que.isEmpty()){
            int[] cur = que.poll();
            res.add(new int[]{cur[0], cur[1]});
            if(cur[2] == nums2.length-1) continue;
            que.offer(new int[]{cur[0],nums2[cur[2]+1], cur[2]+1});
        }
        return res;
    }
    
    /*
    * 下面的方法时间复杂度比较高，因为我们只需要存前k个pairs到pq里即可
    public List<int[]> kSmallestPairs(int[] nums1, int[] nums2, int k) {
		PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> {return (a[0]+a[1]) - (b[0]+b[1]);});
		//Queue<int[]> q = new LinkedList<>();
		for(int i = 0; i < nums1.length; i++) {
			for(int j = 0; j < nums2.length; j++) {
				int[] pair = {nums1[i], nums2[j]};
				pq.add(pair);
			}
		}
		
		List<int[]> res = new ArrayList<>();
		while(!pq.isEmpty() && res.size() < k) {
			res.add(pq.poll());
		}
		
		return res;
	}
    */

<6>.（787:Medium）Cheapest Flights Within K Stops

该题同样是一道graph题目，和第4题（743）类似，我们用 Dijkstra's algorithm算法求最短路径，同时维护一个可继续前进的步数，该步数必须大于等于0，否则返回-1。具体思路请参看代码实现及注释。

<7>.???（778:Hard）（该题不会做）Swim in Rising Water

该题不会做，下次复习时与其他同学请教

<8>.（407:Hard）（非常非常经典题）Trapping Rain Water II

该题是Leetcode Array类题目中的第42题的扩展，该题直接参看Discuss。思路为：我们要想存水，就要有一个边界，就像一个盒子一样，只有盒子里面才能装东西。因此，我们先将矩阵的边界作为这个盒子。但是，我们要意识到，储水的过程类似于木桶原理，边界线上最小的高度才是整个盒子真正的高。因此我们用一个最小堆PriorityQueue来存储边界线上的高度，然后每次都取最小的高度，然后与其相邻未访问过的grid进行高度比较，如果相邻grid的高度较低，那么当前最小堆的堆顶元素高度与该相邻grid的高度差就是该grid的储水量。原因是，边界线上没有其他高度比当前堆顶元素的高度还低。之后，因为弹出了堆顶，我们需要更新边界值，那么该相邻grid的高度我们取它的真实高度和原堆顶元素高度的较大值，这样可以保留之前的信息，才能算出正确的储水量。直到grid数组中所有位置都被访问过，才返回。具体思路可以参看代码及注释。

9.（502:Hard）（非常经典题）IPO

该题其实有点像之前做过的一道题，首先我们要明确：capital大的project不一定要比capital小的project获益多。所以，我们不能到达一个资金水平后，就将能做的项目都做了从而消耗掉k。
正确的思路是：用一个最小堆pq来存储开始的所有项目，资金要求越小的项目排的位置越靠前。当我们能够做一些项目时，就将这些可做的项目按收益大小放到一个最大堆preCapitalProjects（收益越大越靠前）中；当下一次从剩余的projects中（pq中存储的剩余项目）选择最小的收益标准的项目P，若当前公司没达到该Capital标准，则从可做项目中（preCapitalProjects的项目）选取能获得最大收益的几个项目来积累资本，直到当前资本达到P的最小收益标准后停止，然后再将该Capital级别的项目（和P的资本要求相同的项目）放入最大堆中，继续上述循环。直到pq中没有项目，说明当前的资本可以做任何项目，那么我们从preCapitalProjects中做前curK个项目即可，最后返回curCapital。
注意：有的时候k的值比项目的总数还多。

该题思路必须理的非常清晰也是自己独立完成的，建议下次复习时也要好好看一下该题，也可以参考一下discuss中其他方法

<10>.（239:Hard）Sliding Window Maximum

用大顶堆存储k个元素，每次窗口后移一个单位，去掉nums[i-1]，向堆中加入nums[i+k-1]，取堆顶元素放在当前的返回数组位置上即可。（beat 2%）

该题还有其他更高效的方法，下次复习时参考discuss

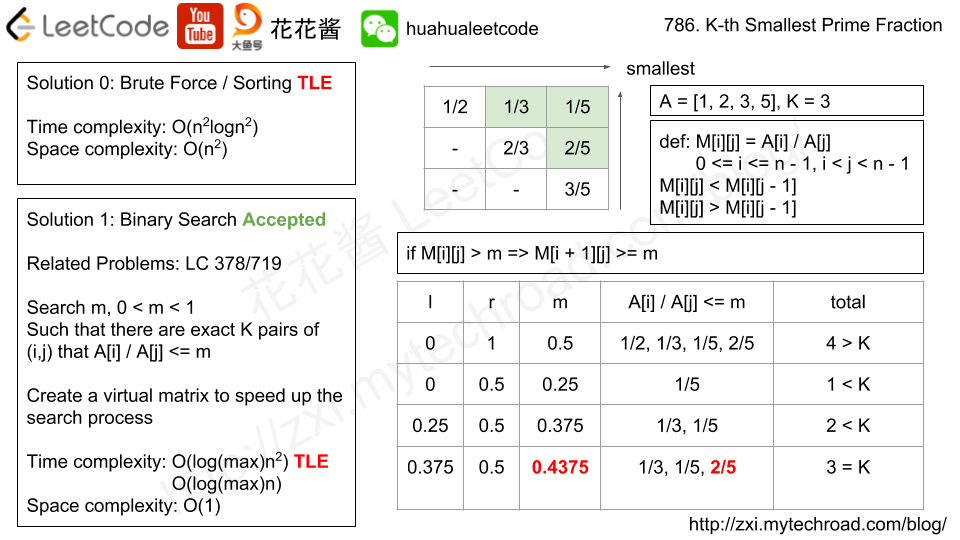
11.（786:Hard）（非常经典题）K-th Smallest Prime Fraction

参考链接：Summary of solutions for problems "reducible" to LeetCode 378。Discuss中关于第k小问题的总结
对于数组长度上千的问题规模，算法时间复杂度在O(n^2)的算法是一定会超时的，只能为O(n)或O(nlogn)。
这里参考花花的二分搜索思路，该思路同样适用于Leetcode 378/719题，同样的思路。二分搜索并不是直接找到第K个分数，而是设立一个上限m，当小于m的分数为k个时，我们寻找到k个分数中的最大值即为答案；否则调整二分搜索的low和high，使小于m的分数个数为合适值。

我们参考图片右上角的矩阵，我们在实现时并不是将其构造出来，而是虚拟的用两个i指针i、j来模拟。矩阵中的元素M[i][j]=A[i]/A[j]。且对于某个位置M[i][j]，M[i][j] < M[i][j-1]（即左面的分数比右边的分数大），M[i][j] > M[i-1][j]（即上面的分数比下面的分数小）。右下角的表格是二分搜索的一个过程。那么当low和high固定后，我们扫描每一行寻找比当前m小的分数个数，当扫描到某个位置A[i]/A[j]>m时，则该行不用再往后扫描，根据上面的性质，当前的i、j代表的分数是当前小于m的分数中最大的。具体实现思路可以参看代码及参考链接视频。
参考链接：花花中文视频讲解

上面的思路是二分搜索（beat 92%），下次复习时可以参看其他discuss中的思路

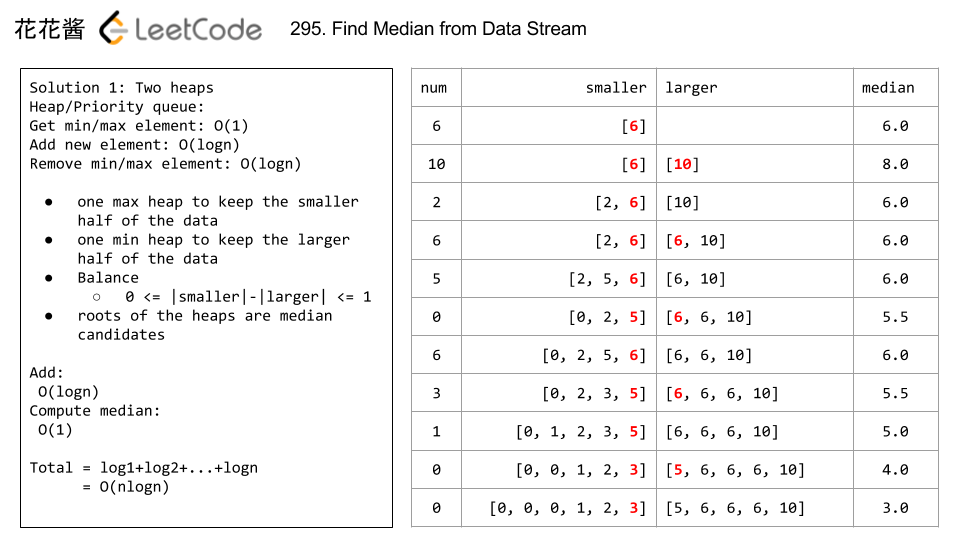
12.（295:Hard）（非常非常经典题）Find Median from Data Stream

该题一种方法是使用Heap，设立两个Heap，一个最大堆less，一个最小堆bigger，当添加的num比less的堆顶元素小或相等时加入到less堆，否则加入到bigger堆。此外要保证两个堆的元素数量不超过1，这样确保中位数只需要从两个堆的堆顶元素获取即可。具体可以参看下图示例和参考链接。

参考链接：花花讲解视频，Heap和Binary Search两种方法

该题还有二分法的解法，下次复习时再参考花花的讲解视频学习

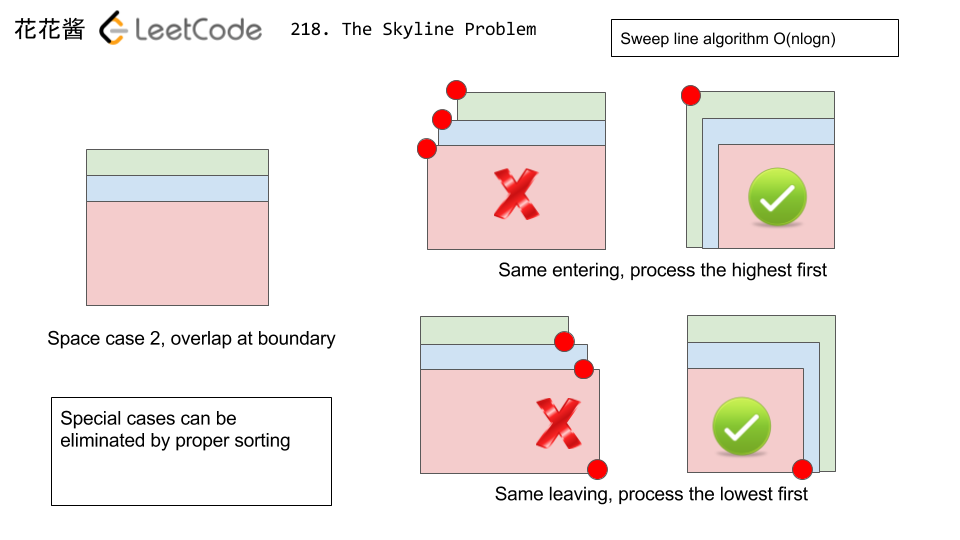
<13>.（218:Hard）（非常非常经典题）（面试题）The Skyline Problem

"扫描线算法"是几何题中经常会用到的一个方法。该题是面试中经常被问到的题目，且本身难度也较大。
该题的思路是：用扫描线算法从左往右扫描每一个渐入点和离开点的横坐标及对应高度，并按x坐标位置从左到右排序。这里使用了一个小技巧，对于渐入点，我们将其高度设为"相反数(负数)"，而离开点的高度仍为原来的"正数"。这样在相同的x坐标的情况下，对于渐入点，会先处理高度较高的点，对于离开点，会先处理高度较低的点，从而不会发生天际线扫描的错误。当buildings的位置重叠只是高度不同时，这两种特殊情况可由上述办法解决，具体请参看下图图示：

该题对于每一个"渐入点"，将当前"最大"高度和渐入点的x轴坐标存入结果集中;对于每一个"离开点"，将当前"次大"高度和离开点的x轴坐标存入结果集中。为了解决当离开点的次大高度为0的情况，我们初始时将0加入到优先队列中。该题的具体思路请参看代码及详细代码注释，和参考链接视频。通过观察示例图，只会用到最高的大楼和次高的大楼两个高度。
参考链接：花花讲解视频 Edward Shi讲解(只有一半讲解)

14.（818:Hard）Race Car

非常难的题目，参考视频教程：花花两种方法讲解

该题可以用DP或Binary Search来求解，因为题目较难，讲解视频时间较长，第一次做时没看，下次复习时参考花花视频学习研究

15.（703:Easy）Kth Largest Element in a Stream

用PriorityQueue即可，看下面的代码：

class KthLargest {
    final PriorityQueue<Integer> q;
    final int k;

    public KthLargest(int k, int[] a) {
        this.k = k;
        q = new PriorityQueue<>(k);
        for (int n : a)
            add(n);
    }

    public int add(int n) {
        if (q.size() < k)
            q.offer(n);
        else if (q.peek() < n) {
            q.poll();
            q.offer(n);
        }
        return q.peek();
    }
}

16.（857:Hard）（非常非常经典题）Minimum Cost to Hire K Workers

首先需要解读题目里给的条件：

Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.意味着，我们最后付的工资是按当前group里面worker期望的最大ratio来给的，每个worker的期望ratio是wage[i] : quality[i]。
Every worker in the paid group must be paid at least their minimum wage expectation.该条件说明，最终的cost = 选中的works中最大的ratio * 总共的weight。

基于上面的分析，为了取得最小的cost，一个是使最大的ratio尽量小，一个是使整体的weight尽量小。我们需要首先按照每个worker的ratio进行排序，先选取k个ratio最小的workers，然后之后在挑选新worker的时候，ratio一定大，但为了使整体的cost最小，我们应该移除现有group中weight最大的人。前者根据ratio排序可以用arraylist实现，后者移除最大的weight可以用pq(heap)来实现。

//需要明确一点：最终的cost = 选中的works中最大的ratio * 总共的weight
public double mincostToHireWorkers(int[] quality, int[] wage, int K) {
    double[][] workers = new double[quality.length][2];
    for (int i = 0; i < quality.length; ++i)
        //第一个元素是期望的最低ratio，第二个元素是quality
        workers[i] = new double[]{(double)(wage[i]) / quality[i], (double)quality[i]};
    Arrays.sort(workers, (a, b) -> Double.compare(a[0], b[0])); //根据ratio从小到大排序
    double res = Double.MAX_VALUE, qualitySum = 0;
    PriorityQueue<Double> pq = new PriorityQueue<>(); //堆顶是最小的weight
    for (double[] worker: workers) {
        qualitySum += worker[1]; //先选择的是当前最小ratio worker
        pq.add(-worker[1]); //实际上相当于是按weight从大到小排序，因为存入的是相反数
        if (pq.size() > K) qualitySum += pq.poll(); //因为pq中存的是负数，所以优先取最负的数，即最大的负数，这里加法等于正数的减法，减去最大的质量
        if (pq.size() == K) res = Math.min(res, qualitySum * worker[0]); //乘的是当前访问的worker的ratio，因为该ratio一定是目前为止最大的
    }
    return res;
}

参考链接：discussion讲解视频讲解

Heap (Java) - ShuweiLeung/Thinking GitHub Wiki

该页笔记始于"2018.6.6"，结于“2018.6.10”，使用Java语言

对于数组长度上千的问题规模，算法时间复杂度在O(n^2)的算法是一定会超时的，只能为O(n)或O(nlogn)。

⚠️ **GitHub.com Fallback** ⚠️

⚠️ GitHub.com Fallback ⚠️