Dynamic Programming (Java) - ShuweiLeung/Thinking GitHub Wiki

该页笔记始于"2018.6.22"，结于“2018.7.16”，使用Java语言

What is DP?

Divide-and-conquer algorithms partition the problem into disjoint subproblems, solve the subproblems recursively, and then combine their solutions to solve the original problem. In contrast, dynamic programming applies when the subproblems overlap—that is, when subproblems share subsubproblems.In this context, a divide-and-conquer algorithm does more work than necessary, repeatedly solving the common subsubproblems. A dynamic-programming algorithm solves each subsubproblem just once and then saves its answer in a table, thereby avoiding the work of recomputing the answer every time it solves each subsubproblem.

We typically apply dynamic programming to optimization problems. Such problems can have many possible solutions. Each solution has a value, and we wish to find a solution with the optimal (minimum or maximum) value. We call such a solution an optimal solution to the problem, as opposed to the optimal solution, since there may be several solutions that achieve the optimal value.

The difference between DP and Greedy

In particular, problems to which greedy algorithms apply have optimal substructure. One major difference between greedy algorithms and dynamic programming is that instead of first finding optimal solutions to subproblems and then making an informed choice, greedy algorithms first make a “greedy” choice—the choice that looks best at the time—and then solve a resulting subproblem, without bothering to solve all possible related smaller subproblems.

The difference between DP and Divide-and-Conquer

A problem for which a divide-and-conquer approach is suitable usually generates brand-new problems at each step of the recursion. Dynamic-programming algorithms typically take advantage of overlapping subproblems by solving each subproblem once and then storing the solution in a table where it can be looked up when needed, using constant time per lookup.

DP问题求解步骤（白话文表示，更精确的表述请参考《算法导论》）

找出最优子结构，用自然语言描述出来
根据自然语言表示出数值之间的等式关系（递推式）
根据数值之间的等式关系自底向上或从上到下编写程序
在程序实现过程中，记录最优的答案（可选）

1.（70:Easy）（经典题）Climbing Stairs

该题与之前Dynamic Programming类第746题Min Cost Climbing Stairs思路很相似。该题要求我们找出到达第n个阶梯的所有走法数量，我们可以想到，ways[n] = ways[n-1] + ways[n-2]，即到达第n个阶梯可以从第n-1个阶梯走一步或n-2个阶梯走两步到达，这便得到了最优子结构及递推关系式，初始变量为ways[0] = ways[1] = 1。

2.（198:Easy）（非常非常经典题）House Robber

该题有两种解法，思路一样，只是一个化简一个没化简，可参考如下：
我们设立两个数组yes和no分别代表抢第i个房子和不抢第i个房子，那么最优子结构就是：我们如果要抢第i个房子，则第i-1个房子肯定不能抢，那么yes[i]的值就应该是"抢或不抢第i-2个房子的最大值+第i个房子的价值"；如果不抢第i个房子，则小偷经过第i个房子所能获得的最大价值no[i]是抢或不抢第i-1个房子的最大价值。这样便可得到递推式：yes[i] = Math.max(yes[i-2] + nums[i], no[i-2] + nums[i])和no[i] = Math.max(yes[i-1], no[i-1])。最终返回的是偷第n个房子或者不偷第n个房子的最大值。（beat 2%）
上面的思路其实可以进行化简，我们会发现，如果只设立一个rob数组来存储偷到第i个房子的最大价值，那么rob[i] = max(rob[i-2]+money[i],rob[i-1])，从而将空间复杂度从O(n)降为O(1)。

3.（303:Easy）Range Sum Query - Immutable

该题运用的主要技巧就是：第i个数到第j个数的和 = 前j个数的和 - 前i-1个数的和

4.（338:Medium）（非常经典题）Counting Bits

该题一开始发现，相邻两数相差1，所以i的二进制表示是在i-1的二进制表示基础上加1，但是，这个规律对我们统计1的个数并没有帮助，因为我们并没有利用到之前已经得出的结果，且按上述规律还需要计算出每个数字的二进制表示才能得出答案。
正确的做法是（自己想的），对于数字6，我们可以将其减去2^2，得2，因为我们已经求出了2的答案，所以6的二进制表示中，1的个数为1+res[2]=1+1=2。形象表示为：

6  -> 110  ->  1|10  ->  100 + 10 -> 4 + 2
所以结果为4和2的二进制个数之和，因为4是2的整数次幂，所以1的个数肯定为1

上面的思路beat 84%

5.（712:Medium）（非常非常经典题）Minimum ASCII Delete Sum for Two Strings

这道题跟之前那道Delete Operation for Two Strings极其类似，那道题让求删除的最少的字符数，这道题换成了ASCII码值。其实很多大厂的面试就是这种改动，虽然很少出原题，但是这种小范围的改动却是很经常的，所以当背题侠是没有用的，必须要完全掌握了解题思想，并能举一反三才是最重要的。
看到这种玩字符串又是求极值的题，想都不要想直接上DP，我们建立一个二维数组dp，其中dp[i][j]表示字符串s1的前i个字符和字符串s2的前j个字符变相等所要删除的字符的最小ASCII码累加值。那么我们可以先初始化边缘，即有一个字符串为空的话，那么另一个字符串有多少字符就要删多少字符，才能变空字符串。所以我们初始化dp[0][j]和dp[i][0]，分别表示s1为空串和s2为空串的情况。
对于递推公式，我们需要遍历每一个dp[i][j]：当对应位置的字符相等时，s1[i-1] == s2[j-1]，(注意由于dp数组的i和j是从1开始的，所以字符串中要减1)，那么我们直接赋值为上一个状态的dp值，即dp[i-1][j-1]，因为已经匹配上了，不用删除字符。如果s1[i-1] != s2[j-1]，那么就有两种情况，我们可以删除s[i-1]的字符，且加上被删除的字符的ASCII码到上一个状态的dp值中，即dp[i-1][j] + s1[i-1]，或者删除s[j-1]的字符，且加上被删除的字符的ASCII码到上一个状态的dp值中，即dp[i][j-1] + s2[j-1]。事实上这里有第三种情况，那就是同时删除s1[i-1]和s2[j-1]字符，那么dp[i][j] = dp[i-1][j-1] + s1[i-1] + s2[j-1]，但因为我们要保证删除的字符asc码总和最小，所以删除两个字符一定比删除一个字符的asc码大，故在此不考虑该情况。

6.（646:Medium）（非常经典题）Maximum Length of Pair Chain

该题其实就是一道典型的Greedy贪心算法题目，我们将pairs按尾结点从小到大排序，然后从头开始遍历，在尾元素位置相同的情况下，取头元素较大的片段，即pair范围较小的片段，这样才能容纳尽量多的pair（贪心策略）。
当然该题也属于DP问题，一开始很难想出，后来看了Discuss后发现，我们也是从头遍历数组(前提也需要排序)，对于第i个pair，我们搜索前i-1个pairs，看看pair是否能加到前面某些pair后，并更新dp[i]=dp[j]+1，dp[i]存储前i个pair的链的最大长度。用DP解该题有点杀鸡用牛刀。

7.（638:Medium）（非常非常经典题）（Goodle面试题）Shopping Offers

该题采用自顶向下的DP方法，应带备忘录机制，但该题备忘录并不明显，个人感觉是在每层的needs处克隆时采用了备忘。
该题需要注意两点：1.当前的special offer是否与needs的数量满足条件，即不会多买 2.买了当前的special offer会不会省钱
具体的实现思路请参考视频及代码实现备注
参考链接：中文超清晰思路讲解

该题下次复习时应与同学讨论，哪里体现了自顶向下的备忘录机制

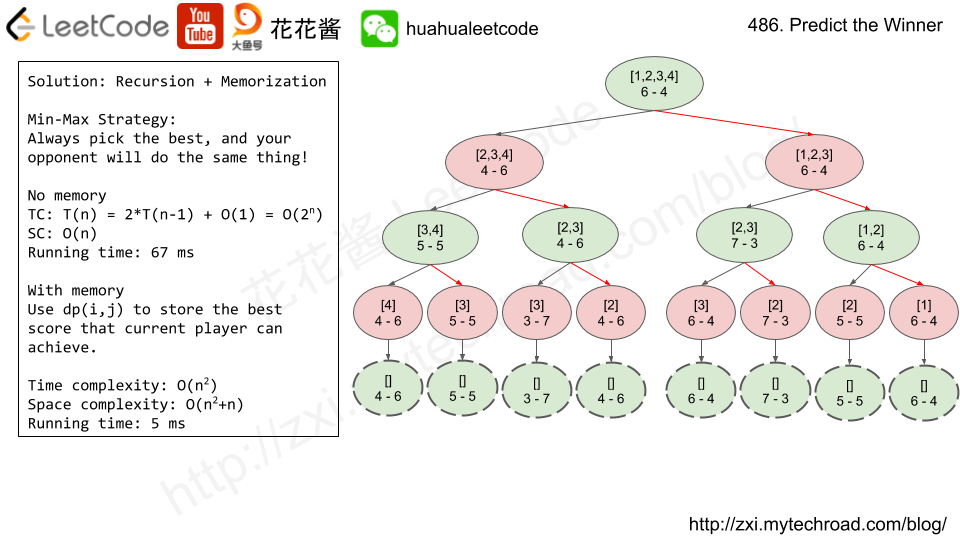
8.（486:Medium）（非常非常经典题）Predict the Winner

博弈类题目，使用minMax思想,使自己分数最大化，对手分数尽量小，递归自顶向下求解。
该题不使用备忘机制同样能通过测试例，只不过耗时相对较长，单纯的比较取数后两players的分数差即可：Math.max(nums[l] - getScore(nums, l + 1, r), nums[r] - getScore(nums, l, r - 1));

从上面的递归树中我们可以发现，对于相同的l、r标记的数组片段，单纯的递归会有多次重复求解，因此我们可以使用备忘机制加快程序速度，对于已经求解过的l至r数组片段，直接返回该数组片段上两者的分数差即可；若没有求解过，则按上面的递归方法求解即可。
参考链接：花花中文视频讲解

9.（650:Medium）（非常经典题）2 Keys Keyboard

首先手写几个答案，可以看到：

n=1, minSteps=0;

　　n=2, 步骤：cp，minSteps=2

　　n=3, 步骤：cpp, minSteps=3

　　n=4, 步骤: cppp或者 cpcp（复制S[2]并粘贴一次），minSteps=4

　　n=5, 步骤：cpppp=c+p*4，minSteps=5

　　n=6, 步骤：c+p*5 或者 cp(cpp) (复制S[2]并粘贴2次) 或者 cpp(cp)(复制S[3]并粘贴1次)， minSteps=5

　　。。。。。

　　n=12, 步骤：c+p*11

　　或者先取得“AA”然后c+p*5（这里5=(12-2)/2），S[n] = S[n/2] + 1+(n-2)/2 = S[n/2] + n/2

　　或者先取得 “AAA”然后c+p*3（这里3=(12-3)/3），S[n] = S[n/3] + 1+(n-3)/3 = S[n/3] + n/3

　　或者先取得“AAAA”然后c+p*2（这里2=(12-4)/4），S[n] = S[n/4] + 1+(n-4)/4 = S[n/4] + n/4

相当于先构造n的一个因子i，然后将该因子复制n/i遍。

从上面可以得出如下规律

　　S[n] = min(S[n/i]+n/i) 其中i为能被n整除的数，n/i是该因子被复制的次数，尝试n的所有因子并取其中最小值得出答案

该题上面的思路是O(n^2)的，应该还可以再化简再提高效率，下次复习时再研究

10.（740:Medium）（非常非常经典题）Delete and Earn

该题可以简化到Leetcode 第198题House Robber。关键题意理解：对于nums = [2, 2, 3, 3, 3, 4]，如果我们选了数字3，则要删除每一个（所有）2和4，之后数组变为[3, 3]，此时如果再选3，并不会删除其他元素，剩余数组变为[3]，再选3，数组变为空，返回结果是3+3+3=9。
那么既然如此，我们可以将上面的例子转化为House Robber的形式，nums' = [0, 0, 22, 33, 4]，nums'[i]代表值为i的数字的总数和，每次若选择nums'数组的一个元素，则相邻元素不能在下一次被选中，相当于被删去。转化后，用House Robber的思路来处理nums'数组即可。
参考视频：花花中文讲解

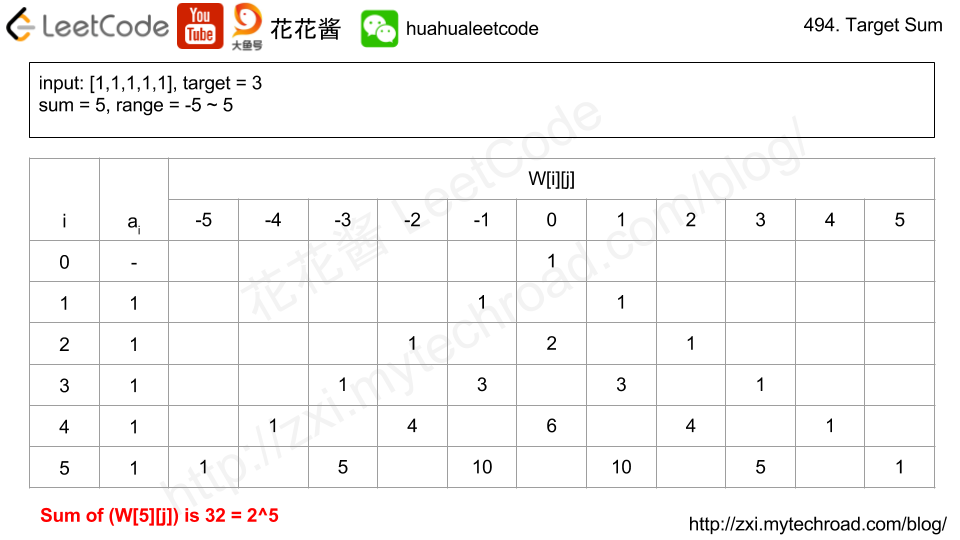
<11>.（494:Medium）（非常非常经典题）Target Sum

该题是一道非常经典的题目，在面试中很可能会考到。该题有多种解法。
第一种解法：DFS，brute force。我们对nums数组中的每个数字，都尝试在其前面添加正号和负号，最后暴力求解，统计数组中各数字组合值为target的情况。(该理解是错误的，我们可以使用带备忘录机制的自顶向下的DP方法，代码见下)

    //带备忘录机制的自顶向下DP解法
    public int findTargetSumWays(int[] nums, int S) {
        if (nums == null || nums.length == 0){
            return 0;
        }
        return helper(nums, 0, 0, S, new HashMap<>());
    }
    private int helper(int[] nums, int index, int sum, int S, Map<String, Integer> map){ //map存储重复的值，there are obvious a lot of overlap subproblems
        String encodeString = index + "->" + sum; //经过之前不同的运算过程到达index的sum值碰巧与之前某一个运算过程的结果相同
        if (map.containsKey(encodeString)){
            return map.get(encodeString);
        }
        if (index == nums.length){
            if (sum == S){
                return 1;
            }else {
                return 0;
            }
        }
        int curNum = nums[index];
        int add = helper(nums, index + 1, sum - curNum, S, map);
        int minus = helper(nums, index + 1, sum + curNum, S, map);
        map.put(encodeString, add + minus);
        return add + minus;
    }

第二种解法：DP。我们使用Vi来表示数组中的前i个数所能求得的和的集合。初始化时

V0 = {0}     //表示前0个数的和为0
Vi = {V(i-1) + ai} U {V(i-1) - ai}
Vn就是nums数组所有数字的组合值之和的集合

根据上面的思路，我们知道数组中数字若全为正号其和为sum，全为负号其和为-sum。若不选数组中任何一个数，则和为0。因此，我们设立一个长度为2*sum+1的数组ways，ways[i]表示我们选择前m个数，其和可能为i的情况数，m = 0,1,...nums.length。可参考下图

那么对于前m个数，其和的情况已经记录在ways数组中，当加入第m+1个数，我们可以根据ways[i+num]求出前m+1个数的和为i+num的情况数，以及ways[i-num]求出前m+1个数的和为i-num的情况数。具体可以参考视频及代码实现。
参考链接：花花中文视频讲解

花花讲解视频分上下两部，我只看了上部，下部没看且会讲效率更高的解法，下次复习时再学习

12.（416:Medium）（非常经典题）Partition Equal Subset Sum

This problem is essentially let us to find whether there are several numbers in a set which are able to sum to a specific value (in this problem, the value is sum/2).
Actually, this is a 0/1 knapsack problem, for each number, we can pick it or not. Let us assume dp[i][j] means whether the specific sum j can be gotten from the first i numbers. If we can pick such a series of numbers from 0-i whose sum is j, dp[i][j] is true, otherwise it is false.
Base case: dp[0][0] is true; (zero number consists of sum 0 is true)
Transition function: For each number, if we don't pick it, dp[i][j] = dp[i-1][j], which means if the first i-1 elements has made it to j, dp[i][j] would also make it to j (we can just ignore nums[i]). If we pick nums[i]. dp[i][j] = dp[i-1][j-nums[i]], which represents that j is composed of the current value nums[i] and the remaining composed of other previous numbers. Thus, the transition function is dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]。形象一点说，dp[i-1][j-nums[i-1]]的意思是，判断在选了第i个数nums[i-1]之后，前i个数的和为j。而在不选第i个数之前，应该前i-1个数经过运算应该能取到j-nums[i-1]这个值
该题我们其实可以将二维数组优化为一维数组，因为在递推过程中，其实我们只用到了dp[i]和dp[i-1]两行。

13.（516:Medium）（非常非常经典题）Longest Palindromic Subsequence

该题与Leetcode String类第647题思路类似，该题可以进行参考。

dp[i][j]: the longest palindromic subsequence's length of substring(i, j), here i, j represent left, right indexes in the string

State transition:

dp[i][j] = dp[i+1][j-1] + 2 if s.charAt(i) == s.charAt(j)

otherwise, dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1])

Initialization: dp[i][i] = 1

注意：i从s.length()-1开始从后往前遍历，是因为在下面的for循环里面要用到i+1，所以bottom-up要用到之前的信息而不是未知的信息，因此从后往前遍历

14.（377:Medium）（非常经典题）Combination Sum IV

该题按之前Combination Sum I、II、III的思路用DFS求解，枚举所有可能的情况，会超时。
正确的思路是动态规划，我们Solution(target) = Solution(target - num) for num in nums。相当于我们将num加在组合和值为target-num的序列前，即构成了target序列。
参考链接：花花DP讲解

<15?>.（309:Medium）（非常非常经典题）Best Time to Buy and Sell Stock with Cooldown

该题与Leetcode Array类第714题 Best Time to Buy and Sell Stock with Transaction Fee非常相似，但涉及的状态会更多。
该题仍然用s0表示未持有股票状态，s1表示持有股票状态，因为题目中设计到cooldown冷却状态，所以引入rest用以表示，而且只有在s0状态卖出股票时才能进入cooldown。因此为了便于分析，这里要求s0只能表示卖出股票，不能表示维持原未持有股票状态不变。后一个维持未持有股票的情况在rest的递推过程中来表示，因此状态划分还是完全的。
递推关系如下：

int t = s0;
s0 = s1 + prices[i];
s1 = Math.max(s1, rest - prices[i]);    //维持原状或cooldown后买入
rest = Math.max(rest, t);	//取当天不买入不卖出和cooldown的最大值

参考链接：花花中文讲解

该题自己的分析感觉并不恰当，状态转移关系还是有一些不理解，为什么这样划分状态是完备的，下次复习时需与同学请教。且该题的状态数还可以继续简化为2个

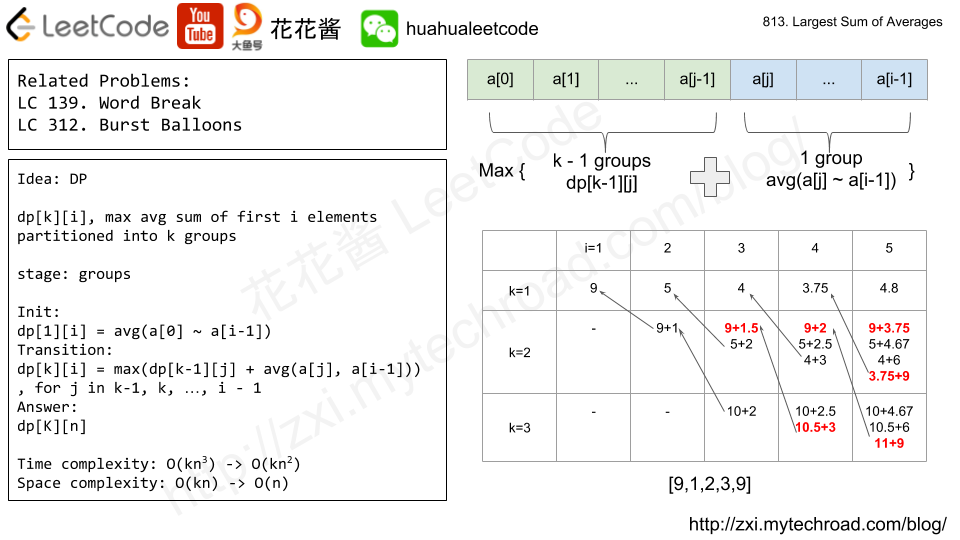
16.（813:Medium）（非常非常经典题）Largest Sum of Averages

寻找最佳分割点问题，与Leetcode 第139、312题相似。

该题的思路是，将0~i-1个数字以第j个数字为分界线，前j个元素分为k-1组，第j+1至i个数字分为单独的一组。用dp[k][i]表示将前i个数字分为k组情况的最大平均值之和。递推公式为dp[k][i] = max(dp[k-1][j] + avg(a[j],a[i-1]))，最佳划分点j需要通过暴力求解才能得出（导致时间复杂度为O(n^2)）。通过Bottom-up从k=1开始求解至K，从i=1开始求解至n，最后返回dp[K][n]即得答案。
参考链接：花花中文讲解

17.（688:Medium）（非常经典题）Knight Probability in Chessboard

我们设置一个N*N的二维数组，代表走了k步后落在棋盘上各个位置的路线数量，dp[k][i][j]表示从初始位置走k步到达(i,j)路线数，它应该是在dp[k-1][x][y]的基础上，从(x,y)向八个方向前进，有某一方向到达(i,j)的路线数之和。具体参看代码实现及参考视频。
参考链接：花花讲解视频

18.（300:Medium）（非常经典题）Longest Increasing Subsequence

该题和之前做过的一道动态规划题目非常相似(忘记是哪道了)。我们设置一个长度为nums.length的数组dp，dp[i]表示0..i个数字序列中，以nums[i]结尾的最长升序序列长度，递推公式如下，比较nums[i]以前的元素nums[0..i-1]，若nums[i]>nums[j]，则dp[i]应更新为以nums[j]结尾的序列长度值+1或维持不变。时间复杂度O(n^2)。（beat 45%）

for(int i = 1; i < nums.length; i++) {
	for(int j = 0; j < i; j++) {
	   if(nums[j] < nums[i])
	      dp[i] = Math.max(dp[i], dp[j]+1);
	}	
}

该题还有O(nlogn)的解法，下次复习时再学习研究

19.（474:Medium）（非常非常经典题）Ones and Zeroes

题目和0-1背包问题大同小异，区别是这里限制0和1个数，而0-1背包问题限制总重量，算是动态规划的经典题目，可以了解一下0-1背包问题
这里用dp[i][j][k]表示前i个字符串在0个数不超过j、1个数不超过k时最多能选取的字符串个数。统计第i个字符串中0和1个数分别为cnt0和cnt1，如果取第i个字符串则dp[i][j][k] = dp[i-1][j-cnt0][k-cnt1] + 1，如果不取第i个字符串则dp[i][j][k] = dp[i-1][j][k]，取两者大的作为dp[i][j][k]的值。由于dp[i][j][k]只与dp[i-1][*][*]相关，所以这里可以重复使用m*n个数据将空间复杂度降为O(m*n)，利用滚动数组，只需在遍历时从后向前遍历即可。
数组从后向前遍历的原因：我们在代码实现过程中，需要基于上一轮的数组信息来更新本轮的数组值。假设我们当前要更新memo[3][2],需要用到memo[1][2]（上一轮的信息），如果从头开始遍历，则在求解memo[2][3]时，memo[1][2]已经变成本轮的已更新值，显然是不正确的。
具体实现参看代码实现及注释。

<20>.（698:Medium）（非常经典题）Partition to K Equal Sum Subsets

该题使用递归解法，在当前操作不可行进行向前回滚的时候用到了备忘机制。
首先我们将整个数组排序，并且比较最后一个元素是否比每个组合的目标值target还大，若大于则说明不可能构成元素和为target的组合，直接返回false。否则说明可能可以构成符合条件的分组，我们从后往前处理数组元素，当subsets[i]+selected<=target时，说明该元素可能可以放到第i个subset中，若后续的放置均满足条件则返回true；否则将selected从第i个subset中取出，放入i+1、i+2...的满足条件的subset中。
具体的思路请参看代码实现及参考视频。
参考链接：中文视频讲解

不明白为什么属于DP问题，可能还有DP解法，下次复习时再研究、参看discuss

21.（375:Medium）（非常经典题）Guess Number Higher or Lower II

It is actually confusing that the example shown in the problem description is not the best stragety to guess the final target number, and the problem itself is asking for the lowest cost achieved by best guessing strategy. The example description should be updated.

---POSSIBLY, it can also add some example about the BEST Strategy---

The example description should be:

first introducebest strategyto guess:

for one number, like 1, best strategy is 0$
for two number, like 3,4, best strategy is 3$, which can be understood in this way: you have two way to guess: a) start by guess 4 is the target, (the worst case is) if wrong, you get charged $4, then immediately you know 3 is the target number, get get charged $0 by guessing that, and finally you get charged $4. b) similarly, if you start by 3, (the worst case is) if wrong, you get charged $3, then you immediately know that 4 is the target number, and get charged $0 for guessing this, and finally you get charged $3. In summary:

range ---------> best strategy cost

3, 4 ---------> $3

5, 6 ---------> $5

...
for three number, the best strategy is guess the middle number first, and (worst case is) if wrong, you get charged that middle number money, and then you immediately know what target number is by using "lower" or "higher" response, so in summary:

range ---------> best strategy cost

3, 4, 5 ---------> $4

7, 8, 9 ---------> $8

...
for more numbers, it can simply be reduced them into smaller ranges, and here is why DP solution make more sense in solving this.

suppose the range is [start, end]

the strategy here is to iterate through all number possible and select it as the starting point, say for any k between start and end, the worst cost for this is: k+ max(DP( start, k-1 ), DP(k+1, end ))(Since we don't know whether high or low, just pick worst case. 现在的前提是，target可能位于[start,k-1]及[k+1,end]中花费较大的区间，我们现在求得是比较general的花费，并没有指定target,我们认为它总是处于花费较大的区间，而在此基础上，我们要求k，满足选取的k在[start,end]中是使总体花费最小的一个数) , and the goal is minimize the cost, so you need the minimum one among all those k between start and end.

参考链接：中文博客讲解， Minmax 算法讲解， Tic-tac-toe minmax算法讲解

该题题意比较难懂，下次复习时需要仔细看上边的题目英文解析，在实现时是使用的top-down解法还比较易理解，但是bottom-up解法感觉在计算localMax = k + Math.max(table[i][k-1], table[k+1][j])时，table[k+1][j]并没有计算出来，不知道为什么，需与同学讨论

22.（213:Medium）（非常非常经典题）House Robber II

我们通过Leetcode 第198题House Robber已经了解如何抢一排房子，从而获取最大利益的算法策略。该题中，房子是连成一个环的，最后一个房子的抢或不抢会直接影响到第一个房子的决定。为了继续利用地198题的算法，我们应该将环转换为链。
因为当最后一个房子决定不抢的时候，我们可以对第一个房子作出任意决定，原题转化为1..n-1个房子链；同理当第一个房子决定不抢的时候，我们可以对最后一个房子做出任意决定，原题转化为2..n个房子链。
当然还有一种思考方式是，我们确定抢、不抢第一个房子：当确定抢第一个房子的时候，我们只能从第三个房子开始做出决策，房子链变为3..n-1个房子，且最后总的收益还要加上第一个房子的收益，思考过程更复杂，且在考虑数组越界方面的处理会相对复杂（考虑整个房子的数量n只有2或3的时候），所以不采用这样的分类策略思考方式。
具体细节思路参看代码实现及参考链接。
参考链接：Simple AC solution in House Robber II : Java in O(n) with explanation

23.（467:Medium）（非常经典题）Unique Substrings in Wraparound String

这道题遍历p的所有子字符串会TLE，因为如果p很大的话，子字符串很多，会有大量的满足题意的重复子字符串，必须要用到trick，而所谓技巧就是一般来说你想不到的方法。
这里递推的方法是：假如现在有以d结尾的abcd子字符串，那么该字符串中以d结尾的bcd、cd、d一定均在s中，所以只需要找以当前字符结尾的最长子字符串即可，它的长度就是该字符串及以当前字符结尾的子字符串在s中存在的个数。
注意：题目中说到find out how many "unique" non-empty substrings of p are present in s。所以重复的子字符串不能多次计算。我们应取以某一个字符X结尾的最长子字符串长度作为该字符结尾的最终结果。具体实现思路请参看代码实现。

<24>??？.（790:Medium）（非常经典题）Domino and Tromino Tiling

该题没看懂题意，请参看参考链接。
参考链接：参考discussion 参考视频教程

25.（139:Medium）（非常非常经典题）Word Break

该题采用top-down的自上而下DP递归求解方法。按上图所示，我们尝试将当前待处理的字符串进行分割，我们首先会判断分割点右半部分是否在wordDict中，若存在，则递归判断左半部分是否可以被分割成功；若该分割不成功，则将分割点继续后移一位，继续尝试是否能分割；若分割点移动到末尾，则返回false。
注意：将上图中dict的判断和递归函数交换一下顺序可以减少递归深度，提高效率
具体细节参考"代码实现"及"参考链接教程"。
参考链接：TOP-DOWN递归DP方法
该题用Bottom-up方法的DP求解非常简单，参看下面的代码：

public boolean wordBreak(String s, Set<String> dict) {
      if (s == null || s.length() == 0) return false;

      int n = s.length();

      // dp[i] represents whether s[0...i] can be formed by dict
      boolean[] dp = new boolean[n];

      for (int i = 0; i < n; i++) {
        for (int j = 0; j <= i; j++) {
          String sub = s.substring(j, i + 1);

          if (dict.contains(sub) && (j == 0 || dp[j - 1])) {
            dp[i] = true;
            break;
          }
        }
      }

      return dp[n - 1];
}

提醒

DP问题是有自上而下递归求解的，所以遇到动态规划问题，不要只局限于bottom-up，只能从底层开始求解。有时，top-down带备忘机制的递归DP求解方法更简单，更易被理解。

26.（673:Medium）（非常非常经典题）Number of Longest Increasing Subsequence

该题与第18题（300）Longest Increasing Subsequence思路相近，只是需要统计最长上升子序列的数量。解决办法是：我们将dp数组设为2维，dp[i][0]代表前0至i个元素中最长序列长度,dp[i][1]代表具有该长度的上升子序列个数。计数原则如下：

for(int i = 1; i < nums.length; i++) {
	for(int j = 0; j < i; j++) {
		if(nums[j] < nums[i]) {
			if(dp[j][0] + 1 == dp[i][0])	//有重叠，增加以相同元素结尾的相同长度序列重叠个数
				dp[i][1] += dp[j][1];
			else if(dp[j][0] + 1 > dp[i][0]) {	//没有重叠，更新长度及对应新序列个数
				dp[i][0] = dp[j][0] + 1;
				dp[i][1] = dp[j][1];
			}
		}
	}
	maxLen = Math.max(maxLen, dp[i][0]);
}

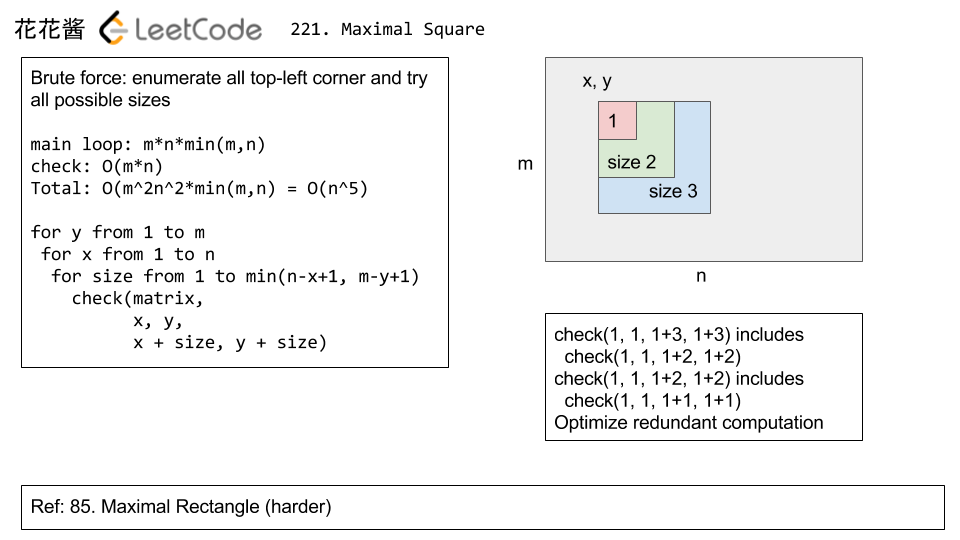
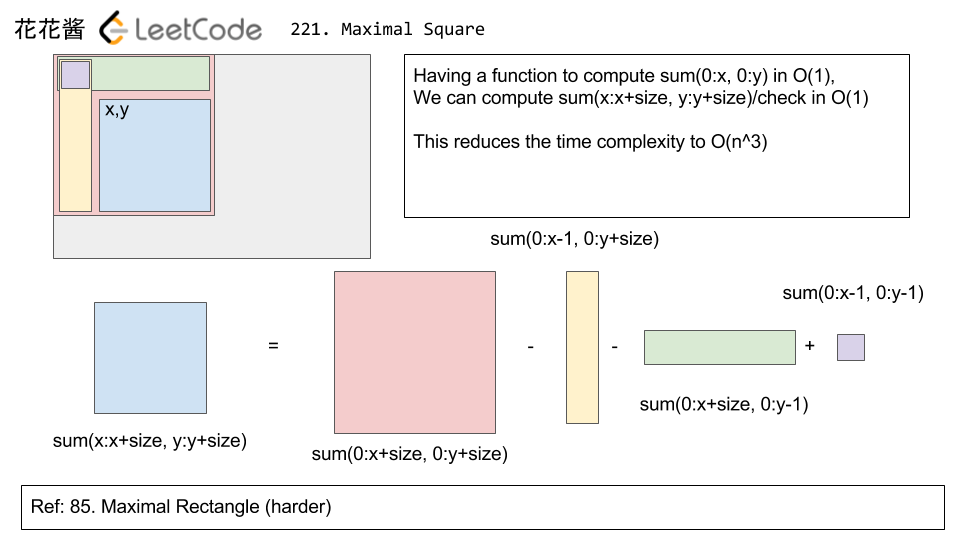
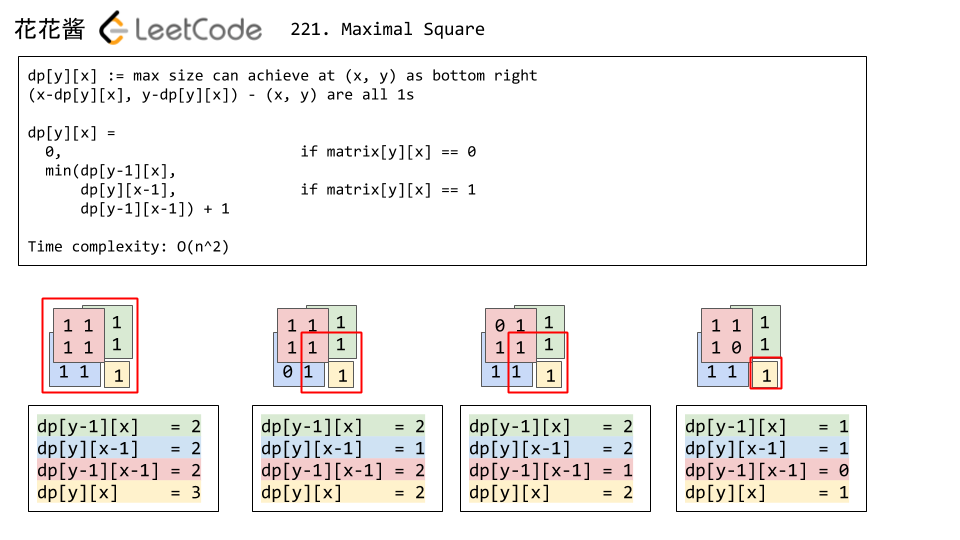
<27>.（221:Medium）（非常非常经典题）Maximal Square

该题是Leetcode 85题的简化版，思路类似，但难度更低。该题有两种解法：一种是比较general的，适合求最大面积，也适合求最小面积；另一种是利用所给矩阵的元素只有0、1来进行求解。

第一种解法请参看上图，是由Brute force演变来的。对于暴力解法，我们的思路是，遍历每一个坐标点作为正方形的左上方顶点，然后依次从1开始扩大正方形的边长，判断在边长范围内是否为全1。固定当前顶点选取最大面积的正方形，之后再移动顶点遍历整个矩阵，取最大面积即是答案。整个矩阵遍历过程需要O(mn)，在固定顶点不动，增大边长判断边长范围内是否为全1又需要O(mn*min(m,n))的时间复杂度，所以Brute force总体上需要O(n^5)时间复杂度。优化的关键是减少"判断正方形是否为全1"的时间，将其从O(n^3)降低为O(n)。那么如何利用DP降低"check全1"的时间复杂度呢，我们参看下面的两个图：

从上面的第一张图可以看出，若要求右下角的小正方形面积，需要大矩形面积-两个小矩形面积+重叠面积；换句话说，若要使用bottom-up，我们应该是已知小矩形面积，来求大矩形面积，参看上面的第二张图中的公式，dp[y][x]表示区间在0-x且0-y范围内的1的总和，其中matrix[y][x]是坐标在(x,y)的边长为1的小正方形内的1的个数。因此，得到上面第二章图中的递推公式：dp[y][x] = dp[y][x-1]+dp[y-1][x]-dp[y-1][x-1]+matrix[y][x]，那么当正方形的面积与正方形内1的总和相等时，说明全部都是1。此外有一个小trick：在固定正方形顶点，改变正方形边长的时候，边长应由大到小进行尝试，这样当较大边长内为全1时，不必再尝试较小的边长了。具体的实现细节及思路参看代码及参考链接。
第二种解法是利用矩阵元素只有0和1的性质，我们设立dp数组变量，dp[y][x]作为以坐标(x,y)为右下方顶点的正方形最大面积，我们通过观察下图中给出的示例，若要求dp[y][x]，只需要比较dp[y][x-1]、dp[y-1][x]及dp[y-1][x-1]的值即可，取其中最小的值加1（若(x,y)坐标为1）即为dp[y][x]的值，若(x,y)处为0，则dp[y][x]=0。具体的实现细节及思路参看代码及参考链接。

参考链接：花花两种方法中文讲解视频

第二种方法的效率要高于第一种方法的效率

该题通俗一点来理解：除去边界（即第一行与第一列），对于任意一个matrix[i][i]，他所处的正方形大小应该由前一层决定：左边(matrix[i][j-1])，上边(matrix[i-1][j]),左上（matrix[i-1][j-1])决定。同样的，我们也需要一个结果矩阵 sizes[M][N] 记录每个对应点所处的方形层数（正方形边长）。很明显，对于层数计算，并没有获取前一层的都处于的方形层数，要知道，假设在[i][j]为止是属于3*3的方形，那么必然有点[i-1][j]，[i][j-1], [i-1][j-1]这3个都至少属于2*2的方形，可能用图示更清楚：

left: top: left top:

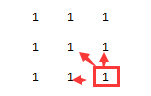
参考链接：想透彻理解本题必须看的讲解

28.（576:Medium）（非常非常经典题）Out of Boundary Paths

感觉该题和第17题（688）Knight Probability in Chessboard思路类似。区别在于，第17题（688）必须走K步，而该题可以走小于等于N步。
我们只能从(i-1,j)、(i+1,j)、(i,j-1)、(i,j+1)四个方向走一步到(i,j)，所以可得到如下递推式：dp[s][i][j]=dp[s-1][i-1][j]+dp[s-1][i+1][j]+dp[s-1][i][j-1]+dp[s-1][i][j+1]，其中dp[n][x][y]代表从边界走n步到达(x,y)的路径数。需要注意，如果(i,j)与边界相邻，则从边界到(i,j)只需走一步。
注意：因为该题数组只用到s与s-1，所以可以利用滚动数组降维。
参考链接：花花中文讲解

29.（801:Medium）（非常非常经典题）Minimum Swaps To Make Sequences Increasing

用DFS会超时，应该使用DP，用"小规模"的解去求"规模大1"的问题的解。
不能只保存从0-i交换的最小次数这一个状态信息，否则会导致后边推理逻辑出现问题。因此，我们除了保存对于已知的0-i交换的最小次数外，还需记录第i个元素是否被交换这一状态信息。故设两个长度为n的数组keep、swap，表示i位置的元素是否交换或未交换。
DP考虑索引位置i及i-1的元素：

当A[i] > A[i - 1] && B[i] > B[i - 1]时

（1）如果我们不交换A[i]和B[i]，那么序列0-i也是严格单调递增的，所以有keep[i] = keep[i - 1]

（2）当然，我们也可以同时交换A[i-1]和B[i-1]及A[i]和B[i]，保证原来的相对位置不变，仍满足递增的条件，swap[i] = swap[i - 1] + 1

当B[i] > A[i - 1] && A[i] > B[i - 1]时，是交叉大于的情况

（1）我们可以交换i位置的A[i]和B[i],而i-1位置保持不变，同时为了和上面的第一个判断条件中处理结果进行比较，需要用到min函数，swap[i] = Math.min(swap[i], keep[i - 1] + 1)

（2）我们也可以交换i-1位置的A[i-1]和B[i-1],i位置保持不变，道理同上，keep[i] = Math.min(keep[i], swap[i - 1])

注意：1.这里的A[i]、A[i-1]、B[i]、B[i-1]均是原来输入数组的元素，并没有发生真正的交换而改变，我们只是用keep和swap数组来假设i位置上的元素是否进行了交换 2.注意到每次计算时，只需要i和i-1的状态信息，所以可以使用滚动数组来降维，空间复杂度从O(n)降到O(1)。
参考链接：花花中文讲解

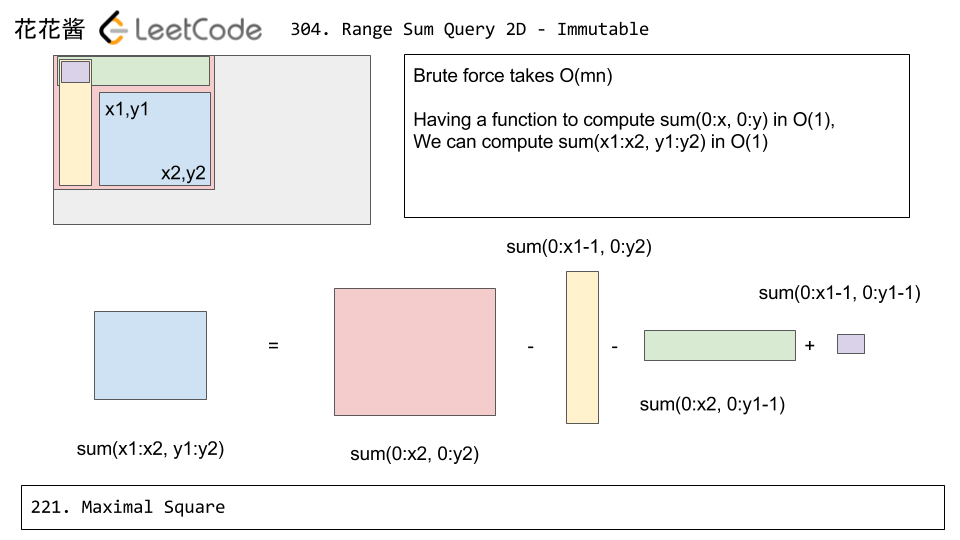
30.（304:Medium）（非常经典题）Range Sum Query 2D - Immutable

设立一个sumMatrix矩阵，在预处理的时候，sumMatrix[i][j]代表输入的matrix矩阵中第i行，从0到j的元素之和。在调用sumRegion函数，求(m,n1)到(m,n2)的元素和时，直接由sumMatrixp[m][n2]-sumMatrix[m][n1-1]求出。
该题的标准解法示意图如下，具体思路视频教程请参看：花花中文讲解视频

下面是建立DP数组的思路，时间复杂度O(mn)

下面是求解的思路，时间复杂度O(1)

该题不让改变matrix矩阵，上面的思路也没有改变，只是新建了一个数组来储存元素和。但可能不满足题目中某个条件，虽然beat 100%，但下次复习时应参看discuss中其他人的思路

31.（322:Medium）（非常经典题）Coin Change

该题有两种思路，一种是使用DP，一种是使用DFS+Greedy。这里讲解DFS+Greedy的方法，效率更高，且更易理解。
总的思路：我们每次都尽量使用面值较大的coin，同时使用数量较多的面值较大的coin，从而保证总的数量最少。当当前的count数量已经大于之前的count数量，则没有必要进行更深层次的递归（剪枝），因为该路径已经不会出现更优的解。
参考链接：花花中文视频讲解

DP动态规划的解法下次复习时可以参看，但个人感觉没有必要使用DP，DFS就挺好的

32.（464:Medium）（非常非常经典题）Can I Win

该题和第8题（486） Predict the Winner一样，都是Game类问题，需要用到MinMax决策思想。这种Game类题目都有相似的解题方法，那就是使用Top-down的DP带备忘录的递归解法，使用备忘录来存储已经计算过的重复子问题答案，从而大大降低时间复杂度。
对于该题，我们用0或者1来代表当前选手在当前状态下的输赢情况，因为每人可以从[1,maxChoosableInteger]中选一个数，而每个数都有两种情况“选”或“不选”，所以用二进制表示的话总共有2^maxChoosableInteger种状态。又因为在没有分出输赢的情况下，12X和21X对于第三次选择X产生的影响相同，所以我们不必计较数字选择的先后顺序，所以对于maxChoosableInteger=2时，总共有00、01、10、11四种状态，对于第i位，代表着数字i+1的情况。因此，我们初始化状态为0，每次遍历所有的可选数字，如果当前的选择最终不会使自己获胜，则选下一个符合条件的数字；当做出任何选择都会使自己失败时，才做出memo[当前状态]=0的判别。
具体的思路请参看代码实现注释及参考链接。
参考链接：花花中文视频讲解

<33>.（312:Hard）（非常经典题）Burst Balloons

该题使用DP求解，bottom-up，但也可以使用top-down，具体请参看参考链接，下面以bottom-up进行讲解。
从示例中我们可以看到，并不是当前状态下某个气球被扎破所获得的coin最大，最后的结果就最大。对于该题，DP的递推式为dpdp[i][j] = dp[i][k-1] + nums[i-1]*nums[k]*nums[j+1] + dp[k+1][j]，dp[i][j]表示只使用i~j气球能获取的最大分值。对于递推式的理解：对于i~j气球，我们寻找某一个气球k，我们先打破i~k-1的气球和k+1~j的气球，最后才打破气球k，在打破气球k时的计算公式为nums[i-1]*nums[k]*nums[j+1]。具体的细节和解释可以参看代码和参考链接视频。
参考视频：花花中文讲解

该题对于递推关系的由来还是有一些不解，不知道递推式是怎么得来的。下次复习时请教同学

34.（410:Hard）（非常非常经典题）Split Array Largest Sum

该题有两种方法：DP和Binary Search，而DP又分为Top-down和Bottom-up，下面以Dp的bottom-up进行讲解。

DP思路的递推关系：将前i个数分成m组，等价于将前k个数分成m-1组，而k+1到i个数单独分成一组(0<=k<j)。我们用dp[i][j]表示将前j个数分为i组，又因为我们要将分组后最大值最小化，递推关系式为：dp[i][j]=min(max(dp[i-1][k],sum(nums[k+1~j])))。初始化变量是将前i个数分为1组，即是前i个数的和。
参考链接：花花DP+Binary Search讲解视频

该题的Binary Search方法效率会比DP更高更巧妙，下次复习时再参看学习

35.（514:Hard）（非常经典题）Freedom Trail

dp[i][j] is conceptually the minimum steps needed to to complete key[i:]（表示key中第i个及以后的所有字符）, while starting at ring[j]. (ignore the steps for spelling, which is added at the end => 'm').
Thus, in the inner-most loop, we looking for all indexes 'k' in ring s.t. ring[k] == key[i]. We try to go to all such index 'k' from 'j', calculate the minimum distance to get there => 'step', and the total cost will be 'step' + dp[i + 1][k]', where the later is the minimum cost of constructing the remaining key[i+1:] starting from 'k'.
代码及注释参考如下：

public int findRotateSteps(String ring, String key) {
    int n = ring.length();
    int m = key.length();
    int[][] dp = new int[m + 1][n];	//这里第一维的长度是m+1，要比key的长度多1，是因为在下面的最内层循环时，当i=m-1指向key的最后一个字符时，需要用到i=m，这里只是为了方便处理
        
    //i指向key，j指向ring
    for (int i = m - 1; i >= 0; i--) {	//i从m-1最后往前处理，是因为在最内层for循环中，dp[i][j]的更新需要用到dp[i+1][k]
        for (int j = 0; j < n; j++) {
            dp[i][j] = Integer.MAX_VALUE; //初始化从转盘的j位置是无法找到key的第i个字符的
            for (int k = 0; k < n; k++) {
                if (ring.charAt(k) == key.charAt(i)) {
                    int diff = Math.abs(j - k);  //k与j的距离
                    int step = Math.min(diff, n - diff);  //比较正时针转步数比较少，还是逆时针转步数比较少
                    dp[i][j] = Math.min(dp[i][j], step + dp[i + 1][k]); //当前key中第i个字符的拼写还要综合考虑key中之后字符的拼写
                }
            }
        }
    }
        
    return dp[0][0] + m;  //m是press button的步数
}

36.（847:Hard）（非常经典题）Shortest Path Visiting All Nodes

该题算是图论问题，因为要寻找最短路径，所以我们使用BFS来进行求解。此外该题还可以使用DP思路，但接下来以BFS进行讲解。与以往的BFS问题不同，该题目中，对于之前已经访问的结点可以多次遍历，而以前的图论问题只是将已访问结点作标记，不重复访问。
我们用set储存之前已遍历过的状态（包括已遍历结点及当前结点所处位置），用queue存储遍历的路径、当前结点位置及已付出的代价（这里的cost代价是访问路径上经过的结点个数，包括第一次遍历的新节点及已访问的重复结点）。因为搜索起点不固定，因此我们要尝试以每个结点为起点，寻找最先遍历完所有结点的路径。
对于n个结点的图，我们以长度为n的二进制01序列来表示每个结点的遍历情况，1表示已遍历，0表示未遍历，第i位的数值代表第i个结点的遍历状态。graph[i]表示结点i的相邻结点集。
实现时，为了减少集合中判定某个路径及所在位置是否在之前出现过，我们使用hashCode()方法来大大提高运行效率。若不使用hashCode()函数，则会被判为超时。具体实现细节及思路参看代码实现。
参考链接：花花中文讲解(没怎么看，最好参看实现代码)

<37>.（546:Hard）（非常经典题）Remove Boxes

该题可能使用top-down的递归dp解法较易理解，设置三维数组来作为备忘录，dp[i][j][k]表示在序列i~j盒子序列上，若从右往左相同颜色的盒子为k时所能获得的最大points数量。该题较难，建议参看参考链接及代码注释进行理解，递推式部分并没有理解透彻。
参考链接：中文讲解，不是很懂

该题没懂，第二种情况下的递推式不知道由来，下次需请教同学

38.（691:Hard）（非常非常经典题）Stickers to Spell Word

该题使用自上而下带备忘录机制的递归DP解法。我们首先需要统计每一个sticker和target字符串的各字母词频。
递归推导的思路：我们尝试用当前的sticker来构建当前的target字符串，对于剩余无法构建的字符，我们将其拼接成新的字符串序列s，然后进行更深层次的递归，让其他的sticker或其自身在下一层来构建s，然后按此递归下去，直到target被完全构建，某一层的s变成空串""。因为我们并不是定义前i个stickers构成target的前j个字符，而是只关注字母词频，不在意其顺序，所以并不知当前的字符串是什么（如appleapple变成了lea或者eapp），因此不能按照dp[i][j]的方式来定义备忘录。那么，这里只能使用HashMap来当作备忘录，key是已构建的字符串，value是构成该字符串所需的最少stickers数量。
注意：这里用到的一个剪枝方法，If the target can be spelled out by a group of stickers, at least one of them has to contain character target[0]. So I explicitly require next sticker containing target[0], which significantly reduced the search space.
具体思路请参考实现代码及注释，非常详细。

关于第38题（691）的感想

由第38题可见，我们在求解dp问题时，对于dp递归变量不一定只能以"数组"的形式来存储，还可以使用"HashMap"。但"HashMap"针对的问题，可能是在程序运行过程中并不知道当前所处理的子问题是什么，它不像"数组"那样，明确知道我们求解的子问题是从某一位置到另一个位置的中间序列。

<39>.（664:Hard）（非常经典题）Strange Printer

该题可以使用top-down和bottom-up两种DP解法，下面以bottom-up为例进行讲解。
设立二维数组dp[i][j]表示最少的print次数产生字符串第i到j个字符序列，递推逻辑是：我们将第i到j个字符序列分为i到k-1和k到j两个部分进行组成。在拼接两个部分时，如果第一个部分的最后一个字符和第二个部分的最后一个字符相等，则减少一次print（例如aba，可先产生aaa，然后再产生aba；而不是a、ab、aba）。对每一个i到j字符序列，寻找合适的最小分割点k，将print次数存入dp[i][j]。
具体细节可以参考代码实现及注释。

在递推时，两部分的合并为什么只能同时考虑头(i和k)，或同时考虑尾(k-1和j)，不能交叉(i和j或k-1和k)呢?不明白，下次复习时请教同学

40.（403:Hard）（非常非常经典题）Frog Jump

该题一开始准备尝试top-down的递归DP解法，但发现逻辑很混乱。于是采用bottom-up方法。
因为我们并不是从0到最后一个石头中间每一个unit都是可达的，所以不建议使用数组，因此和之前第38题(691)类似，这里使用HashMap来存储状态信息。HashMap的key是石头的位置，value是之前的能到达该石头所走过的laststep步数集。在0位置的石头时，默认走过的步数为0，这样下一步只能走一步，这是由题目条件所得出的。之后我们从前往后遍历每一个石头，取出到达当前石头的lastStep，求出nextStep并判断能否到达之后的某一个石头。若可以则将到达之后石头所用的步数存入对应的set集合中，否则在[lastStep-1,lastStep+1]的范围内调整下一步的大小继续尝试。当存在能够到达最后一个石头的步数时，则说明从0位置开始出发，最后一个石头是可达的，返回true；否则返回false。
具体的实现细节参看代码注释及参考视频。
参考链接：中文思路视频讲解

41.（354:Hard）（非常非常经典题）Russian Doll Envelopes

该题因为涉及到边长的大小关系，所以首先按高度进行排序。设立一维dp数组，dp[i]表示第i个信封最多能嵌套的信封数量。然后从头开始遍历信封数组，将其嵌套信封先初始化为dp[i]=1，之后，设立变量j(0<=j<i-1)来遍历比当前信封高度小的之前的信封。只有当前信封的高度和宽度都比之前的信封大时，才能嵌套，dp[i]更新为小的信封能嵌套的个数加上大信封其本身，即dp[i] = max(dp[i], 1 + dp[j])。
具体细节请参看代码实现及注释。

42.（600:Hard）（非常非常经典题）Non-negative Integers without Consecutive Ones

该题分为两部分：1.求n位无连续1的二进制数个数 2.将满足条件的数中大于num的数字去掉即得答案
对于如何求n位无连续1的二进制个数，需要使用DP动态规划求解，原理请参看视频(求二进制无连续1个数视频讲解)。设两个dp数组dp0和dp1，dp0[i]表示第i位为0的无连续1的二进制数个数，dp1[i]表示第i位为1的无连续1的二进制数个数。递推公式为：

 dp0[i] = dp0[i - 1] + dp1[i - 1]; //当第i位为0时，i-1位既可以是0，也可以是1。 
 dp1[i] = dp0[i - 1];  //当第i位是1时，i-1位只能是0
 对于n位的二进制数，总共符合条件的无连续1的二进制个数为: dp0[n-1]+dp1[n-1]

之后就是将满足条件的数中大于num的数字去掉。请参看下面的英文解释：

if bit[i] == 1
        if bit[i + 1] == 0, there's no solutions in res that is larger than num, we go further into smaller bit and subtract.
        if bit[i + 1] == 1, we know in those res solutions it won't have any consecutive ones. when bit[i + 1] == 1, in one[i + 1], the i-th bit in valid solutions must be 0, which are all smaller than 'num', we don't need to check smaller bits and subtract, so we break form the loop.

if bit[i] == 0
        if bit[i + 1] == 1, there's no solutions in res that is larger than num, we go further into smaller bit and subtract.
        if bit[i + 1] == 0, we know zero[i + 1] includes solutions of i-th == 0 (00***) and i-th bit == 1 (01***), we know the i-th bit of num is 0, so we need to subtract all the 01*** solutions because it is larger than num. Therefore, one[i] is subtracted from res.

for (int i = n - 2; i >= 0; i--) {
     if (sb.charAt(i) == '1' && sb.charAt(i + 1) == '1') break;  //此时num中出现连续1，而result中不可能出现连续1的数，所以剩余的result中二进制数一定比num小
     if (sb.charAt(i) == '0' && sb.charAt(i + 1) == '0') result -= dp1[i]; //高位和低位均为0，那么应将低位为1的二进制数去掉，它们大于num
}

<43???>.（552:Hard）（非常非常经典题）Student Attendance Record II

该题可以分为在无A的前提下以L结尾、以P结尾和含一个A，总共三种情况。思路在使用DP思想的基础上有很多种，可以参考链接：小Fu讲解，但个人感觉思路并不清晰

该题思路并没有理解，网上详细清晰的思路也不多，下次复习时与同学请教

44.（472:Hard）（非常非常经典题）Concatenated Words

该题首先要理解Leetcode 139题Word Break的解题思路，在139题的基础上，我们只需要将单词数组按长度从小到大排序，然后逐个按139题的思路进行处理即可（DP）。
简单来说，我们设立一个preWords集合保存当前单词以前的所有比他长度小的单词集合，对每一个单词，我们设立长度为n+1的dp数组，dp[j]表示word的0~j-1子字符串是否能由之前单词构成，然后从0开始寻找合适的分割点，看看dp[j]=ture，preWords是否含有word.subString(j,i)成立。然后将指针后移到下一个单词，将之前的单词加入到preWords集合中。

上面讲解的是DP解法，该题好像还可以用DFS进行求解，下次复习时可以参考discuss学习一下

<45>.（446:Hard）（非常非常经典题）（建议参看英文逻辑）Arithmetic Slices II - Subsequence

决定要用DP了，那么首先就要确定dp数组的定义了，刚开始我们可能会考虑使用个一维的dp数组，然后dp[i]定义为范围为[0, i]的子数组中等差数列的个数。定义的很简单，OK，但是基于这种定义的递归式却十分的难想。我们想对于(0, i)之间的任意位置j，如何让 dp[i] 和 dp[j] 产生关联呢？是不是只有 A[i] 和 A[j] 的差值diff，跟A[j]之前等差数列的差值相同，才会有关联，所以差值diff是一个很重要的隐藏信息Hidden Information，我们必须要在dp的定义中考虑进去。所以一维dp数组是罩不住的，必须升维，但是用二维dp数组的话，差值diff那一维的范围又是个问题，数字的范围是整型数，所以差值的范围也很大，为了节省空间，我们建立一个一维数组dp，数组里的元素不是数字，而是放一个HashMap，建立等差数列的差值和当前位置之前差值相同的数字个数之间的映射。我们遍历数组中的所有数字，对于当前遍历到的数字，又从开头遍历到当前数字，计算两个数字之差diff，如果越界了不做任何处理，如果没越界，我们让dp[i]中diff的差值映射自增1，因为此时A[i]前面有相差为diff的A[j]，所以映射值要加1。然后我们看dp[j]中是否有diff的映射，如果有的话，说明此时相差为diff的数字至少有三个了，已经能构成题目要求的等差数列了，将dp[j][diff]加入结果res中，然后再更新dp[i][diff]，这样等遍历完数组，res即为所求。
我们用题目中给的例子数组 [2，4，6，8，10] 来看，因为2之前没有数字了，所以我们从4开始，遍历前面的数字，是2，二者差值为2，那么在dp[1]的HashMap就可以建立 2->1 的映射，表示4之前有1个差值为2的数字，即数字2。那么现在i=2指向6了，遍历前面的数字，第一个数是2，二者相差4，那么在dp[2]的HashMap就可以建立 4->1 的映射，第二个数是4，二者相差2，那么先在dp[2]的HashMap建立 2->1 的映射，由于dp[1]的HashMap中也有差值为2的映射，2->1，那么说明此时至少有三个数字差值相同，即这里的 [2 4 6]，我们将dp[1]中的映射值加入结果res中，然后当前dp[2]中的映射值加上dp[1]中的映射值。这应该不难理解，比如当i=3指向数字8时，j=2指向数字6，那么二者差值为2，此时先在dp[3]建立 2->1 的映射，由于dp[2]中有 2->2 的映射，那么加上数字8其实新增了两个等差数列 [2,4,6,8] 和 [4,6,8]，所以结果res加上的值就是 dp[j][diff]，即2，并且 dp[i][diff] 也需要加上这个值，才能使得 dp[3] 中的映射变为 2->3 ，后面数字10的处理情况也相同，这里就不多赘述了，最终的各个位置的映射关系如下所示：

2     4     6     8     10    
     2->1  4->1  6->1  8->1
           2->2  4->1  6->1 
                 2->3  4->2
                       2->4

Quick explanation:

res is the final count of all valid arithmetic subsequence slices; map will store the intermediate results T(i, d), with i indexed into the array and d as the key of the corresponding HashMap.
For each index i, we find the total number of "generalized" arithmetic subsequence slices ending at it with all possible differences. This is done by attaching A[i] to all slices of T(j, d) with j less than i.
Within the inner loop, we first use a long variable diff to filter out invalid cases, then get the counts of all valid slices (with element >= 3) as c2 and add it to the final count. At last we update the count of all "generalized" slices for T(i, d) by adding the three parts together: the original value of T(i, d), which is c1 here, the counts from T(j, d), which is c2 and lastly the 1 count of the "two-element" slice (A[j], A[i]).

简单来说，map[i]存储的是以A[i]结尾的等差数列的个数，map[i].get(d)是以A[i]结尾，数字差值为d的等差数列的个数。对于j<i，使用map[j].getOrDefault(d, 0)，取出以A[j]结尾，差值为d的等差数列个数，在这些数列后添加A[i]就是符合条件差值为d的新数列。注意在更新map[i]时，要将[A[j],A[i]]这个长度为2的新数列考虑进去。

参考链接：该题很详细的英文逻辑思考过程，一定要看，能学到很多推理的关键思想

由第45题（472）所得的感想

As a rule of thumb, when there is difficulty relating original problem to its subproblems, it usually indicates something goes wrong with your formulation for the original problem.即当我们预先设立的dp数组定义无法设计出递推关系时，说明定义并不合适，此时可以增加维数（以包含更多的hidden information以帮助推理），或者改变dp数组的定义(此时可能在维数增加的情况下)，必要时也需要使用高级的数据结构如HashMap来节省空间。

46.（629:Hard）（非常经典题）K Inverse Pairs Array dp[n][k] denotes the number of arrays that have k inverse pairs for array composed of 1 to n

we can establish the recursive relationship between dp[n][k] and dp[n-1][i]:

if we put n as the last number then all the k inverse pair should come from the first n-1 numbers

if we put n as the second last number then there's 1 inverse pair involves n so the rest k-1 comes from the first n-1 numbers

...

if we put n as the first number then there's n-1 inverse pairs involve n so the rest k-(n-1) comes from the first n-1 numbers

dp[n][k] = dp[n-1][k]+dp[n-1][k-1]+dp[n-1][k-2]+...+dp[n-1][k+1-n+1]+dp[n-1][k-n+1]

It's possible that some where in the right hand side the second array index become negative, since we cannot generate negative inverse pairs we just treat them as 0, but still leave the item there as a place holder.

dp[n][k] = dp[n-1][k]+dp[n-1][k-1]+dp[n-1][k-2]+...+dp[n-1][k+1-n+1]+dp[n-1][k-n+1]

dp[n][k+1] = dp[n-1][k+1]+dp[n-1][k]+dp[n-1][k-1]+dp[n-1][k-2]+...+dp[n-1][k+1-n+1]

so by deducting the first line from the second line, we have

dp[n][k+1] = dp[n][k]+dp[n-1][k+1]-dp[n-1][k+1-n]

对于长度为n的数组，全逆序有(n-1)+(n-2)+.....+0总共n*(n-1)/2个inversed pairs。具体思路细节请参看代码实现及注释。

47.（466:Hard）（经典题）Count The Repetitions

直接Brute force即可得到答案，耗时1138ms。思路就是统计[s1,n1]能构成多少个s2，这个数字是count2，返回count2/n2即可。

How do we know "string s2 can be obtained from string s1"? Easy, use two pointers iterate through s2 and s1. If chars are equal, move both. Otherwise only move pointer1.
We repeat step 1 and go through s1 for n1 times and count how many times can we go through s2.
Answer to this problem is times go through s2 divide by n2.

48.（132:Hard）（非常非常经典题）Palindrome Partitioning II

这是一道非常非常经典的动态规划问题，该题难在需要两重的动态规划，一个动态规划用于判断子字符串i到j是否为回文，一个动态规划用于判断i到n-1要变成回文序列集至少要切多少刀。
为了说明思路，下面直接放上实现代码，请参看实现逻辑和代码备注：

    public int minCut(String s) {
	if(s == null || s.length() == 0) return 0;
        int n = s.length();
        boolean[][]  pal = new boolean[n][n]; //pal[i][j]表示字符i到j是否为回文序列
        int[] cut = new int[n];  //cut[i]表示，使s字符串i到n-1序列成为回文序列至少要切多少刀
        for(int i=n-1;i>=0;i--)  //从后往前遍历，因为递推过程中要用到i+1的状态
        {
            cut[i]=n-i-1; //假设i到n-1没有一个回文序列，则对于长度为n-i的序列，需要切n-i-1刀，使每个字符都成为单独的回文序列
            for(int j=i;j<n;j++) //j是从索引i往后遍历
            {
                if(s.charAt(i)==s.charAt(j) && (j-i<2 || pal[i+1][j-1]))//对于i,i+1,..,j-1,j，如果i到j长度为1或2，则一定为回文序列，否则还要保证i+1到j-1也是回文序列才行
                {
                   pal[i][j] = true; //i到j是回文序列
                   if(j==n-1)
                       cut[i] = 0;  //长度为1
                   else if(cut[j+1]+1<cut[i])
                       //注意此处是i不变，分割点j变，寻找最小的cut[i]
                       //对于更新cut[i]的过程：对于序列abcddc，显然cut[0]=2，在计算cut[1]时，j=1可得到最小答案使cut[1]=1;在计算cut[0]时，j=0可得到最小答案cut[0]=cut[1]+1=2
                       cut[i] = cut[j+1] + 1; //在j和j+1中间切一刀，分为"i到j"和"j到n-1"两部分
                }
            }
        }
        return cut[0];
    }

49.（188:Hard）（非常非常经典题）Best Time to Buy and Sell Stock IV

是Best Time to Buy and Sell Stock的第四类问题，限制交易次数，但总的思路也是分为该天"持有股票"或"不持有股票"两种情况。下面进行详细讲解：
最基本的思路：我们设立二维数组T，T[i][j]表示到第j天为止做了i次交易的最大收益，递推公式为T[i][j] = Math.max(T[i][j], Math.max(T[i][j-1], prices[j] - prices[m] + T[i-1][m]))。其中，T[i][j-1]表示第j天不作交易维持第j-1天的收益；prices[j] - prices[m] + T[i-1][m]表示到第m天只做了i-1次交易，第i次交易是在第m天买入，第j天卖出的，寻找使结果最大的m(0<=m<j)。该思路是最基本的思路，但却内存溢出，因为该思路的空间复杂度为O(kn)
优化思路：那么从上面的递推关系我们可以发现，对于T[i][j]的更新，我们只用到了相邻两维的数组信息，即第i维和第i-1维，所以我们可以使用滚动数组来优化空间复杂度。其次，上面的基本思路时间复杂度为O(n^3)，最内层循环主要耗费在m从0到j的遍历上，我们可以观察到：prices[j] - prices[m] + T[i-1][m]的j不变，i不变，只有m在变，所以将"- prices[m] + T[i-1][m]"看成一个整体maxDiff，每次更新它的值即可，保证它最大，便可以省去最内层的循环，而且他的实现思路不变。
具体的实现细节请参看代码实现备注及参考链接视频。
参考链接：印度小哥详细思路讲解

50.（140:Hard）（非常非常经典题）Word Break II

是Word Break I的升级版本，主要区别是：word break I是判断有没解，而word break II是给出所有解，但思路还是一样。
该题仍然使用top-down的带备忘录的DP解法，我们从左到右遍历字符串，一旦0到i子序列出现在字典wordDict中，则将i+1到n子序列进行更深层次的递归，向上返回当前处理字符串所能形成的sentence以进行句子的拼接。具体思路请参看代码注释和参考视频。
参考链接：花花Top-down讲解

51.（174:Hard）（非常经典题）Dungeon Game

该题的思路主要就是：从右下角逆向求解左上角的所需最小血量。设立二维数组hp，hp[y][x]表示在当前(x,y)坐标处出发，到达bottom right位置所需的最小血量，每一个单位初始化为Integer.max_value，因为我们要求最小血量，所以max_value不会影响我们的求解。之后在求解hp[i][j]时，我们需要从hp[i+1][j]和hp[i][j+1]中即下方和右方选取一个较小的值，使得hp[i][j]最小。考虑到当dungeon[i][j]无论大于小于0，时，从(i,j)到达(i+1,j)或(i,j+1)都只需要Math.min(hp[i+1][j], hp[i][j+1]) - dungeon[i][j]的血量值，当dungeon[i][j]>0，我们只需要少准备些血量；当dungeon[i][j]<0时，我们需要多准备些血量。
具体的思路细节参看代码实现及参考链接。
参考链接：花花中文讲解
We cannot determines the health without knowing how much health loss is waiting for us in the future. Thus we need to consider from the opposite way. i.e. from destination to start position.

52.（639:Hard）（非常非常经典题）Decode Ways II

是91题Decode Ways的升级版，该题和91题的解法一模一样，代码都能和91题的一样。
该题最好先以Top-down的思路先去理解，然后再以bottom-up的方式进行实现。top-down递归方式容易理解，bottom-up容易递推实现。
具体的思路请参看代码的详细注释及参考链接视频，一看就懂，叙述的话较为累赘。
参考链接：花花中文视频教程

53.（741:Hard）（非常经典题）Cherry Pickup

用两遍DP，先从左上角按取到最多樱桃数的路径走一遍，然后再从右下角按取到最多樱桃数的路径走一遍是不行的，这个思路相当于"贪心"。如下例所示:

左侧是grid，中间是dp思路，右侧是贪心思路
11100     |   111              0         |       111             0
00101     |     101            0         |         1             0
10100     |       0     +      101       |         1       +     1 
00100     |       0              1       |         1             0
00111     |       1              110     |         111           00000

如果按照贪心思想，最多只能取到10个，但是按DP思路可以取到11个。

所以要使用“DP思想”来进行求解，因为top-down的思路更为简单容易理解，下面以top-down进行讲解。因为题目描述是往返的一个过程，我们可以将其转化为从(n-1,n-1)坐标有两个人分别同时出发，只能往左或往上前进，求两者到达(0,0)时所能获得的最大樱桃数量。如果两个人同时到达一个位置，则该位置的樱桃只能被其中一个人捡到，此处默认是被第一个人捡到。而从当前位置(x,y)前进，两个人总共有4种可能的运动情况，即“左|左、左|上、上|左、上|上”。又因为两个人的运动步数是相同的，所以x1+y1=x2+y2，所以y2=x1+y1-x2，可降低一维的空间复杂度。
具体思路请参看代码实现及参考链接。
参考链接：花花中文讲解

54.（418:Medium）（非常经典题）Sentence Screen Fitting

该题用join函数用空格将sentence中word进行拼接，并在末尾也加上一个空格。使用一个变量start，代表新的一行第一个字符的起始位置，通过start%joinedSentence来定位当前行的结束位置，start/joinedSentence表示能展现几个完整的句子。

public int wordsTyping(String[] sentence, int rows, int cols) {
    String s = String.join(" ", sentence) + " "; //sentence=["a","bc","d"]，拼接为"a bc d "
    int start = 0, l = s.length();
    for (int i = 0; i < rows; i++) {
        start += cols;
        if (s.charAt(start % l) == ' ') {
            start++;  //当我们进行切割时，切割点刚好为' '时，可以将start加1，因为不同行的首尾相连的两个单词不必用' '分开 
        } else {
            while (start > 0 && s.charAt((start-1) % l) != ' ') { //当start-1指向的字符不是' '时，持续将start减小
                start--;
            }
        }
    }
        
    return start / s.length();
}

该题还能用动态规划的思路，下次复习时研究

55.（750:Medium）（经典题）Number Of Corner Rectangles

fix two rows (or two columns) first, then check column by column to find "1" on both rows. Say you find n pairs, then just pick any 2 of those to form an axis-aligned rectangle (calculating how many in total is just high school math, hint: combination).固定两行，按列扫描，然后任选其中两个pairs组成矩形

该题还能用动态规划的思路，下次复习时研究

56.（920:Hard）（非常经典题）Number of Music Playlists

该题使用DFS，递推公式为F(N,L,K) = F(N - 1, L - 1, K) * N + F(N, L - 1, K) * (N - K)，其中：

F(N - 1, L - 1, K)：If only N - 1 in the L - 1 first songs. We need to put the rest one at the end of music list. Any song can be this last song, so there are N possible combinations.

F(N, L - 1, K)：If already N in the L - 1 first songs. We can put any song at the end of music list, but it should be different from K last song. We have N - K choices.

Time Complexity: O((L-K)(N-K))

该递推公式将题目分为两种情况。第一种情况：前N-1首歌曲凑成L-1个听过的歌单，第N首歌曲可以加到任意一个歌单的最后。第二种情况：前N首歌曲凑成N-1个听过的歌单，因为总共要听L个歌曲，所以需保证添加的第L首歌曲在最后的[L-K,L-1]的范围内，不能与第L首歌曲重复。
对于base case的理解：

If N == L, every song is played at least once, then the result equals to the number of permutation of N music.

If N == K + 1, then we need to repeat the N first music, still the result equals to the number of permutation of N music.

the same songs must be K = N-1 songs apart, so the first N songs among L songs must be a permutation of N, so it's N!(N的阶乘). Since the same songs must be at least K = N-1 songs apart again, the next N songs must repeat exact orders of the first N songs, ... In other words, the first N songs determine the whole list. Hope this helps.

57.（363:Hard）（非常经典题）Max Sum of Rectangle No Larger Than K

先求以(0,0)、(p,q)为顶点的各个矩形面积，然后求该矩形内部小矩形的面积，可直接参看下面的代码，注释非常详细。

public int maxSumSubmatrix(int[][] matrix, int k) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return 0;
    int m = matrix.length, n = matrix[0].length, res = Integer.MIN_VALUE;
    int[][] sum = new int[m][n];	//存储以(0,0)、(p,q)为顶点的各个矩形面积
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            int t = matrix[i][j];	//求以(0,0)、(i,j)为顶点的矩形面积
            if (i > 0) t += sum[i - 1][j];
            if (j > 0) t += sum[i][j - 1];
            if (i > 0 && j > 0) t -= sum[i - 1][j - 1];	//减去重复的部分
            sum[i][j] = t;
            for (int r = 0; r <= i; ++r) {	//求以(0,0)、(i,j)为顶点的矩形内部的子矩形面积
                for (int c = 0; c <= j; ++c) {
                    int d = sum[i][j];
                    if (r > 0) d -= sum[r - 1][j];
                    if (c > 0) d -= sum[i][c - 1];
                    if (r > 0 && c > 0) d += sum[r - 1][c - 1];	//加上多减去的部分
                    if (d <= k) res = Math.max(res, d);	//更新res结果变量
                }
            }
        }
    }
    return res;
}

58.（935:Medium）（非常经典题）Knight Dialer

The problem can be transformed into: Traverse a directed graph (each node with a number as label and edges are defined by Knight's moving rule)

Start from 0 to 9 (因为可以从任意数字键开始)

Move N - 1 step

Return how many ways to reach the end

Easy to come up with a DFS solution to start traversal from 0 to 9

In each recursion, move to one of the current node's neighbors and the remain step becomes N-1

Stop recursion when N == 0

Optimization:

Observe the recursive problem. The variances are:

Current Node
Remain Steps

Therefore, we can store these two variables as the memo to speed up DFS (then it's a Top Down DP)

具体思路请参考代码和注释

59.（1027:Medium）（非常经典题）Longest Arithmetic Sequence

该题是典型的DP问题，对某一索引j上的数字A[j]，计算A[j]与所有A[i],i<j的所有数字的差，并在此基础上更新以当前A[j]为尾，方差为A[j]-A[i]的等差数列的最大长度，代码如下：

public int longestArithSeqLength(int[] A) {
    int res = 2, n = A.length;
    HashMap<Integer, Integer>[] dp = new HashMap[n]; 
    for (int j = 0; j < A.length; j++) {
        dp[j] = new HashMap<>(); //key是等差，value是以该A[j]为尾的相同等差的数列的最大长度
        for (int i = 0; i < j; i++) {
            int d = A[j] - A[i];
            dp[j].put(d, dp[i].getOrDefault(d, 1) + 1);
            res = Math.max(res, dp[j].get(d)); //更新结果集
        }
    }
    return res;
}

60.（1048:Medium）（非常经典题）Longest String Chain

该题一看就是一个典型的DP问题。为了使用DP，我们在这里使用bottom-up的思路，首先根据word的长度将数组进行排序，然后遍历每一个单词，通过尝试删除每一个位置上的字母构成新单词，查看当前的单词是否为之前单词的successor，并维护一个max变量记录当前单词对应chain的最大长度，最后将其存入字典中。

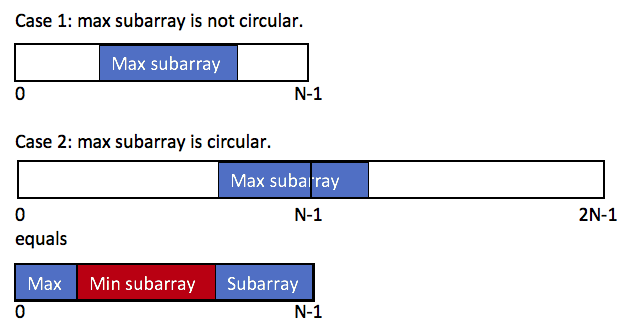
61.（918:Medium）（非常非常经典题）Maximum Sum Circular Subarray

So there are two case:

The first is that the subarray take only a middle part, and we know how to find the max subarray sum.
The second is that the subarray take a part of head array and a part of tail array. We can transfer this case to the first one. The maximum result equals to the total sum minus the minimum subarray sum.

Here is a diagram:

So the max subarray circular sum equals to max(the max subarray sum, the total sum - the min subarray sum).

Corner case: If all numbers are negative, maxSum = max(A) and minSum = sum(A). In this case, max(maxSum, total - minSum) = 0, which means the sum of an empty subarray. According to the deacription, We need to return the max(A), instead of sum of an empty subarray. So we return the maxSum to handle this corner case.

public int maxSubarraySumCircular(int[] A) {
    int total = 0, maxSum = -30000, curMax = 0, minSum = 30000, curMin = 0;
    for (int a : A) {
        curMax = Math.max(curMax + a, a); //以当前数字结尾和以当前数字开头的两种情况
        maxSum = Math.max(maxSum, curMax); //总的最大值
        curMin = Math.min(curMin + a, a); //以当前数字结尾和以当前数字开头的两种情况
        minSum = Math.min(minSum, curMin); //总的最小值
        total += a; //数组求和
    }
    //若数组中全为负数，不能返回0，subarray不能为空
    return maxSum > 0 ? Math.max(maxSum, total - minSum) : maxSum; //当maxSum大于0时，说明数组中存在正数，否则说明数组中全为负数，返回最大的那个负数
}

62.（361:Medium）（非常经典题）Bomb Enemy

这道题相当于一个简单的炸弹人游戏，让我想起了小时候玩的红白机的炸弹人游戏，放一个炸弹，然后爆炸后会炸出个‘十’字，上下左右的东西都炸掉了。这道题是个简化版，字母E代表敌人，W代表墙壁，这里说明了炸弹无法炸穿墙壁。数字0表示可以放炸弹的位置，让我们找出一个放炸弹的位置可以炸死最多的敌人。那么我这里的**方法是建立四个累加数组left, right, up, down，其中left是水平方向从左到右的累加数组，right是水平方向从右到左的累加数组，up是竖直方向从上到下的累加数组，down是竖直方向从下到上的累加数组，**我们建立好这个累加数组后，对于任意位置(i, j)，其可以炸死的最多敌人数就是left[i][j] + right[i][j] + up[i][j] + down[i][j]，最后我们通过比较每个位置的累加和，就可以得到结果。

63.（837:Medium）（非常非常经典题）New 21 Game

这道题说的是有 [1, W] 范围内的牌，问我们当拿到不少于K点的时候就停止摸牌，最终点数能不超过的N点的概率。那么我们先来分析下，拿到 [1, W] 范围内的任意一张牌的概率是 1/W，因为是随机取的，所以拿到任意张牌的概率都是相等的。那么点数大于W的时候，概率怎么算呢，比如 W = 10, 我们拿到15点的概率是多少呢？这时候肯定不止拿一张牌了，那么我们分析最后一张牌，可以取1到 10，那么能拿到 15 点就有十种情况，之前共拿5点且最后一张拿10，之前共拿6点且最后一张拿9，之前拿共7点且最后一张拿8，...，之前共拿 14 点且最后一张拿1。那么拿 15 点的概率就是把这十种的概率都加起来。这道题给的假设是每次取牌都是等概率的，不管什么时候拿到 [1, 10] 内的任意张牌的概率都是十分之一，所以我们拿最后一张牌（每一张牌其实都是）的概率都是 1/W。由于是且的关系，所以是概率相乘，可以将 1/W 提取出来，那么对于拿到x点的概率就可以归纳出下面的等式：

P(x) = 1/W * (P(x-1) + P(x-2) + P(x-W))
       = 1/W * sumP(x-W, x-1)

这里的x是有范围限制的，必须在 [W, K] 之间，因为小于等于W的点数概率都是 1/W，而大于等于K的时候，就不会再拿牌了。

    // 注意：0 <= K <= N <= 10000
    public double new21Game(int N, int K, int W) {
        if (K == 0 || N >= K + W) return 1;
        // dp[i]: probability of get points i, dp[i] = sum(last W dp values) / W
        // Wsum = sum(last W dp values), a sliding window with size at most W
        double dp[] = new double[N + 1],  Wsum = 1, res = 0;
        dp[0] = 1;
        for (int i = 1; i <= N; ++i) {
            dp[i] = Wsum / W;
            if (i < K)
                Wsum += dp[i]; //当i小于K时，会继续draw，往窗口内继续加概率
            else
                res += dp[i]; //计算点数在K到N范围内的累计概率
            if (i - W >= 0) Wsum -= dp[i - W]; //维护一个固定的窗口，窗口大小上限为W
        }
        return res;
    }

64.（1024:Medium）（非常非常经典题）Video Stitching

该题可以用动态规划来解决，具体的动态转移方程请参看下边的图片

public int videoStitching(int[][] clips, int T) {
    // dp[i][j] := min clips to cover range [i, j]（其实是前n个clips最少覆盖[i,j]range的个数）
    int[][] dp = new int[T+1][T+1];
    for(int i = 0; i < dp.length; i++)
        Arrays.fill(dp[i], 101); //101代表当前interval是不能被现有的clip覆盖的,因为clip的最大个数为100
    for (int[] c : clips) {
        int s = c[0]; //当前clip的起点
        int e = c[1]; //当前clip的终点
        for (int l = 1; l <= T; ++l) { //从interval的长度为1开始算起
            for (int i = 0; i <= T - l; ++i) {
                int j = i + l;
                if (s > j || e < i) continue; //interval和clip完全不想交
                if (s <= i && e >= j) dp[i][j] = 1; //clip完全包含interval
                //注意程序在运行到这里时，clip和interval是一定相交的
                else if (e >= j) dp[i][j] = Math.min(dp[i][j], dp[i][s] + 1); //clip与interval的后半部分相交，前半部分需要依赖先前的计算结果
                else if (s <= i) dp[i][j] = Math.min(dp[i][j], dp[e][j] + 1); //clip与interval的前半部分相交，后半部分需要依赖先前的计算结果
                else dp[i][j] = Math.min(dp[i][j], dp[i][s] + 1 + dp[e][j]); //clip只占interval的中间部分，前后两端均需依赖之前的部分
            }
        }
    }
    return dp[0][T] == 101 ? -1 : dp[0][T];
}

65.（975:Hard）（非常非常经典题）Odd Even Jump

我们从后往前遍历数组，当从数组一个位置向高处跳时可以到达终点，当且仅当从该高处点向低处点跳跃时可以到达终点；相似的，当从数组一个位置向低处跳时可以到达终点，当且仅当从该低处点向高处点跳跃时可以到达终点。于是我们可以据此写出DP状态转移方程。首先参考下面的例子：

We need to jump higher and lower alternately to the end.

Take [5,1,3,4,2] as example.

If we start at 2,
we can jump either higher first or lower first to the end,
because we are already at the end.
higher(2) = true
lower(2) = true

If we start at 4,
we can't jump higher, higher(4) = false
we can jump lower to 2, lower(4) = higher(2) = true

If we start at 3,
we can jump higher to 4, higher(3) = lower(4) = true
we can jump lower to 2, lower(3) = higher(2) = true

If we start at 1,
we can jump higher to 2, higher(1) = lower(2) = true
we can't jump lower, lower(1) = false

If we start at 5,
we can't jump higher, higher(5) = false
we can jump lower to 4, lower(5) = higher(4) = false

参考的具体代码思路及注释如下：

public int oddEvenJumps(int[] A) {
    int n  = A.length, res = 1;
    boolean[] higher = new boolean[n], lower = new boolean[n];
    higher[n - 1] = lower[n - 1] = true; //我们从后往前遍历数组
    TreeMap<Integer, Integer> map = new TreeMap<>(); //map存储数组元素的值及其对应的下标索引
    map.put(A[n - 1], n - 1);
    //因为我们从后向前遍历索引，所以map中存储的都是当前遍历位置之后的key，所以通过ceiling key或floor key取到的元素值肯定
    //都是在当前元素索引之后的值，恰好与题目要求吻合
    for (int i = n - 2; i >= 0; --i) {
        Map.Entry hi = map.ceilingEntry(A[i]), lo = map.floorEntry(A[i]);
        //当从数组一个位置向高处跳时可以到达终点，当且仅当从该高处点向低处点跳跃时可以到达终点
        if (hi != null) higher[i] = lower[(int)hi.getValue()];
        //当从数组一个位置向低处跳时可以到达终点，当且仅当从该低处点向高处点跳跃时可以到达终点
        if (lo != null) lower[i] = higher[(int)lo.getValue()];
        //如果该位置是起始点，当且仅当从该位置向高处跳时才能算作一个valid的位置，因为第一跳肯定是odd jump
        if (higher[i]) res++;
        //更新当前的map，需要注意的一点是，这里如果A[i]之前出现过，map会存储较小的索引(覆盖)，与题目要求恰好一致
        map.put(A[i], i);
    }
    return res;
}

66.（818:Hard）（非常非常经典题）Race Car

该题在自己的实现方式中采用的是BFS，较易理解且更容易上手，但标准解法可能是使用DP。
BFS解法的核心思想是，我们将position/speed作为每一步的状态，从每一个状态开始，分别执行A和R操作，并查看更新后的状态，如果新状态之前没有出现过，且新状态的位置更没有比一开始起始位置和target位置的距离还远(剪枝)，则存储新状态。

    class CarInfo{
        int pos, speed;
        public CarInfo(int p, int s) {
            pos = p;
            speed = s;
        }
    }
    public int racecar(int target) {
        Set<String> visited = new HashSet<>();
        String begin = 0 + "/" + 1; // 每一步的状态是 position/speed
        visited.add(begin);
        Queue<CarInfo> queue = new LinkedList<>();
        queue.add(new CarInfo(0,1));
        int level = 0; // level代表最短的步数
        while (!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                CarInfo cur = queue.poll();
                if (cur.pos == target) return level;
                String s1 = (cur.pos + cur.speed) + "/" + (cur.speed * 2); //从当前位置执行A操作后的下一状态
                String s2 = cur.pos + "/" + (cur.speed > 0 ? -1 : 1); //从当前位置执行R操作后的下一状态
                //注意，这里除了进行visited判断以外，还涉及剪枝，新状态到target的距离必须得比起始位置到target位置的距离短
                if (Math.abs(cur.pos + cur.speed - target) < target && !visited.contains(s1)) {
                    visited.add(s1);
                    queue.add(new CarInfo(cur.pos + cur.speed, cur.speed * 2));
                }
                if (Math.abs(cur.pos - target) < target && !visited.contains(s2)) {
                    visited.add(s2);
                    queue.add(new CarInfo(cur.pos, cur.speed > 0 ? -1 : 1));
                }
            }

            level++;
        }
        return -1; //-1代表不可能到达target的位置
    }

DP的解法等下次复习有空的时候再学习理解

67.（1143:Medium）（非常经典题）Longest Common Subsequence

很经典常见的dp形式

public int longestCommonSubsequence(String text1, String text2) {
    int len1 = text1.length(), len2 = text2.length();
    int[][] dp = new int[len1+1][len2+1];
        
    for(int i = 0; i < len1; i++){
        for(int j = 0; j < len2; j++){
            if(text1.charAt(i) == text2.charAt(j))
                dp[i+1][j+1] = dp[i][j] + 1;
            else
                dp[i+1][j+1] = Math.max(dp[i+1][j], dp[i][j+1]);
        }
    }
        
    return dp[len1][len2];
}

68.（1155:Medium）（非常经典题）Number of Dice Rolls With Target Sum

利用DP，根据紧挨的上一个状态来计算当前状态

public int numRollsToTarget(int d, int f, int target) {
    int MOD = 1000000007;
    int[][] dp = new int[d + 1][target + 1]; //dp[i][j]:使用i个骰子，使所有骰子和为j的可能性个数
    dp[0][0] = 1;
    //how many possibility can i dices sum up to j;
    for(int i = 1; i <= d; i++) {
        for(int j = 1; j<= target; j++) {
            if(j > i * f) {
                continue;         //If j is larger than largest possible sum of i dices, there is no possible ways.
            } else {                      //watch out below condition, or NPE
                for(int k = 1; k <= f && k <= j ; k++) { //我们看的相当于是第i个骰子的点数，点数从1到f都可能
                    dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % MOD;
                }
            }
        }
    }
    return dp[d][target];
}