Array (Python Java) - ShuweiLeung/Thinking GitHub Wiki

至2018.4.2，未做题目：Leetcode Array 126题、782题(有笔记)

数组问题，需特别注意：“数组能否为空”、“数组的长度”“是否需要单独处理开头、末尾元素”等其他特殊情况是否存在！

1.（766:easy）Toeplitz Matrix

• 输入矩阵（m行，n列），转换为列表形式，用len函数分别计算列表的长度（即m）和列表第一项的长度（即n）。
• 第一行需要进行测试所有的元素，即n个元素，依次进行行列值加1进行计算比较，之后从第二行开始只需测试每行的第一个元素。
• 如下图矩阵所示，其中的数字表示“序号”。程序第一行需检查1->6->11>16, 2->7->12, 3->8, 4 这四个元素(n)，从第二行开始，只需一次检查5->10->15, 9->14, 13即可

 1  2  3  4
 5  6  7  8
 9  10 11 12
 13 14 15 16

2.（747:easy）Largest Number At Least Twice of Others

• 该题目乍一看需要让每一个元素和最大元素做比较，其实只要将输入的数组进行从大到小排序，然后将最大元素和次大元素作比较，若满足大于等于2倍的条件，则其他元素均满足。排序算法可以利用Python内置的方法。
• 进行排序时，注意将原列表进行保存，以返回最大元素在列表中的原有位置。

3.（746:easy）（经典题）Min Cost Climbing Stairs

该题目属于动态规划问题，需搞清楚动态规划、递归、搜索、贪心算法之间的区别与联系

• 依据题意，开始的第一步可以从cost[0]或cost[1]开始，每次可以选择跨越一个台阶或者两个台阶直至到达the top of the floor。我们可以理解为初始状态从cost[-1]开始，且cost[-1]=0,走一步则到达cost[0]，走两步则到达cost[1]。更具体的来讲，对于一个5级台阶，初始状态在0级台阶，则最终状态为6，只是cost[0]=cost[6]=0。
• 基于以上理解，我们每往前走一个阶段，比较走一步和走两步所付出的代价，从中选取最优的策略，直到到达顶端。(这种从前往后的遍历穷举理解非常复杂，需要搜索所有的上升路线，非常耗时，不是正确解法，但可以从前往后进行实现（见实现代码）)
• 正确的思路为：从后往前进行考虑，若要到达6状态，我们可以从5走一步到6（即5->6），或从4走两步到6（即4->6）。假设我们已知从0到4的代价x与从0到5的代价y，则最小代价只需选择x和y中的较小值。对从0到4和从0到5的代价以此类推。

官方Hints:
Say f[i] is the final cost to climb to the top from step i. Then f[i] = cost[i] + min(f[i+1], f[i+2]).

4.（724:easy）Find Pivot Index

• 该题目类似于求中位数，但实则不同。因为数组中的数字可正可负，所以我们不能以某些数列的和大于或小于整个数组的和的一半作为循环判断结束的条件。

 例如：
 nums = [4, 9, -11, -3, 2]
 整个数组的和为1，若将0.5作为循环遍历结束标志，则当4+9=13>0.5时，就应该退出循环，但实际的index应为3，4+9-11=2。

• 解决办法：可以先将整个数组求和，设立一个指针从数组的左侧开始遍历求和，同时比较即将遍历的下一个数与剩下数列的和，若满足条件则返回对应的index索引，否则返回-1，遍历直到数组的末尾才结束。

一定要考虑边界特殊情况，如：数组为空（注意是否有non-empty非空限制）以及 返回的索引index = 0或数组的末尾位置

5.（717:easy）1-bit and 2-bit Characters

• 该问题中，2-bit Characters虽然有10与11之分，但个人认为并没有什么影响，只需把其看做长度为2的字符即可，而1-bit Characters自然为长度为1的字符。
• 因为2-bit字符一定以1开头，1-bit字符一定以0开头，所以从左往右遍历，我们按字符顺序来扫描整个数组，而不是以bit顺序来扫描。故遇到1-bit字符，下一个扫描位置为i+1；若遇到2-bit字符，下一个扫描位置为i+2.我们定义数组的长度为length，因数组索引从0开始，当i+1=length时，最后一个字符一定为1-bit；当i+2=length时，最后一个字符一定为2-bit。

6.（697:easy）Degree of an Array

• 该问题中，第一个子问题是求给定数组的degree值，第二个子问题是求有相同degree值的最小子序列长度。为了缩短运行时间Runtime，我们争取在求第一个子问题时，记录一些与第二个子问题有关的信息。
• 一种解法为：我们先用set()函数将列表转化为集合，得到整个数组中不同元素的种类。接着，我们从左到右遍历数组，建立一个字典，键为“元素种类”，值为该元素在数组中出现的位置列表。

  例如:
  nums = [1,2,2,3,1,4,2]
  我们建立如下形式的字典 dict = {'1':[0,4], '2':[1,2,6], '3':[3], '4':[5]}，于是output=元素2的列表首末位置之差加1.

7.（695:easy）（经典题）Max Area of Island

深度优先搜索：属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。即在搜索其余的链接结果之前必须先完整地搜索单独的一条链。

• 该问题代表一类大问题，使用的核心思想即是搜索，遍历所有可能路径，我们在此假设搜索路径为：上->右->下->左。
• 注意：在图的搜索遍历过程中，将访问过的位置设为0，防止递归过程中的重复遍历。搜索就需要使用到递归，注意递归退出条件。

8.（674:easy）Longest Continuous Increasing Subsequence

• 该问题较简单，只需记录一个最长递增子序列长度和当前递增子序列长度两个变量，当遇到nums[i+1]<=nums[i]时，便更新最长递增子序列长度，并将当前递增子序列长度的值初始化为1，重复此操作直至将整个数组遍历结束
• 注意：“递增”必须是严格大于，小于等于都是不符合条件的

9.（665:easy）Non-decreasing Array

• 该题与674题类似，均是对连续的、上升的子序列做操作限制。
• 根据观察，修改至多一位保证整个数组是值上升的（大于等于），则其上升子序列（子序列互相之间不是严格上升的）的数量不能超过2。

   例如：
       nums = [3,4,6,2,7]       其有两个上升子序列[3,4,6]与[2,7]

• 因为此处的“上升”是指“大于等于”，为了修改一位而对之后的序列不产生上升顺序的影响，应将不满足条件的一位修改为该位置的前一位，即若nums[i]>nums[i+1]，以第i个元素作为参照系，将nums[i+1]修改为nums[i]。举例来说，应将上述例子中的2修改为6，而不是随意修改为一个大于6的数（如8），否则[8,7]仍为下降的。
• 同样的，另一种同时需要考虑的情况是：若nums[i]>nums[i+1]，以第i+1个元素作为参照系，将nums[i]修改为nums[i+1]。在上述例子中，也就是将6修改为2。
• 在将上述两种最基本的情况考虑在内后，我们做出的每一次修改，都不能破坏之后序列的上升性（第一种情况）或之前序列的上升性（第二种情况）。举例来说，nums = [3,4,6,2,3],若将2修改为6，则破坏了[2,3]的上升性；若将6修改为2，则破坏了[3,4,6]的上升性。

更简单的方法见代码实现的注释部分！

• 清晰的理解思路：（贪心Greedy）This problem is like a greedy problem. When you find nums[i-1] > nums[i] for some i, you will prefer to change nums[i-1]'s value, since a larger nums[i] will give you more risks that you get inversion errors after position i（将nums[i]增大可能会影响后面的升序关系，所以先尽量降低nums[i-1]，在迫不得已的情况下，即nums[i]比nums[i-2]还小的情况下，才增大nums[i]）. But, if you also find nums[i-2] > nums[i], then you have to change nums[i]'s value instead, or else you need to change both of nums[i-2]'s and nums[i-1]'s values.

10.（661:easy）Image Smoother

• 该题在实现时需要复制一个相同的matrix作为运算的参照，原matrix用于修改。
• 在实现时，只需注意特殊位置与普通位置的区别即可。尽量将特殊位置一般化，无论对什么位置都运行相同的判断过程，简化运算的复杂度。

11.（643:easy）Maximum Average Subarray I

• 该题较简单，只需循环截取长度为k的子序列并比较其总和即可

12.（628:easy）Maximum Product of Three Numbers

• 该题乍一看，分析起来非常复杂，实则按分类讨论思想，问题会变得非常简单。因为题目已经限定了因子的数量为3，所以为了求得最大值，共有以下几种情况。
• 第一种情况：“正正正”，自然要取排序后的最大的三个数。第二种情况：“正负负”，取排序后的一个最大数字与两个最小数字，因为有的数组中不存在负数，该情况下是指最大正数与两个最小正数。第三种情况：“负负负”，该情况是指数组中数字均小于0的情况，取排序后的最大的三个数，可以与第一种情况进行合并。
• 基于以上分析，每次我们只需比较第一种情况与第二种情况下两种取法的乘积大小，返回较大值即可。

涉及“大小”的问题往往需要进行排序处理

13.（605:easy）（经典题）Can Place Flowers

• 刚开始拿到题目的时候，就想通过对比花圃可栽种的最大花朵数与输入的期望栽种花朵数作比较，从而判断是否满足条件。于是通过最笨拙的推理归纳，总结出0在不同位置不同数量下对应的规律，从而实现了一个时间复杂度非常高的解法。

• 之后发现，如果模拟肉眼扫描判断的过程，先不考虑能否全部种完，而是在遵照堪培拉规则的前提下，从最开始尽可能多的种植花朵，最后在扫描完整个花圃后，检查是否还有剩余的花朵没有种出，若剩余的花朵数为0则刚好种完，若为负数则花圃还能种更多的花朵。于是在第二种想法的驱动下，我们将开头为0或末尾为0的情况考虑进去，通过控制当flowerbed[i]=1时对指针的跳跃处理，尽可能保证每次将遍历的指针i指向最可能种植的位置，即在flowerbed[i-1]一定为0的前提下，只需判断flowerbed[i]和flowerbed[i+1]是否为0（开头末尾0的情况另外考虑）。

• 第二种思想在实现过程中，没有对原花圃数组进行修改，主要的难度是在控制指针i的“精准跳跃”上，需要考虑若遇到连续多个1时，通过while循环跳跃掉连续1串，直到第一个潜在的可能满足条件的0位置。而根据官方的解题思路，我们可以分别遍历每一个位置而不做任何指针的跳跃，分别判断i-1，i，i+1位置是否均为0，若成立则将i位置修改为1。

• 记得分析问题时要考虑特殊情况

• 若不想特殊处理首末位置，也可以在运算前人为的在首末位置前后各增加一个0

• 注意:连续的两个并列if判断语句，在执行完第一个if语句后仍会执行第二个if语句的判断条件，此时可能会发生“指针越界”的问题。

    例如:    nums = [0,1,0]
            while(i < len(nums)):
                if(nums[i] == 0):
                     i += 1
                if(nums[i] == 1):
                     print("Errors may happen!")
                     i += 1`
    本意是while循环中，两个if语句只执行其一，但实际上两个if语句的判断条件每次都会执行。当i=2时，第一个if语句会将i加1，本意想在
    下一次执行while循环判定的时候自动退出，但因为两个if语句是并列的，当第一个if语句执行完，会不可避免的运行第二个if语句的判断条
    件，从而发生数组下标的越界问题。

14.（35:easy）Search Insert Position

• 这个题非常简单，只需要使用python的内置函数判断target是否在数组中，若不存在则依次比较返回其应该所处的位置
• 注意：分析问题一定要全面！即数组中有比target大的数字，没有比target大的数字和该target在数组中，需把所有情况分析完整。

15.（66:easy）Plus One

• 要理解题意，将一个数组表示为一个数字，加一后还是用数组表示运算后的结果，并返回该数组。

16.（119:easy）Pascal's Triangle II（杨辉三角）

    杨辉三角有两条重要的性质：
    1.第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
    2.除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和
    （也就是说，第n行第k个数字等于第n-1行的第k-1个数字与第k个数字的和）。这是因为有组合恒等式：
    C(n,m)=C(n-1,m-1)+C(n-1,m)，即每个数等于它上方两数之和。可用此性质写出“整个”杨辉三角形。

• 对利用第一种性质的解法来说，需要实现排列组合函数功能。直观上，很显然用第一个性质来实现非常简单，但OJ判定为“超时”，所以我们只能用第二个性质进行实现。
• 利用第二个性质，我们首先初始化一个只有三层的杨辉三角，即rowIndexRange=0~2。当输入的rowIndex大于2时，我们利用“每个数等于它上方两数之和”的性质计算接下来的所有层，直至rowIndex层，然后将该层返回。额外的空间复杂度应为O(n)，时间复杂度更小。虽然该实现方法感觉较第一种更复杂，需要逐层推理，但实际上更有效。

17.（167:easy）Two Sum II - Input array is sorted

• 注意题目说了两个重要条件：1.有序数组 2.有唯一解。所以解的两个数一定都是数组中唯一存在的数。
• 是已经排序好的数组，从头开始遍历，然后检查target-nums[i]是否在给定数组中，有则返回下标，否则继续扫描。
• 这里使用index方法返回下标索引会被判定为超时，所以这提醒我们要使用时间复杂度更低的搜索算法（如二分查找）。另一种解题思路为（双指针解法）：设立双指针分别指向数组的头和尾，然后头指针从前往后扫描，尾指针从后往前扫描，若指针指向的两个数字和小于target，因尾指针指向最大值，故向右移动头指针；若小于target，缩小和值，向左移动尾指针。

18.（189:easy）Rotate Array

• 该题较简单，最简单的方法只需要利用pop方法删除并返回数组的最后一个元素，然后再将该元素insert至数组的首位即可。这是对数组元素进行单个的操作。
• 另一种耗时更短的操作是利用切片，将后k个和剩余的片段利用切片操作取出，将原数组进行片段的重新排列，即nums[:] = nums[-k:]+nums[0:-k]。注意：左侧nums后面必须跟上[:]，否则nums表示一个新的局部标签变量，并不是指传进来的参数nums。
• 注意考虑当移动位数“k > len(nums)”时，要取k%len(nums)的余数

19.（283:easy）Move Zeroes

• 一个关键的点需要注意，当删除数组中的元素时，原来各数组元素的下标会发生变化，所以需要先遍历一遍数组记录各个0的位置，然后依次删除0，而每删除一个0，剩余0的下标索引需要减1。应对该问题最好使用while循环而不是使用for循环，在删除后不要i+1，而是当没有删除元素时（不满足条件时）才进行i+1的操作，从而保证每个元素都被遍历到。

    例如：       nums = [0,0,1]
                for i, val in enumerate(nums):
                    if(val == 0):
                         positions.pop(i)
                当i=0时删除了0位置上的0，此时原来第二个位置的0变到了第一个位置，它的下标由1变为0，而下次遍历i=1，
                恰好跳过了对原来第二位置0的处理。

20.（27:easy）Remove Element

• 该题实际上和上题（283题）相近，可以用上题的方法来解决该题，但注意到“modifying the input array in-place with O(1) extra memory”，故不能利用额外的数组列表进行拷贝，于是采用如下的方法：（列表推导式）nums[:] = [i for i in nums if i != val]
• 使用列表推导式不用考虑在删除元素时带来的原来未删除元素数组下标变化可能带来的错误影响

21.（121:easy）（经典题）Best Time to Buy and Sell Stock

• 我们在思考此题时因分为两种情况，即存在买入卖出最大正差值的情况和若买入卖出时收益必为0或者负数的情况，后者只需将输入数组与降序排序后的输入数组进行比较即可解决，而前者较为复杂。
• 对第一种情况，一种非常简单的暴力解法，是设置两个while循环，在O(n^2)的时间复杂度下，计算出每一个买入和卖出的价格差值并取最大收益，但OJ会将此判定为超时
• 另一种方法：动态规划法。从前向后遍历数组，记录当前出现过的最低价格，作为买入价格，并计算在当前买入价格的情况下，当天出售获得的最大收益，作为可能的最大收益，整个遍历过程中，出现过的最大收益就是所求结果（局部最优->全局最优)。

需要搞清楚什么是“动态规划”及其原理

22.（26:easy）Remove Duplicates from Sorted Array

• 题目的关键是Sorted，给出的数组是排好序的，所以处理起来较简单，不需要每删除一种元素就遍历一遍数组，可以在一次扫描过程中完成题目规定的操作。
• 因为涉及到数组元素的删除，如19题（Code283题）笔记所示，每删除一个元素后，原来各元素的索引下标会发生变化（减1）。解决办法是：使用while循环而不是使用for循环，在删除后不要进行i+1操作，而是当没有删除元素时（不满足条件时）才进行i+1的操作，从而保证每个元素都被遍历到。
• 根据该题，我们发现列表(list)的remove(val)操作必然会扫描一遍数组找出第一个与val相同的元素并将其删除，而pop(i)操作会直接删除索引i位置上的元素并不进行数组的遍历，从而得出以下结论：pop()删除元素的效率远高于remove()。

23.（88:easy）Merge Sorted Array

• 该题实现起来较为简单，只是有一些小的细节需要注意，因为在Judge时，测试用例会对这些细节的特殊情况进行测试。
• 第一个注意点：传入的m值（nums1的实际长度）与len(nums1)可能不相同，因为nums1的长度可能为m+n，所以nums1=[1,2,3,0,0]，末尾填充0以确保nums2有位置可以插入，因而在程序的开始就要更新nums1，将其多余的0都全部删掉（python下列表长度可变）。
• 第二个注意点：在遍历依次比较nums1和nums2两个数组中的元素时，注意指向nums1、nums2的指针p、q不要越界，每次循环均需判断指针的位置。
• 第三个注意点：当p<m而q=n时，可以直接返回；当p=m而q<n时，将nums2剩余的元素全部都插入nums1的末尾。

24.（268:easy）（经典题）Missing Number

• 该问题有多种方法，每种方法的效率有所不同
• 方法一：先将输入的数组进行排序，然后从左到右一次遍历比较相邻的元素值是否相差1，若相差1则继续，否则返回缺少的元素。该方法在解决时需要注意每个数组的起始位置应该均为0，最大数字应为数组的长度值。
• 第二种方法：利用数字的可加和性质（一个数学技巧）。已知数组的最大元素应为数组长度的值，将0到数组长度值之间的数字进行加和，与数组中原有元素的和进行作差运算，结果即是答案。

25.（118:easy）Pascal's Triangle

• 该问题与16题(119)解法基本一样，同样是模拟递推公式（C(n,m)=C(n-1,m-1)+C(n-1,m)，即每个数等于它上方两数之和），可以在最短的时间内得出运算结果。

26.（53:easy）（经典题）Maximum Subarray

• 该题需要学习一个新的算法：Kadane Algorithm，时间复杂度为O(n)。
• O(n)方法（Kadane算法的改进，动态规划解法）：遍历array，对于每一个数字，我们判断，（之前的sum + 这个数字） 和 （这个数字） 比大小，如果（这个数字）自己就比 （之前的sum + 这个数字） 大的话，那么说明不需要再继续加了，直接从这个数字，开始继续，因为它自己已经比之前的sum都大了。反过来，如果 （之前的sum + 这个数字）大于 （这个数字）就继续加下去。这个方法和Kadane Algorithm 差不多， Kadane 的算法是，如果之前的sum 小于0了，就重新计算sum，如果sum不小于0，那么继续加。
• 另外一种方法O(n)复杂度:divide and conquer approach,分治思想。我在这里并没有搞懂他的实际含义，需要之后再次理解，分治思路的解法思想请参考该链接：分治思想解决最大子数组问题
• 当然，该题最简单的方法自然是暴力解法，算出每一个可能长度可能子序列的和并取其中的最大值，但被OJ判定为超时

27.（122:easy）（经典题）Best Time to Buy and Sell Stock II

• 该题是21题（121）的变种，从只能一次买卖到可以多次进行买卖，本质上来讲，解决的方法基本相似，都是动态规划问题（局部最优->全局最优）
• 解决思路是：在某一买入价格下，我们每当遇到该买入价格可达到最大的卖出收益时卖出股票，并将相关变量清零。即，我们设立一个maxProfit存储某买入价格对应的可能最大收益，一旦某日的价格虽然比买入价格高但卖出收益不及之前已经求得的最大收益时，则在该日的前一日卖出，并将该日的价格作为一个新的买入价格；或者，当某日的价格比买入价格还低或者与买入价格相同，则在该日的前一日卖出，并将该日的价格作为一个新的买入价格。当然，我们上面讨论的都是理想情况，即某买入价格的maxProfit是大于0的，但也可能一旦某一天买入股票，注定在局部情况下（按上述描述的规则）卖出时是要赔本的，即某些买入价格对应的maxProfit<=0是恒成立的，这种情况下，我们在每次累加总收益时需要作判断，只有在maxProfit>0时才能卖出，否则应忽略该买入价格情况下的交易，形象的理解为：我们不在这一天买入该支股票。
• 网上还流传一个非常简单但不一定符合题意（单日只能买入或卖出）的解法：流传解法

28.（169:easy）Majority Element

• 该题较简单，只需原地将nums数组进行排序，然后从左往右一次遍历，记录每一个元素出现的次数，当遇到一个新元素时，比较之前的元素出现次数与 ⌊ n/2 ⌋ 的大小，若大于则直接返回旧元素，否则将计数器重置为1，从新元素开始重新计算。
• 注意：末尾元素需要在循环后特殊处理判断

29.（217:easy）Contains Duplicate

• 该问题与上题28题（169）解决方法类似，只是将函数的返回条件改为：若之前元素出现次数大于等于2，则返回True；若遍历完整个数组后没有一个元素的出现次数大于等于2，则返回False。
• 注意：末尾元素需要在循环后特殊处理判断。题目条件中没有说数组长度一定大于等于1，所以空数组也需要考虑。

30.（219:easy）（经典题）Contains Duplicate II

• 该题是上一题29题（217）的变种，在统计每个元素出现次数的基础上增加了一次比较操作，该操作的思想如下：
• 因为题目要求我们比较的是相同元素值的某两个位置之间绝对距离小于k，即进行比较操作的前提是：该元素的出现次数大于等于2，且可以进行比较的最大次数为该元素在数组中出现次数减1

    如：..2...2.2..2...
       2在数组中出现了4次，可能比较的最大次数为3。
       因为四个2有3个间隔，只能第一个与第二个比较，第二个与第三个比较，第三个与第四个比较。

• 基于上述前提，我们以之前的例子为例，详述进行多次比较的过程：我们首先求出在当前数组中第一个2与第二个2的索引index1与index2，假如第一个2与第二个2的绝对距离（index2-index1）大于k，则从第二个2之前进行截断，即截断后的数组中第一个2消失，新数组是以第二个2为首，此时，之前的index2变为0，按照此思路，我们在最坏情况下执行2次截断，3次比较。若3次比较后仍不满足条件，则比较判断函数(judge())返回False。
• 注意：末尾元素需要在循环后特殊处理判断。题目条件中没有说数组长度一定大于等于1，所以空数组也需要考虑。

31.（1:easy）（经典题）Two Sum

• 该题有两种方法，第一种方法非常暴力，依次遍历数组（外循环），对每一个元素，查找target-element是否在数组中（内循环），如果有则返回相应索引否则遍历，这种方法非常暴力，O(n^2)的时间复杂度，耗时长。
• 第二种是借用字典的巧妙方法，在O(n)时间复杂度内即可求出结果。思路是：在循环遍历数组前，建立一个空字典，里面用来存储的键值对为target-element的值:element元素位置。每次在扫描到一个元素时，我们判断该元素是否在字典中，即是否有与其配对的另外一个之前已经扫描到的元素，若有则返回相应索引，否则在字典中添加该元素的对应另一半值和该元素位置。这里用字典保存之前已扫描过程中获得的信息从而减少了时间复杂度。

32.（414:easy）Third Maximum Number

• 这种有关大小的问题有时可以借助set集合函数将问题简单化，从而可以在遍历集合时不会取到重复的数字。
• 一种方法是：先判断集合元素是否小于3，若小于则直接取最大元素返回；若大于3，则在遍历前三个数字时，初始化firstNum、secondNum、thirdNum三个变量用来存储整个数组中前三大的数字，然后从第四个数字开始，分别与这三个变量进行大小的比较，并将相应变量的值进行更新，遍历结束后返回thirdNum即可。
• 在python3中引入sys包，-sys.maxsize是系统最小值，sys.maxsize是系统最大值(python2是sys.maxint)

33.（448:easy）（经典题）Find All Numbers Disappeared in an Array

• 若采用非常简单的思路，将变量i依次取值1到n，判断是否在数组中，会被OJ判定为“超时”
• 因此，我们需要采用一个非常巧妙的方法来解决“乱序”和“重复”两个问题。题目中说道：1 ≤ a[i] ≤ n (n = size of array)，因此为了要将数组元素的每一个下表索引值取到，我们需作a[i]-1运算。于是设计出如下思路：对于每一个遍历到的element，我们访问索引为element-1位置的数并将其置为-|num[element-1]|，因此，凡是数组中存在的数，执行该操作后对应位置将变为负数。而遍历结束后仍为正数的位置，将其索引值+1即为数组中缺失的数。
• 该题运用了正负技巧，将数组值与数组下标进行了关联，并将正负性作为过滤条件。

34.（561:easy）（经典题）Array Partition I

• 该题较简单，经分析，配对分类只可能有:"正正""负负""正负"，三种情况。又因为要使得所有配对中较小数的和最大，应该保证一个配对里的较小数与较大数差距最小，即以排序后的相邻数对作为一个组合。
• 为了使所有min(a,b)的pair尽量大，假设a<b，应该使a尽量大，b尽量小，这样才不会浪费b的大小，所以应该先将数组排序，从小到大依次配对，如(1,2)/(3,4)/(5,6)....

35.（566:easy）Reshape the Matrix

• 该题其实就是循环遍历创建一个新嵌套列表的过程。假设原数组有m行、n列，重塑后的数组有r行、c列，若mn!=rc，则不满足重塑条件，直接返回原数组。否则则一次遍历原数组的每一行，按r行、c列的要求来进行数组的重新拼接。注意，原数组的一行在没有全部插入到重塑数组之前不要遍历原数组中的下一行。

36.（485:easy）Max Consecutive Ones

• 该题较简单，和寻找数组中的最大数类似，只需要维持一个currentLength变量存储当前扫描到的连续1的长度，当取到的元素是0时，则判断currentLength和maxLength的大小，若大于则更新最大长度的值，同时将currentLength置零（小于最大长度也需要清零）。
• 注意：同样在遍历完整个数组后，需要特殊处理末尾元素。

37.（581:easy）Shortest Unsorted Continuous Subarray

• 双指针问题：可能涉及到对有序数组的遍历，指针指向一头一尾，根据当前的情况与条件进行对比，两指针从外侧向内侧收缩，最终找到符合条件的答案。
• 该题利用排序后的数组与原数组作比较，从前往后找到第一个与有序数组中元素不同的位置作为答案的头，从后往前找到第一个与有序数组中元素不同的位置作为尾，头尾之间即为答案（注意原数组即为升序数组的特殊情况）。

38.（532:easy）（经典题）K-diff Pairs in an Array

• 该题可分为三种情况，k<0则直接返回0；k=0则寻找数组中的重复数字个数；k>0则相对复杂，接下来我们对该种情况做更深入的探讨。
• 因为题目要求组合中的数字不能重复出现，这就提示我们一定要用set()函数对数组进行去重的处理。在处理完后，我们有两种思路。
• 第一种思路（非常暴力直接）：将去重后的集合再用list（）函数强制转换为列表并进行升序排列，接下来我们只需要从左往右进行扫描，并判断当前的扫描值val+k是否在列表中，存在则将pairs的数量+1。（该方法虽通过OJ，但效率极其低下，约beats 2-3%）
• 第二种思路（利用集合的并操作）：我们利用set()函数和“集合推导式”得出val+k并且存在于数组nums中的数值集合，再将其与未处理的集合进行“并操作”，便得到可以进行配对（(a,a+k)目标集合是由a+k组成的）的目标集合，其长度即为答案。

39.（442:Medium）（经典题）Find All Duplicates in an Array

• 这个题同33题（448）非常类似，其中用到的关键技巧就是“如何将数组元素的值与数组下标索引联系起来”，也就是作a[i]-1运算。
• 在33题（448）中，我们遍历每一个元素，并将对应索引的值置为负数，从而最后一次遍历数组时凡与正元素索引下标按以下规则计算得来的数值均是未出现的值。那么基于此思路，我们在解决该问题时，便有了两种解决方法。
• 第一种方法（置负数法）：同样是在遍历数组时，将元素对应索引下标位置处的数值值为负数，但是，因为某些元素出现过两次，所以在置其为负数时，应先判断是否为负数，若是正数则将其置负；若为负数，说明该索引对应的数值第二次出现，应将该数值加入到函数返回的列表中。
• 第二种方法（加和数法）：因为题目中说道每个可能重复的数最多只会出现两次，所以用上述第一种方法可以解决该问题。但若要找出重复出现3次的数，重复出现4次的数，上述方法就不能解决，此时因使用“加和数法”。同样要利用索引和值的关系，只不过，为了消除“未出现的数”对数组中元素值的影响，我们将数组中元素对应索引位置的值+len(nums)。因此，出现过一次的数，其对应位置应+len(nums);出现过两次的数，其对应位置应+2len(nums)，而未出现的数，其对应位置的值不变。这样，在用列表推导式筛选重复出现的数时，凡是“元素值/2len(nums) > 1”的，其对应的“索引+1”即为重复数字。

40.（667:Medium）（经典题）Beautiful Arrangement II

• 该问题实质考察的是数组元素的移动性质规律，我们可以举一个例子说明该问题的本质解决方法。

    如：
      当n = 5时，返回的数组中有5个不同的元素，因此相邻元素两两比较，k最大为4，故k的最大值应只能取到n-1。
      当n = 5，k = 1时：returnedList = [1,2,3,4,5]
      当n = 5，k = 2时：我们要在k=1的基础上做一次元素的移动，使得k只能+1。我们发现，只有将5移动到4的前面k才能恰好+1，若移动到3之前，则k只能+2。
                       因此，returnedList = [1,2,3,5,4]
      当n = 5，k = 3时：我们通过上面的规律，在k=1的基础上+2，5只能放在1和2之间或2和3之间，为了之后处理的方便，我们将5应插在可能出现的最前面的位置，即1和2之间。
                       此时returnedList = [1,5,2,3,4]
      当n = 5，k = 4时：在k=3的基础上+1，为了保证只能+1（若n>>5，此时4有很多可插入位置），从k=2的规律看来，我们应将末尾两元素的位置进行对调，从而满足了条件。
                       此时returnedList = [1,5,2,4,3]

• 根据该例子，我们发现了这样的一个规律：对一个排好序的从1到n的数组，其初始的k'=1，当k-k'>=2时，我们应将末尾元素插入到数组最开始可能出现的位置p（p=1,3,5,7...），此时k'=k'+2；当k-k'=1时，应将末尾的两个元素对调，此时k'=k'+1。依照该规律移动元素，直到k=k'。

41.（495:Medium）Teemo Attacking

• 该题较简单，只需要一次比较数组中两元素的差值和输入的duration，若差值大于等于duration，则在总的sumDuration基础上+duration，否则应在sumDuration的基础上加两元素的差值。
• 注意：需特殊处理末尾元素！

42.（238:Medium）（经典题）Product of Array Except Self

• 该题设置的非常巧妙，也是一个用双指针方法解决的问题。
• 因为题目中要求返回的是不含自己本身值的其他元素因子的乘积，因此我们先初始化一个长度为len(nums)，各元素值为1的返回数组列表。整个解题的思路为：设置两个指针p、q指向数组的头和尾，分别代表“p指针左侧位置的各元素因子乘积”和“q指针右侧位置的各元素因子乘积”，而某一位置i的真正返回值应为p x q x returnedList[i]，应返回列表各值初始化为1来避免将nums[i]计算进去，所以returnedList[i]=1，故位置i真正返回的是p*q的值。而在计算returnedList[i]的时候，可能会先计算returnedList[i]=returnedList[i]*p，然后再计算returnedList[i]=returnedList[i]*q，两者因为p、q指针的位置问题因而是不同步的。(该思路只beat 20%+，所以应有更巧妙的方法)
• 注意：题目中要求Solve it without division and in O(n)，故不能上来先把所有数乘积算出来，然后再逐个除以每个元素，这种思路是不被允许的。

43.（565:Medium）（经典题）Array Nesting

• 该题在一开始进行解决的时候，采用暴力解法，想以任何元素为链的头进行搜索，并取其中最长链并返回最长链的长度，但暴力解法被OJ判为超时。
• 之后又期望将之前遍历过的集合信息都存储下来，用作之后判定“是否需要以该元素作为链的头进行遍历搜索”的依据，即利用之前遍历获得的信息过滤掉不需2次搜索的链元素，却仍然“超时”。
• 但在debug的过程中，发现集合及相关集合操作（in、not in、copy）根本对结果（最长链的长度）没有任何帮助，只会增加耗时。而且发现规律：题目中说道“S[i] = {A[i], A[A[i]], A[A[A[i]]], ... } ”，我们可以将其形象表示为“A[i]->A[A[i]]->A[A[A[i]]]->...”或"A->B->C->..."。但题目却要求返回最长的集合长度，说明这个链是有“尾”的，而这里的尾是指链的末尾元素又会回指到链头，整个链构成一个“环”，即"A->B->C->D->F(->A)"，所以一定不存在"A->B->C->..."且"E->B->C->..."的情况，因为一个尾结点不可能同时与两个头结点相连，即这条环链是“不会分叉的”。
• 基于以上推理，我们不需要专门新开辟一个空间存储已经遍历过的元素（开辟新空间用于存储必然会涉及到列表集合的操作,如：in、not in、extend、copy等），只需要将访问过的元素值设为负数（如-1，因为题目中说道原数组中的值均在[0,n-1]之间）。因而每次进行搜索前均需判断该元素正负与否，若未搜索过则用length变量记录该条链的长度，并与最大链长度作比较。
• 注意：负数作为已访问元素的标记在之前题目中多次用到，应学会该技巧。

44.（769:Medium）（非常经典题）Max Chunks To Make Sorted

• 本质：该题的每个元素均不同，分布于[0,arr.length-1]，即对长度为n的数组来说元素取值为[0,n-1]且各不相同，所以* 排列后的元素值应与其对应位置的下标索引相同，即sortedArr[i] = i。
• 基于以上发现，我们应该建立一个position列表存储每一个当前位置的数若放置到其正确排序后的位置需要移动的距离。如：arr=[1,2,0,3],position=[1,1,-2,0]。那么怎么判断最短的需要排序的子数组呢，我们发现position数组中，凡是需要当做一个整体进行排序的子数组均有如下特点[position[n]>0,...,(0),..,position[n+m]<0]，因为可能存在position[n+m-1]<0的情况，因此需要设立一个变量maxIdealPosition来存储可能移动到的“最右端”位置，同时用ifPlusMinus变量标记我们现在搜索的是一个子数组而不是一个数，在满足position[i]<0且i=maxIdealPosition且ifPlusMinus=1的条件下，我们可以确认这个最短的需要排序的子数组已经搜索完整了。当然在遍历过程中可能需要随时更新maxIdealPosition的值（如上面arr=[1,2,0,3]的例子所示），在找到最短的需要排序的子数组后将ifPlusMinus置0。
• 更简单的方法：仔细观察一些例子，可以发现断开为新块儿的地方都是当之前出现的最大值正好和当前位置坐标相等的地方，比如例子2中，当 i=1 时，之前最大的数字是1，所以可以断开。而在例子1中，当 i=4 时，才和之前出现过的最大数字4相等，此时断开也没啥意义了，因为后面已经没有数字了，所以还只是一个块儿。

45.（39:Medium）(非常经典题)Combination Sum

• 使用的方法：backtracking（回溯）。根据题意，我们无法判断满足条件的路径数组长度，所以无法设立确定的指针数量来一一尝试比较，这时，我们应想到DFS深度优先搜索的思路，利用指针回溯来尝试得到可能满足条件的路径。
• 因为题目中说道路径中可以有重复元素，所以在递归时下次传入的起始路径与当前已经搜索到的元素索引应该相同，即我们已扫描到candidates[i]，下次dfs递归遍历的起始点仍是位置i到len(candidates)-1。
• 这里的“回溯”是指，当我们根据A->B->C的路径搜索时，发现走到C的时候此路不通，则会返回到上一次函数B，从B搜索下一个元素D，即尝试有一条路径A->B->D->....。而方法实现中，这个思想是用for循环来实现的 "for i in range(start=..., end=...):"。

46.（40:Medium）(非常经典题)Combination Sum II

• 该题与45题（39）非常相似，只是要求不能重复使用数组中提供的某个元素，但如[1,1,2,3]这样的数组，两个1可以同时各用一次。
• 解决办法只需要将上题dfs搜索的索引起始位置修改为i+1，即不再搜索相同的元素。
• 此外，我们还可以在上题解决办法的基础上进行适当的改进。因为在主函数中我们一开始已经对candidates数组进行了排序，所以在dfs递归过程中，如果某个索引i上candidates[i]>target成立，则不必继续向下层搜索candidates[i+1,i+2,....]，因为这些元素一定比candidates[i]大，因而该层的dfs函数可以直接返回，中断这个路径的搜索。

47.（216:Medium）（非常经典题)Combination Sum III

• 该题又是以上两题45题（39）、46题（40）的变种。在46题的基础上，题目规定了递归搜索的层次数k，即我们成功返回的路径path长度应等于k，而candidates题目中隐含说明为candidates = [1,2,3,4,5,6,7,8,9],且搜索路径中各元素不重复使用。
• 将以上区别分析清楚后，我们只需要在dfs函数的参数中增加一个参数变量depth，而每往下递归搜索一层，我们就将depth减1。当搜索的路径的元素和为target时，我们同时还要求其长度为k（或深度depth已减为0），且没有在returedPath中出现，只有以上三个条件均满足时，才加入返回的路径列表中。

<48>.（714:Medium）（非常经典题）Best Time to Buy and Sell Stock with Transaction Fee

• 网上将这道题的解决方法（下面提到）归为动态规划问题，因为当前的结果要参照之前的结果，而且每一次的取值更新都是局部最优的。
• 所有股票买卖的问题，请参照该链接进行分析：股票买卖原问题及扩展问题分析
• 网上给出了这样的一个解题的思路，非常奇妙。在任何一天i，我们可以将其分为当前步持有股票的收益s0和当前持有股票的收益s1，而这两个变量的更新又是由前一天i-1的两个状态决定的。即s0应该取“前一天没有股票的收益”和“至i-1天以前我手里有一支股票（不用关心i-1天前是否也有过其他股票的买卖），在今天i我将该股票卖出的收益”的较大值。而s1的更新策略相似，即取“仍然持有i-1天股票的收益”和“在i-1天没有持有股票的情况下，在第i天买入一支股票的收益”中较大值。最后一天返回s0，因为我们肯定不会在最后一天再买入股票（因为没机会卖出），要么维持前一天没有股票的收益，要么选择将倒数第二天的股票在最后一天卖出。
• 以上思路较易理解，但有一点非常关键：为什么要设立两个状态s0、s1？这两个状态是有主次之分的吗还是有同样优先级的？个人理解：s0和s1代表“并列”的两个状态，区别可能只是在时序上的关系。在返回答案的时候，因为题目隐形限制了时序（没有股票），因而返回s0而不是s1。
• 该题是动态规划问题，没有完全搞懂，需继续琢磨，what's the relationship of s0 and s1 on day i?具体实现及注释请参看代码。
• 下面讲一个通俗易理解的方法：

Define dp array:
    hold[i] : The maximum profit of holding stock until day i;
    notHold[i] : The maximum profit of not hold stock until day i;

    dp transition function:
    For day i, we have two situations:

        Hold stock:
        (1) We do nothing on day i: hold[i - 1];
        (2) We buy stock on day i: notHold[i - 1] - prices[i];

        Not hold stock:
        (1) We do nothing on day i: notHold[i - 1];
        (2) We sell stock on day i: hold[i - 1] + prices[i] - fee;

49.（78:Medium）Subsets

• 该题与47题（216）很像，同样是使用“回溯”的思想，使用深度搜索算法(dfs)，将可能的所有值都罗列出来。
• 唯一需要注意的是，我们在往subsets的返回列表中添加新集合时需要判断该集合是否已存在，此外我们应在dfs函数的参数中设置一个depth的深度参数，来限定搜索的最大深度，而该深度的初始值为len(nums)。

<50>.（287:Medium）（非常经典题）Find the Duplicate Number

• 该题是Leetcode 142.Linked List Cycle II（属于链表类topic）Linked List Cycle II的扩展，在这里我们先对该题进行解释说明。

      题目:Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
           Note: Do not modify the linked list.

• 解题思路为：我们设置两个指针（双指针法）,慢指针一次走一步，快指针一次走两步。假设从链表的某个结点开始进入环，两个指针一定会在环上相遇（类似于追及问题，环的长度是奇是偶对此没有影响，相遇是必然的，可以举例看出），此时，假设慢指针已经走了k步，则快指针则走了2k步，又假设环若存在，环的周长应用r来表示，这样有关系：2k-k=nr即k=nr(1)(n是快指针比慢指针多走了n圈)。那么现在，我们设从头结点到环的进入结点间的距离为s，从环的进入节点到两指针相遇的结点距离为m(可能慢指针也在环里走了大于1圈的长度才被快指针追上但在此对m的假设没有影响)，而由之前的假设我们得到，从头结点到两指针相遇的结点间距离为k(也是慢指针走过的距离)。于是我们可以将(1)式代入推理得出s=k-m=nr-m(2)。我们用图来形象的表示(由黑色箭头方向进入环，在环内按红色箭头方向前进)：

• 这样，我们利用快慢指针步长的不同找到了第一次相遇时，各个位置距离参数间的关系，接下来我们需要找到环的起始结点O的值。我们根据(2)式，若一个指针p1从相遇位置x开始前进，另一个指针p2从头结点开始前进，若两个指针一次都只走一步，一定会在结点O相遇，此时p1指针走了n-1圈加上快慢指针相遇时未走完的剩余的一圈距离，p2指针则恰好走了s的距离。换句话说，在第一次相遇后，我们将快指针的位置初始至头结点并将其步伐降为1，当两个指针再次相遇时，指针的值即为答案。其实，了解原理后，我们发现以上假设中给出的距离k、2k、s、r、m对结果不造成任何影响，只是方便推理理解而已。
• 以上花费如此多的篇幅来讲解Leetcode 142题，是因为该题可以看作142题的扩展。同样类比142题，我们将数组中每一个元素看做一个链表结点，每个元素的索引代表链表结点的值，每个元素的值代表指向下一个结点的指针索引。基于此，数组中重复元素均指向相同的结点（和上图指向O的箭头方向一致），被指向结点的值即为答案(即nums[x]的x)，只有这样，环的入口结点值才能为重复元素的值。而因为每一个元素均是[1,n]的，所以下标为0的数组元素一定不在环内，因为数组元素的值是不可能取到0从而返回到数组的头位置，这样下标为0的元素可以看作链表的头结点。
• 另外一个需要注意的点是，按如上规则定义的链表，一个数组可能会形成很多的环，但该题精妙之处在与，只要从数组下表索引为0的元素开始访问该链表，下标索引为0的元素nums[0]一定是有重复元素的环的入口。举一个简单的例子即没有重复元素的环只有一个元素，用反证法：假设nums[0]指向的是一个没有重复元素的环成立，则说明nums[nums[0]]一定是唯一的，因为nums[nums[0]]要形成环，则必须满足nums[nums[0]]=nums[0]，即其值一定要与下标索引相同，但nums[0]同样是数组0位置索引处的元素值，此时与假设矛盾，nums[nums[0]]该值并不唯一，故得证。或者简单来说，因为数组中不存在某个元素的值为0，所以不存在指向i=0位置的元素，那么从i=0位置的元素一定不在环里，类似于上图中链表的起始结点，只有这样才能有两个数组中的元素指向上图中的O结点，即该题的答案。如果不从i=0位置出发，则所有其他元素基本均可能被其他数指向，一定都在某个大的环里，不可能有两个指向相同位置的元素（否则环分叉），所以一个环里一定不存在相同的数字。

      比如： 
      index = [0 1 2 3 4 5 6 7]; nums=[5 2 1 3 5 7 6 4]. 
      nums[1] and nums[2] forms an isolated cycle. nums[3]=3 forms an isolated cycle. nums[6]=6 forms an isolated cycle. 
      nums[5] nums[7] nums[4] forms a cycle and nums[0]=5 is an entrance to the cycle.

• 基于以上分析，我们可以实现该解法（双指针法）获得正确答案。
• 除了双指针法，我们还可以使用二分法来进行查找，二分法的思路见链接：二分法找重复数字。对该方法，因为二分查找遍历的次数为logN，而每次更新mid值时都需要重新遍历整个数组，所以时间复杂度为O(logN)。具体实现方法可以参看代码，代码里有备注，上面的链接只供思路的参考。

51.（62:Medium）（非常经典题）Unique Paths

• 对该题自己最开始的思路便是深度优先搜索遍历DFS，但被OJ判定为“超时”，虽无法通过测试例，但其中有一些可以学到的知识，就是在搜索过程中可以不必自己创建一个网格地图存储路径，我们只要把握住网格里每个位置的特点即可，即不同的网格由(p+1)(q+1)表示（p、q代表当前访问的位置的行数与列数，且p、q的取值为[0,m-1]和[0,n-1]，与自己创建的列表地图的下标取值范围一致），当(p+1)(q+1)=m*n时代表到达终点。
• 后来参看discuss，有人提出如下的一种思路(排列组合思路)：我们从起始点到终点，无论走什么路径，走过的步数一定是(m-1)+(n-1)，即一定会向下走m-1步、向右走n-1步。这样，总共可能的路径为：从m+n-2步中选择m-1步向下走的种类数，等价于，从m+n-2步中选择m-1步向下走的种类数，即组合数C(m+n-2,m-1)或C(m+n-2,n-1)。
• 对于此题，最标准的做法其实是考虑动态规划思想。动态规划要求利用到上一次的结果，是一种特殊的迭代思想，动态规划的关键是要得到递推关系式。对于本题，到达某一点的路径数等于到达它上一点的路径数与它左边的路径数之和。即假设path数组中存储的是到达(i,j)点的唯一路径个数，则根据DP思想有：path[i][j] = path[i - 1][j] + path[i][j - 1]。又因为机器人只能向右走或者向下走，所以第一行和第一列的所有数组位置的值应为1，即只能从起始位置一直右移或一直下移才能到达各位置。这样我们只需要返回path[m - 1][n - 1]即得到了答案。对于实现，一种非常直接的方法当然是耗费O(m*n)的空间复杂度，存储到达每一个位置可能的路径数，但我们根据上面的地推公式可以发现：我们每次只需要用到上一行当前列，以及前一列当前行的信息，我们只需要用一个一维数组存上一行的信息即可，然后按行遍历，因为有m行所以遍历m次。而更新行数据的时候我们要保证row[0]=1（根据之前讨论的第一列为1的规律），因此我们其实是从每一行的第二列开始更新的。每扫描一行的时候依次更替掉上一行对应列的信息即可（因为所需要用到的信息都还没被更替掉row[j] = row'[j] + row"[j-1]，j是列指针，row'代表当前扫描行的上一行当前列的此时还没有被更新的值，row"代表当前行前一列已更新的值），所以空间复杂度是O(n)，最后返回row[n-1]。

52.（621:Medium）（非常经典题）Task Scheduler

• 由于题目中规定了两个相同任务之间至少隔n个时间点，那么我们首先应该处理的出现次数最多的那个任务，先确定好这些高频任务，然后再来安排那些次低频任务。如果任务F的出现频率最高，为k次，那么我们用n个空位将每两个F分隔开，然后我们按顺序加入其他低频的任务（比k小的频率的任务,频率越高越优先插入）。

      例如：（here X represents a space gap:）
      example1：AAAABBBEEFFGG 3  
         Frame: "AXXXAXXXAXXXA"
         insert 'B': "ABXXABXXABXXA" <--- 'B' has higher frequency than the other characters, insert it first.
         insert 'E': "ABEXABEXABXXA"
         insert 'F': "ABEFABEXABFXA" <--- each time try to fill the k-1 gaps as full or evenly as possible.
         insert 'G': "ABEFABEGABFGA"
      example2：AACCCBEEE 2
         3 identical chunks "CE", "CE CE CE" <-- this is a frame
         insert 'A' among the gaps of chunks since it has higher frequency than 'B' ---> "CEACEACE"
         insert 'B' ---> "CEABCEACE" <----- result is tasks.length;
      example3：ACCCEEE 2
         3 identical chunks "CE", "CE CE CE" <-- this is a frame
         Begin to insert 'A' --> "CEACE CE" <-- result is (c[25] - 1) * (n + 1) + 25 -i = 2 * 3 + 2 = 8

• 经过上面的例子，在插入没有“溢出”的情况下（后面讨论），完整的chunk（如：“AXXX”/“CEX”）应该出现任务中最高频率减一次，然后再加上拥有相同最高频率的任务数。如example1中，A的频率最高为4，那么“AXXX”出现了3次，最后再加上一个A，假设A的频率为k，则最短长度为(k-1)*(n+1)+1。
• 当然以上提到的都是非常理想的情况，即插入的时候没有溢出“burst”，但当发生溢出时，上面的计算方法便不再适用，如下面的例子所示。

      example4：AAABBCC 1
          you can not fill it in the way you described ABABA, because it then requires ABABACXC, total of 8 while it actually just need 7 in the form of ABACABC.

• 根据example4所述，在发生“溢出”时，我们如果按照之前完成任务的优先规则，返回的长度没有将所有的任务都执行完(如上例返回的是5而不是7)，但是正因为发生了溢出，说明我们可以合理调整间隔顺序在len(task)时间将所有任务完成，即“在len(tasks)时间完成所有任务”是可行的。又因为在没有发生“溢出”时，按如上规则排序计算所得的时间是最小的，因此我们在给出结果时，应该取len(tasks)和(k-1)*(n+1)+“kinds of the tasks with same highest frequency”之中的较大值。

53.（48:Medium）(经典题)Rotate Image

• 该题需要一些小的技巧，即要对旋转的特性非常敏感

   clockwise rotate
   first reverse up to down, then swap the symmetry
   1 2 3     7 8 9     7 4 1
   4 5 6  => 4 5 6  => 8 5 2
   7 8 9     1 2 3     9 6 3

   anticlockwise rotate
   first reverse left to right, then swap the symmetry
   1 2 3     3 2 1     3 6 9
   4 5 6  => 6 5 4  => 2 5 8
   7 8 9     9 8 7     1 4 7

54.（54:Medium）Spiral Matrix

• 我们观察到，在螺旋形访问所有元素时，遵循的搜索方向顺序为：向右->向下->向左->向上。因此，我们因沿着某一方向一直试探到该方向的终点，然后再换下一个搜索方向。因为数组矩阵中存储的都是数字，所以我们可以将访问过得位置标记为字符“x”以作区分。当经过两轮上下左右方向的试探后，之前的位置(i,j)并没有做出变化，说明该位置是螺旋访问的最后一个元素，将其加入返回列表退出循环即可。

   例如：
   1 2 3     我们从(0,0)位置开始访问，进入循环前我们将初始的访问方向设为“向右”，那么接下来我们一直会向右方向前进，
   4 5 6     直到到达(0,2)位置，此时是当前“右方向”的尽头，于是我们将试探方向改为“向下”同样访问到(2,2)位置再换为
   7 8 9     “向左”。需要注意的是，当我们访问到(1,0)位置时，因(0,0)已访问过，所以此时就应该将方向调为"向右"。

• 另外一种思路：我们来自己画一个螺旋线的行走轨迹。我们会发现，螺旋始终重复四个遍历过程，向右遍历（列递增）-->向下遍历（行递增）-->向左遍历（列递减）-->向上遍历（行递减）。但是在螺旋线行走的过程中，我们的行列的上下边界一直在变。所以我们维护四个变量，rowBegin, rowEnd, colBegin, colEnd. 我们用这个四个变量来指示遍历时的边界。遍历终止条件是rowBegin > rowEnd || colBegin > colEnd. 需要注意的是，我们在向左遍历和向上遍历时，需要判断遍历的行或者列是否存在，避免重复。具体实现的链接：另一种思路

//下面的解法不需要特殊考虑corner case，interview friendly
public List<Integer> spiralOrder(int[][] matrix) {
    List<Integer> res = new LinkedList<>();
    if (matrix == null || matrix.length == 0) return res;
    int n = matrix.length, m = matrix[0].length;
    int up = 0,  down = n - 1;
    int left = 0, right = m - 1;
    while (res.size() < n * m) {
        for (int j = left; j <= right && res.size() < n * m; j++)
            res.add(matrix[up][j]);

        for (int i = up + 1; i <= down - 1 && res.size() < n * m; i++)
            res.add(matrix[i][right]);

        for (int j = right; j >= left && res.size() < n * m; j--)
            res.add(matrix[down][j]);

        for (int i = down - 1; i >= up + 1 && res.size() < n * m; i--)
            res.add(matrix[i][left]);

        left++; right--; up++; down--;
    }
    return res;
}

55.（59:Medium）Spiral Matrix II

• 该题的解题方法与上面的54题(54)没有太大差别。因为题目要求数组中的元素是[1, n^2]，所以我们可以先初始化一个元素全为0的n*n矩阵，如果位置上元素为0则代表可访问。我们仍然按螺旋形的搜索顺序来访问这个初始化的全0矩阵，每访问一个位置，我们将cur(存储当前位置应该存放的数)的值+1直到n^2为止。

56.（153:Medium）（经典题）Find Minimum in Rotated Sorted Array

• 不知道这个题想考察什么，只需要比较nums[0]与nums[-1]的大小。如果nums[0]<nums[-1]，说明输入的数组是升序的，直接返回nums[0]；如果nums[0]>=nums[-1]，说明输入的数组已经被旋转过，只要从头开始遍历，若nums[i]>nums[i+1]，则直接返回nums[i+1]即可。
• 以上的思路其实是不和规则的，题目想考察“二分查找”的应用。传统的二分查找是给定目标值key，在数组中查找是否有指定的数字并返回下标索引，但此处的二分查找却略有不同，题目没有给定key，而是要求我们查找一个事先未知的最小值。这里我们同样要设立三个指针low、mid、high，每次循环都比较nums[mid]和nums[high]的大小，需要注意在rotate前数组是严格升序的，所以以下的判断依据才成立：当nums[low]<nums[high]时，说明数组中的最小值在前半部分，置high = mid，这里不是high=mid-1是因为不能确定nums[mid]是否是在nums[0...mid]中的最小值，无法排除；相反的，当nums[low]>=nums[high]，说明数组中的最小值应在数组的后半部分，置low=mid+1，不是low=mid是因为即使nums[mid]=nums[high]均是最小值，但我们也可以返回nums[high]而不必非是nums[mid]。

57.（718:Medium）（经典题）Maximum Length of Repeated Subarray

• 该题的思想是“移动对比”，即以一个数组作为参照物，另外一个数组从最左侧移动到最右侧，寻找当前位置下的最大子数组长度，示例如下：

   A = [X,X,X,X,X,X]      B = [X,X,X,X,X]
   A、B进行对比的效果如下所示（上面为A，下面为B）：
           [X,X,X,X,X,X]   =>      [X,X,X,X,X,X]   =>        [X,X,X,X,X,X]  =>     [X,X,X,X,X,X]   =>
   [X,X,X,X,X]               [X,X,X,X,X]                 [X,X,X,X,X]             [X,X,X,X,X]  
   --------------------------------------------------------------------------------------------------  
   [X,X,X,X,X,X]   =>   [X,X,X,X,X,X]  =>  [X,X,X,X,X,X]  =>   [X,X,X,X,X,X]   =>  [X,X,X,X,X,X]   =>
   [X,X,X,X,X]            [X,X,X,X,X]        [X,X,X,X,X]           [X,X,X,X,X]           [X,X,X,X,X]
   --------------------------------------------------------------------------------------------------
   [X,X,X,X,X,X]       =>  [X,X,X,X,X,X]
           [X,X,X,X,X]               [X,X,X,X,X]

• 我们这里设置了i、j两个指针分别指向A和B数组，当len(A)-i>=maxLen时才有必要继续移动B数组，否则当前的有效长度已经比maxLen小了，即使后面的字符全部匹配也不是最长的长度，此时退出循环即可。
• 第二种思路“动态规划”：Same idea of Longest Common Substring。

该题动态规划的思路并没有研究，需要在复习时继续深入理解。

58.（64:Medium）（经典题）Minimum Path Sum

• 该题与51题（62）的解法类似，均是动态规划问题。与之不同的是，我们在更新到达某个位置的最短路径和时，应该取"从上方来的"和"从左侧来的"的最小值，再加上该位置的值grid[i][j]即为从(0,0)到(i,j)的最短路径和。
• 在解答该题时，与第51题（62）类似，我们同样可以将空间复杂度从O(mn)降到O(n)，即保存一行的最短路径值即可。

59.（611:Medium）（非常经典题）Valid Triangle Number

• 暴力解法被OJ判为超时
• 个人认为该题还是“三指针问题”：首先要先对nums进行排序，这一步非常重要，即假设下标x<y<z，则若nums[x]+nums[y]>nums[z]，则一定有nums[y]-nums[x]<nums[z]，因为nums[y]<nums[z]是排序后数组元素的性质，且数组中哥元素全非负，故两边之差小于第三边一定成立。接下来，我们先设置一个最右侧的指针i，初始值为len(nums)-1，然后再设置两个指针p、q，初始值分别为0和i-1。当nums[p]+nums[q]>nums[i]时，说明nums[p,...,q-1]+nums[q]>nums[i]也成立，因为数组是升序的，故nums[p,...,q-1]>=nums[p],在当前i、q的位置下，便有q-p个组合满足三角形三边条件。然后，我们在q-1>p的情况下，将q减一，p不变(因为此时nums[p]+nums[q]还不一定比nums[i]大，若将p设为0，则nums[p]、nums[q]均减小，和一定小于nums[i])，然后同样按上面的思路做判断。当然，存在一种情况，现有的p、q、i不满足nums[p]+nums[q]>nums[i]，因为，此时若固定q、i不变，p=0，nums[p]+nums[q]的和是nums[p,...,q-1]+nums[q]中最小的，所以此时只需要在p+1<q的前提下将p加一，再次判断是否满足两边之和大于第三边的条件即可。最后，若某一时刻q-1=p，那么在i>2的条件下(保证nums[i]前至少有两个数即两条边)，将i=i-1，p=0，q=i-1，然后按上面所述思路开启新一轮的循环即可。
• 关于上面的“三指针”在这里谈一些指针初始化设置的技巧：1、首先，q指针初始化的值永远为i-1，p指针的值初始化值永远为0，保证了当nums[p]+nums[q]>nums[i]时，没有必要继续遍历判断p+1至q-1的元素（比暴力解法节省时间的地方，因为元素是递增的）。同样，假如我们将q的值初始化为p+1，那么若当前的nums[p]+nums[q]>nums[i]，则nums[q+1]至nums[i-1]也满足条件，不需要继续遍历，只不过此时的p、q起到的作用与q初始化为i-1时相比角色发生了互换而已。相似的，我们也可以将i设置为2，然后将i的值从2一直遍历到len(nums)-1，道理是相似的。总结起来，我们总是将两个指针指到了当前扫描子数组的一头一尾的位置，只有中间的指针（形象表述，并不严谨）进行移动，即“掐头去尾变中间”。2.要想运用技巧1里面的指针前后移动必然引起的数组元素值的线性大小变化，前提就是要将nums数组进行“排序”。

60.（560:Medium）（经典题）Subarray Sum Equals K

• 最优的算法总是从最原始粗暴的解法开始，通过挑选合适的数据结构、合理的技巧省去中间冗余的步骤进而优化得来的。
• 该题用到的一个巧妙技巧（根据连续数组元素的特性）：设置一个列表数组sumArr，在sumArr[i]存储从nums[0]到nums[i]的所有数之和。这样，在i<j，计算sumArr[j]-sumArr[i]时，求得的是从nums[i+1]到nums[j]该段子数组的各元素之和。基于以上的子数组方式转化，我们没有必要从nums[0]开始，计算长度为1...n的各子数组元素和，再从nums[1]开始计算1...n-1的各子数组元素和，按这样的规律直到nums[n-1]。
• 基于上面的技巧，我们从0开始遍历nums数组，当访问nums[i]时，我们可以求得对应的sumArr[i],并从下标0开始扫描到i-1，观察sumArr[0...n-1]中是否有与sumArr[i]-k相等的值(代表以nums[i]结尾，非nums[0]开头的子数组)，需要注意sumArr[i]-sumArr[0]其实是以nums[1]开头的，所以为了包含nums[0]开头的情况，我们需额外判断是否sumArr[i]=k。可惜的是，每访问到nums[i]，都要从0开始将sumArr[i]以前的元素都搜索一遍，这样的实现是“超时”的。
• 为了继续沿用上面的思路，需要想一个更高效省时的方法，关键点就是如何节省“从0开始遍历sumArr寻找sumArr[i]-k”的时间。在这里，我们想到了之前做过的第31题（1）的技巧，我们用一个字典，保存已经计算出的sumArr[m]值(m代表数组中任何位置)，即以sumArr[m]作为key，以sumArr[m]在sumArr数组中当前位置i以前出现过得次数作为value，所以我们也可以将该题的题目改为“X Sum”。这样，我们只需要判断sumArr[i]-k是否在字典中，若存在，那么直接将满足条件的子数组个数count值加上对应的value即可。然后再在字典中增加sumArr[i]的键值对。需要注意的是：我们必须在判断完sumArr[i]-k是否在字典中之后，再将sumArr[i]添加到字典中，因为可能会出现sumArr[i]-k=sumArr[i]的情况，若把该次数算在内，代表“长度为0的子数组，其元素值的和为k”，这显然是不合法的。

61.（380:Medium）（经典题）Insert Delete GetRandom O(1)

• 该题考察的实际是对数据结构的掌控。我们知道，数组列表的获取、添加是在O(1)时间复杂度内可以完成的，但我们在添加元素、删除元素时，一方面需判断目标元素是否在列表中存在，另一方面在获取元素时不能直接返回某一个指定的值的索引，此时如果只用数组列表这一个数据结构，又必须从头开始遍历，显然不满足O(1)复杂度，因此，我们还需要借用字典的数据结构（字典不适合随机读取）。
• 我们用字典存储val及其在列表中的对应下标，即(val, val在列表中下标)，因为我们在向列表中插入某个val值时，该val值一定添加到了列表的末尾，所以其索引应为当前未添加val时的数组列表长度len(list)。而当删除某个指定元素的时候，列表元素的下标会发生变化，而字典中key的值val存储的是对应key在列表中的下标索引，一旦从列表“中间”删除某个元素，则该元素之后的元素在字典中的val值均需要减1，不满足O(1)时间复杂度。所以为了避免大范围的更改字典中存储的索引值，我们将要删除的val和列表中最后一个元素list[-1]互换，这样我们只需要改变key为list[-1]的字典值（下标索引）即可，然后在列表数组末尾删除指定的元素。而随机读取则比较简单，只需要产生一个0到len(list)-1的随机数即可，然后把该随机数当做索引访问列表数组中的元素。

62.（75:Medium）（经典题）Sort Colors

• 该题最简单的解决方法就是扫描数组列表两次，第一次统计出0、1、2的个数，第二次是按个数建立一个新的列表并赋给nums。
• 此外还有1-pass的方法，即将所有0放到最左边，所有2放到最右边。我们设定两个指针p0和p2，分别指向下一个放0和下一个放2的位置，这样，凡是遇到nums[i]为0或2的时候，将其交换到正确的位置上去，若为1则直接略过，最后1自然就位于数组的中间了。注意我们每次在进行交换的时候，一定要保证i>p0或i<p2，这样交换的结果才有意义。

该题还有一种叫做平移插入的方法，没有研究，等下次复习时再看

63.（162:Medium）（非常经典题）Find Peak Element

• 这道题最简单的方法，当然是从头开始搜索数组元素，一旦nums[i]>nums[i+1]，则说明nums[i]至少是一个局部的极值点，直接返回下标i即可。但这种方法并不是logarithmic complexity，即logn的。
• 为了将时间复杂度降至logn，我们最先想到的应该就是分治思想，再联想第56题（153）的应用场景，那么应该是可以用二分查找来解决该问题的。只是两道题的区别在于：56题是在全局严格升序的基础上进行查找，而该题显然并不是全局有序的，但好处是题目说明“如果有多个极值点，可以返回任何一个即可”，这句话又可转述为“数组是局部有序的，即数组是由多个局部有序的子数组组合而成的”，因此我们可以利用二分查找思想来解决该问题。首先设置两个指针low、high分别指向数组的首和尾，当low<high时才进入循环，因为我们找的是极值点，所以若nums[high]<=nums[low]或者nums[high]<nums[high-1]时，最终返回的极值点绝不是当前的high，所以我们将high的值减一直至nums[high]>nums[low]且nums[high]>nums[high-1]，这样我们再比较mid指针的元素和nums[high]的大小，找到极值元素。
• 其实上述的思路是有问题的，因为当“nums[high]>nums[low]且nums[high]>nums[high-1]”条件满足时，high的位置至少已经是一个局部的极值点了,从而上面的解法转化成了第一种时间复杂度为O(n)的解法。正确解法应为：我们每次比较nums[mid]和nums[mid+1]的值，如果中间元素大于其相邻后续元素，则中间元素左侧(包含该中间元素）必包含一个局部最大值，high = mid。如果中间元素小于其相邻后续元素，则中间元素右侧必包含一个局部最大值，low = mid+1。

64.（795:Medium）（非常经典题）Number of Subarrays with Bounded Maximum

• 这道题要找出所有满足条件的continuous子数组，一开始想到的思路是“深度优先搜索DFS”，想法类似于之前leetcode中的78、216题，遍历所有可能的子数组（注意一定是位置连续的，若位置不连续，应设置返回值来提前中止该路径上后续的遍历操作），累计符合条件的子数组数量最后返回，可惜该方法超时。
• 受到深度优先搜索和位置连续数组的启发，又想到应该使用“堆栈数据结构”，通过入栈操作保证了数组的连续性，再使用上面max()函数得出当前栈中最大元素是否满足条件，最后即可得出以元素A[i]开头的满足条件的子数组数量。关键问题同DFS一样，当i取每一个值时，不能运用i以前的情况来推测当前以A[i]开头的满足条件的子数组数量，所以不得不重新进行后续的遍历操作，非常耗时，也是“超时”的解法。
• 通过OJ的思路是：我们发现凡是满足条件的子数组，其开头的元素A[m]均是小于等于R的，而其末尾的元素A[n]也同样是小于等于R的。区别在于，当A[n]<L时，我们在总的count值上加的是“n位置以前最近的某个x，满足以A[x]为尾且A[x]在L、R之间”的子数组长度length，换句话说，当前的A[n]作了前面length个满足条件的子数组的“嫁衣”，在计算总的count值时，A[x+1]至A[n]间任意相邻元素不能单独算作满足条件的连续子数组；而当A[n]在L、R之间时，A[m]至A[n]间的元素可以组成n-m+1个满足条件的均以A[n]结尾的连续子数组，而此时的n-m+1其实就是另一种情况中的length。而当我们遍历到某个位置i时，A[i]>R，则需更新m值为i+1，length重置为0。按照这样的思路，我们非常高效的利用了之前的遍历信息，大大减少了运行时间。
• 启示：其实以上谈到的思路在无限时间内均可行，但只有第三种思路是利用了之前遍历的历史信息，且使用了下标索引的方式巧妙记录了历史信息。

该题应还有其他解法，第三种实现只beat 15%，在下次复习时应该研究理解其他更巧妙的思路

• 该题高效的解题思路如下：

    /*
    the explanation is: in every iteration, we add the number of valid subarrays that ends at the current element.
    For example, for input A = [0, 1, 2, -1], L = 2, R = 3:
    for 0, no valid subarray ends at 0;
    for 1, no valid subarray ends at 1;
    for 2, three valid subarrays end at 2, which are [0, 1, 2], [1, 2], [2];
    for -1, the number of valid subarrays is the same as 2, which are [0, 1, 2, -1], [1, 2, -1], [2, -1];
    */
    public int numSubarrayBoundedMax(int[] A, int L, int R) {
        int j=0,count=0,res=0;
        
        for(int i=0;i<A.length;i++){
            if(A[i]>=L && A[i]<=R){    //A[j],...,A[i] 所有从j开始，以i为尾的子数组有i-j+1个，即j...i;j+1..i;j+2..i;...;i-1..i;i
                res+=i-j+1;count=i-j+1;
            }
            else if(A[i]<L){    //设从j到i的最大元素为max,则有效子数组为j..max..A[i];j+1..max..A[i];j+2..max..A[i];...;max-1 max..A[i];max...A[i]，count是i-max时i-j+1的长度
                res+=count;
            }
            else{
                j=i+1; //将j指针后移，count值清零
                count=0;
            }
        }
        return res;
    }

65.（90:Medium）Subsets II

• 该题用第49题（78）相同的代码即可通过OJ，但只能beat 48%的人。

该题与第49题（78）应有其他更高效的方法，在下次复习时应仔细研究学习理解

66.（670:Medium）Maximum Swap

• 该题好似小学数学题中的一个题目。因为在整数int数上执行单个数字的交换非常复杂，理所应当地，我们应将num数字转化为一个列表listNum，而每一个列表中的元素代表原数字num中的一位。因为题目中给出了，当当前数字的排列已经是最大时，我们不需要进行任何的交换操作，直接返回num即可，而该判断的本质，其实可以将转化的listNum进行降序排序，若与原listNum相等，则说明输入的num已是最大。
• 既然已经判断输入的num一定不是最大的，那么我们就应该遍历这个listNum，记录每一个数字及其对应的在listNum中的下标位置。这里我们需要注意一点，例如：num=4776，做一次交换得到的结果应该是7746而不是7476，即若有相同的最大元素，我们应优先于位数低的进行交换。这样，我们从低位向高位进行遍历，并用一个字典dict存储listNum中不同位数字及其相应的下表索引（方便元素的一次性读取而不用再次遍历），当遇到某个数字已经存在于字典dict中，说明该数字处于高位，我们跳过它即可。这样，我们将建好的字典的key（listNum不同位的数字）进行降序排列得到sortedDigits，并与listNum的各个比较，便可以得到需要交换的两数位置。需要注意，可能listNum[0]就是各个位数中最大的(即与sortedDigits[0]相等)，如：num=7235或7317，这个时候我们应分为两种情况：1、listNum[0]代表的数字在数组中只出现过一次，这时候，我们应选取次大的元素sortedDigits[1]与listNum[1]按照相同的规则进行比较 2、listNum[0]可能在数组中出现过多次，又根据我们建立字典的规则，字典中dict[listNum[0]]指向的val值（下标索引）一定不是0，而是最低位的listNum[0]出现的位置，这样我们不移动指向sortedDigits的指针，只向后移动指向listNum的指针，比较listNum[1]与sortedDigits[0]的值。而之后每次的比较均遵循上述两种情况的原则，直到找到满足条件的两个交换位置为止。交换后按10的不同次幂将各个位加和返回即可。

67.（729:Medium）（非常经典题）My Calendar I

• 该题拿到手后，第一个想法就是维护一个数组列表list，其中保存已预订时间的所有日期，如book(start=10,end=15)，则list中存储[10,11,12,13,14]，当再次预定时，我们从start开始遍历，判断当前遍历到的日期是否在list中，若从start到end-1的日期都没有被预定，我们则返回True，否则返回False，但该数据结构的操作被判定为“超时”。
• 使用列表的过程我们每插入一次，都需要重新遍历list列表一次，非常耗时，后来考虑若用集合的数据结构，我们只需要建立一个存储从start到end-1的集合，通过与存储已经预定时间的set集合作交集，即可判断是否有重合，但该方法仍被OJ判为“超时”。后来，思考若在列表数据结构的基础上进行预定日期重叠情况的分类讨论，但仍“超时”。本质上，上面三种思路的时间复杂度均为O(n^2)。
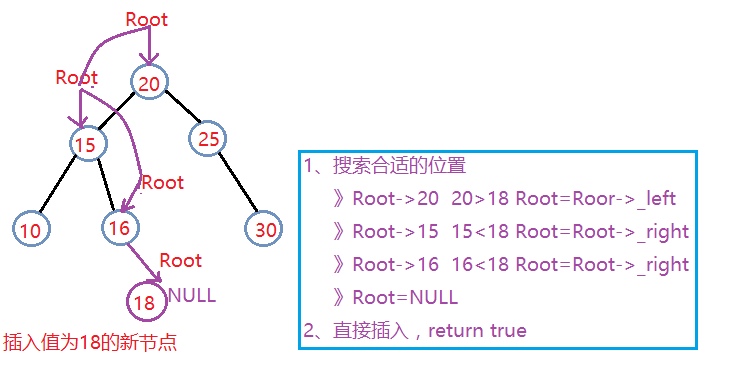
• 正确的思路为：使用“二叉搜索树(Binary Search Tree)”的结构。二叉搜索树的搜索,插入,删除操作的复杂度等于树高，O(log(n))。下图展示了搜索及插入操作。
• 正如上图所示，我们本题其实就是一个二叉树的“插入操作”，区别仅在于树的结点并不是一个特定的值，而是一个区间，小于结点区间的最小值的结点则插入到当前结点的左子树上(end<=node.start)，大于结点区间最大值的结点则插入到当前结点的右子树上(start>=node.end)，否则，说明待插入结点与当前结点的区间范围重合，直接返回False。
• 注意：当树的根节点root为空时(root=null)，要将第一个预定的区间作为根节点插入树中。

该题除了二叉搜索树应还有其他方法，复习时需要仔细研究学习

<68>.（731:Medium）（非常经典题）My Calendar II

• 该题原本想利用第67题（729）的思路进行求解，只是在node结点上增加一个变量标记该结点是否为double booking的，若输入的[start,end)与[node.start,node.end)是重合的，则我们将当前node的区间值更新为[max(start,node.start),min(end,node.end))，并将该结点标记为double booking，并将切割剩余的两边部分分别传递到该node结点的左右子树上进行深度的搜索查找，看看有没有和其他的结点区间重合。但可惜该方法并不能通过OJ，原因不明。
• discuss中普遍采用的方法为：We store an array self.overlaps of intervals that are double booked, and self.calendar for intervals which have been single booked. We use the line start < j and end > i to check if the ranges [start, end) and [i, j) overlap.The clever idea is we do not need to “clean up” ranges in calendar: if we have [1, 3] and [2, 4], this will be calendar = 【【1,3】,【2,4】】 and overlaps = 【【2,3】】. We don’t need to spend time transforming the calendar to calendar = 【【1,4】】.（该思想理论上也可以作为第67题(729)的另一种解法）
• 上面的方法，有两个非常关键的地方：1、将once-booking的事件与double-booking的事件区分开来用两个数据结构来存储，每次插入新事件时先在overlaps集合中查找是否有重叠，如果没有再在calendar集合中查找是否有重叠，若存在则将重叠区间插入overlaps集合，而将当前的事件插入calendar中。2、提取的判定时间区间是否重叠的判断条件非常简练，即start < j and end > i，简单来说就是not(end <= i or start >= j)。 在通过的测试程序中，有模仿上面两个列表的方法实现的二叉搜索树的解法，具体可以参看代码。

该题其实也可以使用二叉搜索树的结构来求解，但需要用到lazy propagation的知识，并没有理解，需要在复习时再深入研究

<69>.（11:Medium）（非常经典题）Container With Most Water

• 该题一开始使用深度优先搜索DFS，超时，若使用两个for循环的暴力解法，理论上应该也是超时的，因为他们都是进行了两层的遍历，时间复杂度均为O(n^2)。
• 正确的解法是应用“双指针思想”，在继续下边的分析之前，我们需要明确一个该题的注意点，即假设现在有一个容器，则容器的盛水量取决于容器的底和容器较短的那条高。那么，为了将两个for循环的暴力解法时间复杂度降低，我们就应该利用这个性质，省去没有必要的遍历，并且确保所需的答案一定能被遍历到。这样的话，我们可以从最大的底长入手，即当容器的底等于数组的长度时，则容器的盛水量为较短边的长乘底，那么当底足够大时，影响容积的因素在于较短的高，这样就把两个变量减少到了一个变量了。主要的问题在于“如何移动双指针才能保证最大的盛水量被遍历到”或“怎样移动指针才能保证计算是有效的”，我们假设“当前右边指针right的线段比左边指针left的线段高”，假如我们将右指针左移，则右指针左移后的值和左指针指向的值相比有以下三种情况：

   1.右指针指向的值大于左指针
     这种情况下，容器的高取决于左指针，但是底变短了，所以容器盛水量一定变小
   2.右指针指向的值等于左指针
     这种情况下，容器的高取决于左指针，但是底变短了，所以容器盛水量一定变小
   3.右指针指向的值小于左指针
     这种情况下，容器的高取决于右指针，但是右指针小于左指针，且底也变短了，所以容量盛水量一定变小了

• 基于以上分析，容器高度较大的一侧的移动只会造成容器盛水量减小，所以应当移动高度较小一侧的指针，并继续遍历，直至两指针相遇。

70.（289:Medium）Game of Life

• 该题分析起来还是比较简单的，解题的关键在于，要保证所有细胞的更新是同时的，即“the board needs to be updated at the same time: You cannot update some cells first and then use their updated values to update other cells”，这样便要求我们在处理遍历完一个细胞后，不能将其状态立马更新到下一状态（0或1），而应保证更新后的状态不仅能表示原来的活性，又可以标记出下一个状态的活性。这里，我按照以下规则来做更新："活(1)->死(2)"，"死(0)->活(-1)"，"活(1)->活(1)"，"死(0)->死(0)"，这样，更新前后的正负性没有发生改变，我们又可以根据更新后的值判断该细胞到底是死还是活，而其他细胞判断周围cell活性的条件也变为if(board[x][y] > 0)。当遍历完所有细胞后，再次遍历一遍board，将状态数值调整到合适的0、1值即可。

该题可能还有其他更简单的在O(mn)以内完成的方法，下次复习时需再研究

71.（80:Medium）（经典题）Remove Duplicates from Sorted Array II

• 第一种方法和Leetcode 第26题“Remove Duplicates from Sorted Array”相似，设置两个相邻的前后指针i1、i2，分别进行i1与i2、i2与i2+1的元素比较，若有连续三个元素相同，则删除i1位置的元素，注意，此时i1、i2的指针位置不能发生变化，因为删除数组中间的某个元素后，后面的元素下标均会减1。若连续三个元素不相同，则分别使i1+1、i2+1即可，时间复杂度为O(n)（只beat 50%，说明还有更快的方法）。
• 第二种方法的时间复杂度也是O(n)，但与第一种方法相比，它没有真正的删除nums数组中的元素，而只是将数值重复三次以上的位置用后边满足条件重复次数少于等于两次的元素所代替，即nums=[1,1,1,2]，返回的length=3，修改后的nums=[1,1,2,2]，这样按返回值length打印出前length个元素的数组为[1,1,2]。实现方法也很简单，即维护两个指针，逻辑上，一个指向传入的未修改的nums数组，一个指向真正有效的nums数组（因为是in-place的，所以物理上两指针其实指向的是同一数组）。

两种方法都很像“双指针法”，至于什么是真正的“x指针法”，需要复习时再做研究，确定具体定义。

<72>.（73:Medium）（非常经典题）Set Matrix Zeroes

• 该题的空间复杂度从O(mn)、O(m+n)到O(1)都有，但时间复杂度，全网包括discuss中的答案基本都需要至少执行两遍深度为2的嵌套for循环，第一遍记录元素为0的信息（或那些行列需要置0），第二遍才根据第一遍存储的信息进行真正意义上的行列清零操作。下面我会根据空间复杂度由高到低排序给出三种不同的解法，包括我最初的想法以及空间复杂度简化的改进分析。
• 空间复杂度为O(mn)：因为我们要将矩阵中的0元素所在行列位置进行置0操作，所以开始时思考是否能在时间复杂度O(mn)内解决该问题，即只遍历矩阵一遍，后来发现，因为0元素位置可能在行列的起始点，也可能在行列中间，当元素位置为后一种情况时，我们必须在之前两层for循环的基础上再加一层甚至两层的for循环（即深度为3或4层），才能将当前遍历的0元素所在行列位置都清零，显然企图一次遍历解决问题是不可行的。既然如此，不如第一次遍历记录矩阵中所有0元素的行列位置，第二次根据0元素的行列位置遍历矩阵并清零，这样当矩阵为全0矩阵时，空间复杂度最坏为O(mn)。
• 空间复杂度为O(m+n)：在看了discuss后，进行反思：根据分析，只要某个位置(i,j)的元素为0，第i行、第j列都会清零。我们只需将第一种空间复杂度为O(mn)的方法再改进一下即可，即，若元素为0的位置在同一行或同一列上，我们就不需要再多次重复记录同一行或同一列记录，这样空间复杂度便会降低。换句话说，我们只要记录元素为0的行位置、列为值即可，即“记录的最小单位是一个行或一个列，而不是一个点”。
• 空间复杂度为O(1)：该思路是discuss中获得票数最高的答案，简单理解为，在第一次遍历矩阵时，若位置为0的元素位置是(i,j)，即我们应该在第二次遍历矩阵时将第i行、第j列全部清零，而此时，我们并不将它的行列信息保存在额外的列表中，而是将它的位置信息保存到matrix[i][0]和matrix[0][j]，即将该位置所在行的第一个元素置True(或其他符号)，该位置所在列的第一个元素置True(或其他符号)。该法的巧妙之处在于，将0元素的信息全部都移到了行列的首位置，化解了第一种方法里“0元素可能在行列中间而不能一次遍历解决问题”的难题。需要注意的是，因为第0行的信息和第0列的信息都会存储在(0,0)位置，所以，我们假设(0,0)只存储第0行的信息，而由另外设置的变量col0存储第0列的信息，这样便解决了“冲突”。该法我并有亲自实现，具体的解释及代码请参看链接：O(1)时间复杂度解决“矩阵置0”问题

73.（120:Medium）（非常经典题）Triangle

• 该问题一开始拿到时，立马想到的就是DFS，因为整个三角形其实可以抽象看成一个树，从而向下深度搜索所有路径并取其中的最小值，这种解法相当暴力，与两层for循环无异，时间复杂度应为O(n^2)，空间复杂度应该在O(2^n)，被OJ判为超时。
• 其实之所以只想到了上面的思路，是因为我们观察的范围太窄，只限于从上到下每一层取一个结点找一个最小路径，没有考虑同层的其他结点。从宏观上看，我们会发现，从i层的子节点向下搜索路径其实是i-1层的子问题（或者形象的看成子树）。于是我们便可以利用这些子问题的求解从而得出最上层[0,0]位置的root结点的最短路径，即“动态规划DP思想”。那么，为什么使用的是“bottom-up”而不是“top-down”呢？其实若以“top-down”进行求解，思路又变回了DFS搜索，若已知到达i层结点的各个路径，那么到达i+1层的各个结点路径已经是确定的，即已知path(i,j)[这里不能使用minpath因为我们当前并不知道从(0,0)到(i,j)的路径是不是最短的，即使我们选取的都是当前结点可选的最小值，凭这一点也不能使用top-down]，path(i+1,j)、path(i+1,j+1)的值是唯一确定的，且会发生“值重叠”的现象，如path(i,j)既可以为path(i-1,j)+trangle(i,j)也可以为path(i-1,j-1)+triangle(i,j),故若用DP问题求解（需要记录所有之前的情况），只能采用“bottom-up”思路，即最底层的minipath即使结点值，对于上层的结点，其miniPath(i,j)=min(minipath(i+1,j),minipath(i+1,j+1))+triangle(i,j)，这样最后返回minipath(0,0)的值即为最短路径值。使用“bottom-up”思路，我们可以不借助额外空间，直接在triangle数组上进行修改即可。

该题非常有助于对DP问题的理解，建议参看《算法导论》中关于“动态规划”的定义以及其与“分治思想”的区别与联系，理解DP问题及其应用场景。

74.（74:Medium）Search a 2D Matrix

• 该题较简单，需要注意的是，虽然每行第一个元素都比上一行第一个元素大，但不能保证，每行后边的每个元素都比上一行后边的每个元素大，所以我们需要判断当该行第一个元素小于等于target时才再该行搜索，若该行第一个元素比target大，则直接跳出循环返回False即可。
• 这里可以进行优化的地方是，我们在搜索每一行的时候，因为行严格有序，可以使用“二分查找”来提高搜索速度。

75.（105:Medium）（经典题）Construct Binary Tree from Preorder and Inorder Traversal

• 该题主要考察数据结构（树）方面的知识，根据前序及中序遍历结果建树。
• 我们发现树（或子树）的前序遍历的第一个结点总是指向根结点，而树（或子树）的中序遍历总是以根节点为中心将序列分成左子树遍历序列与右子树遍历序列。因此，我们可以从前序遍历中获取根节点，而从中序遍历中获取左右子树，递归的由下到上建树。问题是：前序遍历“根..(左子树)....(右子树)..”，在递归的过程中我们得到了该子树的根节点后，继续向后访问只能获取到左子树的根节点，而因为不知道左子树的结点个数是多少，所以无法直接跳过左子树的遍历序列获取到右子树的遍历序列，这就要求我们在递归过程中统计左子树、右子树的结点个数，从而在向递归函数的上一层返回时，让上层的调用函数根据左子树结点数获得右子树的根节点。在递归过程中，我们可以传入标记参数tag来指示此时是在建立左子树还是右子树。
• 看了discuss后，在这里对以上的思路做一些补充，从而可以省去对左右子树结点个数的统计。

1. I hope this helps those folks who can’t figure out how to get the index of the right child:
2. We know the index of current node(root node) in the preorder array - preStart (or whatever your call it), it’s the root of a subtree
3. Remember pre order traversal always visit all the node on left branch before going to the right ( root -> left -> … -> right), therefore, we can get the immediate right child index by skipping all the node on the left branches/subtrees of current node（root node）
4. The inorder array has this information exactly. Remember when we found the root in “inorder” array we immediately know how many nodes are on the left subtree and how many are on the right subtree
5. Therefore the immediate right child index is preStart + numsOnLeft + 1 (remember in preorder traversal array root is always ahead of children nodes but you don’t know which one is the left child which one is the right, and this is why we need inorder array)

76.（792:Medium）（经典题）Number of Matching Subsequences

• 一开始没有审清楚题，以为是考察字符串匹配的算法，所以好长时间在温习研究KMP算法，结果回国头来才发现是序列，不要求连续在目标字符串中是连续的（关于KMP的算法实现和参考链接均在该题的代码注释中，建议巩固）。
• 第一种方法也是最简单的方法当然还是暴力解决，只不过这里的word是目标待匹配字符串，而S则是要拿来和word来匹配的，结果当然是被OJ判为“超时”。
• 通过暴力方法，我们会发现匹配过程中主要的时间都花费在从S中寻找对应的字符，而且对于word如"abac"，第一个a扫描找到后，第二个b又必须从找到a的地方重新开始找，而不能一次性找到。为了节省时间，这便要求我们建立一个哈希表（一次存取），将S中各个字符的位置都保存到字典中，当我们找到a时，记录当前a的位置indxs，那么在找b的时候，先从字典中取出存放b的位置列表，遍历是否有一个放b的位置刚好比indxs(之前放a的位置)大，从而保证序列的顺序没有改变。举例如下：

   The idea is to use the String S and build a dictionary of indexes for each character in the string.
   Then for each word, we can go character by character and see if it is a subsequence, by using the 
   corresponding index dictionary, but just making sure that the index of the current character occurs 
   after the index where the previous character was seen. To speed up the processing, we should use 
   binary search in the index dictionary.

   As an example for S = "aacbacbde"
   dict_idxs ={a: [0, 1, 4]，b: [3, 6]，c: [2, 5]，d: [7]，e: [8]}
   Now for the word say “abcb”, starting with d_i = 0,
   a => get list for a in the dict_idxs which is [0, 1, 4], and in the list, find the index of a >= d_i 
        which is 0. After this update d_i to +1 => 1
   b => get list for b in the dict_idxs [3, 6], and in the list, find the index of b >= d_i => >= 1, 
        which is at index 0 => 3, after this update d_i to 4+1 => 4
   c => in the list for c, [3, 5], find the index of c >= 4, which is 5. update d_i to 5+1 = 6
   b => in the list for b, [3, 6], fund the index of b >= 6, which is 6, update d_i to 7, since this is 
        the end of the word, and we have found all characters in the word in the index dictionary, we 
        return True for this word.

• Tips：Python中，有一种字典它本身提供了默认值的功能，即collections.defaultdict类，defaultdict类的初始化函数接受一个类型作为参数，即defaultdict类就好像是一个dict，但是它是使用一个类型来初始化的，当所访问的键不存在的时候，可以实例化一个值（初始化时接收的类型）作为默认值。

第二种实现只beat了10+%的人，可能还有其他更高效的实现，在下次复习时需要学习

• 一种非常高效巧妙的思路：

    public int numMatchingSubseq(String S, String[] words) {
        Map<Character, Deque<String>> map = new HashMap<>();
        for (char c = 'a'; c <= 'z'; c++) {
            map.putIfAbsent(c, new LinkedList<String>());
        }
        for (String word : words) {
            map.get(word.charAt(0)).addLast(word);  //先将每个单词完整的存储进去，代表从每个单词的第一个字符开始匹配
        }

        int count = 0;
        for (char c : S.toCharArray()) {
            Deque<String> queue = map.get(c);
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                String word = queue.removeFirst();
                if (word.length() == 1) { //说明该word之前的部分已全部匹配
                    count++;
                } else {
                    map.get(word.charAt(1)).addLast(word.substring(1));  //一种很好的进行subsequence后续cut比较的思路
                }
            }
        }
        return count;
    }

77.（106:Medium）Construct Binary Tree from Inorder and Postorder Traversal

• 该题与第75题（105）思路基本一模一样，除了后序遍历的根是在序列的末尾位置，所以在此不做过多的赘述。

按之前75题的方法解决该题只beat 37.5%的人，需要在下次复习时学习是否有更快的方法

78.（33:Medium）Search in Rotated Sorted Array

• 该题与第56题（153题）极其类似，只不过我们需要进行两次“二分查找”的操作。因为数组中元素是不重复的，所以我们可以先用“二分查找”找到旋转中心的位置如p，然后我们可以比较nums[p]、nums[-1]与target的大小，若target在nums[p]到nums[-1]之间，则在数组的后半部分进行“二分查找”，否则在前半部分进行“二分查找”，总的时间复杂度为O(nlogn)，beat 100%。

79.（81:Medium）（非常经典题）Search in Rotated Sorted Array II

• 该题的元素在数组中会出现重复，也就是说，我们不能再用二分查找的思路来寻找旋转中心，因为若当nums[mid]=nums[high]时，指针不知道该如何移动，如nums=[2,2,2,0,2,2]。所以，一种方法就是从头至尾遍历，若nums[i]>nums[i+1]，则i+1的位置就是旋转中心，这样会把时间复杂度增加到O(n)，只能beat 58%的人。
• 一种O(nlogn)的方法如下，参考链接：O(nlogn)二分法解决重复元素问题

   1) everytime check if targe == nums[mid], if so, we find it.
   2) otherwise, we check if the first half is in order (i.e. nums[left]<=nums[mid]) and if so, go to step 
      3), otherwise, the second half is in order,   go to step 4)
   3) check if target in the range of [left, mid-1] (i.e. nums[left]<=target < nums[mid]), if so, do search 
      in the first half, i.e. right = mid-1; otherwise, search in the second half left = mid+1;
   4) check if target in the range of [mid+1, right] (i.e. nums[mid]<target <= nums[right]), if so, do 
      search in the second half, i.e. left = mid+1; otherwise search in the first half right = mid-1;

   The only difference is that due to the existence of duplicates, we can have nums[left] == nums[mid] and 
   in that case, the first half could be out of order (i.e. NOT in the ascending order, e.g. [3 1 2 3 3 3 
   3]) and we have to deal this case separately. In that case, it is guaranteed that nums[right] also equals 
   to nums[mid], so what we can do is to check if nums[mid]== nums[left] == nums[right] before the original 
   logic, and if so, we can move left and right both towards the middle by 1. and repeat.

• 可以参考第98题（154）的方法来找旋转中心

80.（713:Medium）（非常经典题）Subarray Product Less Than K

• 该题是自己第一次分析题干信息，得出应该用“双指针”思路解决问题的题目，原因是：符合条件的子数组是“连续的”，而不是“跳跃的”，跳跃的子数组只能使用DFS来解决，而连续的子数组不仅能用DFS暴力解决，同时DFS也可以转化成for循环，鉴于第69题（11）的分析总结，该题的最佳方法应该是使用“双指针解法”。
• 虽然意识到了“双指针解法”，但解决的思路并不是完美的，在测试test case的过程中，当nums的长度过长（大于1000）时，会提示递归深度溢出，但思路确实正确的。接下来我把思路（双指针+递归）简述如下：以nums = [10, 5, 2, 6], k = 100为例，开始设置两个指针left、right分别指向数组的最左端和最右端，并求出left和right所夹所有元素的乘积product，若product>=k，则比较nums[left]、nums[right]的值，假如nums[right]较大，则我们接下来递归left...right-1的部分，而剩余的部分right，因为可能出现nums[x]..numsright满足乘积小于k的条件，所以我们需要额外处理剩余部分，即从right开始往左数，看看是否有以nums[right]结尾的子数组满足条件，并记录个数，每次递归都按此思路。当某一层的nums[left]...nums[right]整个子数组的product<k时，我们发现，该子数组中满足条件的子数组个数为(设length=left-right+1)：(length+1)*length/2。这样只要递归到满足条件的子数组时停止即可，最后返回总的个数。
• 其实上面的解法虽然使用到了双指针，但并没有完全抛弃DFS，仍然使用到了递归。虽然认识到了当某段数组的乘积小于k，其内满足条件子数组个数为(length+1)*length/2，但并没有将该性质“活用”，真正的双指针解法（完全抛弃递归）如下：
• 1.我们总是维护一个窗口中子数组元素的积小于k的长度可变的窗口（滑动窗口），并使用指针i、j分别指向滑动窗口的两侧作为边界，初始时刻i=j=0，每次我们将j向右移动一个单位增加一个新的数字到窗口中（product *= nums[j]）并计算新窗口的积。当新窗口的积大于k时，我们将左侧的i指针向右移动，即，使当前的product更新为product/nums[i]直到i、j所夹的数组的积满足product<k的条件（窗口的大小可以为空）；当积小于k时，我们在总的个数上加“当前窗口的大小j-i+1”，即以nums[j]为尾的满足条件的子数组个数。
• 下面的思路更简洁清楚：

/*
    The idea is always keep an max-product-window less than K;
    Every time shift window by adding a new number on the right(j), if the product is greater than k, 
     then try to reduce numbers on the left(i), until the subarray product fit less than k again, 
      (subarray could be empty);
    Each step introduces x new subarrays, where x is the size of the current window (j + 1 - i);
    example:
    for window (5, 2), when 6 is introduced, it add 3 new subarray: (5, (2, (6)))

    */
    public int numSubarrayProductLessThanK(int[] nums, int k) {  //数组中的元素值均大于0，维护一个小于K的最大积窗口
        if (k == 0) return 0;
        int cnt = 0;
        int pro = 1;
        for (int i = 0, j = 0; j < nums.length; j++) {
            pro *= nums[j];
            while (i <= j && pro >= k) {
                pro /= nums[i++];
            }
            cnt += j - i + 1;
        }
        return cnt;        
    }

81.（63:Medium）Unique Paths II

• 该题与第51题（62）的题目类似，解法也类似，只需要O(n)的额外空间复杂度即可解决问题。唯一不同的地方是，当我们遍历的obstacleGrid[i][j]为1时，证明该处有障碍物，于是应将row[j]的对应位置设为0表示没有一条路径可以到达此处。在处理第一行与第一列元素时，也要遵循物体只能从上侧或左侧到来，而不能一味的全部设为1，为了防止第一行与第一列中也可能有障碍物。

82.（209:Medium）Minimum Size Subarray Sum

• 该题与第80题（713）类似，只不过乘积换成了和，也是设立两个i、j指针（双指针法）分别代表可变滑动窗口的两个左右边界。当窗口中的和小于s时，则j指针右移添加新的元素到窗口中，直到sum>s，此时先比较当前长度和最短长度并将最短长度值更新，然后i指针右移，将窗口左侧的元素剔除直到sum<k，此时j指针再右移添加新元素到窗口中，如此循环直到j=len(nums)-1。总的时间复杂度为O(n)。
• 该题还有O(nlogn)时间复杂度的解决方法，凡是时间复杂度中出现logn的，一般都会运用“binary search”、“divide and conquer”等二分的技巧。

该题O(nlogn)的解法没有学习，等下次复习时再研究

83.（228:Medium）Summary Ranges

• 该题不知道要考察哪方面的知识，只需要比较相邻元素即可，若相邻元素差1则说明范围还可以扩大，否则以当前元素为止作为当前范围的截止点。

84.（56:Medium）Merge Intervals

• 该题用空间换取时间，如果在intervals列表内原地in-place处理，会很麻烦，所以应开辟一个新的列表来存储合并的区间。因为intervals列表中的元素是Interval类，所以为了方便处理，我们应该对类进行排序，需要自己定义排序规则。对于Python，我们可以使用cmpfun = operator.attrgetter("start") #按类对象的start属性值大小排序； intervals.sort(key = cmpfun)；两个语句指定sort排序时元素比较的基准。之后我们用两个指针i、j分别指向intervals列表、returnedIntervals列表，当returnedIntervals[j].end < intervals[i].start时，说明两个区域不想交，此时应将intervals[i]加入returnedIntervals列表中，i、j指针同时后移；当returnedIntervals[j].end < intervals[i].end时，应更新returnedIntervals[j].end=intervals[i].end，同时i指针后移，j指针不动，若returnedIntervals[j].end > intervals[i].end时，只后移i指针即可，其他不做改变。注意，因为我们已经将intervals的列表元素按照start属性排序，所以后面元素的start属性一定大于前面的，故无需再做比较。

<85>.（16:Medium）（非常经典题）3Sum Closest

• 该题一拿到手，也是最先想到的就是三层for循环或者深度为3的DFS来暴力求解，无需尝试，这种粗暴的方法一定是超时的。那么根据之前第69题（11）后的分析总结，我们一定可以将“三层的for循环”使用“指针法”来代替，那么用几个指针呢？因为是三层for，所以一定需要使用三个指针。
• 受到第59题（611）的启发，我们将一个指针right2设在最右侧，另外两个指针left、right1设置在以最右侧指针为界限的一头一尾的位置。因为我们共有三个指针，若同时移动三个指针，会发现逻辑非常的混乱，有一种用for循环暴力解决的冲动，因此，合理的办法是，在将最右侧right2指针设置不动的情况下，只移动left、right1指针到合适位置，即，当sum<target时left右移，sum>target时right1左移，sum=target时直接返回，该次循环耗时O(n)；然后再将right2左移一个单位，left初始化为0，right1初始化为right2-1，继续新的循环。因为right2移动的时间复杂度为O(n)，而每一层的时间复杂度为O(n)，所以总的时间复杂度为O(n^2)。在每层循环的过程中，均比较记录最小误差时left、right1、right2的坐标位置，最后在跳出总的循环时，返回三个位置的元素和即可。

86.（34:Medium）（经典题）Search for a Range

• 题目中说到要用O(logn)时间复杂度的数量家解决问题，无疑需要使用二分查找的方法。但当元素有重复时，我们无法确定二分查找的结果是重复值中的哪一个，如nums=[1,2,4,4,4,4,5]，我们不能确定找到的target的数组下表是在四个4的中间还是开头起始位置，所以，我们不仅每次要比较nums[mid]与target的大小，还要比较nums[low]、nums[high]和target的比较，即当nums[mid]=target时，我们判断nums[low]、nums[high]是否与target相等，若均相等，说明low、high指向的就是4的首末位置，直接返回即可，否则，需要将相应的low+1、high-1。while循环的退出条件为nums[low]<nums[high]而不是low<high，这不仅包括了当low=high时，两个指针值相等可以退出循环，而且当low!=high，nums[low]=nums[high]=target时也可以退出循环，一举两得。因此，在while循环后，我们需要判断nums[low]与target是否相等， 若相等则说明low、high指向的是target的首末位置，否则说明low=high且与target不等从而被迫退出while循环，此时应返回[-1,-1]。

该题上面的方法只beat了5%的人，因为每次循环过程中，可能还存在着low、high指针的移动，所以效率较低。此外，还有更高效的“左右边界法”，但没有研究，可参看discuss票数最高的帖子，需要下次复习时学习。

• 正确的思路是，先找target的左边界，再找target的右边界，使用两次binary search，可参考代码如下：

    public int[] searchRange(int[] nums, int target) {
        int[] res = new int[]{-1,-1};
        
        if(nums == null || nums.length == 0)
            return res;
        
        int left = 0, right = nums.length - 1;
        //寻找左边界
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        if (nums[right] != target) return res;  //target在nums数组中不存在
        res[0] = right;
        
        //不用reset left的值为0
        right = nums.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] <= target) left = mid + 1;  //左边界总是向右倾斜
            else right= mid;
        }
        res[1] = left - 1;  //left其实指向的是target最后一次出现的后一个位置
        return res;
    }

87.（775:Medium）（经典题）Global and Local Inversions

• 这道题的global inversions是在斯坦福大学算法课关于divide and conquer一节中讲解到的，我们可以使用merge sort的过程来统计global inversions的数量，当merge两个已排序好的数组时，用i指针指向第一个数组nums1=[start,mid]，j指针指向第二个数组nums2=[mid+1, end]，若nums1[i]<=nums2[j]，那么说明没有inversions；当nums1[i]>nums2[j]时，说明nums2[j]应排到nums1[i...mid]共mid-i+1个数之前，所以需要在countOfGlobalInversions上加mid-i+1。对于local inversions，我们可以在merge sort前从头到尾遍历比较A[i]与A[i+1]的大小，进行统计即可。统计local inversions数量的时间复杂度为O(n)，统计global inversions数量的时间复杂度为O(nlogn)，所以该方法总的时间复杂度为O(nlogn)。（只beat 2%）
• 另一种方法：因为题目只要求我们返回Ture或False，并不需要给出具体的inversions的数值，即省去了上面方法的统计步骤，所以我们只需要判定某一时刻global inversions大于local inversions即可。因为每一个local inversions都是global inversions，所以如果“local inversions=global inversions”，我们可以理解为，A数组中只有local inversions。那么如果A中只有local inversions，如果将所有local inversions排序后，整个A就会是顺序的。如果A中存在global inversions，那么即使将local inversions都全部排序，A仍然不是有序的。（该方法的时间复杂度为O(n)，beat 45%）。参考链接：O(n)检查数组中是否全是local inversions

88.（55:Medium）（非常经典题）Jump Game

• 该题最容易想到的方法是使用DFS，尝试有没有可能的路径能跳到数组的末尾，但可惜该方法超时。
• 贪心算法思想(beat 97%)：在数组的每一个位置记录一个最大可以到达的距离maxLocation，并每次在移动指针后将其更新。如果每次最大可达距离maxLocation小于当前位置可达的最大距离，则将其更新否则不变。若某一时刻，数组的指针i超过了maxLocation，说明从开始位置是无法到达位置i的，此时应直接返回False，否则在while循环遍历整个数组后返回True。参考链接：Simplest O(N) solution with constant space

通过该题，意识到应该学习一下“贪心算法”

89.（31:Medium）（经典题）Next Permutation

• 一开始没有理解题意，后来发现，该问题其实考察的是排列组合的知识。字典序可以看做是数学中的排列组合，比如“1，2，3”的全排列，依次是：

   1 2 3
   1 3 2
   2 1 3
   2 3 1
   3 1 2
   3 2 1

• 所以题目的意思是：从上面的某一行重排到其下一行，如果已经是最后一行了，则重排成第一行。至于如何求下一个全排列，举例如下：nums=[6,5,4,8,7,5,1] 从后往前看，发现8、7、5、1是递减的，从4开始才打破该规律，那么我们需要做的是从8、7、5、1中选取恰好大于4的数且离4的值最近的数，即5，然后我们将其交换后nums=[6,5,5,8,7,4,1]，接着，我们需要将8、7、4、1升序排列，最后的结果就是答案。
• 因为题目要求我们in-place排序，且不能分配额外空间，这就要求我们只能做最基本的“交换操作”，上网查阅后发现有原地归并排序，实现较复杂，其实本题也不需要使用该排序算法，因为我们发现有如下性质：原来8、7、5、1是降序的，若从后往前寻找第一个恰好大于4的数，并将其交换，那么交换后的序列仍然是“降序的”，所以，我们只需要设立两个指针p、q（其实一个指针即可）分别指向序列的头尾位置，两两交换后并做p++、q--操作（相当于关于中点做镜像对称），最终的序列就是升序的。时间复杂度为O(n)，beat 67%。

90.（229:Medium）（非常经典题）Majority Element II

• 第一种方法是维护一个字典，存储每个元素出现的次数，第一次遍历数组nums即可统计出全部元素的频度，第二次遍历字典，返回出现次数大于⌊n/3⌋的元素即可。使用了O(k)的空间复杂度，O(n)的时间复杂度（beat 85%）。
• 其实上面的方法并不严格正确，且一般意义上适用于任何该类型的题目。其实，题目中要求majority的出现次数要大于⌊n/3⌋，隐含说明了：如果存在符合条件的majority elements，它的个数“最多”为2，即若有两个出现次数大于n/3的元素，那么剩余的元素最多只能出现小于n/3次。另外，我们需要借用“Moore majority vote algorithm(摩尔投票算法)”的思想（第28题（169）Majority Element就完全使用了该算法思想），原本的摩尔投票算法是寻找出现次数大于n/2的元素，因为这里是大于n/3，所以我们需要设立两个candidate变量和两个count计数器，四个变量全部初始化为0。在第二轮循环确认两个candidate变量确实满足条件时，我们需要用set变量去重，防止candidate1=candidate2。

参考链接：

使用Boyer-Moore Majority Vote algorithm解决Majority Element II

Majority Voting Algorithm 解析（推荐）

91.（79:Medium）Word Search

• 该题无法使用for循环，因为实在没法解决，那么在不能使用for循环的情况下使用DFS，或许可以通过OJ，事实也的确如此。另一方面，该题有点像迷宫题，也确实是一个应该使用DFS深度优先搜索遍历来解决的问题。
• 在使用DFS试探的过程中，有几个注意点：1、因为board中可能不同位置存在相同的字母，所以我们需要遍历所有的board元素，当某元素与word的第一个字符相等时，则以当前元素为起始点开始DFS。 2、因为在遍历过程中，任何一个位置上的元素不能用两次，所以在进入DFS函数的第一步操作，就是将当前位置的元素置0。 3、我们在每一层DFS试探的过程中，遵循“向上->向右->向下->向左”的顺序进行路径的试探。 4、不能否认，在以某一个位置为起始点时，我们试探的任何路径可能都不成功，但因为在DFS函数的开始我们已标记当前位置为“已遍历”（置0），所以在该层“上下左右”四个方向路径全部搜索失败后，在向上层返回False前，需要先将该位置的值恢复（可以在置0前用一个临时变量将其存储），因此，我们也不需要用到列表的深度拷贝，从而才能大大缩小时间，通过OJ（beat 98%）。

92.（18:Medium）4Sum

• 该题与第85题（16）一样，在暴力方法均可以使用四层嵌套的for循环，或者深度为4的DFS的情况下，我们使用“4指针解法”(注意n指针法的使用前提为数组是有序的)，将时间复杂度从O(n^4)降为O(n^3),相当于嵌套的三层for循环。四个指针p1、p2、p3、p4的初始时刻为，p1=0，p4=len(nums)-1，p3=p4-1，p2=p3-1。在指针移动过程中，最外层是p4，次外层是p3，最内层是p1、p2。（只beat 26%）

该题还有其他更高效的解法，基于2Sum等，在下次复习时需要再研究学习

93.（15:Medium）（经典题）3Sum

• 该题与第85题（16）、第92题（18）都是同类型的题，在该题中，我们只需按上题的思路设立三个指针，在O(n^2)的时间复杂内即可解决问题。
• 需要注意的是，数组中的元素可能是duplicate的，一种方法当然是在每次向返回的列表中添加成员的时候，使用not in来判断是否有重复；另一种方法是，每次移动指针时，用while循环来判断相邻的两个元素是否相同，若相同则继续移动指针，直到移动到不相同的元素上。用第二种方法的时间效率远高于第一种（第二种beat 78%，第一种无法通过OJ），而把第二种方法应用到第92题（18）中作改进，可以提高到beat 32%。

94.（152:Medium）（经典题）Maximum Product Subarray

• 该题受到第60题（560）的启发，我们建立一个product变量来存储nums[0]...nums[i]的所有元素的积，同第60题的思路一样，任意连续子数组的积为product/product'的值（product指到i位置为止的积，而product'代表到i之前某个位置j为止的积,i>j）。但因为该题不要求统计个数，所以我们没有必要建立字典、列表等存储所有位置的product。考虑到乘积运算的性质，要求最大积，对于正数：我们只需要让product除以一个i以前的最小的正数积即可；对于负数：我们只需要让product除以一个i以前的最大的负数积即可。这样，每当我们求得i位置的product值并且比较完到当前位置为止的maxProduct后，都要根据当前product的值更新minPlusValue最小正数积值和maxMinusValue最大负数积值。需要注意，在初始化时，minPlusValue可以初始化为系统的最大正数，因为任何一个正数除以最大数都是0，一定小于该正数积；而maxMinusValue要初始化为1，因为任意负数除以系统内置的最小负数结果都是0，0是大于当前的负数积的，显然不符合条件，所以，当maxMinusValue=1时，若product<0，我们直接将maxMinusValue赋值为product，在之后的比较中，才按照product>maxMinusValue的判断条件来更新该值。
• 在输入的数组中，有可能还有0的元素，这样在计算product时，0元素及其之后的位置积均为0，这就要求我们在遇到0元素后，从0元素之后的位置重新初始化product(=1)、minPlusValue(=系统最大正数)、maxMinusValue(=1)，相当于以0元素为分界线将数组截断成两部分，但maxProduct值维持不变。需要注意的是，当product=0时（此时nums[i]=0）,仍然需要与maxProduct进行比较，因为maxProduct可能小于0，而对前面三个变量的重新初始化操作应在maxProduct值比较更新完后执行。（以上思路beat 99.4%，时间复杂度仅为O(n)，空间复杂度为O(1)）

95.（768:Hard）（经典题）Max Chunks To Make Sorted II

• 该题与第44题（769）的思路类似，只是在求position数组的偏移位置时有所区别，后面基于position数组来找最大的chunk数量的方法是相同的。
• 因为该题的元素值并不是在[0,1,...,arr.length-1]，而是在[0, 10^8]，所以我们不能保证当元素的值为val时，排序后就应该放置在val位置上，所以，为了确定元素排序后的位置，我们只能对输入的数组arr进行排序。因为我们要记录每个元素排序后的位置，最快捷最高效的方法就是使用字典dict，键值为数组中的元素，对应的值为一个列表（考虑到会有重复元素），列表中存储的是该元素在排序后数组中的各个位置。那么，在计算输入数组arr的元素的移动距离时，对应的偏移量为dict[val][0] - i（i为当前元素在arr数组中的位置，val为当前元素值），即取出字典中对应数据值列表的第一个元素，计算完成后，需要将第一个值删除，dict[val].pop(0)，表示相同元素的第一个目标位置已经被占用，应使用下一个目标位置。完成了position数组之后，后续的思路可以参照第44题（769），剩余的部分没有什么区别，在此不再赘述。（该方法beat 74%）

该题可能还有其他高效的方法，做题时并没有看discuss的讨论，下次复习时需要研究学习

• 一种高效的解题思路：

    /*
    Algorithm: Iterate through the array, each time all elements to the left are smaller (or equal) to all elements to the right, there is a new chunck.
    Use two arrays to store the left max and right min to achieve O(n) time complexity. Space complexity is O(n) too.
    This algorithm can be used to solve ver1 too.
    */
    public int maxChunksToSorted(int[] arr) {
        int n = arr.length;
        int[] maxOfLeft = new int[n];
        int[] minOfRight = new int[n];

        maxOfLeft[0] = arr[0];
        for (int i = 1; i < n; i++) {
            maxOfLeft[i] = Math.max(maxOfLeft[i-1], arr[i]);
        }

        minOfRight[n - 1] = arr[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            minOfRight[i] = Math.min(minOfRight[i + 1], arr[i]);
        }

        int res = 0;
        for (int i = 0; i < n - 1; i++) {
            if (maxOfLeft[i] <= minOfRight[i + 1]) res++;  //比较相邻的maxOfLeft和minOfRight，如果左面最大的元素要比右边最小的元素还大，说明这个chunk应该继续向右延伸;否则说明当前的排序已经是满足升序的，可以进行切割
        }

        return res + 1;
    }

96.（128:Hard）（经典题）Longest Consecutive Sequence

• 这道题虽是hard题目，但其实解决起来并不困难，我们只需要解决“两个问题”即可。
• 第一个问题：因为我们想要找到元素值连续的最长长度，所以我们应该尽量从这个序列的最小值开始找起，那么怎样找最小值呢？一种方法是用for循环，另一种方法是用min()函数。for循环的方法不可取，因为数组中可能存在多个值连续的序列，那么每找一个序列的值，我们就需要遍历一次数组，这显然是非常粗暴的、没有技巧的方法。但如果使用min()函数，我们能取到当前数组的最小值没错，但是每次取到的最小值都是序列的最小值，因此，我们需要在搜索一个序列值时，将已搜索的值改为系统的最大值作为已经遍历过的标志，这样，每次搜索完一个序列，当下次使用min()函数时，获取的是另外一个不同序列的最小值。
• 第二个问题：数组中的元素时unsorted的，那么我们如果要判断连续的值是否存在，又要在O(n)时间复杂度内解决问题，肯定不能使用for循环，那么如何才能做到一次存取即可判断当前元素的相邻值是否存在呢？使用字典的数据结构无疑是唯一且正确的选择。建立字典的结构只需要一次遍历O(n)时间复杂度内即可完成，我们将元素的值作为键，将元素的下标作为对应的值（为了方便修改已遍历元素的值为系统最大值）。因为数组中可能出现重复的元素，但重复元素其实对我们该题的解决不会产生什么影响，因为相同的值我们只会搜索一次，因而在建立字典的过程中，若nums数组的某元素的值重复出现，则直接将对应位置的值改为系统最大值即可。
• 解决了以上两个问题，我们便可以在O(n)时间复杂度内求解，空间复杂度为O(n)，相比于for循环的空间复杂度使用情况，上面的解法相当于牺牲了空间换取了时间。（beat 61.7%）
• 上面的思路是在Python下的，对Java不适用，以下是java的其中一个可行的O(n)时间复杂度的实现思想：这道题要求求最长连续序列，并给定了O(n)复杂度限制，我们的思路是，使用一个集合set存入所有的数字，然后遍历数组中的每个数字，如果其在集合中存在，那么将其移除，然后分别用两个变量pre和next算出其前一个数跟后一个数，然后在集合中循环查找，如果pre在集合中，那么将pre移除集合，然后pre再自减1，直至pre不在集合之中，对next采用同样的方法，那么next-pre-1就是当前数字的最长连续序列，更新res即可。

    public int longestConsecutive(int[] nums) {
        int res = 0;
        Set<Integer> s = new HashSet<Integer>();
        for (int num : nums) s.add(num);
        for (int num : nums) {
            if (s.remove(num)) {
                int pre = num - 1, next = num + 1;
                while (s.remove(pre)) --pre;
                while (s.remove(next)) ++next;
                res = Math.max(res, next - pre - 1);
            }
        }
        return res;
    }

并没有参看discuss的思路解法，所以下次复习时可以研究学习一下

<97>.（689:Hard）（非常经典题）Maximum Sum of 3 Non-Overlapping Subarrays

• 该题一开始想到的思路是：求出到nums数组中位置i及以前所有元素的和，那么nums[x]...nums[y]之间所有元素的和为sum[y]-sum[x-1]，这样，知道了k，我们只需要按照sum[i]-sum[i-k+1]的运算方式，便可以在一次for循环的时间复杂度找出一个和最大的子数组的起始位置，之后，将该数组的对应k个位置设为0（标记为已使用），再重新计算sum数组，这样循环3次每次找出一个最大的子数组便得到了答案。但是，该方法不能保证Non-Overlapping，即假如一次循环后的数组为nums'=[1,2,0,0,2,8],k=3,第二次取得的最大数组一定是[0,2,8]，但是i=3位置的元素已经被使用过了，于是出现了overlapping的现象。
• 后来为了满足Non-Overlapping的条件，想到该题其实可以看做另类的三指针问题，只是此处的指针是长度为k的三个子数组而不是单个的元素，那么按照三指针的思路，我们仍然计算sum数组，三个代表子数组起始位置的指针p1、p2、p3初始化为一个头两个尾并且p3-p2>=k，但问题是，当我们计算出当前三个数组的和之后，p3、p2应该怎样移动呢？是移动p1还是移动p2？回想以前的多指针问题，数组中的元素是升序排列的，且存在一个target作为比较，但该题并没有tartget且数组中元素乱序，所以无法使用该思想。
• 最后，参看Discuss和Solution，该题被定为是DP问题。我们用i、j、q三个指针表示可能满足条件的三个数组的起始位置，假如“固定”j不动，那么在[0,j-k]区间和[j+k,len(nums)-k]内，我们需要寻找和最大的子数组下标i、q。我们可以用“动态规划DP”解决该问题，首先仍然用一个数组W存储从[0,len(nums)-k]为止的长度为k的子数组元素之“和”（例如k=2，那么W[0]=nums[0]+nums[1]）。接着我们建立两个列表数组left、right，left[i]表示在[0,i]中，子数组元素和最大的数组起始索引，而left[i]表示在[i,len(nums)-k]中，子数组元素和最大的数组起始索引。需要注意的是，当我们知道left[m]的值要求left[m+1]的值时，只需要比较W[left[m]]和W[m+1]的值即可，例如我们知道[0,5]中，最大的子数组起始位置为2，那么left[5]=2，现在要计算left[6]，只需要比较W[6]和W[2]的值即可，若W[6]较大，那么left[6]=6否则left[6]=2（我认为该处使用了动态规划的思想，不能确定）。right数组同理。那么在求出right和left数组后，我们便将j指针在[k,len(nums)-2*k+1]的范围内进行移动，当j在某位置时，left[j-k]、right[j+k]便是在j处于当前位置的前提下，三个最大的子数组起始索引。我们只需要用一个变量maxSum来存储已经遍历过得j的位置下最大的和，之后j每到一个新位置，只需要将新的和与之前的和比较，取较大者并更新三个指针的位置记录即可。（beat 65%）

该题不确定在何处使用了DP思想，且discuss中的思路没有完全看懂，上面阐述的思想是solution中的方法，下次复习时需要与别的同学探讨学习。且需要学习DP的相关知识

98.（154:Hard）（非常经典题）Find Minimum in Rotated Sorted Array II

• 该题是第56题（153）的变种，在第56题中，每个元素都不相同，所以不会出现nums[mid]=nums[high]的情况。在该题中，我们需要认识到，当nums[mid]!=nums[high]时，指针的处理方式应该与第56题中一样，关键是，当nums[mid]=nums[high]时，low和high指针应该怎样移动。
• 因为我们要找的是最小的元素，或者说是旋转的中心，因此，当nums[mid]=nums[high]时，我们可能会想到继续比较nums[mid]和nums[low]的大小，但是当nums[mid]=nums[high]时，因为我们不知道最小元素的位置，所以我们其实可以从“两方面”来考虑：1、假设nums[mid]=nums[high]="最小值"，此时我们其实只要保留mid或high其中一个在我们继续扫描的范围内即可，这样我们一定能最终定位到最小值上 2、假设mid、high位置都不是最小值，那么最小值可能在[low,mid]之间，或[mid,high-1]之间，或总之是在[low,high-1]之间。 那么综上，我们只需要在nums[mid]=nums[high]成立时将high-1即可，重新计算mid的位置。当nums[mid]!=nums[high]时，处理方式同56题相同。

99.（42:Hard）（经典题）Trapping Rain Water

• 观察下就可以发现被水填满后的形状是先升后降的塔形，因此，先遍历一遍找到塔顶，然后分别从两边开始，往塔顶所在位置遍历，水位只会增高不会减小，且一直和最近遇到的最大高度持平，这样知道了实时水位，就可以边遍历边计算面积。换句话说，我们使用两个for循环，一个用来计算塔顶左侧的水量，一个计算塔顶右侧的水量。（beat 97%）
• 按自己的思路研究了半天，一直只关注给的高度的变化，并没有全局的看水填满后的形状，以后应转换角度思考问题。

该题的tag为双指针，正如上面的说法，两个for循环确实是一左一右向塔顶逼近，而该题明显比之前的双指针问题更偏生活化更形象。同时该题也是stack类型题，没有搞懂，可能还有其他类型的解法，下次复习时需要再研究学习。

100.（782:Hard）Transform to Chessboard ？？？？？

• 并没有完全理解该道题的实现，参考的实现代码：实现代码及思想
• 现在将上面链接中的内容简单复述如下：

   两个条件可以帮助我们解决该问题：
   1、在一个有效的chess board中, 只会存在两种情况的行，即一种是另一种的异或。对于列也有同样的性质。
      例如：假如某行是01010011，那么其他的行一定是01010011或10101100。
      由上面的性质得出的“推论”是：在board中任意的取一个长方形，这个长方形的左上角、右上角、左下角和右下角一定是“4个0”、“2个0，2个1”、“4个1”其中的一种。
   2、另一个“性质”是，每一行和每一列有一半的1，假设board是N*N的：
      如果N=2*K(偶数)，每一行和每一列有k个0、k个1
      如果N=2*K+1(奇数)，每一行和每一列有“K+1个0和K个1”或“K+1个1和K个0”
      对于一个给定的有效的board，“交换”不会打破这个特性，这个性质一定存在。

• 一旦我们知道它是一个有效的board，我们就开始计算交换的次数。基于上面提到的特性，当我们处理第一行的时候，我们实际上也移动了所有的列。

   例如：尝试将某一行处理成01010和10101，计数交换的次数
   1、假设N是偶数，我取最小的交换次数，因为两者都是可能的
   2、假设N是奇数，我取偶数次的交换
      因为当我们做交换时，我们同时移动两行或两列，所以列的交换或行的交换应该是偶数次的。

该题并没有搞懂，也并没有进行实现，需要再次复习时与同学一起讨论，

101.（715:Hard）（非常经典题）Range Module

• 该题与第68题（731）的思路很像，同样都是区间操作，只是在其基础上又增加了删除的操作。该题分为三个操作，我们分别进行讲解。
• “增加”区间：增加区间的一个关键是“如何判断新增加的区间与旧区间有重合”和“若有重合应该如何进行不同区间的合并”。第一个问题在第68题（731）的实现思路中已经给了很好的答案，假设我们新增加的区间为[left,right)，旧区间为[oldLeft,oldRight)，当left<oldRight且right>oldLeft时，两个区间存在交叉重叠部分。那如何解决第二个问题呢？一种方式为，我们在旧区间的基础上将其首末界限进行修改，但问题是，当旧区间有两个[[5,7),[8,10)]，若增加新区间[7,8)，当搜索到第一个区间时，我们很容易将其改为[5,8)，但是，若再将[5,8)与[8,10)进行合并，这个过程或者类似过程的处理是非常麻烦的，且很可能存在逻辑疏漏导致情况处理不完备而出错。这里的采用的方法是，不修改原来的旧区间，而是修改输入的新区间，同时将与其重叠的和与其相邻的旧区间进行记录。例如原区间为[[5,7),[8,10)]，输入新区间为[6,8)，当搜索到第一个区间时，因为有重叠，那么我们将[6,8)扩充为[5,8)即对两个区间的范围求“并集”，而搜索到第二个集合时，因为[5,8)与[8,10)相邻，那么我们将两集合拼接得到[5,10)。遍历结束后，我们通过remove方法统一对“与输入的新区间有重叠”或“相邻的”旧区间进行删除，删除结束后再用append方法将“更新后的”新区间加入到Intervals数组中。这里最后“统一”使用“remove方法”而不是“pop方法的”原因是：(1)当每遍历完一个旧区间就进行删除可能会因后续元素索引下标的减少而导致元素访问的跳跃 (2)如果我们是通过索引来记录重合旧区间的位置，那么在用pop删除的过程中，实际索引是会变化的，与记录的索引位置可能不同。
• “寻找”区间：该操作较易实现，只需要遍历已存在区间，并寻找是否有旧区间能够**“完全包含”**输入区间即可。
• “删除”区间：删除区间的操作也涉及到一个区间重合的问题。而“删除”操作恰恰与“增加”操作效果相反，可能需要旧区间的“分裂”。这里的思想与增加操作的思想相似，将我们首先计算出重叠的区间范围，然后去与旧区间进行比对，从而得到未重叠的旧子区间范围，对于这些未重叠的旧子区间，我们将其进行记录，而对有重叠的旧区间我们同样也进行记录。将所有旧区间遍历完后，我们会将有重叠的旧区间，“整块”删除。虽然这些旧区间从头至尾全部被删除，但它们中所含的未重叠部分我们已做记录，只需要将他们全部删除完后，再append未重叠部分即可。
• 该题的难度主要在于，对区间进行合并与分解时的处理，一开始我拘泥于对单个区间的范围进行扩展缩减操作，首先是逻辑混乱复杂，其次没有考虑其他区间的范围与之前变换后的新区间范围的联系，故是错误的。所以，应从大局观来观察问题解决问题。此外，该题没有采用第68题（731）中对重合区间或已删除区间单独开辟新数组进行存储记录的原因是，题干中允许这样的操作“remove([8,9)),add([8,9))”，这样的话，在已删除区间数组中记录了[8,9)是已经删除掉的，但实际的区间中确实存在[8,9)的范围，所以第68题的方法在此处行不通。

更高效的解决方法请参看Java版本的实现代码

上面的方法耗时很长，只超过了1%，下次复习时应该参看discuss中更优质的答案

<102>.（123:Hard）（非常经典题）Best Time to Buy and Sell Stock III

• 该题和之前的Best Time to Buy and Sell Stock I、Best Time to Buy and Sell Stock II是同一系列的问题，即均需要使用动态规划DP思想来进行解决。但与Best Time to Buy and Sell Stock II不同，我们在这里不能使用相同的思路，即在效益降低时存储当前时刻的最大时间，或者说Best Time to Buy and Sell Stock II的解题思路没有抓住问题的本质，不能适用于所有该类问题的求解。
• 通用的思路如下（参考网上帖子）：仍然使用动态规划来完成，事实上可以解决非常通用的情况，也就是最多进行k次交易的情况。这里我们先解释最多可以进行k次交易的算法，然后最多进行两次我们只需要把k取成2即可。我们还是使用“局部最优和全局最优解法”。我们维护两种量，一个是当前到达第i天可以最多进行j次交易，最好的利润是多少（global[i][j]），另一个是当前到达第i天，最多可进行j次交易，并且最后一次交易在当天卖出的最好的利润是多少（local[i][j]）。个人理解，这里的“交易”是指在第i天有一次卖出，并不一定在同一天必须买入。
• 下面我们来看递推式，全局变量的比较简单：global[i][j]=max(local[i][j],global[i-1][j])，也就是取当前局部最好的，和过往全局最好的中大的那个（因为最后一次交易如果包含当前天一定在局部最好的里面，否则一定在过往全局最优的里面）。对于局部变量的维护，递推式是local[i][j]=max(global[i-1][j-1]+max(diff,0),local[i-1][j]+diff)，这里diff=prices[i]-prices[i-1]。也就是看两个量，第一个是全局到i-1天进行j-1次交易，然后加上今天的交易，如果今天是赚钱的话（也就是前面只要j-1次交易，最后一次交易取当前天），第二个量则是取local第i-1天j次交易，然后加上今天的差值（这里因为local[i-1][j]包含第i-1天卖出的交易，如果加上diff的差值，相当于把i-1天的交易延后成第i天卖出，并不会增加交易次数，而且这里无论diff是不是大于0都一定要加上，否则就不满足local[i][j]必须在最后一天卖出的条件了）。上面的算法中对于天数需要一次扫描，而每次要对交易次数进行递推式求解，所以时间复杂度是O(n*k)，如果是最多进行两次交易，那么复杂度还是O(n)。空间上只需要维护当天数据皆可以，所以是O(k)，当k=2，则是O(1)。在实现中，需要开辟两个长度为3的数组，因为数组中1和2位置存储的是到第i天已经进行了1次或2次的交易，而0位置存储的是到第i天没有进行交易的收益，用来递推求解1位置的值，且因为没有做交易，所以0位置的值一直为0。
• 对于上面的思路，谈谈我自己的理解：1、这里我们会发现两个递推公式的右侧都会包含两种情况，即“全局/局部变量=max(全局变量情况，局部变量情况)”，所以递推的分类讨论是条件完备的。2、而且，由上面解法的思路，我们可以同一天进行多笔交易，即当天以6元买进，又在当天卖出，或者在当天以6元卖出，然后又以6元买进。实际上，因为我们手中的财务并没有变化，这样便可以转化为我们并没有在这一天进行交易，但在上面的解法中，我们仍把这种当天买卖各一次的情况“视作一次有效的交易”。3、在局部变量的递推式中，有一项为global[i-1][j-1]+max(diff,0)，其实这代表的就是一个全局的情况，因为我们要保证全局最优，global[i-1][j-1]的第j-1次交易无论是否在第i-1天交易，都没有影响，因为global[i-1][j-1]一定是到i-1天为止全局最优的，它将第i-1天的价格考虑进去，但并没有考虑第i天的价格，那么我们只需要判断i-1天到i天是否是可赚的，如果效益大于0，那我们一定会i-1天买，i天卖（由定义第i天必须有交易）；如果效益小于0，因为我们现在是对local局部变量求解，所以必须在第i天要有交易，由第2点，那么我们选择i天先买入再原价卖出，保证不违反开始的定义。
• 在实现过程中，局部变量与全局变量是交替求解的，但因为局部变量的递推式右侧只涉及i-1天的交易，而全局变量递推式右侧还涉及第i天的交易，所以在编码过程中我们先计算局部变量再计算全局变量。（上面的解法beat 60%）

上面陈述思路的链接：借助全局与局部变量的DP求解方法

• 另一种理解起来较为容易的dp思路：

1. First assume that we have no money, so buy1 means that we have to borrow money from others, we want to borrow less so that we have to make our balance as max as we can(because this is negative).

2. sell1 means we decide to sell the stock, after selling it we have price[i] money and we have to give back the money we owed, so we have price[i] - |buy1| = prices[i ] + buy1, we want to make this max.

3. buy2 means we want to buy another stock, we already have sell1 money, so after buying stock2 we have buy2 = sell1 - price[i] money left, we want more money left, so we make it max

4. sell2 means we want to sell stock2, we can have price[i] money after selling it, and we have buy2 money left before, so sell2 = buy2 + prices[i], we make this max.

5. So sell2 is the most money we can have.

public int maxProfit(int[] prices) {
    int sell1 = 0, sell2 = 0, buy1 = Integer.MIN_VALUE, buy2 = Integer.MIN_VALUE;
    for (int i = 0; i < prices.length; i++) {
	buy1 = Math.max(buy1, -prices[i]);
	sell1 = Math.max(sell1, buy1 + prices[i]);
	buy2 = Math.max(buy2, sell1 - prices[i]);
	sell2 = Math.max(sell2, buy2 + prices[i]);
    }
    return sell2;
}

该题理解起来较复杂，且discuss中还有其他的DP解法，并没有研究，在下次复习时需要再和其他同学探讨。且需要统一复习一下股票买卖问题，非常经典

<103>.（85:Hard）（非常经典题）Maximal Rectangle

• 该题根据提示的标签分类可以用很多种方法来解决，这里使用动态规划DP的思想为例作阐述(beat 84%)，其他的思想在下次复习时再研究学习。
• 使用动态规划的思想去解决这个问题，自己总结的动态规划三要素：定义概念、边界初始化、一般情况递推，两个难点是：角标索引问题、递推情况剖析。cur_left定义为在一个字符数组中，当前元素可以延伸到最左边元素的下标（当前元素为0，则这个值为0）。如在字符数组"0111001110"，对第三个1，其cur_left=1，对最后一个0，其cur_left=0。注意这里的cur_left只是和本行的0、1分布有关，与其他行的值没有关系。其示意图如下图所示（图片若不完整请参看后边的中文链接）：

• cur_right定义为在一个字符数组中，当前元素可以延伸到最右边元素的下标**+1**（当前元素为0，则这个值为字符数组的长度）。如在字符数组"0111001110"，对第四个1，其cur_right=8+1，对第一个0，其cur_right=10。注意这里的cur_right也只是和本行的0、1分布有关，与其他行的值没有关系。这里当元素值为1时，其cur_right值要**+1**，是因为我们在求矩形的下底时，根据左右边界来计算的公式为q-p+1，这里+1就用于计算上的化简，只需要求出right-left就能得出矩形的底边长。其示意图如下图所示：

• 总结：cur_left和cur_right均由当前行的值来确定。如果当前值为'1'，则cur_left和cur_right均不变，因为其记录的永远是当前位置能访问到的最左及最右侧位置，只要中间没有0则值一直保持不变；如果当前值为'0'，则cur_left值为当前元素右侧j+1（因为j位置为0，所以之后元素可能能访问到的最左侧1值的位置只能是j+1下标处），cur_right值为当前元素位置（因为cur_right永远都是最右侧的1值位置+1，所以更新后不是j-1而是j）。
• 在cur_right和cur_left的基础上，我们再结合矩形的边界形状，定义另外两个变量：**left[i][j]**定义为在第i行第j列处，包含(i,j)位置的矩形可以延伸到的最左边元素的下标。**right[i][j]**定义为在第i行第j列处，包含(i,j)位置的矩形可以延伸到的最右边元素的下标+1。
• 核心思路是从第一行开始一行一行地处理，使包含[i, j]处最大矩形的面积是(right(i, j)-left(i, j))*height(i, j)。其中height统计当前位置及往上'1'的数量；left和right是高度为当前点的height值的矩形的左右边界，即是以当前点为中心，以height为高度向两边扩散的矩形的左右边界。left、right和height的值均可以通过前一行和当前行的值来确定，因此，逐行遍历即可。递推公式如下：

   left(i,j) = max(left(i-1,j), cur_left)        #left(i-1,j)是i-1行的值，为了维持矩形的形状
   right(i,j) = min(right(i-1,j), cur_right)     #right(i-1,j)是i-1行的值，为了维持矩形的形状
   if matrix[i][j]=='1', height(i,j) = height(i-1,j) + 1;
   if matrix[i][j]=='0', height(i,j) = 0;

• 另一种思路（容易理解记忆）：This question is similar as Leetcode 84. Largest Rectangle in Histogram(单调栈)

You can maintain a row length of Integer array H recorded its height of '1's, and scan and update row by row to find out the largest rectangle of each row.

For each row, if matrix[row][i] == '1'. H[i] +=1, or reset the H[i] to zero. and accroding the algorithm of "Largest Rectangle in Histogram", to update the maximum area.

参考链接:求最大矩形：DP思路“中文”说明 DP思路“英文”说明

104.（57:Hard）（经典题）Insert Interval

• 该题实际上并不难，可以看作是第101题（715）和第84题（56）的扩展。因为在第101题和第84题中我采用了两种不同的方法来处理集合区间的变化，因此该题据此有两种解法。
• 根据第101题（715）的解法：我们采用“滚雪球”的方式扩充newInterval的左右边界，凡是与新插入区间邻接或相交叉的，我们均将这些旧区间作记录，同时扩充newInterval的左右边界。最后根据已作的记录删除这些与newInterval相邻或相交的区间，最后再append新区间即可。因为传入的列表中存储的是对象，所以不便用remove方法进行对象的删除，所以这里记录的是待删除旧区间的数组下标，为了避免删除数组中间某元素时后续待删除元素的下标发生变化，这里采用从后往前根据下标删除元素的方法。（原地in-place处理）
• 根据第84题（56）的解法：在此解法中我们不进行数组元素的删除，而是最后返回一个新的数组。那么，与第一种解法相似，我们对于完全与新插入区间newInterval不相邻或不相交的旧区间，直接添加进待返回数组中即可，而对于相邻或相交的旧区间，我们一样采用“滚雪球”的方式进行新区间左右边界的扩充。因为原旧区间是根据起始值升序排列的，那么当newInterval.end < intervals[i].start时，说明i位置及以后的所有旧区间均大于新插入区间，那么此时我们将新区间插入待返回数组的末尾，然后将i及以后的所有旧区间拼接到待返回数组即得答案。

105.（381:Hard）（经典题）Insert Delete GetRandom O(1) - Duplicates allowed

• 该题是第61题（380）的扩展，思路基本相同。因为允许插入重复元素，所以为了记录所有相同元素的位置，字典中元素键对应的值为一个列表。那么当每次进行元素的删除时，分三种情况讨论：1、待删除元素是重复的，列表最后一个元素也是重复的 2、待删除元素是唯一的，列表最后一个元素是重复的 3、待删除元素是重复的，列表最后一个元素是唯一的 4、待删除元素是唯一的，列表最后一个元素也是唯一的。 不论何种情况，我们需要遵守的规则是：当进行元素删除时，我们选择的是待删除原素最后一次出现的位置，在与最后一个位置的元素进行替换后，我们需要对原列表最后一个元素的字典值（位置列表）进行升序排列，否则会造成之后删除该元素的过程中，后面位置的数组元素下标索引减小但它们相应的字典内容未做改变，导致下标越界问题。如交换后的原列表最后一个元素的字典值(位置列表)为{x:[3,4,1]}，list数组中列表为[y,x,y,x,x]，如果不对x的字典值做升序排列，则再删除x时，会删除下标为1的x，假如与最后一个元素x作交换(实际上没有什么作用)，删除后list数组变为[y,x,y,x]，而x的字典仍为{x:[3,4]}，但实际上应为{x:[1,3]}，出现错误。

<106>.（84:Hard）（非常经典题）Largest Rectangle in Histogram

• 该题是一道ACM比赛题，又是一道Leetcode题，还是一道经常被问的面试题。该题的标准解法是利用“堆栈思想”，此外还有一些其他的解题思路，下面以堆栈思想为例进行阐述，其他方法等下次复习时再深入研究。
• 首先我们从最简单粗暴的思路开始分析：遍历所有的起始和结束位置，然后计算该区域内长方形的面积，找到最大的。具体实现过程为，从第0个位置开始遍历起点，选定起点之后，从起点到末尾都可以当做终点，所以总共有O(n^2)种可能。在固定了起点之后，后续对终点的遍历有一个特点：构成长方形的高度都不高于之前所构造长方形的高度，所以长方形的高度即是到当前终点为止的最小值，宽度即是终点位置减去起点位置加1。此方法可以通过大部分测试例，但最终会超时。
• 堆栈O(n)的解决思路为：考虑直方图两个相邻长方形AB之间的关系。如果前一个长方形A较低，后一个长方形B较高，则A肯定不会是某个大长方形的终点，因为我们可以安全地在A后面添加更高的B，使大长方形的宽度加1，而“以A为高的矩形”的总面积可以继续增大。如果A高B低，则A是可能的终点，假设我们就用A当做终点，并且以该长方形的高度当做大长方形的高度，看看可以往前延伸多长。因此，根据上面这两条性质，我们可以维护一个非递减序列，该序列中存储的是递增高度的下标索引，当B高时就将B的位置添加到序列中，否则就弹出A的索引下标，并用A的下标作为终点，A的高度作为大长方形的高度计算面积。起点怎么确定呢，由于我们维护的是一个非递减序列，在弹出A之后，序列中A的前一个位置所对应的长方形高度肯定低于或等于A的高度，所以A的前一个长方形的位置索引“加1”即是大长方形的起点（假如有序列存储的“高度”为[4,6,8,5]，我们在遍历到5的时候会将6，8出栈，而高度为5矩形的起点其实是原来高度为6的位置索引1，因其“恰好刚刚”“大于”5）。因为我们每次都是对序列的末尾进行操作，所以可以用一个栈来维护此非递减序列。（beat 74.5%）
• 下面用一个示例图形象的讲解：从第一个柱子（编号1）开始，找出所有的后一个比前一个上手的柱子（从编号1到13），直到遇到一个高度下降的柱子（编号14）。而且把下降之前的编号（从1到13）推入到一个堆栈中。然后计算栈顶编号柱子的高度（所有A1A2线之上的柱子们，从编号3到13）比下降柱子（14）高的所有矩形的面积（因为14不可能和比它高的柱子组成更大的矩形），保留最大的。从栈顶开始，比如，13，12-13，...，8-13，7-13，...，直到3-13。但是14能参与比它矮的较远的编号2（2-14，就是B1B2）和编号1（1-14，就是C1C2）组成矩形，所以编号1和2的柱子仍保留不弹出。堆栈中保留了到当前为止，所有将要参与可能矩形计算的所有柱子的编号。有了这些编号，我们可以计算所有可能的矩形的面积，从而求出最大的面积。

参考链接：“多种”方法解决最大矩形面积问题 堆栈方法的形象讲解

该题第一个链接中还有其他多种方法，下次复习时需要再仔细研究学习

107.（45:Hard）（经典题）Jump Game II

• 该题是第88题（55）的扩展，第88题中只要求判断是否能到达最后一个位置，而该题已经说明肯定能到达最后一个位置，需要给出最小的步数。
• 为了以最小步数到达最后一个位置，我们当然还是要使用贪心算法。因为我们一定能到达最后一个位置且需要求出最短步数，所以需要设立一个数组jumps来存储我们到达各个位置的最小步数，该jumps数组初始化为jumps=[0]，表示到达起始位置只需要0步。在每个位置i我们都可以求得一个能到达的最大位置，若当前可达的最大位置大于之前的maxLocation，即当nums[i]+i>maxLocation时，说明我们从当前位置以最大步数前进能到达更远的地方，那么，我们就把jumps数组添加nums[i]+i-maxLocation个元素，并将新添加的元素值设为jumps[i]+1，表明我们只需要从起点最短走jumps[i]步到达位置i，然后再多走1步即能到达“maxLocation+1”...“nums[i]+i”的各个位置，当nums[i] + i >= len(nums) - 1或len(jumps) = len(nums)时，说明我们已经找到了一条到达末尾位置的最短路径，此时只需要返回jumps[i] + 1或jumps[-1]即是满足题目条件的最小步数。（beat 77%）

该题未看discuss，可能有更好的少用额外空间的方法，下次复习时需要再研究学习

108.（41:Hard）（经典题，需看discuss）First Missing Positive

• 题目要求必须在O(n)时间复杂度内解决问题，我们当然一开始想到的是使用“哈希表字典结构”，但题目后面又提到“use constant extra space”，所以使用字典数据结构的想法是不可行的。
• 那么既然只能使用常数空间复杂度的额外空间，我们只能使用python内置的in、not in、remove、min函数，对输入的数组nums进行原地操作。思路是：首先使用min函数取当前数组中的最小值，若该最小值小于等于0，那么我们使用remove方法将其在nums数组中删除，然后再取删除后数组的最小值，重复该操作直到我们取到的最小值是一个正数为止。因为我们要获取的是第一个未出现的正数，那么就需要判断此时的正数是否为1，若不是1则直接返回1即可；若不是1，那么我们从1开始依次增加值，使用in函数判断是否在当前nums数组中，直到找到第一个未在数组中出现的正数为止。注意，在开始删除负数时，可能输入的数组本身只含负数和0，所以需要时刻判断数组是否为空，一旦为空则直接返回1即可。（beat 94%）
• 正确的思路：既然不能建立新的数组，那么我们只能覆盖原有数组，我们的思路是把1放在数组第一个位置nums[0]，2放在第二个位置nums[1]，即需要把nums[i]放在nums[nums[i] - 1]上，那么我们遍历整个数组，如果nums[i] != i + 1, 而nums[i]为整数且不大于n，另外nums[i]不等于nums[nums[i] - 1]的话，我们将两者位置调换，如果不满足上述条件直接跳过，最后我们再遍历一遍数组，如果对应位置上的数不正确则返回正确的数，

上面自己的思路可能是一个取巧的方法，并没有用到算法知识，所以下次复习时应再参考学习discuss中swap元素的思想

<109>.（719:Hard）(非常经典题)Find K-th Smallest Pair Distance

• 该题非常巧妙的使用了二分查找的思想。对于输入数组nums，我们首先对nums数组进行排序，然后寻找两两相隔的数字中有最小差的pair，将其定为二分查找的low值，然后取nums[-1]-nums[0]作为二分查找的high值（因为最大数和最小数的差一定最大），那么mid=low+(high-mid)//2，接下来的任务就是二分查找第k个最小值。这里需要注意：1、 可能nums数组中不存在一对pair满足两数差的值“恰好”为low+(high-mid)//2，但我们在接下来的二分查找中，可以根据“小于等于mid值的pairs个数”，保证最终返回的值是存在的一对pair的差值 2、此处的low、high代表的是两数的差值，而不是下标索引。
• 承接上面的思路，我们编写一个countPairs的函数来求得当前nums数组中。pairs差值小于等于mid值的个数小于mid值时，low=mid+1，否则high=mid。这个countPairs函数不能以最简单的遍历形式来运行，因为会超时，即下面的countPairs代码是time limit的。

  def countPairs(self, nums, mid):        #计算差值小于等于mid的pair个数
      n = len(nums)
      numbers = 0
      for i in range(n):
          j = i
          while(j < n and nums[j] - nums[i] <= mid):
              j += 1          #j就是第一个刚好比nums[i]+mid大的第一个数的索引
          numbers += j - i - 1
      return numbers

• 因此，我们采用二分查找的方式寻找上面函数中j的值，下面函数中i、j、low、high、mid均是下标索引。

  def countPairs(self, nums, mid):        #计算差值小于等于mid的pair个数
      n = len(nums)
      numbers = 0
      for i in range(n):
          """
          j = i
          while(j < n and nums[j] - nums[i] <= mid):
              j += 1          #j就是第一个刚好比nums[i]+mid大的第一个数的索引
          numbers += j - i - 1
          """
          numbers += self.upperBound(nums, i, n - 1, nums[i] + mid) - i - 1 #upperBound函数返回的其实就是上面的j值
      return numbers

  def upperBound(self, nums, low, high, key):  #high = len(nums) - 1   key=nums[low] + mid
      if(nums[high] <= key):
          return high + 1
      while(low < high):
          mid = low + (high - low) // 2
          if(nums[mid] <= key):
              low = mid + 1
          else:
              high = mid
      return low

上面的方法只beat 22%，且只用到了binary search而没有其他的技巧，discuss中还有结合heap的更快的思路，下次复习时应仔细研究学习

<110>.（4:Hard）（非常经典题）Median of Two Sorted Arrays

• 该题其实可以看做两个已排序数组待merge的过程，当我们已经merge的数组长度成为了两个数组总长度的二分之一时，说明已经找到了median，只不过时间复杂度为O(n)，不符合题意。下边我将dicuss中的最高票解释誊写在这里，并加上我自己的一些理解。
• To solve this problem, we need to understand “What is the use of median”. In statistics, the median is used for dividing a set into two equal length subsets, that one subset is always greater than the other. If we understand the use of median for dividing, we are very close to the answer.
• First let’s cut A into two parts at a random position i:

        left_A             |        right_A
  A[0], A[1], ..., A[i-1]  |  A[i], A[i+1], ..., A[m-1]

• Since A has m elements, so there are m+1 kinds of cutting( i = 0 ~ m ). And we know: len(left_A) = i, len(right_A) = m - i . Note: when i = 0 , left_A is empty, and when i = m , right_A is empty.
• With the same way, cut B into two parts at a random position j:

        left_B             |        right_B
  B[0], B[1], ..., B[j-1]  |  B[j], B[j+1], ..., B[n-1]

• Put left_A and left_B into one set, and put right_A and right_B into another set. Let’s name them left_part and right_part :

        left_A             |        right_A
  A[0], A[1], ..., A[i-1]  |  A[i], A[i+1], ..., A[m-1]
  B[0], B[1], ..., B[j-1]  |  B[j], B[j+1], ..., B[n-1]

• If we can ensure:

  1) len(left_part) == len(right_part)
  2) max(left_part) <= min(right_part)

• then we divide all elements in {A, B} into two parts with equal length, and one part is always greater than the other. Then median = (max(left_part) + min(right_part))/2.
• To ensure these two conditions, we just need to ensure:

  (1) i + j == m - i + n - j (or: m - i + n - j + 1)（m-i是数组A右部分的长度，n-j是数组B右部分的长度）
      if n >= m, we just need to set: i = 0 ~ m, j = (m + n + 1)/2 - i（也就是j + i = (m + n + 1)/2）
  (2) B[j-1] <= A[i] and A[i-1] <= B[j]

• ps.1 For simplicity, I presume A[i-1],B[j-1],A[i],B[j] are always valid even if i=0/i=m/j=0/j=n（在寻找i时，判断条件中会用到A[i-1],B[j-1],A[i],B[j]，所以在i、j取边界值的时候我们需要特殊注意） . I will talk about how to deal with these edge values at last.
• ps.2 Why n >= m? Because I have to make sure j is non-nagative since 0 <= i <= m and j = (m + n + 1)/2 - i. If n < m , then j may be nagative, that will lead to wrong result.
• So, all we need to do is:

  Searching i in [0, m], to find an object `i` that:
      B[j-1] <= A[i] and A[i-1] <= B[j], ( where j = (m + n + 1)/2 - i )

• And we can do a binary search following steps described below:

  <1> Set imin = 0, imax = m, then start searching in [imin, imax]
  
  <2> Set i = (imin + imax)/2, j = (m + n + 1)/2 - i
  
  <3> Now we have len(left_part)==len(right_part). And there are only 3 situations
       that we may encounter:
      <a> B[j-1] <= A[i] and A[i-1] <= B[j]
          Means we have found the object `i`, so stop searching.
      <b> B[j-1] > A[i]
          Means A[i] is too small. We must `ajust` i to get `B[j-1] <= A[i]`.
          Can we `increase` i?
              Yes. Because when i is increased, j will be decreased.
              So B[j-1] is decreased and A[i] is increased, and `B[j-1] <= A[i]` may
              be satisfied.
          Can we `decrease` i?
              `No!` Because when i is decreased, j will be increased.
              So B[j-1] is increased and A[i] is decreased, and B[j-1] <= A[i] will
              be never satisfied.
          So we must `increase` i. That is, we must ajust the searching range to
          [i+1, imax]. So, set imin = i+1, and goto <2>.
      <c> A[i-1] > B[j]
          Means A[i-1] is too big. And we must `decrease` i to get `A[i-1]<=B[j]`.
          That is, we must ajust the searching range to [imin, i-1].
          So, set imax = i-1, and goto <2>.

• When the object i is found, the median is:

  max(A[i-1], B[j-1]) (when m + n is odd)
  or (max(A[i-1], B[j-1]) + min(A[i], B[j]))/2 (when m + n is even)

• Now let’s consider the edges values i=0,i=m,j=0,j=n where A[i-1],B[j-1],A[i],B[j] may not exist. Actually this situation is easier than you think.
• What we need to do is ensuring that max(left_part) <= min(right_part). So, if i and j are not edges values(means A[i-1],B[j-1],A[i],B[j] all exist), then we must check both B[j-1] <= A[i] and A[i-1] <= B[j]. But if some of A[i-1],B[j-1],A[i],B[j] don’t exist, then we don’t need to check one(or both) of these two conditions. For example, if i=0, then A[i-1] doesn’t exist, then we don’t need to check A[i-1] <= B[j]. So, what we need to do is:

  Searching i in [0, m], to find an object `i` that:
      (j == 0 or i == m or B[j-1] <= A[i]) and
      (i == 0 or j == n or A[i-1] <= B[j])
      where j = (m + n + 1)/2 - i

• And in a searching loop, we will encounter only three situations:

  <a> (j == 0 or i == m or B[j-1] <= A[i]) and
      (i == 0 or j = n or A[i-1] <= B[j])
      Means i is perfect, we can stop searching.
  
  <b> j > 0 and i < m and B[j - 1] > A[i]
      Means i is too small, we must increase it.
  
  <c> i > 0 and j < n and A[i - 1] > B[j]
      Means i is too big, we must decrease it.

• Actually, here i < m ==> j > 0 and i > 0 ==> j < n

  m <= n, i < m ==> j = (m+n+1)/2 - i > (m+n+1)/2 - m >= (2*m+1)/2 - m >= 0    
  m <= n, i > 0 ==> j = (m+n+1)/2 - i < (m+n+1)/2 <= (2*n+1)/2 <= n

• So in situation 《b》 and 《c》, we don’t need to check whether j > 0 and whether j < n.

参考链接：[Discuss中二分查找思路](https://leetcode.com/problems/median-of-two-sorted-arrays/discuss/2481/Share-my-O(log(min(mn))-solution-with-explanation)

上面的方法beat 46%，时间复杂度应为O(log(min(m,n)))，下次复习时应参考是否还有其他更快的解法

上面的解释太冗余，请参看下面的解法思路：

• 该方法的核心是将原问题转变成一个寻找第k小数的问题（假设两个原序列升序排列），这样中位数实际上是第(m+n)/2小的数。所以只要解决了第k小数的问题，原问题也得以解决。
• 首先假设数组A和B的元素个数都大于k/2，我们比较A[k/2-1]和B[k/2-1]两个元素，这两个元素分别表示A的第k/2小的元素和B的第k/2小的元素。这两个元素比较共有三种情况：>、<和=。如果A[k/2-1]<B[k/2-1]，这表示A[0]到A[k/2-1]的元素都在A和B合并之后的前k小的元素中。换句话说，A[k/2-1]不可能大于两数组合并之后的第k小值，所以我们可以将其抛弃。

证明也很简单，可以采用反证法。

1. 假设A[k/2-1]大于合并之后的第k小值，我们不妨假定其为第（k+1）小值。由于A[k/2-1]小于B[k/2-1]，所以B[k/2-1]至少是第（k+2）小值。但实际上，在A中至多存在k/2-1个元素小于A[k/2-1]，B中也至多存在k/2-1个元素小于A[k/2-1]，所以小于A[k/2-1]的元素个数至多有k/2+ k/2-2，小于k，这与A[k/2-1]是第（k+1）的数矛盾。
2. 当A[k/2-1]>B[k/2-1]时存在类似的结论。
3. 当A[k/2-1]=B[k/2-1]时，我们已经找到了第k小的数，也即这个相等的元素，我们将其记为m。由于在A和B中分别有k/2-1个元素小于m，所以m即是第k小的数。(这里可能有人会有疑问，如果k为奇数，则m不是中位数。这里是进行了理想化考虑，在实际代码中略有不同，是先求k/2，然后利用k-k/2获得另一个数。)

• 通过上面的分析，我们即可以采用递归的方式实现寻找第k小的数。此外我们还需要考虑几个边界条件：

1. 如果A或者B为空，则直接返回B[k-1]或者A[k-1]；
2. 如果k为1，我们只需要返回A[0]和B[0]中的较小值；
3. 如果A[k/2-1]=B[k/2-1]，返回其中一个；

• 参考链接：想搞懂该题必看的教程1 想搞懂该题必看的教程2

<111>.（126:Hard）（非常非常难）Word Ladder II

• 参考链接：分析1 分析2

该题非常难，涉及图算法BFS、DFS，因未复习至此，所以并未做详细考虑，下次复习时需要仔细研究该题

112.（896:Easy）Monotonic Array

• 直接看代码

    public boolean isMonotonic(int[] A) {
        if (A.length==1) return true;
        int n=A.length;
        boolean up= (A[n-1]-A[0])>0;
        for (int i=0; i<n-1; i++)
            if (A[i+1]!=A[i] && (A[i+1]-A[i]>0)!=up)    //检查相邻元素和首尾元素是否是相同的增减性
                return false;
        return true;
    }

113.（498:Easy）Diagonal Traverse

• Walk patterns:

1. If out of bottom border (row >= m) then row = m - 1; col += 2; change walk direction.
2. if out of right border (col >= n) then col = n - 1; row += 2; change walk direction.
3. if out of top border (row < 0) then row = 0; change walk direction.
4. if out of left border (col < 0) then col = 0; change walk direction.
5. Otherwise, just go along with the current direction.

Time complexity: O(m * n), m = number of rows, n = number of columns.

Space complexity: O(1).

• 注意：row>=m和col>=n的优先级要比row<0和col<0的优先级高，且row和col超出上界时，行和列坐标都要更新。代码如下：

    public int[] findDiagonalOrder(int[][] matrix) {
        if (matrix == null || matrix.length == 0) return new int[0];
        int m = matrix.length, n = matrix[0].length;
        
        int[] result = new int[m * n];
        int row = 0, col = 0, d = 0;
        int[][] dirs = {{-1, 1}, {1, -1}}; //方向移动数组，斜向移动
        
        for (int i = 0; i < m * n; i++) {
            result[i] = matrix[row][col];
            row += dirs[d][0];
            col += dirs[d][1];
            
            //注意row>=m和col>=n的优先级要比row<0和col<0的优先级高
            //row和col超出上界时，行和列坐标都要更新
            if (row >= m) { row = m - 1; col += 2; d = 1 - d;}  
            if (col >= n) { col = n - 1; row += 2; d = 1 - d;}
            if (row < 0)  { row = 0; d = 1 - d;}
            if (col < 0)  { col = 0; d = 1 - d;}
        }
        
        return result;
    }

114.（413:Medium）（非常非常经典题）Arithmetic Slices

• 请参看如下代码，O(n)时间复杂度

public int numberOfArithmeticSlices(int[] A) {
    int curr = 0, sum = 0;  //sum是结果集，curr是以当前数字为尾的符合条件的slice数量
    for (int i=2; i<A.length; i++)
        if (A[i]-A[i-1] == A[i-1]-A[i-2]) {
            //if A[i-2], A[i-1], A[i] are arithmetic, then the number of arithmetic slices ending with A[i] (dp[i])
            // equals to:
            //      the number of arithmetic slices ending with A[i-1] (dp[i-1], all these arithmetic slices appending A[i] are also arithmetic)
            //      +
            //      A[i-2], A[i-1], A[i] (a brand new arithmetic slice)
            // it is how dp[i] = dp[i-1] + 1 comes
            curr += 1; 
            sum += curr;
        } else {
            curr = 0;
        }
    return sum;
}

• DP思路：

    int numberOfArithmeticSlices(vector<int>& A) {
        int n = A.size();
        if (n < 3) return 0;
        vector<int> dp(n, 0); // dp[i] means the number of arithmetic slices ending with A[i]
        if (A[2]-A[1] == A[1]-A[0]) dp[2] = 1; // if the first three numbers are arithmetic or not
        int result = dp[2];
        for (int i = 3; i < n; ++i) {
            // if A[i-2], A[i-1], A[i] are arithmetic, then the number of arithmetic slices ending with A[i] (dp[i])
            // equals to:
            //      the number of arithmetic slices ending with A[i-1] (dp[i-1], all these arithmetic slices appending A[i] are also arithmetic)
            //      +
            //      A[i-2], A[i-1], A[i] (a brand new arithmetic slice)
            // it is how dp[i] = dp[i-1] + 1 comes
            if (A[i]-A[i-1] == A[i-1]-A[i-2]) 
                dp[i] = dp[i-1] + 1;
            result += dp[i]; // accumulate all valid slices
        }
        return result;
    }

115.（849:Easy）Maximize Distance to Closest Person

• 只需要记录数组元素为1的下标即可，比较相邻两1值所在的位置，即可得到最大的距离。需要特殊处理第一个1元素，参考代码如下：

public int maxDistToClosest(int[] seats) {
    int i, j, res = 0, n = seats.length;
    for (i = j = 0; j < n; ++j) //i记录了上一个1值的下一个位置，j记录新的1值位置
        if (seats[j] == 1) {
            if (i == 0) res = Math.max(res, j - i); 
            else res = Math.max(res, (j - i + 1) / 2);
            i = j + 1;
        }
    res = Math.max(res, n - i);
    return res;
}

116.（457:Medium）（经典题）Circular Array Loop

• 这道题描述的并不是很清楚，比如题目中有句话说循环必须是forward或是backward的，如果不给例子说明，不太容易能get到point。所谓的循环必须是一个方向的就是说不能跳到一个数，再反方向跳回来，这不算一个loop。比如[1, -1]就不是一个loop，而[1, 1]是一个正确的loop。弄清楚了题意后来考虑如何做，由于从一个位置只能跳到一个别的位置，而不是像图那样一个点可以到多个位置，所以这里我们就可以根据坐标建立一对一的映射，一旦某个达到的坐标已经有映射了，说明环存在，当然我们还需要进行一系列条件判断。
• 首先我们需要一个visited数组，来记录访问过的数字，然后我们遍历原数组，如果当前数字已经访问过了，直接跳过，否则就以当前位置坐标为起始点开始查找，进行while循环，将当前位置在visited数组中标记true，然后计算下一个位置，计算方法是当前位置坐标加上对应的数字，由于是循环数组，所以结果可能会超出数组的长度，所以我们要对数组长度取余。当然上面的数字也可能是负数，加完以后可能也是负数，所以光取余还不够，还得再补上一个n，使其变为正数。此时我们判断，如果next和cur相等，说明此时是一个数字的循环，不符合题意，再有就是检查二者的方向，数字是正数表示forward，若是负数表示backward，在一个loop中必须同正或同负，我们只要让二者相乘，如果结果是负数的话，说明方向不同，直接break掉。此时如果next已经有映射了，说明我们找到了合法的loop，返回true，否则建立一个这样的映射，继续循环。

117.（905:Easy）Sort Array By Parity

• 该题设立两个指针i和j，分别指向array数组的开头和结尾。当前的数字是偶数时，存在i指针指向的位置；当前的数字是奇数时，存在j指针指向的位置。

118.（825:Medium）Friends Of Appropriate Ages

    public int numFriendRequests(int[] ages) {
        int count = 0, count_ages[] = new int[121], count_no_more_than_ages[] = new int[121];  //最大年龄为121，count是结果变量    
        for(int age: ages) count_ages[age]++;   //统计不同年龄的人数
        for(int ageA = 15; ageA<=120; ageA++){ //only older can sent request to younger or peer，注意age从15开始，是因为要同时满足两个条件不为真：age[B] <= 0.5 * age[A] + 7，age[B] > age[A]。否则不会发送request    
            count_no_more_than_ages[ageA]=count_ages[ageA]+count_no_more_than_ages[ageA-1]; //统计比当前年龄小或同龄的人的个数
            if(count_ages[ageA]==0) continue;  //当前年龄没人就跳过，因为该年龄不可能发request
            //count_no_more_than_ages[ageA]-count_no_more_than_ages[ageA/2+7] is the number of younger or peer <= ageA
            //-1 means people can't sent request to himself
            count+=count_ages[ageA]*(count_no_more_than_ages[ageA]-count_no_more_than_ages[ageA/2+7]-1); //减去count_no_more_than_ages[ageA/2+7]是因为保证该条件不为true，age[B] <= 0.5 * age[A] + 7
        }
        return count;
    }

119.（548:Medium）（非常非常经典题）Split Array with Equal Sum

• 这种将数组多分割的问题，首先都需要先固定中间指针的位置即确定中间指针的活动范围，然后再移动首尾指针。

    public boolean splitArray(int[] nums) {
        if (nums.length < 7)
            return false;
        int[] sum = new int[nums.length]; //累加和数组
        sum[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            sum[i] = sum[i - 1] + nums[i];
        }
        for (int j = 3; j < nums.length - 3; j++) { //确定中间指针的活动范围,这种将数组多分割的问题，首先都需要先固定中间指针的位置，然后再移动首尾指针
            HashSet<Integer> set = new HashSet<>(); 
            for (int i = 1; i < j - 1; i++) {
                if (sum[i - 1] == sum[j - 1] - sum[i])  //先确定前半部分的符合值，按定义来求值即可
                    set.add(sum[i - 1]);
            }
            for (int k = j + 2; k < nums.length - 1; k++) { //再遍历后半部分的符合值，且该值要与前半部分相同，按定义来求值即可
                if (sum[nums.length - 1] - sum[k] == sum[k - 1] - sum[j] && set.contains(sum[k - 1] - sum[j]))
                    return true;
            }
        }
        return false;
    }

120.（419:Medium）（非常经典题）Battleships in a Board

• 高效的方法：Going over all cells, we can count only those that are the "first" cell of the battleship. First cell will be defined as the most top-left cell. We can check for first cells by only counting cells that do not have an 'X' to the left and do not have an 'X' above them.

    public int countBattleships(char[][] board) {
        int m = board.length;
        if (m==0) return 0;
        int n = board[0].length;
        
        int count=0;
        
        for (int i=0; i<m; i++) {
            for (int j=0; j<n; j++) {
                if (board[i][j] == '.') continue;
                if (i > 0 && board[i-1][j] == 'X') continue;
                if (j > 0 && board[i][j-1] == 'X') continue;
                count++;
            }
        }
        
        return count;
    }

121.（977:Easy）（非常经典题）Squares of a Sorted Array

• 该题利用了双指针的思想，是利用了该输入数组的特性，因为较大的squared numbers的值只能从输入数组的最开始(负数)或最末尾(正数)中取，所以从后往前的填充result数组

    public int[] sortedSquares(int[] A) {
        int n = A.length;
        int[] result = new int[n];
        int i = 0, j = n - 1;
        for (int p = n - 1; p >= 0; p--) {
            if (Math.abs(A[i]) > Math.abs(A[j])) {
                result[p] = A[i] * A[i];
                i++;
            } else {
                result[p] = A[j] * A[j];
                j--;
            }
        }
        return result;
    }

122.（540:Medium）（非常非常经典题）Single Element in a Sorted Array

• 感觉是一道比较tricky的题目，需要观察题目例子的特征，才能给出符合要求的答案。正如题目的限制条件所说，如果需要在O(logn)时间复杂度下解决这个问题，一定是要用到二分查找。
• 因为题目中给的条件是sorted array，我们观察例子 [1,1,2,3,3,4,4,8,8]，假如当索引i左侧没有只出现一次的数字，那么所有左侧的数字都是两两配对的，也就是说2j和2j+1两个数字一定是相等的。但是，若当索引i是偶数时，它和i+1位置的数字不相等；或者，当索引i是奇数时，它和i-1位置的数字不相等，那么这两种情况就说明，在索引i及其左侧一定是有一个只出现一次的落单数字。
• 此外，我们还能发现，落单的数字一定是在偶数索引位置上。
• 基于以上分析，我们可以写出binary search的解法，具体可以参考代码实现。参考视频：花花讲解视频

123.（334:Medium）（非常经典题）Increasing Triplet Subsequence

• The main idea is keep two values when check all elements in the array: the minimum value min until now and the second minimum value secondMin from the minimum value's position until now. Then if we can find the third one that larger than those two values at the same time, it must exists the triplet subsequence and return true.
• What need to be careful is: we need to include the condition that some value has the same value with minimum number（当当前位置的数字与之前最小的数字相同时，并不更新次小的数字，相当于将之前的次小数看作无效，因为我们要的是递增的子序列，需要考虑次序关系）, otherwise this condition will cause the secondMin change its value.
• 参考代码如下：

public boolean increasingTriplet(int[] nums) {
    int min = Integer.MAX_VALUE, secondMin = Integer.MAX_VALUE; //当当前的数同时大于最小的数和次小的数时，返回true
    for(int num : nums){
        if(num <= min) min = num; //当当前的数比最小的数还小时(或等于)，次小的数不更新相当于无效，因为考虑到了次序关系
        else if(num < secondMin) secondMin = num;
        else if(num > secondMin) return true;
    }
    return false;
}

124.（912:Medium）（经典题）Sort an Array

• 考察的就是排序算法，需要温习

125.（1002:Medium）Find Common Characters

• 计算每个单词里各个字符的出现频率,取所有单词的字符出现频率的最小值。

126.（821:Easy）(非常非常经典题)Shortest Distance to a Character

• Two pass: First forward pass to find shortest distant to character on left. Second backward pass to find shortest distant to character on right.

127.（941:Easy）(经典题)Valid Mountain Array

• Two pointers climb from left and from right separately. If they are climbing the same mountain, they will meet at the same point.

128.（840:Easy）（Google面经题）Magic Squares In Grid

• The center of the square must be 5.
• Besides, I judge whether 1. the square contains number 1~9. 2. the four sides and two diagonal lines all equal to 15.
• 为什么中心数是5?每行或每列的和为15?原因：https://blog.csdn.net/firefly_2002/article/details/7886989

129.（723:Medium）（非常经典题）Candy Crush

• The idea is to traverse the entire matrix again and again to remove crush until no crush can be found.
• For each traversal of the matrix, we only check two directions: rightward and downward. There is no need to check upward and leftward because they would have been checked from previous cells.
• For each cell, if there are at least three candies of the same type rightward or downward, set them all to its negative value to mark them.
• After each traversal, we need to remove all those negative values by setting them to 0, then let the rest drop down to their correct position. A easy way is to iterate through each column, for each column, move positive values to the bottom then set the rest to 0.

130.（969:Medium）（经典题）Pancake Sorting

• 思路是:每次循环都将当前最大的元素放到他应当在的位置上。我们从最大的数字n开始找起，先找到当前最大的元素位置索引，将其放到A[0]上，再将它从A[0]放到它应该在的位置上，然后开始找次大的元素。思路如下：

// 思路是，每次循环都将当前最大的元素放到他应当在的位置上
public List<Integer> pancakeSort(int[] A) {
    List<Integer> result = new ArrayList<>();
    int n = A.length, largest = n; // 从最大的数字n开始放置
    for (int i = 0; i < n; i++) {
        int index = find(A, largest); //找到最大的元素位置
        flip(A, index); //先将其放到A[0]上
        flip(A, largest - 1); //再将它从A[0]放到它应该在的位置上
        result.add(index + 1);
        result.add(largest--);
    }
    return result;
}
    
private int find(int[] A, int target) {
    for (int i = 0; i < A.length; i++) {
        if (A[i] == target) {
            return i;
        }
    }
    return -1;
}
    
private void flip(int[] A, int index) {
    int i = 0, j = index;
    while (i < j) {
        int temp = A[i];
        A[i++] = A[j];
        A[j--] = temp;
    }
}

131.（900:Medium）（非常非常经典题）RLE Iterator

• 该题有两个诀窍：1.计算剩余需要访问的元素个数 2.比较当前访问的索引是否超出最大的长度。

    int index;
    int [] A;
    public _900_RLEIterator(int[] A) {
        this.A = A;
        index = 0; //用来定位当前访问的A数组的元素位置
    }

    public int next(int n) {
        while(index < A.length && n > A[index]){
            n = n - A[index]; //更新剩余需要访问的元素个数
            index += 2; //每次index加2，访问下一个元素的个数
        }

        if(index >= A.length){
            return -1;
        }

        A[index] = A[index] - n; //更新当前元素的剩余个数
        return A[index + 1]; //index指向的是当前元素的个数，index+1指向的是当前的元素
    }

132.（1007:Medium）（非常经典题）Minimum Domino Rotations For Equal Row

• 该题intuitive会想到，符合条件的数组在交换后，要么一个数组的元素全部是A[0]，要么一个数组的元素全部是B[0]，所以我们要么将A、B数组全部变成A[0]，要么将A、B数组全部变成B[0]。

public int minDominoRotations(int[] A, int[] B) {
    int n = A.length;
    //以A[0]为基准，将A数组或B数组的元素都变成A[0]，用a来记录将数组A全部变成A[0]需要交换的次数，用b来记录将数组B全部变成A[0]需要交换的次数
    for (int i = 0, a = 0, b = 0; i < n && (A[i] == A[0] || B[i] == A[0]); ++i) {
        if (A[i] != A[0]) a++;
        if (B[i] != A[0]) b++;
        if (i == n - 1) return Math.min(a, b);
    }
    //以B[0]为基准，将A数组或B数组的元素都变成B[0]，用a来记录将数组A全部变成B[0]需要交换的次数，用b来记录将数组B全部变成B[0]需要交换的次数
    for (int i = 0, a = 0, b = 0; i < n && (A[i] == B[0] || B[i] == B[0]); ++i) {
        if (A[i] != B[0]) a++;
        if (B[i] != B[0]) b++;
        if (i == n - 1) return Math.min(a, b);
    }
    return -1;
}

• 教学视频：视频讲解

133.（126:Hard）（非常经典题）Word Ladder II

• 核心思路：首先通过BFS确认存在一条从start到end的路径，并且建立从start到各个有效字符串的距离及各个有效字符串的valid neighbors，之后利用DFS找到所有的路径并返回
• The basic idea is:

1. Use BFS to find the shortest distance between start and end, tracing the distance of crossing nodes from start node to end node, and store node's next level neighbors to HashMap;

2. Use DFS to output paths with the same distance as the shortest distance from distance HashMap: compare if the distance of the next level node equals the distance of the current node + 1.

134.（1146:Medium）（非常经典题）Snapshot Array

• The idea is, the whole array can be large, and we may take the snap tons of times. (Like you may always ctrl + S twice)
• Instead of record the history of the whole array, we will record the history of each cell. And this is the minimum space that we need to record all information.
• For each A[i], we will record its history with a snap_id and a its value. When we want to get the value in history, just binary search the time point.

TreeMap<Integer, Integer>[] A; //A[i]存储的是数组第i个索引元素的版本号和对应版本号的值
int snap_id = 0;
public _1146_SnapshotArray(int length) {
    A = new TreeMap[length];
    for (int i = 0; i < length; i++) {
        A[i] = new TreeMap<Integer, Integer>();
        A[i].put(0, 0); //初始化
    }
}

public void set(int index, int val) {
    A[index].put(snap_id, val);
}

public int snap() {
    return snap_id++;
}

public int get(int index, int snap_id) {
    return A[index].floorEntry(snap_id).getValue();
}