Modul 4 - Schematics-NPC-2021/Tutorial-Schematics-NPC-Junior-2021 GitHub Wiki
Graf adalah sekumpulan vertex/node yang dihubungkan oleh nol atau lebih edge.
-
weight- "berat" dari suatu edge. dapat juga diartikan sebagai panjang sebuah edge. -
un/weighted graph- istilah dimana edge pada suatu graf memiliki/tidak memiliki weight. -
un/directed edge- istilah untuk menyatakan apabila sebuah edge bersifat dua arah/satu arah. -
path- urutan satu atau lebih edge yang dilewati untuk menghubungkan dua buah vertex. -
connected- sebuah graf dimana terdapat setidaknya satu buah path untuk setiap pasang vertex. -
cycle- sebuah path yang berawal dan berakhir pada satu buah vertex yang sama tanpa melewati dua buah edge yang sama. -
tree- sebuah undirected connected graf yang tidak memiliki cycle. -
root- vertex dengan kedalaman ter-rendah. -
ancestor- himpunan vertex yang dilewati dalam suatu path dari root ke sebuah vertex. -
parent- ancestor suatu node yang memiliki kedalaman tertinggi. -
child- kumpulan vertex yang terhubung dengan suatu edge dan bukan merupakan ancestor.
Terdapat 3 cara yang sering dipakai untuk merepresentasikan sebuah graf, yaitu
- Adjacency Matrix
Kita bisa merepresentasikan graf dengan menggunakan array 2 dimensiAdjmat[V][V]dengan AdjMat[i][j] bernilai 1 apabila terdapat edge yang menghubungkan vertex i dan vertex j dan 0 jika tidak ada. Nilai AdjMat[i][j] bisa juga bernilai weight dari suatu edge untuk weighted graf.
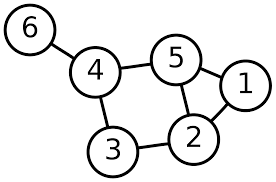
Sebagai contoh, adjacency matrix untuk graf pada contoh adalah sebagai berikut:
0 1 0 0 1 0
1 0 1 0 1 0
0 1 0 1 0 0
0 0 1 0 1 1
1 1 0 1 0 0
0 0 0 1 0 0- Adjacency List
Masalah utama dari penggunaan adjacency matrix adalah penggunaan memory yang menghabiskan sebanyak$V^2$ memory untuk graf dengan banyak vertex sebanyak$V$ sehingga tidak memungkinkan untuk graf dengan ukuran besar.
Solusi permasalahan tersebut adalah dengan menggunakan Adjacency List. Ide dari perepresentasian dengan menggunakan Adjacency List adalah dengan hanya menyimpan daftar dari vertex-vertex lain yang memiliki edge yang terhubung dengan suatu vertex. Pengimplementasiannya dapat dilakukan dengan menggunakan vector seperti berikut:
vector< int > adjList[V];
//memasukkan edge a-b
adjList[a].push_back(b);
adjList[b].push_back(a);untuk weighted graf kita dapat menggunakan pair<int,int> sebagai isi dari Adjacency List untuk menyimpan vertex yang adjacent beserta weightnya.
Berikut implementasi untuk weighted graf :
vector< pair<int,int> > adjList[V];
//memasukkan edge a-b dengan weight c
adjList[a].push_back(make_pair(b,c));
adjList[b].push_back(make_pair(a,c));penggunaan metode ini dalam merepresentasikan graf sangat direkomendasikan karena sangat efisien dalam penggunaan memori maupun kompleksitas waktu dalam melakukan traversal.
- Edge List
Ide dari perepresentasian graf dengan metode ini adalah dengan menyimpan semua daftar edge yang ada dalam suatu graf. Penyimpanan dapat dilakukan di dalam sebuah array statis maupun dinamis sepertivector
Pengimplementasiannya dapat menggunakan struct yang berisi vertex yang berada diujung edge tersebut beserta weight nya. Alternatif lain jika mager membuat struct adalah menggunakan sebuahpair<pair<int,int>,int>untuk menyimpan informasi yang dibutuhkan tadi.
Contoh implementasinya adalah sebagai berikut:
vector< pair<pair<int,int>,int> > edgeList;
// memasukkan edge a-b dengan weight c
edgeList.push_back(make_pair(make_pair(a,b),c));Untuk unweighted graf kita dapat mengganti isi dari vector menjadi pair<int,int>.
Metode ini sangat berguna dalam algoritma kruskal untuk mencari Minimum Spanning Tree dari sebuah graf
Note : meskipun terlihat sedikit lebih ribet, penulis lebih menyukai opsi menggunakan pair karena sesungguhnya pakai struct lebih malesin. ehe.
Dalam beberapa kasus, kita tidak memerlukan suatu struktur data khusus untuk menyimpan suatu graf agar bisa ditelusuru ataupun dioperasikan. Kasus-kasus tersebut terjadi jika graf berbentuk implicit graph.
2 Bentuk umum dari implicit graph yaitu :
- Graf dengan edge yang implisit
Contoh 1:
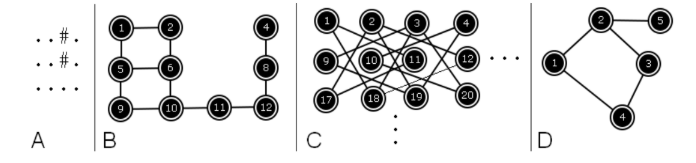
Seperti yang kalian sering jumpai pada modul rekursi di dasar pemrograman, yaitu sebuah grid yang berisi karakter '.' ataupun '#' dimana kita tidak bisa mengunjungi grid yang berisi '#'. (Gambar A)
Secara tidak sadar, ini adalah sebuah graf dengan vertexnya merupakan posisi yang berisi '.' serta edgenya menghubungkan dua buah '.' yang saling bersentuhan. (Gambar B)
Dapat dilihat bahwa kita tidak memerlukan salah satu dari 3 teknik merepresentasikan graf seperti yang dijelaskan sebelumnya.
Contoh 2:
Graf yang dibentuk berdasarkan pergerakan bidak kuda pada permainan catur. Kita dapat menganggap petak-petak pada catur sebagai vertex dari graf, serta sebuah edge menghubungkan 2 buah petak jika petak tersebut dapat dikunjungi dengan melakukan langkah bidak kuda. (Gambar C) - Graf dengan edge yang mengikuti suatu peraturan
Contoh:
Graf dengan N vertex ([1..N]) dimana terdapat edge yang menghubungkan$i$ dan$j$ jika$(i+j)$ adalah prima. (Gambar D)
Sesuai dengan namanya, DFS akan melakukan traversal sampai ke vertex yang paling 'dalam'. Setiap kali sampai di suatu vertex
Contoh pengimplementasian dalam weighted graf dapat dilakukan secara rekursif seperti kode berikut:
vector<pair<int,int>> adjList[N];
bool visited[N];
void dfs(int curVertex)
{
//menandai bahwa vertex ini sudah pernah dikunjungi
visited[curVertex] = 1; //Perhatikan baris ini untuk trivia question
for (int i = 0 ; i < adjList[curVertex].size() ; i++) //menelusuri daftar vertex yang terhubung dengan curVertex
{
int nextVertex = adjList[curVertex][i].first;
//perhatikan bahwa dalam pair,
// first merupakan nomor vertex serta second
//merupakan weightnya
if (!visited[nextVertex]) //mengecek jika belum dikunjungi
{
dfs(adjList[curVert]);
//do something
}
}
//do something
}Traversal menggunakan BFS dimulai dari sebuah vertex, lalu akan mengunjungi vertex yang terhubung langsung dengan vertex tersebut (layer 1). Lalu, di langkah selanjutnya akan mengunjungi vertex yang terhubung langsung dengan vertex - vertex pada layer 1 (layer 2) dan seterusnya sampai sudah tidak ada lagi vertex yang bisa dikunjungi.
Berbeda dengan DFS, pengimplementasian BFS dapat dilakukan secara iteratif dengan menggunakan bantuan queue seperti berikut :
vector<int> adjList[N];
bool visited[N];
void bfs(int startNode)
{
queue<int> q;
q.push(startNode);
visited[startNode] = 1;
while (!q.empty()) // ada yang tau kenapa seperti ini?
{
int curNode = q.front();
q.pop();
for (int i = 0 ; i < adj[curNode].size() ; i++) // sama seperti DFS
{
int nextNode = adj[curNode][i];
if (!visited[nextNode])
{
q.push(nextNode);
vis[nextNode] = 1; //Perhatikan baris ini untuk trivia question
}
}
}
}Trivia question : pada DFS, kita melakukan penandaan pada node sebelum mengiterasi isi dari adjacency list, sedangkan pada BFS, kita melakukan penandaan di dalam iterasi. Apakah timing penempatan tanda ini berpengaruh pada algoritma-algoritma tersebut? Jika iya, apa pengaruhnya?

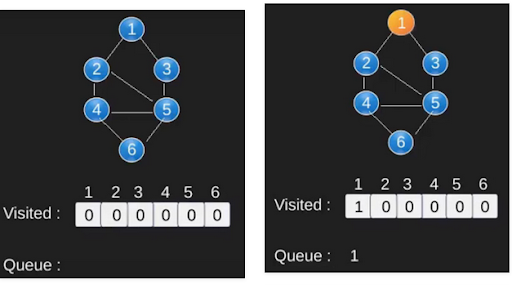
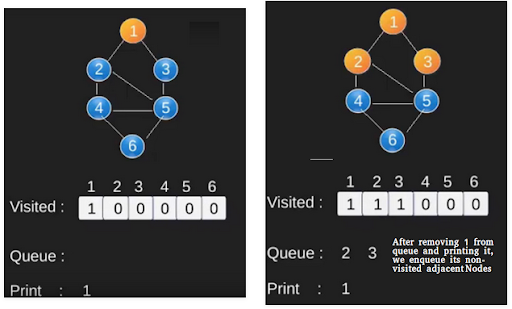
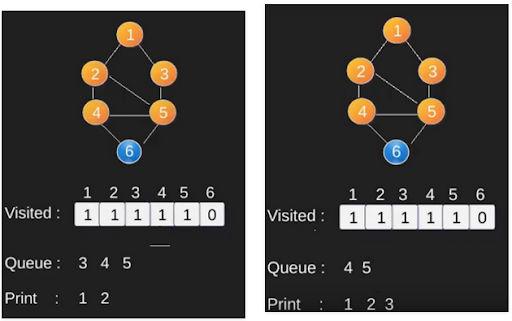
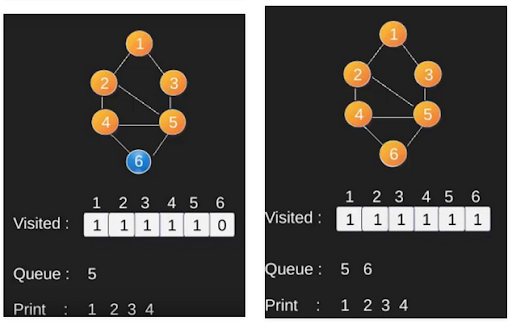
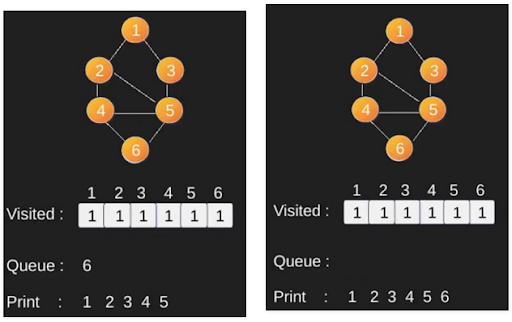
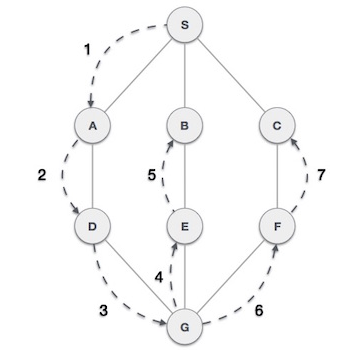
Jika kita melakukan BFS pada graf tersebut dari vertex 1, maka vertex-vertex tiap layer adalah:
- Layer 0 : 1
- Layer 1 : 2 5
- Layer 2 : 3 4
- Layer 3 : 6
Perhatikan bahwa jumlah layer adalah jumlah dari edge minimal yang harus dilewati untuk sampai ke vertex tersebut dari vertex 1 atau biasa disebut dengan shortest path.
BFS adalah algoritma traversing di mana Anda harus mulai traverse dari node yang dipilih (sumber atau node mulai) dan melintasi graph secara melebar hingga menjelajahi node tetangga (node yang langsung terhubung ke node sumber), kemudian bergerak menuju node tetangga di layer berikutnya. BFS menggunakan queue dalam penggunaannya. Dengan BFS, kita dapat memiliki banyak kegunaan seperti kita dapat melakukan pencarian maupun mencari shortest path dari suatu graph.

-
void Graph::BFS(int s) { // Mark all the vertices as not visited bool *visited = new bool[V]; for(int i = 0; i < V; i++) visited[i] = false; // Create a queue for BFS list<int> queue; // Mark the current node as visited and enqueue it visited[s] = true; queue.push_back(s); // 'i' will be used to get all adjacent // vertices of a vertex list<int>::iterator i; while(!queue.empty()) { // Dequeue a vertex from queue and print it s = queue.front(); cout << s << " "; queue.pop_front(); // Get all adjacent vertices of the dequeued // vertex s. If an adjacent has not been visited, // then mark it visited and enqueue it for (i = adj[s].begin(); i != adj[s].end(); ++i) { if (!visited[*i]) { visited[*i] = true; queue.push_back(*i); } } } }
Untuk implementasi menggunakan adjacency list, silakan dibuat sendiri, gunakan C++ STL. BFS menghasilkan jarak terpendek dari source ke destination jika diterapkan pada unweighted graph.
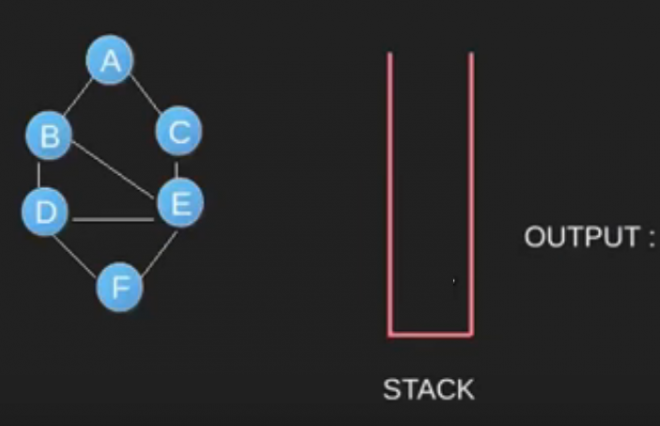
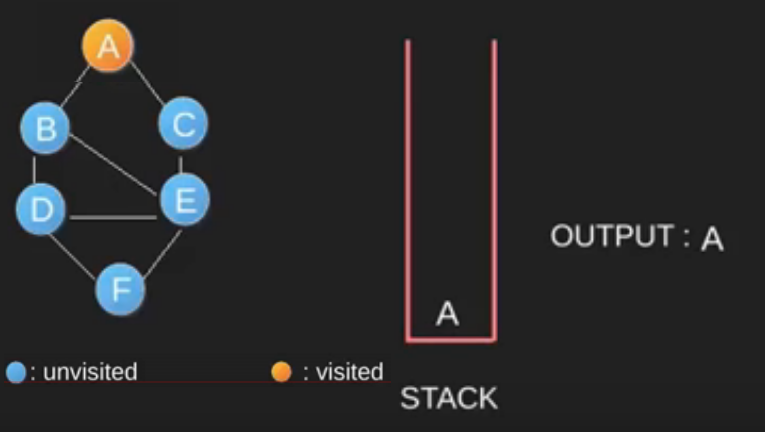
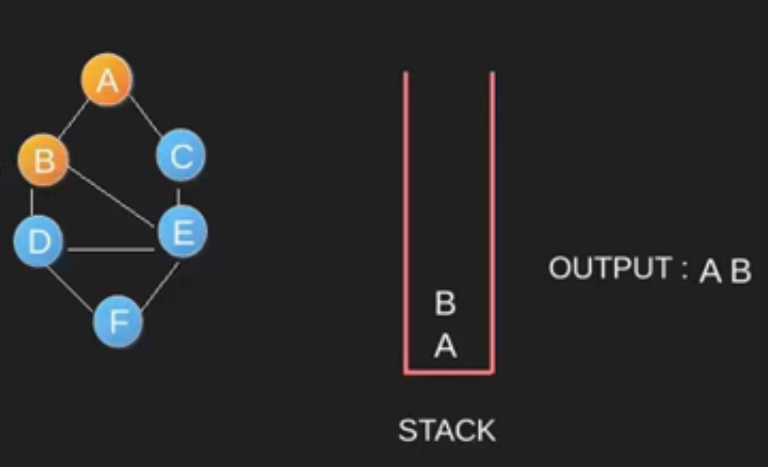
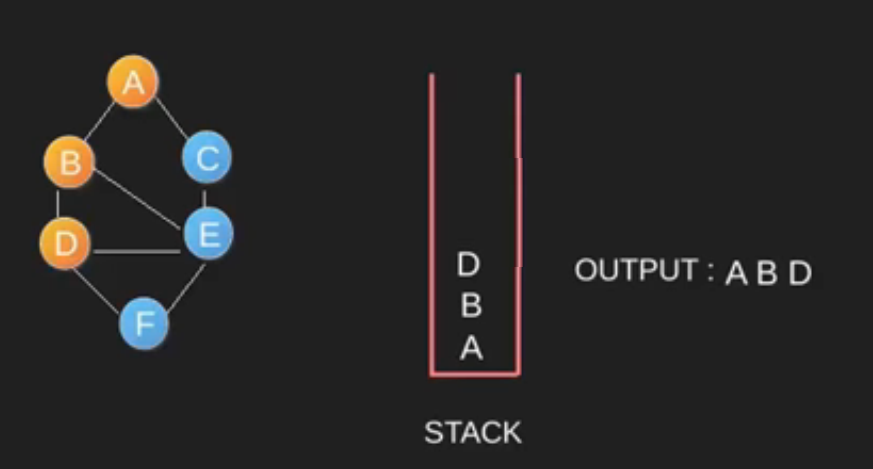
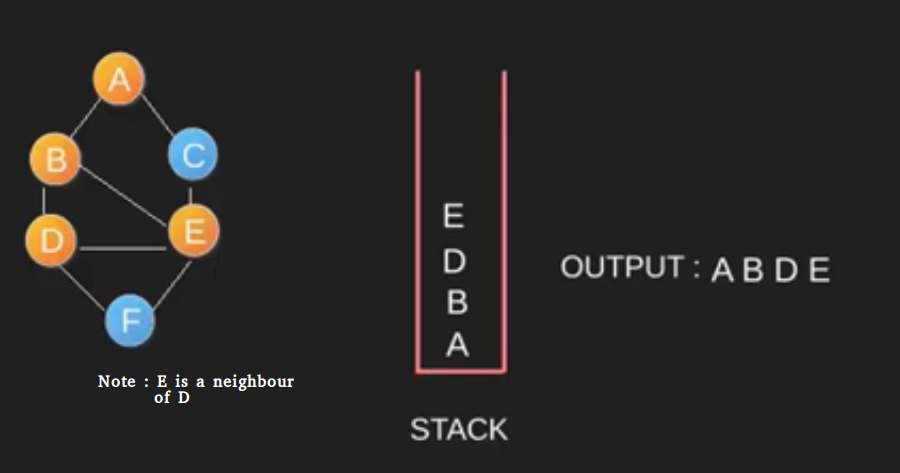
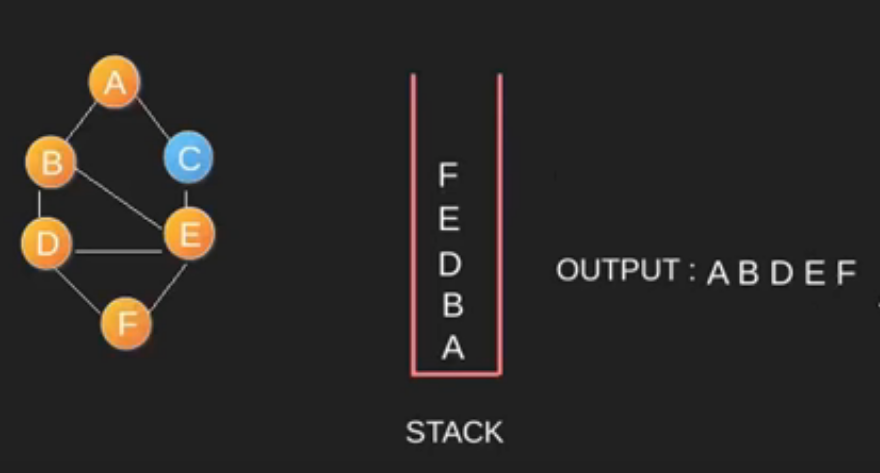
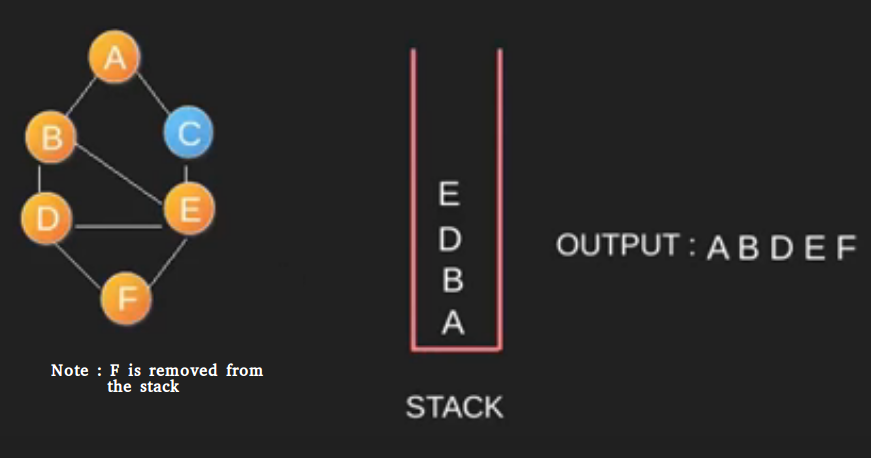
Algoritma DFS adalah algoritma rekursif yang menggunakan gagasan backtracking. Di sini, kata backtrack berarti bahwa ketika Anda bergerak maju dan tidak ada lagi node di sepanjang jalur saat ini, maka Anda akan bergerak mundur di jalur yang sama untuk menemukan node untuk dilintasi. Semua node akan dikunjungi di jalur saat ini sampai semua node yang belum dikunjungi telah dilalui setelah jalur berikutnya akan dipilih. DFS menggunakan stack / rekursif dalam penggunaannya.

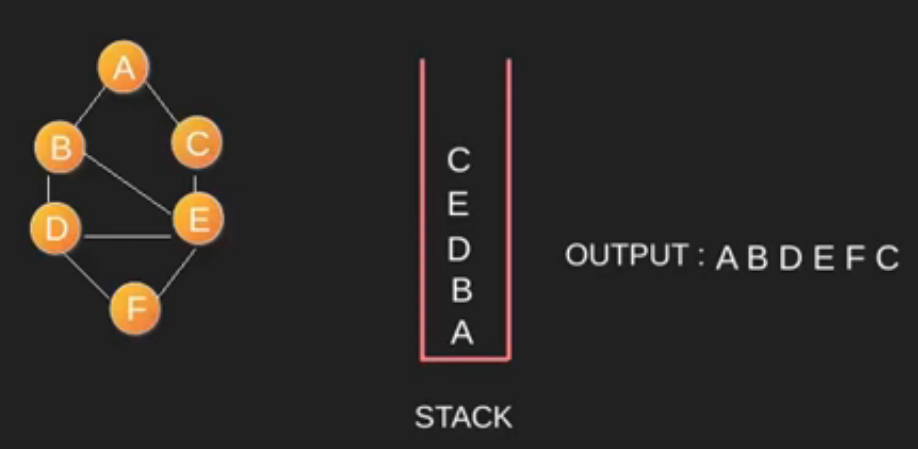
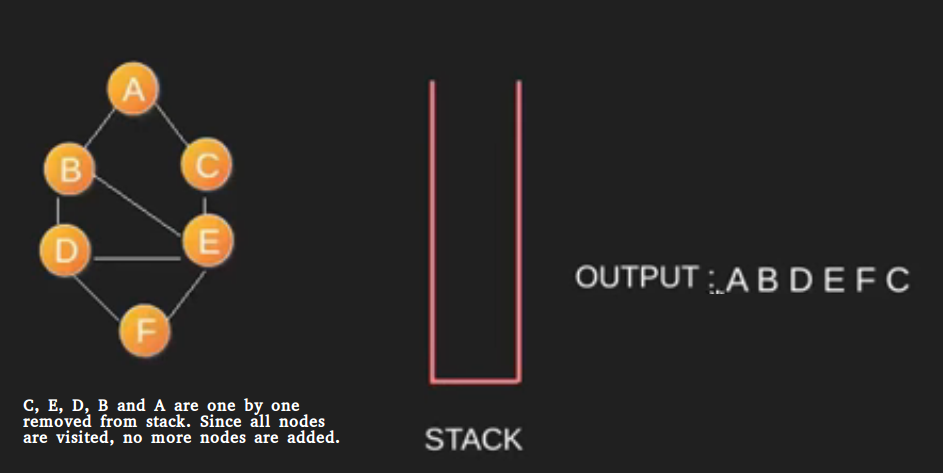
-
void Graph::DFSUtil(int v, bool visited[]) { // Mark the current node as visited and // print it visited[v] = true; cout << v << " "; // Recur for all the vertices adjacent // to this vertex list<int>::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFSUtil(*i, visited); } // DFS traversal of the vertices reachable from v. // It uses recursive DFSUtil() void Graph::DFS(int v) { // Mark all the vertices as not visited bool *visited = new bool[V]; for (int i = 0; i < V; i++) visited[i] = false; // Call the recursive helper function // to print DFS traversal DFSUtil(v, visited); }
Untuk implementasi menggunakan adjacency list, silakan dibuat sendiri, gunakan C++ STL. DFS tidak selalu menghasilkan jarak terpendek dari source ke destination jika diterapkan pada graph.
Misalkan terdapat sebuah graph G yang merupakan undirected weighted graph, maka Spanning Tree merupakan sebuah subgraph dari G dimana semua vertex dapat dikunjungi dan tidak terdapat cycle pada graph tersebut.
Minimum Spanning Tree merupakan Spanning Tree yang memiliki cost paling minimum di antara semua Spanning Tree. Cost yang dimaksud adalah jumlah weight dari semua edge yang ada pada tree tersebut. Memungkinkan untuk terdapat lebih dari 1 Minimum Spanning Tree.
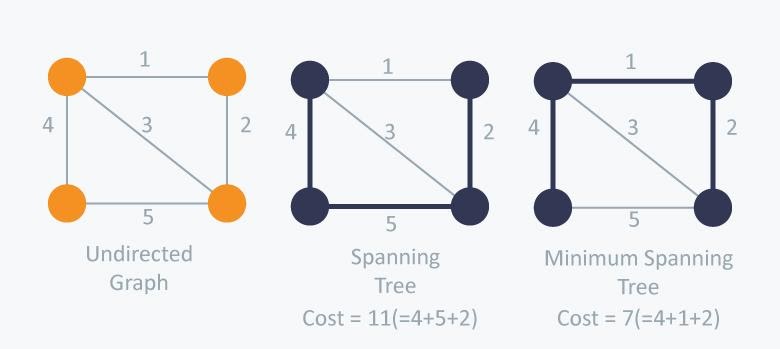
Terdapat 2 implementasi yang terkenal untuk mengimplementasikan Minimum Spanning Tree, yaitu Kruskal’s Algorithm dan Prim’s Algorithm. Namun yang akan kita bahas saat ini adalah Kruskal’s Algorithm.
Algoritma Kruskal menambahkan edge satu per satu sehingga menjadi Spanning Tree. Algoritma Kruskal merupakan pendekatan greedy di mana pada setiap iterasi mencari edge dengan weight terkecil untuk ditambahkan sehingga dapat membentuk Spanning Tree.
Pada Algoritma Kruskal, untuk mendapatkan Minimum Spanning Tree, berikut merupakan 3 langkah yang dilakukan:
- Sort secara non-descending (tidak menurun) semua edge berdasarkan weight-nya
- Tambahkan edge dengan weight terkecil. Apabila terjadi cycle pada Spanning Tree, maka hapus edge tersebut. Apabila tidak, tambahkan edge tersebut pada Spanning Tree.
- Lakukan langkah ke-2 hingga terbentuk V – 1 edge pada Spanning Tree.
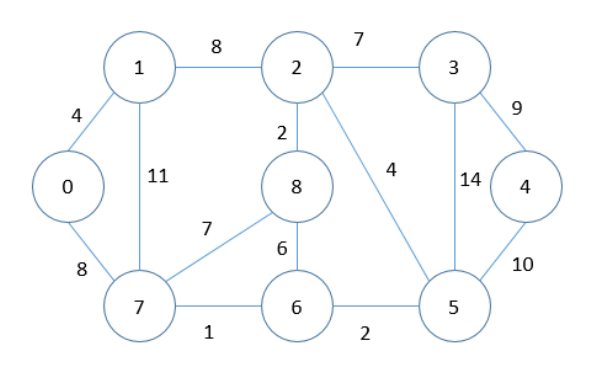 MST = 0
MST = 0
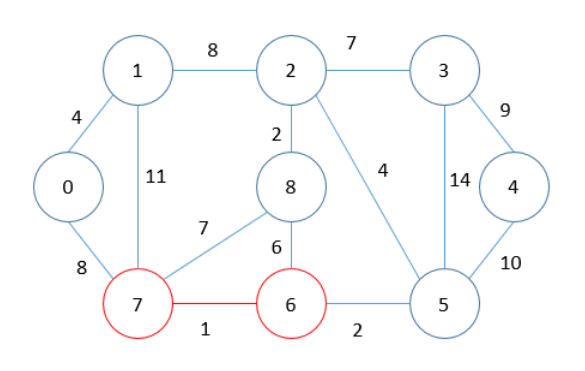 MST = 1
MST = 1
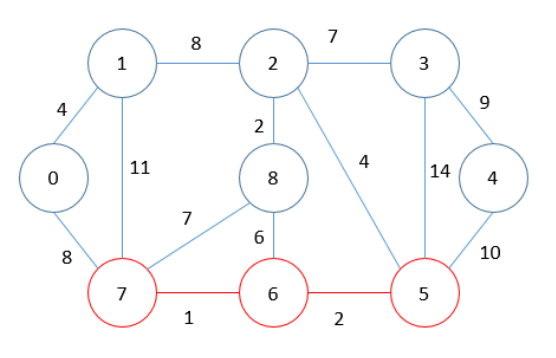 MST = 3
MST = 3
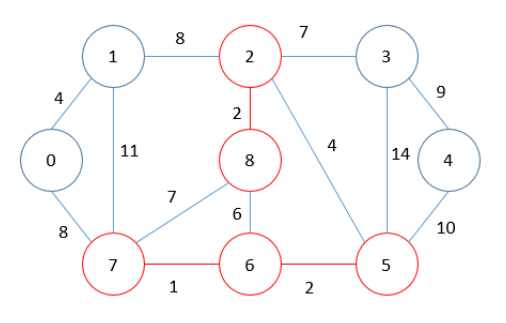 MST = 5
MST = 5
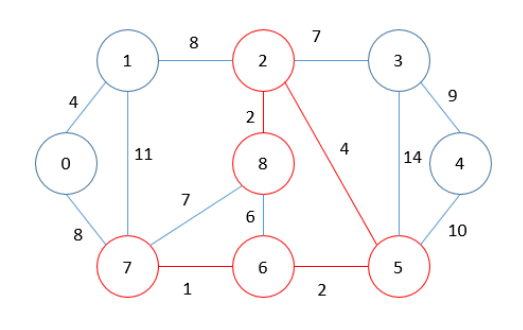 MST = 9
MST = 9
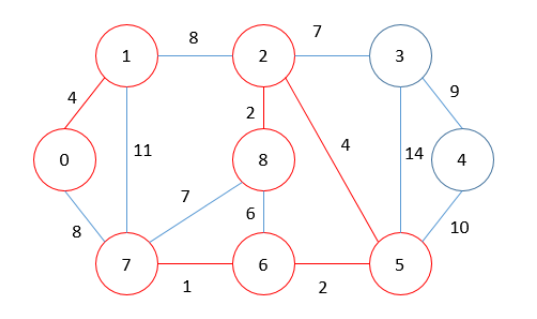 MST = 13
MST = 13
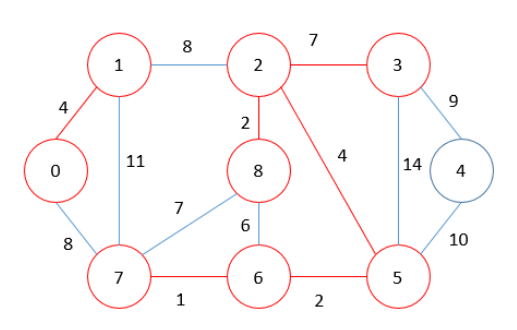 MST = 20
MST = 20
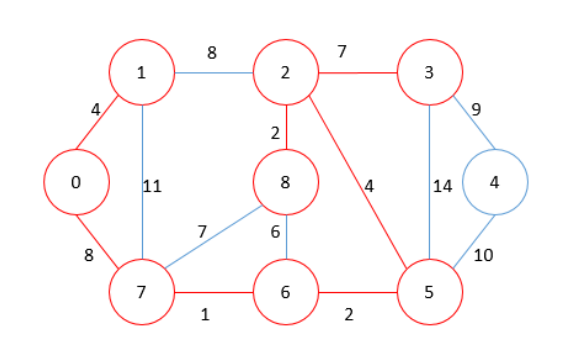 MST = 28
MST = 28
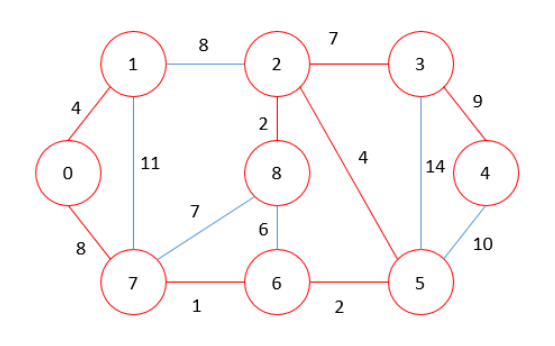 MST = 37
MST = 37
Untuk menentukan apakah penambahan suatu edge dapat menyebabkan cycle, dapat dilakukan disjoint set union (DSU). DSU akan memiliki operasi untuk menggabungkan dua set, dan itu akan dapat menentukan set elemen tertentu. Dengan cara mencari parent dari 2 set yang akan dilakukan pengecekan. Apabila 2 set tersebut memiliki parent yang sama, maka jika dilakukan penambahan edge akan terjadi cycle. Karena itu, edge tidak ditambahkan pada Spanning Tree.
-
Untuk melakukan pencarian parent suatu vertex, kita dapat melakukannya secara iteratif maupun rekursif. Implementasi kali ini menggunakan rekursif.
int find(int x) { if(par[x] != x) { return par[x] = find(par[x]); } return x; }
-
void Kruskal() { int res = 0; for(int i = 0; i < edge.size(); i++) { int src = edge[i].src; int dst = edge[i].dst; int w = edge[i].w; int parSrc = find(src); int parDst = find(dst); // Disjoint Set if(parSrc != parDst) { res += w; par[parSrc] = par[parDst]; } } cout << res << endl; return; }
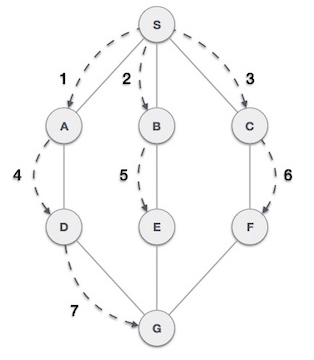
Pada permasalahan graph, Shortest Path Problem merupakan pencarian path dari 2 vertex pada suatu graph yang mempunyai penjumlahan weight yang paling minimum. Permasalahan ini dapat diselesaikan dengan mudah menggunakan BFS apabila semua edge mempunyai weight 1. Namun, pada permasalahan kali ini, weight dapat bernilai berapapun. Terdapat banyak sekali implementasi untuk penyelesaian Shortest Path Problem, tapi yang akan kita bahas saat ini adalah Dijkstra’s Algorithm.
Algoritma Dijkstra sendiri mempunyai banyak variasi, tapi yang paling umum adalah untuk mencari shortest path dari source vertex ke semua vertex lainnya.
- Set semua jarak vertex dengan infinity (dapat digantikan dengan nilai yang sangat besar atau nilai yang tidak akan terpakai) kecuali jarak dari source yang akan di-set 0.
- Push vertex source ke min-priority queue (priority queue dengan pengurutan dari kecil ke besar) dengan format (distance, vertex), untuk pembanding dari min-priority queue akan menggunakan distance dari vertex.
- Pop vertex dengan distance yang paling minimum dari priority queue
- Update distance dari vertex yang terhubung ke vertex yang telah di-pop (vertex dari hasil langkah ke-3) dengan case “distance vertex yang sekarang + edge weight < next vertex distance”, lalu push vertex tersebut.
- Apabila hasil dari pop vertex tersebut telah di visit sebelumnya, maka lakukan continue.
- Lakukan langkah ke-3 sampai ke-5 hingga priority queue kosong.
Cari shortest path dari vertex A ke semua vertex lainnya.
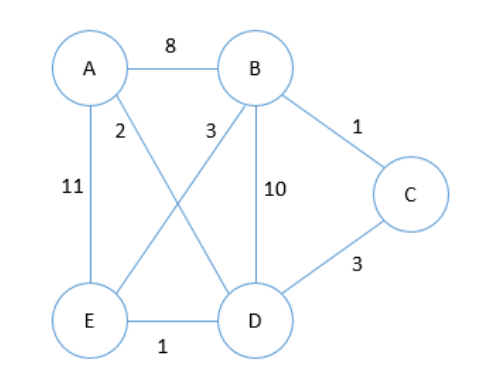
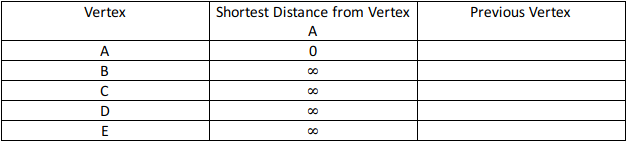
Inisial:
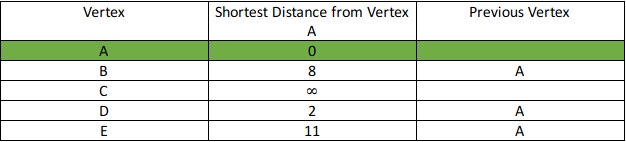
Step 1:
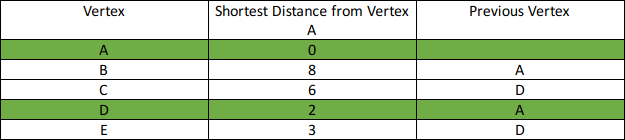
Step 2:
Step 3:
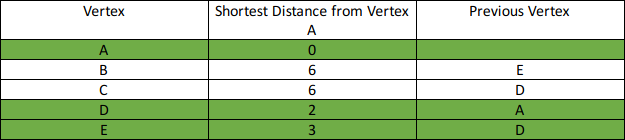
Step 4:
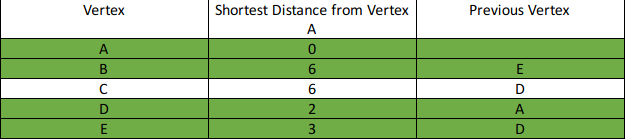
Step 5:
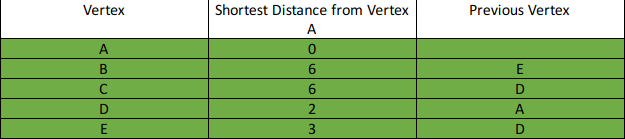
-
// pii pair of integer, integer typedef pair <int, int> pii; int dist[10]; vector <pii> v[10]; void dijkstra(int s, int n) { priority_queue <pii, vector <pii>, greater <pii> > pq; set <int> seen; memset(dist, -1, sizeof(dist)); dist[s] = 0; pq.push({0, s}); while(!pq.empty()) { pii now = pq.top(); pq.pop(); if(seen.find(now.second) != seen.end()) continue; seen.insert(now.second); for(int i = 0; i < v[now.second].size(); i++) { int next = v[now.second][i].second; int cost = v[now.second][i].first; if(now.first + cost < dist[next] || dist[next] == -1) { dist[next] = now.first + cost; pq.push({dist[next], next}); } } } for(int i = 0; i < n; i++) { cout << "from " << s << " to " << i << " : " << dist[i] << endl; } return; }