Distribuições de probabilidades - RuiOrey/Stats-studies GitHub Wiki

#Distribuições de probabilidades univariadas e discretas

###Bernoulli Supondo uma experiência com 2 resultados possiveis: sucesso ou insucesso, sendo que sucesso tem probabilidade p e insucesso 1-p.

Uma variável aleatoria que assume o valor de 1 em caso de sucesso e 0 em caso de insucesso é chamada uma variável aleatoria de Bernoulli - ou diz-se que se trata de uma distribuição de Bernoulli.

Definição As variaveis aleatórias de Bernoulli caracterizam-se da seguinte forma:

Sendo X uma variável aleatória discreta, e o seu suporte (todos os pontos que tem probabiliade positiva de ocorrer) ser Rx = {0,1}.

Sendo também p ∈ (0,1), diz-se que X tem uma distribuição de Bernoulli com parametero p se a sua função de probabiliade é

Na função acima, qualquer indicador(variavel aleatoria que assume o valor 1 se um evento de X ocorre e 0 se não) é uma variavel aleatoria Bernoulli.

Valor esperado E[X] = p

Variância Var[X] = p(1-p)

Função de distribuição Bernoulli

Relação entre a distribuição Bernoulli e a binomial A soma das variaveis aleatorias independentes de Bernoulli é uma variavel aleatoria binomial.

###Distribuição binomial Considerando novamente uma experiência com dois resultados possiveis: sucesso ou insucesso. Suponha-se que essa experiência é repetida várias vezes e que os resultados são independentes entre si. O numero de vezes em que a experiência foi um sucesso é uma variável aleatória cuja distriuição se diz binomial.

Esta distribuição, tem dois parameteros, n, numero de repetições da experiência e p, a probabilidade de uma experiência isolada.

Pode ser vista como a soma das experiências individuais Bernoulli mutuamente independentes que assumem o valor 1 para o caso de sucesso e 0 caso contrário.

Definição A distribuição de Bernoulli caracteriza-se da seguinte forma:

Sendo X uma variável aleatória discreta e n ∈ ℕ e p ∈ (0,1). Sendo o suporte(conjunto de pontos amostrais cuja probabilidade de ocorrer é positiva) de X :

Rx={0,1,..,n}

Diz-se que X tem uma distribuição binomial com parâmetros n e p se a sua funçao de distribuição é:

onde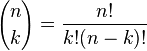 é um coeficiente binomial.

Relação com a distribuição de Bernoulli

A distribuição binomial está relacionada com a distribuição de Bernoulli. As seguintes proposições mostram como.

Proposição Se uma variável aleatória X tem uma distribuição binomial com parameteros n e p, com n=1, então X é uma distribuição de Bernoulli com parameteros p.

Proposição Se uma variavel aleatoria X tem uma distribuição binomial com parameteros n e p, então X é uma soma de n variaveis aleatorias de Bernoulli juntas e independentes com parametero p.

Valor esperado E[X] = np

Variancia Var[X] = np(1-p)

Função de distribuição |arranjar gráfico|

Poisson

A distribuição de Poisson é relacionada com a distribuição exponencial. Suponha-se que um dado evento pode ocorrer varias vezes num determinado intervalo de tempo. Quando o total de ocorrencias do evento é desconhecido, podemos pensar nele como uma variavel aleatoria. Esta variavel aleatoria tem distribuição de Poisson se e só se a o tempo que ocorreu entre um evento e o outro tiver distribuição exponencial e é independente de ocorrencias anteriores.

Um exemplo classico de distribuição de Poisson é um call center. Se o tempo entre duas chamadas sucessivas tiver uma distribuição exponencial e se for independente do tempo de chegada de chamadas anteriores, então o numero total de chamdas recebidas numa hora tem distribuição de Poisson.

No gráfico acima, quer-se mostrar isso. O numero de chamadas recebidas é mostrado como uma função do tempo. O gráfico dá um salto cada vez que uma chamada chega.

O tempo entre duas chamadas é igual ao cumprimento de cada segmento horizontal e tem distribuição exponencial. O numero de chamdas recebidas em 60 minutos é igual ao cumprimento do segmento ilustrado na figura com as chavetas verticais e tem distribuição de Poisson.

Definição Tendo o parametero λ (unidade inversa ao tempo), sendo N(t) o numero de eventos que ocorrem até uma data t.

Ou seja, o numero de eventos que ocorrem até uma data t é um processo de Poisson com parametero λt.

Valor esperado E[X]=λ

Variancia Var[X]=λ

#Distribuições de probabilidades univariadas e continuas

###Exponencial Quanto tempo vai passar antes de acontecer um terramoto numa dada região? Quanto tempo é necessário esperar até que um cliente entre na loja? Quanto tempo demora um call center a receber uma chamada?

Este tipo de questões normalmente são respondidas em termos probabilisticos usando uma distribuição exponencial.

O tempo X que necessitamos de esperar até que um evento ocorra tem distribuição exponencial se a probabilidade que ele ocorra num determinado intervalo é propocional ao cumprimento desse intervalo. Mais especificamente, X tem uma distribuição exponencial se a probabilidade condicionada,

P(t < X ≤ t + Δt | x > t)

for aproximadamente proporcional ao cumprimento Δt do intervalo de tempo enquadrado entre t e t+Δt, para qualquer t. Esta propriedade é muitas vezes verificada em fenomenos reais e por isso, muito usada para modelar tempos de espera.

Além disso, esta medida também se relaciona com a distribuição de Poisson. Quando o evento pode ocorrer mais de uma vez e o tempo decorrido entre as duas ocorrencias sucessivas é exponencialmente distribuido e independente de ocorrencias passadas, o numero de ocorrencias do envento dentro de um dado intervalo tem distribuição de Poisson.

Definição A distribuição exponencial é caracterizada da seguinte forma:

Sendo X uma variavel aleatoria continua e univariada, sendo o seu suporte o conjunto de numero reais

Rx= [0,∞)

Sendo λ ∈ ℝ_+_+. Diz-se que X tem uma distribuição exponencial com parametro λ se a sua função densidade probabilidade for:

fX(x)= λ.e^(-λx) se x ∈ Rx, 0 caso contrario

Valor esperado

E[X] = 1/λ

Variancia

Var[X] = 1/λ²

Propriedade sem memória da distribuição exponencial

###Distribuição Normal A distribuição normal, ou distribuição de Gauss, é das distribuições mais comuns em teoria de probabilidades e estatistica, devido ao papel que desempenha no Teorema do Limite Central e pelo facto que muitos fenomenos do mundo real se representam por uma distribuição normal (ex: erros em medições cientificas).

Chama-se de Gauss(matematico alemão que viveu entre 1777 e 1855) e que deu contribuições importantes para esta distribuição.

Também se refere a ela como a distribuição com forma de sino, porque o gráfico da sua função densidade aparenta um sino. Como se pode ver na figura acima, a densidade é simetrica à volta da média. Em consequencia disso, desvios da média, tendo a mesma magnitude mas sinais diferentes, tem a mesma probabilidade.

A densidade torna-se muito pequena longe da media e muito grande próxima da mesma. Isto significa que, quanto mais longe um valor estiver do centro da distribuição, menor é a sua probabilidade de observação.

Ir-se-á analisar o caso de média 1 e variancia 0, e depois casos de media e variancia genéricos.

####A distribuição normal estandardizada Definição Deixando X ser uma variavel aleatoria continua. O seu suporte (valores possiveis) é o conjunto dos numeros reais.

Diz-se que X tem uma distribuição normal estandardizada se a sua função de densidade de probabilidade for TODO: corrigir para formula normal standard Valor esperado E[X]=0

Variância Var[X]=1

####A distribuição normal em geral Definiçaão Deixando X ser uma variavel aleatoria continua. O seu suporte (valores possiveis) é o conjunto dos numeros reais.

Diz-se que X tem uma distribuição normal com media μ e variancia σ² se a sua função densidade de probabilidade for

**Relação entre desvio padrão geral e estandardizado

A proposição seguinte dá a ligação entre o desvio padrão standard e geral:

Se X tem uma distribuição normal com média μ e variancia σ², então: X = μ + σZ

onde Z é uma variavel aleatória com uma distribuição normal estandardizada.

Valor esperado E[X] = μ

Variancia Var[X] = σ²

Distribuição Chi-quadrado

Uma variavel aleatoria X tem distribuição Chi-quadrado se for uma soma de quadrados de variaveis aleatorias com distribuição normal

X= Y1² + Y2² + ... + YN²

Onde Y1,Y2...YN são variaveis aleatórias com distribuições normais. A importancia desta distribuição vem do facto que este tipo de somas ocorre em estatistica, especialmente na estimação de variancia e testes de hipoteses.

Definição

Sendo X uma variavél aleatoria discreta continua, dizemos que X tem distribuição Chi-quadrado com n graus de liberdade , sendo n um numero natural, se a sua função de densidade de probabilidade é dada por:

onde Γ(k/2) é a função Gama (extensão da função factorial com o seu argumento reduzido 1. É equivalente a (n-1)! em termos genéricos).

Usa-se a notação seguinte para indicar que uma variavél aleatória tem distribuição Chi-quadrado:

Valor esperado E[X] = n

Variancia Var[X] = 2n

O gráfico acima mostra a variação de n de 1 para 2. Constata-se que aumentando os graus de liberdade, aumenta-se a densidade de probabilidade de valores mais altos. A média também se desloca.

Algumas regras:

A soma dos quadrados de duas distribuições normais estandardizada é uma variavel aleatoria chi-quadrada
O quadrado de uma variavel aleatoria normal é uma variavel aleatoria chi-quadrada

Gamma

A ditribuição gama pode ser vista como uma generalização da distribuição chi-quadrado. Se uma variavél aleatória Z tem uma distribuição chiquadrada com n graus de liberdade e h é uma constante positiva, então a variável aleatória X é definida como:

X = h/n * Z

isto define uma distribuição Gamma com parametros n (graus de liberdade) e h (constante).

Definição TODO

Valor esperado E[X] = h Variancia Var[X] = 2 h²/n

Regras

A distribuição Gamma é uma distribuição chi-quadrada escalada - se n = h, temos uma distribuição chi-quadrada
A uma variavel aleatoria de distribuição Gamma é uma soma de variáveis aleatorias normais ao quadrado
Uma variavel aleatoria Gamma vezes uma constante positiva é uma variavél Gamma aleatória

t-Student

Uma distribuição t é uma distribuição que deriva da estimação da média de uma distribuição normal com tamanho amostral pequeno e o desvio padrão é desconhecido.

O unico parametero desta distribuição é os graus de liberdade.

Enquanto uma distribuição normal descreve toda a população, uma distribuição Gamma descreve uma amostra. Para cada tamanho diferente de população, o t-Student é diferente.

Quando maior a amostra, mais a distribuição t-Student se aproxima de uma distribuição normal.

É muito usado para descobrir a significancia estatistica da diferenca de duas médias amostrais, com o teste t-Student, construir intervalos de confiança para a diferença entre duas medias da populaçao e em analise de regressão.

Pode ser escrita como o ratio

sendo Z uma distribuição normal e V uma distribuição chi-quadrada com v graus de liberdade (distribuição Gamma).

Também existe a distribuição t não standard.

t-Student estandardizada

Esta distribuição é um caso particular da distribuição t-Student. Explicando o caso particular, depois será mais facil partir para um caso mais genérico. Definição Sendo B uma distribuição Beta e n os graus de liberdade, a distribuição t-Student tem função densidade de probabilidade

Normalmente o numero de graus de liberdade é inteiro mas pode ser real.

Relação com a distribuição Gamma Uma variavel aleatoria t-Student pode ser escrita como uma variavel aleatoria normal cuja variancia é reciproca de uma variavel aleatoria Gamma (1/Var(XGamma)).

Valor esperado E[X]=μ

Variancia É considerada bem definida para n>2 e é igual a Var[X] = n/(n-2) . σ²

t-Student genérica

Definiçao TODO

Valor esperado E[X]=0

Variancia É considerada bem definida para n>2 e é igual a Var[X] = n/(n-2)

O autor denominou-se de Student porque na altura em que a publicou trabalhava na cervejaria Guiness, que o impedia de publicar.

Convergencia para distribuição normal - uma distribuição t-Student com media μ, escala σ² e n graus de liberdade, converge em distribuição para uma distribuição normal com média μ, desvio padrão σ² quando n se torna largo e converge para o infinito.

F

Uma variavel aleatoria tem distribuição F se pode ser escrita como o ratio

em que U1 e U2 são distribuições chi-quadradas independentes e d o seu grau de liberdade.

Definição TODO

Valor esperado E[X] = n2/(n2-2)

Variancia A variancia de X está bem definida só para n2 > 4 e é igual a

Var[X] = (2N² . (n1 + n2 - 2)) / n1(n2-2)²(n2-4)