Background

Closed loop control allows the robot to control itself, responding to external influence without requiring driver input. In the context of the 2015 robot, closed loop control will be used to maintain the robot at a given pose angle (orientation of robot with respect to the field).

A standard PID controller will be used to correct for errors between the desired robot pose angle (from driver input) and the actual pose angle (from gyro sensor).

PID Control Theory

A PID controller is a flexible algorithm which, after proper tuning, converts an error between an actual and desired measurement to a control effort which will correct for that error. A properly tuned PID can quickly correct for sudden changes in the error, as well as small errors that exist in steady-state.

PID stands for Proportional, Integral, Derivative controller. Its output is computed by taking the sum of three terms:

• The error in the current loop
  • AKA "Proportional"
• The change in the error from the last loop to the current loop
  • AKA "Derivative"
• The sum of all previous error values in each loop
  • AKA "Integral"

Each term is scaled by a constant (P, I, and D). These three constants are the tuning "knobs" that the developer uses to match the controller to the physical system (the robot).

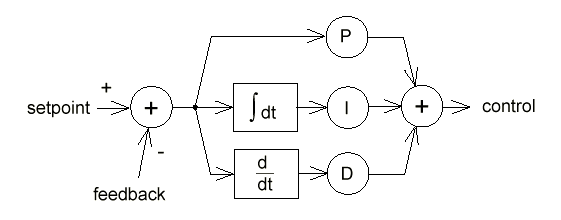
In the context of the 2015 robot, the inputs and outputs are as follows:

• Setpoint = Desired Pose Angle
  • Determined from driver input
• Feedback = Actual Pose Angle
  • Determined from Gyro sensor
• Control = Amount of angle correctional effort required to eliminate the angle error
  • Will have to be mapped to motor values to achieve proper rotation

Robot-Centric Control Derivation

To properly leverage PID control, a more general derivation of the mapping from driver input and sensor input to motor outputs is required.

Be sure to review the drivetrain model for information on the robot physical configuration.

Definitions

We start by positioning an axis over the robot, and define all angles according to this axis:

We then define variables as follows:

• M1-M3 = Controllable motor outputs
• = Actual angle from the robot 0 degree line to some line parallel with the field centerline.
  • Derived from gyro sensor
• = desired angle from the robot 0 degree axis to some line parallel with the field centerline.
  • Derived from adding up all previous and current values of the driver's right joystick, and multiplying by some constant to control maximum rotation rate.
• = Desired angle of travel with respect to the robot's reference axis
  • Derived from driver's left joystick angle
• = Desired robot speed
  • Derived from how far the driver's left joystick is pushed away from the center position (in any direction)

Derivation

We assume there are three components of motion to consider for our drivetrain:

• 1 Effort required to traverse in a given direction
• 2 Effort required to rotate in a given direction
• 3 Effort required to counteract unwanted rotation during traversal

1 will be a function of the desired velocity, and the desired angle of travel.

2 will be a function of the required error corrective effort. This effort is calculated by the PID algorithm, and is a function of the error between desired and actual angle.

3 Will also be a function of the desired velocity and desired angle of travel.

Note that, for a very good PID algorithm, component 3 may not be required, as the PID algorithm would handle correcting for the unwanted error. However, since the PID does not take input from the desired velocity or angle of travel, all traversal will induce non-zero error at first. To help out the closed loop algorithm, we introduce component three so that, if properly configured, very little to no error in pose angle will be introduced by sideways traversal.

Experimenting with the drivetrain has shown that the robot angle lags the desired angle by an observable amount. This causes difficulty in the driver's ability to accurately position the robot. There have been a few suggested remedies. These should be tried in order:

• 1 Add non-zero Feed-Forward to the PID loop.
  • 'Feed-Forward' adds some amount of the control effort (not the error) directly to the output
  • We will feed forward the driver's right joystick X axis
  • This is desirable since we know apriori that when the stick is pushed in some direction, the robot should rotate in that direction
  • The feed-forward acts as an "assist" to the PID algorithm to correct for known changes in setpoint
• 2 When driver right stick returns to center, set setpoint to current gyro reading
  • Drivers tend to stop rotation once the robot is positioned properly.
  • If the robot position lags the setpoint, the setpoint will always be too far ahead of where the driver wanted it.
  • Resetting the setpoint will (hopefully) make control more intuitive
• 3 If all else fails, disable the PID control during rotation, and re-initialize to zero-state after rotation is complete.

With all sign conventions defined, we now can define the control equations:

As seen above, we have introduced six new tuning constants, K1-K6.

• K1 and K2 impact how much the PID control effort goes into the left/right motors.
  • They should both be 1, unless there is significant difference between the left/right gearboxes and wheels.
• K3 and K4 determine the amount of corrective effort exerted when attempting to traverse sideways.
  • They should be set to the same as the tuned values from open loop control.
• K5 and K6 determine how much feed-forward effort the right joystick exerts on the rotational effort of the robot