What is fftshift?

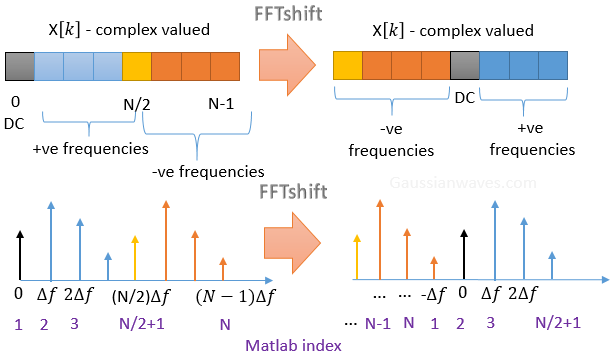
fftshift rearranges a multidimensional discrete Fourier transform, represented by a multidimensional array X, by shifting the zero-frequency component to the center of X.

The following Figure illustrates the fftshift in one dimension.

The following Figure illustrates the fftshift in two dimensions.

The 1D fftshift in CUDA

The code at FFTShift_1D.cu compares 5 different ways to perform the fftshift in the case when the number of elements N is even.

1D CUDA fftshift using memory movements

The first two approaches use memory movements, as in

[1] https://github.com/marwan-abdellah/cufftShift.
[2] M. Abdellah, S. Saleh, A Eldeib, A. Shaarawi, “High performance multi-dimensional (2D/3D) FFT-shift implementation on Graphics Processing Units (GPUs)”, _Proc. of the 6th Cairo Int. Biomed. Eng. Conf._, Cairo, Egypt, Dec. 20-21, 2012, pp. 171-174.

In particular, the first of the memory-movement approaches uses in-place operations, while the second exploits out-of-place operations. The only computational difference between the two is that in-place operations need a temporary variable to swap the two halves of the DFT sequence, while out-of-place operations does not.

1D CUDA fftshift using chessboard multiplication

The other three approaches are based on the following observation.

The Discrete Fourier Transform (DFT) relation is given by

The DFT is thus a periodic sequence of period equal to N and has zero frequency at the k=0 index. Furthermore,

Accordingly, if we want to move the zero frequency to k=N/2, then we have to choose M=N/2, so that

In other words, the zero frequency can be moved to the middle of the sequence through a multiplication of the signal by a chessboard of 1s and -1s in the case when the signal has an even number of elements.

It should be noticed that, in the case of an odd number of elements (which is however not dealt with here), M should be chosen equal to (N-1)/2 so that

Accordingly, in this case, a full multiplication by a complex exponential is needed.

The chessboard multiplication is performed by using cuFFT callback routines.

cuFFT callback routines

Quoting the cuFFT library User's guide,

Callback routines are user-supplied kernel routines that cuFFT will call when loading or storing data. They allow the user to do data pre- or post- processing without additional kernel calls.

Kernel calls indeed have a cost, as underlined in this post, and avoiding them as much as possible is a recommendable programming habit.

Notice that, quoting the static library section of the cuFFT library User's guide

To compile against the static cuFFT library, the following command has to be used:

nvcc myCufftApp.c  -lcufft_static   -lculibos -o myCufftApp\
    -gencode arch=compute_20,\"code=sm_20\"\
    -gencode arch=compute_30,\"code=sm_30\"\
    -gencode arch=compute_35,\"code=sm_35\"\
    -gencode arch=compute_50,\"code=sm_50\"\
    -gencode arch=compute_60,\"code=sm_60\"\
    -gencode arch=compute_60,\"code=compute_60\"

Being the chessboard multiplication needed before the FFT, then the callback routine is of load type.

Note that, again quoting the cuFFT library User's guide concerning the parameters for all of the __device__ load callbacks are defined as below

offset: offset of the input element from the start of output data. This is not a byte offset, rather it is the number of elements from start of data.

dataIn: device pointer to the start of the input array that was passed in the cufftExecute call.

callerInfo: device pointer to the optional caller specified data passed in the cufftXtSetCallback call.

sharedPointer: pointer to shared memory, valid only if the user has called cufftXtSetCallbackSharedSize().

callerInfo and sharedPointer are not used in the considered example.

Performance of the 5 versions of the 1D CUDA fftshift

Testing performed on a GTX 980 card (timing in ms):

N       Out-of-place memory movements   In-place memory movements   Chessboard v1   Chessboard v2   Chessboard v3                    
        _________________________________________________________________________________________________________
    
131072  0.055                           0.057                       0.052            0.182           0.050
524288  0.235                           0.241                       0.191            0.710           0.197
2097152 0.862                           0.872                       0.692            2.715           0.692

As it can be see, a performance gain of about 20/25% can be achieved by the chessboard multiplication approach against the memory movements one.