Knuth–Morris–Pratt algorithm - Maksym-Botvin/study GitHub Wiki

Knuth-Morris and Pratt introduce a linear time algorithm for the string matching problem. A matching time of O (n) is achieved by avoiding comparison with an element of 'S' that have previously been involved in comparison with some element of the pattern 'p' to be matched. i.e., backtracking on the string 'S' never occurs.

Components of KMP Algorithm:

1. The Prefix Function (Π): The Prefix Function, Π for a pattern encapsulates knowledge about how the pattern matches against the shift of itself. This information can be used to avoid a useless shift of the pattern 'p.' In other words, this enables avoiding backtracking of the string 'S.'

2. The KMP Matcher: With string 'S,' pattern 'p' and prefix function 'Π' as inputs, find the occurrence of 'p' in 'S' and returns the number of shifts of 'p' after which occurrences are found.

The Prefix Function (Π)

Following pseudo code compute the prefix function, Π:

COMPUTE- PREFIX- FUNCTION (P)

  1. m ←length [P] //'p' pattern to be matched
  2. Π [1] ← 0
  3. k ← 0
  4. for q ← 2 to m
  5. do while k > 0 and P [k + 1] ≠ P [q]
  6. do k ← Π [k]
  7. If P [k + 1] = P [q]
  8. then k← k + 1
  9. Π [q] ← k
  10. Return Π

Running Time Analysis:

In the above pseudo code for calculating the prefix function, the for loop from step 4 to step 10 runs 'm' times. Step1 to Step3 take constant time. Hence the running time of computing prefix function is O (m).

Example: Compute Π for the pattern 'p' below:

Alt text

Solution:

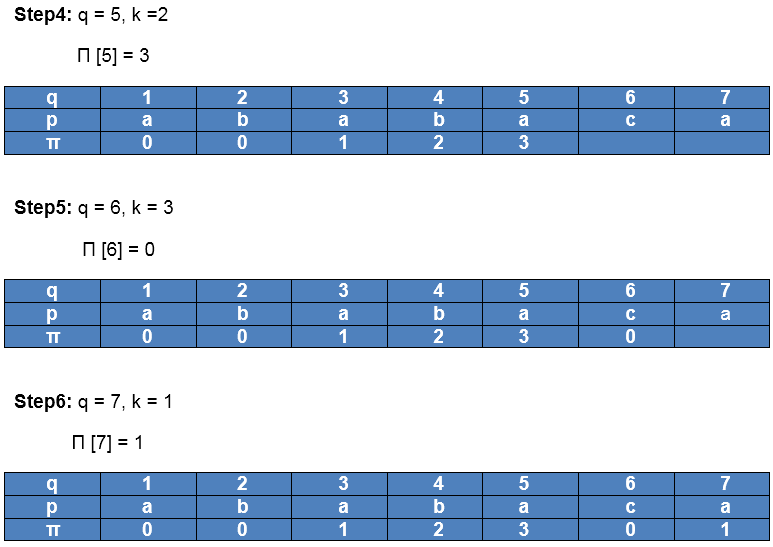
Initially: m = length [p] = 7
    indented Π [1] = 0
    indented k = 0

Alt text Alt text

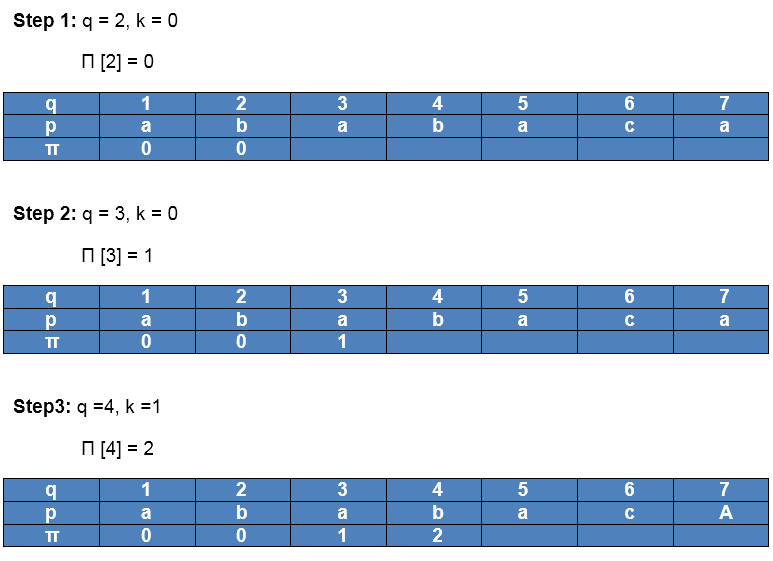
After iteration 6 times, the prefix function computation is complete:

Alt text

The KMP Matcher:

The KMP Matcher with the pattern 'p,' the string 'S' and prefix function 'Π' as input, finds a match of p in S. Following pseudo code compute the matching component of KMP algorithm:

KMP-MATCHER (T, P)

  1. n ← length [T]
  2. m ← length [P]
  3. Π← COMPUTE-PREFIX-FUNCTION (P)
  4. q ← 0 // numbers of characters matched
  5. for i ← 1 to n // scan S from left to right
  6. do while q > 0 and P [q + 1] ≠ T [i]
  7. do q ← Π [q] // next character does not match
  8. If P [q + 1] = T [i]
  9. then q ← q + 1 // next character matches
  10. If q = m // is all of p matched?
  11. then print "Pattern occurs with shift" i - m
  12. q ← Π [q] // look for the next match

Running Time Analysis:

The for loop beginning in step 5 runs 'n' times, i.e., as long as the length of the string 'S.' Since step 1 to step 4 take constant times, the running time is dominated by this for the loop. Thus running time of the matching function is O (n).

Example: Given a string 'T' and pattern 'P' as follows:

Alt text

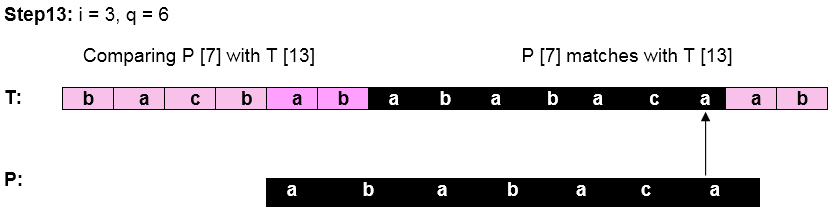
Let us execute the KMP Algorithm to find whether 'P' occurs in 'T.'
For 'p' the prefix function, ? was computed previously and is as follows:

Alt text

Solution:

Initially: n = size of T = 15
m = size of P = 7

Alt text Alt text Alt text Alt text Alt text Alt text

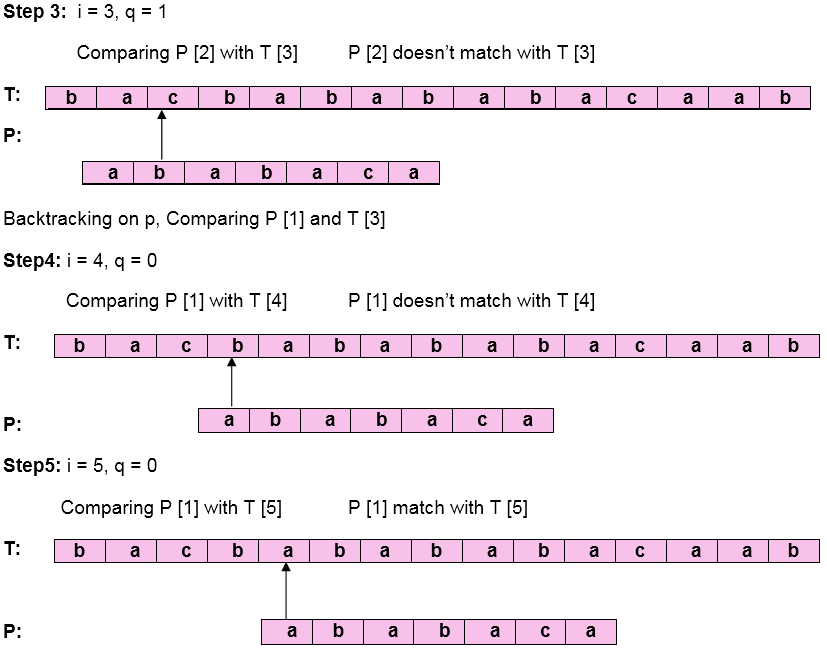
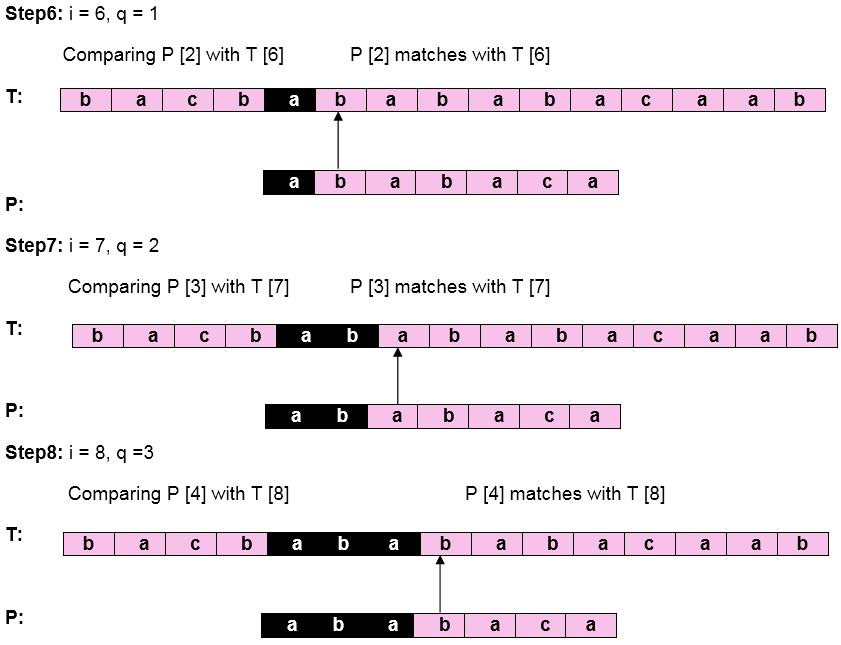
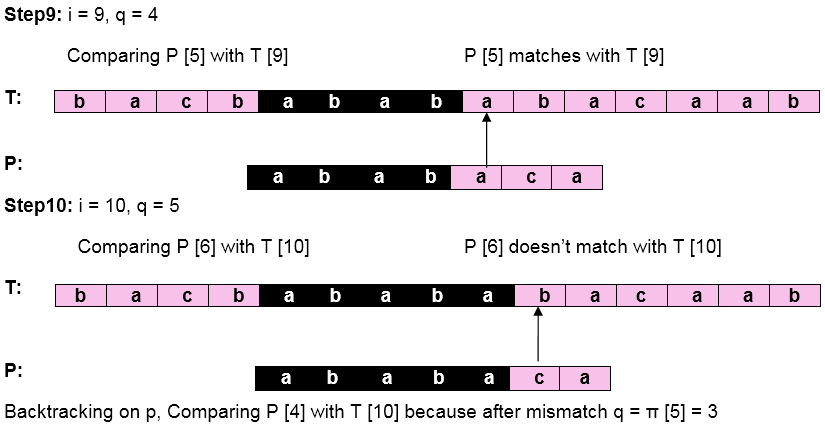
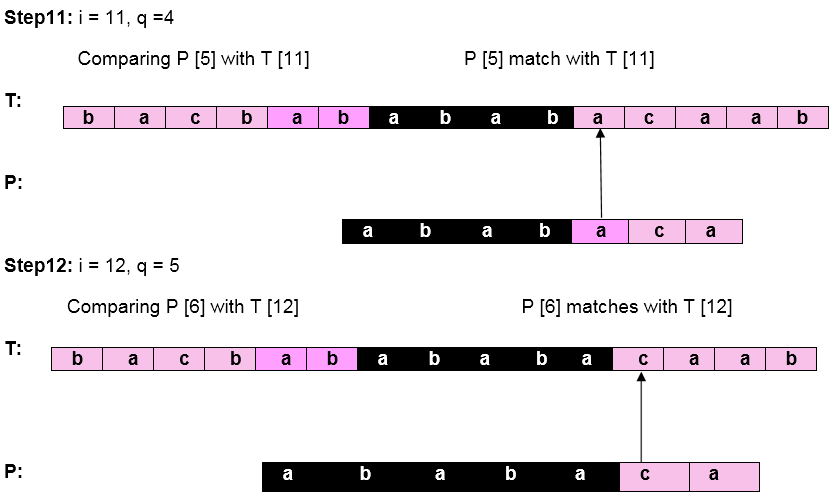
Pattern 'P' has been found to complexity occur in a string 'T.' The total number of shifts that took place for the match to be found is i-m = 13 - 7 = 6 shifts.

The complexity of the Knuth–Morris–Pratt algorithm:

Time Complexity: O(N)
Auxiliary Space: O(M)

JAVA program for implementation of KMP pattern searching algorithm

void KMPSearch(String pat, String txt) {
            int M = pat.length();
            int N = txt.length();

            // create lps[] that will hold the longest
            // prefix suffix values for pattern
            int lps[] = new int[M];
            int j = 0; // index for pat[]

            // Preprocess the pattern (calculate lps[]
            // array)
            computeLPSArray(pat, M, lps);

            int i = 0; // index for txt[]
            while ((N - i) >= (M - j)) {
                if (pat.charAt(j) == txt.charAt(i)) {
                    j++;
                    i++;
                }
                if (j == M) {
                    System.out.println("Found pattern "
                            + "at index " + (i - j));
                    j = lps[j - 1];
                }

                // mismatch after j matches
                else if (i < N
                        && pat.charAt(j) != txt.charAt(i)) {
                    // Do not match lps[0..lps[j-1]] characters,
                    // they will match anyway
                    if (j != 0)
                        j = lps[j - 1];
                    else
                        i = i + 1;
                }
            }
        }

        void computeLPSArray(String pat, int M, int lps[]) {
            // length of the previous longest prefix suffix
            int len = 0;
            int i = 1;
            lps[0] = 0; // lps[0] is always 0

            // the loop calculates lps[i] for i = 1 to M-1
            while (i < M) {
                if (pat.charAt(i) == pat.charAt(len)) {
                    len++;
                    lps[i] = len;
                    i++;
                } else // (pat[i] != pat[len])
                {
                    // This is tricky. Consider the example.
                    // AAACAAAA and i = 7. The idea is similar
                    // to search step.
                    if (len != 0) {
                        len = lps[len - 1];

                        // Also, note that we do not increment
                        // i here
                    } else // if (len == 0)
                    {
                        lps[i] = len;
                        i++;
                    }
                }
            }
        }

        // Driver code
        public static void main(String args[]) {
            String txt = "ABABDABACDABABCABAB";
            String pat = "ABABCABAB";
            new KMP_String_Matching().KMPSearch(pat, txt);
        }
    }

Visual representation of the algorithm:

⚠️ **GitHub.com Fallback** ⚠️