Knuth–Morris–Pratt algorithm - Maksym-Botvin/study GitHub Wiki
Knuth-Morris and Pratt introduce a linear time algorithm for the string matching problem. A matching time of O (n) is achieved by avoiding comparison with an element of 'S' that have previously been involved in comparison with some element of the pattern 'p' to be matched. i.e., backtracking on the string 'S' never occurs.
1. The Prefix Function (Π): The Prefix Function, Π for a pattern encapsulates knowledge about how the pattern matches against the shift of itself. This information can be used to avoid a useless shift of the pattern 'p.' In other words, this enables avoiding backtracking of the string 'S.'
2. The KMP Matcher: With string 'S,' pattern 'p' and prefix function 'Π' as inputs, find the occurrence of 'p' in 'S' and returns the number of shifts of 'p' after which occurrences are found.
Following pseudo code compute the prefix function, Π:
- m ←length [P] //'p' pattern to be matched
- Π [1] ← 0
- k ← 0
- for q ← 2 to m
- do while k > 0 and P [k + 1] ≠ P [q]
- do k ← Π [k]
- If P [k + 1] = P [q]
- then k← k + 1
- Π [q] ← k
- Return Π
In the above pseudo code for calculating the prefix function, the for loop from step 4 to step 10 runs 'm' times. Step1 to Step3 take constant time. Hence the running time of computing prefix function is O (m).
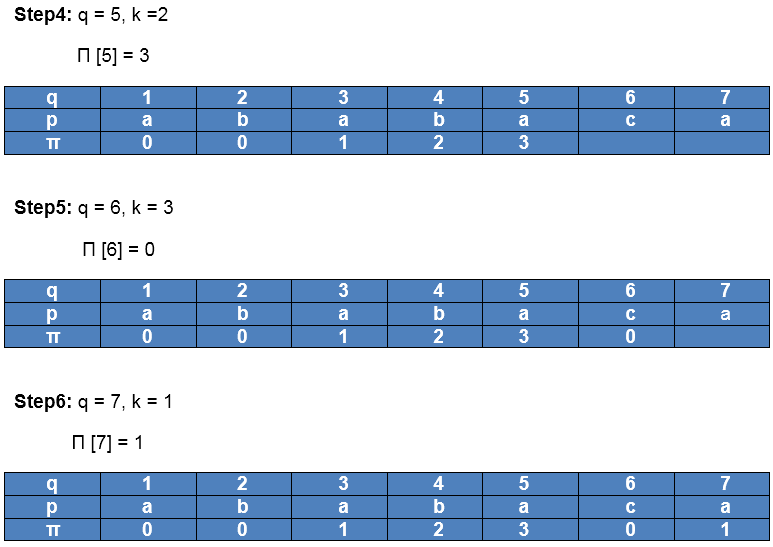
Initially: m = length [p] = 7
indented Π [1] = 0
indented k = 0
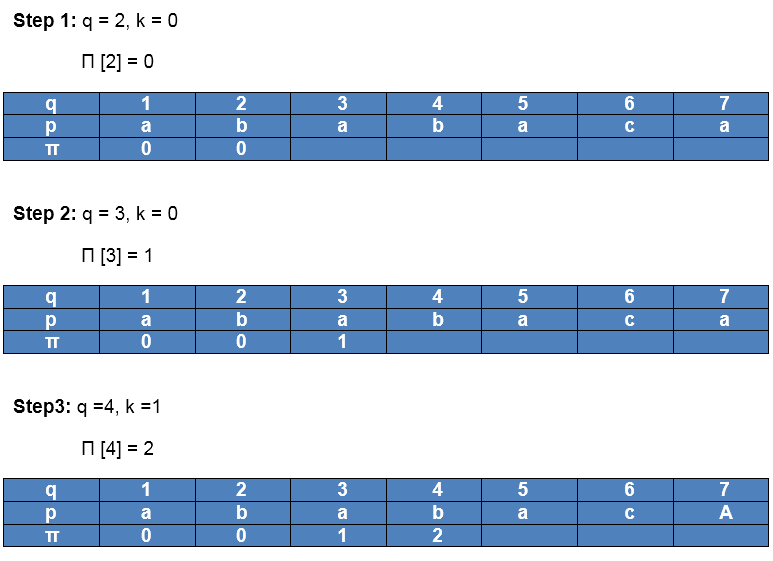
After iteration 6 times, the prefix function computation is complete:
The KMP Matcher with the pattern 'p,' the string 'S' and prefix function 'Π' as input, finds a match of p in S. Following pseudo code compute the matching component of KMP algorithm:
- n ← length [T]
- m ← length [P]
- Π← COMPUTE-PREFIX-FUNCTION (P)
- q ← 0 // numbers of characters matched
- for i ← 1 to n // scan S from left to right
- do while q > 0 and P [q + 1] ≠ T [i]
- do q ← Π [q] // next character does not match
- If P [q + 1] = T [i]
- then q ← q + 1 // next character matches
- If q = m // is all of p matched?
- then print "Pattern occurs with shift" i - m
- q ← Π [q] // look for the next match
The for loop beginning in step 5 runs 'n' times, i.e., as long as the length of the string 'S.' Since step 1 to step 4 take constant times, the running time is dominated by this for the loop. Thus running time of the matching function is O (n).
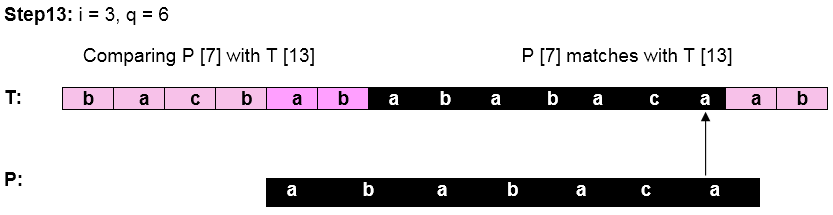
Let us execute the KMP Algorithm to find whether 'P' occurs in 'T.'
For 'p' the prefix function, ? was computed previously and is as follows:
Initially: n = size of T = 15
m = size of P = 7

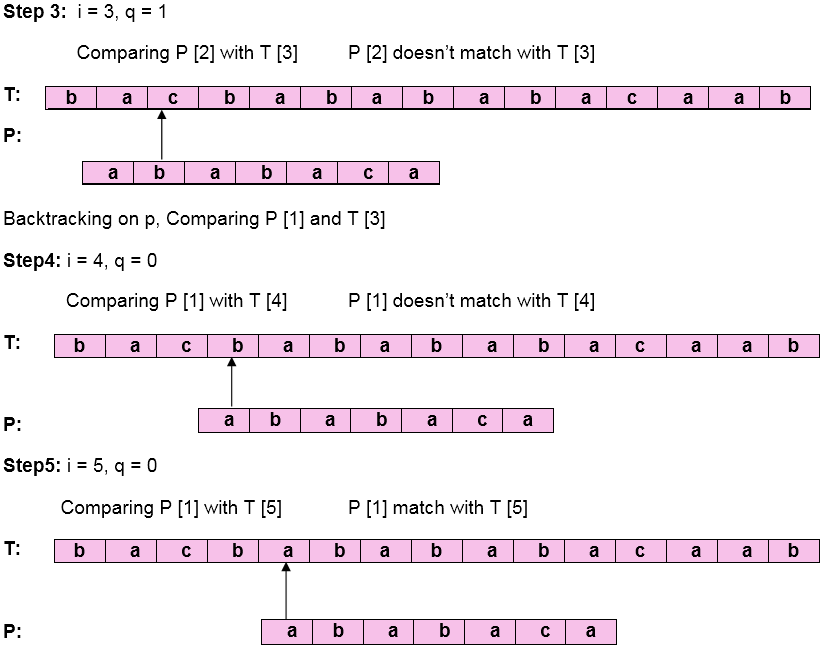
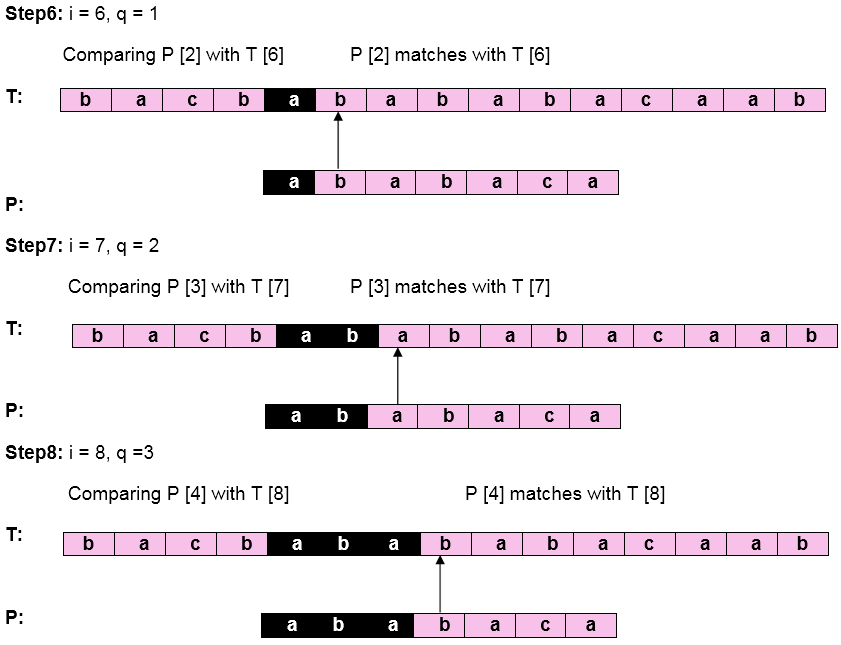
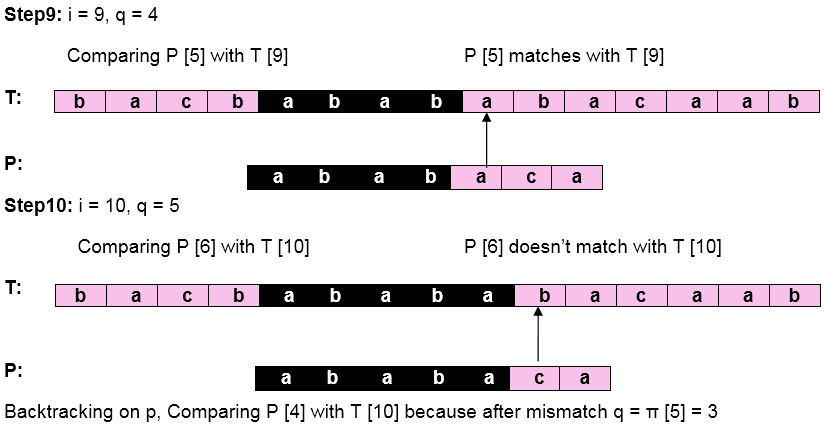
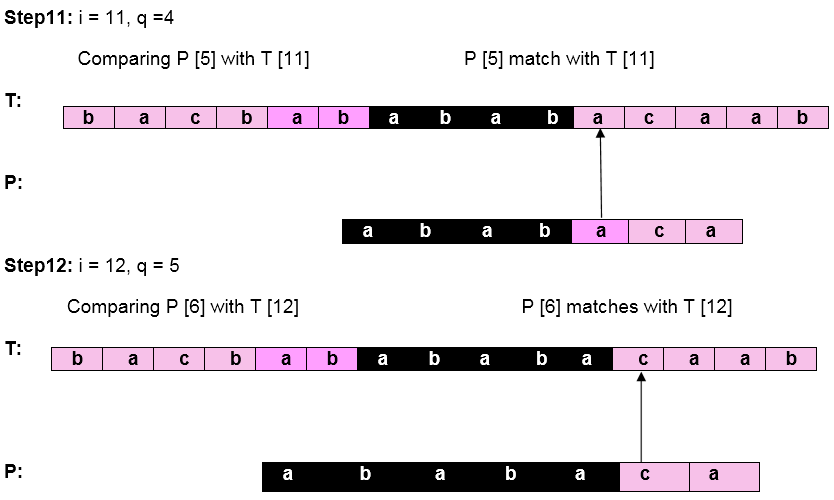
Pattern 'P' has been found to complexity occur in a string 'T.' The total number of shifts that took place for the match to be found is i-m = 13 - 7 = 6 shifts.
Time Complexity: O(N)
Auxiliary Space: O(M)
void KMPSearch(String pat, String txt) {
int M = pat.length();
int N = txt.length();
// create lps[] that will hold the longest
// prefix suffix values for pattern
int lps[] = new int[M];
int j = 0; // index for pat[]
// Preprocess the pattern (calculate lps[]
// array)
computeLPSArray(pat, M, lps);
int i = 0; // index for txt[]
while ((N - i) >= (M - j)) {
if (pat.charAt(j) == txt.charAt(i)) {
j++;
i++;
}
if (j == M) {
System.out.println("Found pattern "
+ "at index " + (i - j));
j = lps[j - 1];
}
// mismatch after j matches
else if (i < N
&& pat.charAt(j) != txt.charAt(i)) {
// Do not match lps[0..lps[j-1]] characters,
// they will match anyway
if (j != 0)
j = lps[j - 1];
else
i = i + 1;
}
}
}
void computeLPSArray(String pat, int M, int lps[]) {
// length of the previous longest prefix suffix
int len = 0;
int i = 1;
lps[0] = 0; // lps[0] is always 0
// the loop calculates lps[i] for i = 1 to M-1
while (i < M) {
if (pat.charAt(i) == pat.charAt(len)) {
len++;
lps[i] = len;
i++;
} else // (pat[i] != pat[len])
{
// This is tricky. Consider the example.
// AAACAAAA and i = 7. The idea is similar
// to search step.
if (len != 0) {
len = lps[len - 1];
// Also, note that we do not increment
// i here
} else // if (len == 0)
{
lps[i] = len;
i++;
}
}
}
}
// Driver code
public static void main(String args[]) {
String txt = "ABABDABACDABABCABAB";
String pat = "ABABCABAB";
new KMP_String_Matching().KMPSearch(pat, txt);
}
}