Algorithms in JavaScript - Lee-hyuna/33-js-concepts-kr GitHub Wiki
인터뷰 절차는 일반적으로 화상으로 시작한 다음 일부 현장에서 코딩 기술 및 문화적으로 적합한지 확인합니다. 거의 예외없이 결정적인 요소는 코딩에 대한 적성입니다. 어쨌든, 엔지니어들은 하루가 끝날 때는 동작하는 소프트웨어를 제공해야 합니다. 전통적으로, 코딩에 대한 적성을 확인하기 위해 화이트보딩을 사용하여 테스트 하였습니다. 정답을 얻는 것 이상으로 사고 과정이 명확하게 표현됩니다. 삶처럼 코드는 정답이 없지만 좋은 추론만으로 충분합니다. 효과적으로 추론하는 능력은 배우고, 적응하고, 발전할 수 있는 잠재력을 나타냅니다. 가장 좋은 엔지니어는 항상 이를 발전시키고, 가장 좋은 회사는 항상 혁신하고 있습니다.
알고리즘 과제가 효과적인 이유는 알고리즘에 대한 해결 방법이 여러가지 있기 때문입니다. 알고리즘 과제는 결정을 내릴 수 있는 가능성과 그 결정들의 미적분학을 열어줍니다. 알고리즘 과제를 해결할 때, 여러 관점에서 문제에 대한 정의를 보고 다양한 접근법의 장점 및 단점을 따져봐야 합니다. 충분한 연습을 통해 완벽한 해결책이 없다는 것 진실을 알게 되기도 합니다.
알고리즘을 진정으로 마스터하는 것은 데이터 구조와 관련하여 이러한 알고리즘을 이해하는 것입니다. 데이터 구조와 알고리즘은 음과 양, 유리잔과 물과 같이 연결 되는 것입니다. 유리잔이 없으면 물을 담을 수 없습니다. 데이터 구조 없이는 로직에 적용되는 대상이 없는 것과 없습니다. 물이 없으면 유리잔은 비어 있고 지탱할 수 없습니다. 알고리즘이 없으면, 대상은 변환될 수 없고, 소비가 되어 질 수 없습니다.
For a quick high-level analysis of Data Structures in JavaScript:
https://medium.com/siliconwat/data-structures-in-javascript-1b9aed0ea17c
코드를 적용되는 알고리즘은 특정 input 데이터 구조를 특정 output 데이터 구조로 변환하는 함수일 뿐이다. 내부적인 로직이 변환을 결정합니다. 무엇보다도, input과 output은 단위 테스트로 명확하게 정의가 되어져야하고 이상적이어야 합니다. 이 문제를 철저히 분석하면 코드를 작성할 필요 없이 자연스럽게 해결책을 제시할 수 있으므로 직면한 문제를 완전히 이해해야합니다.
문제에 대한 도메인을 완전히 파악하면, 솔루션 공간의 브래인스토밍을 시작할 수 있습니다. 필요로 하는 변수는 무엇인가요? 반복 횟수는 얼만큼이고 어떤 종류를 사용할까요? 도움이 될만한 기발한 메소드가 빌트인 되어 있을까요? 고려해야할 케이스가 있을까요? 복잡하게 반복되어진 로직은 어렵게 읽히고 이해하게 됩니다. 헬퍼 함수를 추출하거나 추상화할 수 있는가? 알고리즘은 보통 확장성이 있어야 합니다. input의 크기가 많아지면, 함수는 어떻게 실행되나요? 어떤 캐싱 메커니즘이 있어야하나요? 일반적으로 성능 향상(시간)을 위해 메모리 최적화(공간)을 적극 사용 해야 합니다.
문제를 좀 더 구체적으로 만들려면 다아어그램을 그려야합니다!
솔루션의 높은 수준의 구조가 나타나기 시작하면, 수도코드가 시작될 수 있습니다. 면접관에게 강한 인상을 주기 위해서는 코드를 리팩토링하고 재사용할 수 있는 기회를 살펴보세요. 때로는 비슷한 역할을 하는 함수는 파라미터를 추가하여 결합할 수 있습니다. 다른 경우, 커링을 통한 파라미터 제거가 더 좋습니다. 테스트와 유지보수를 쉽게 하기 위해 퓨어 함수를 유지하여 예측할 수 있게 합니다. 다시 말해 결정의 미적분에서 건축적 및 디자인 패턴을 고려하세요.
명확하지 않은 사항이 있으면 해명을 요청 하세요!
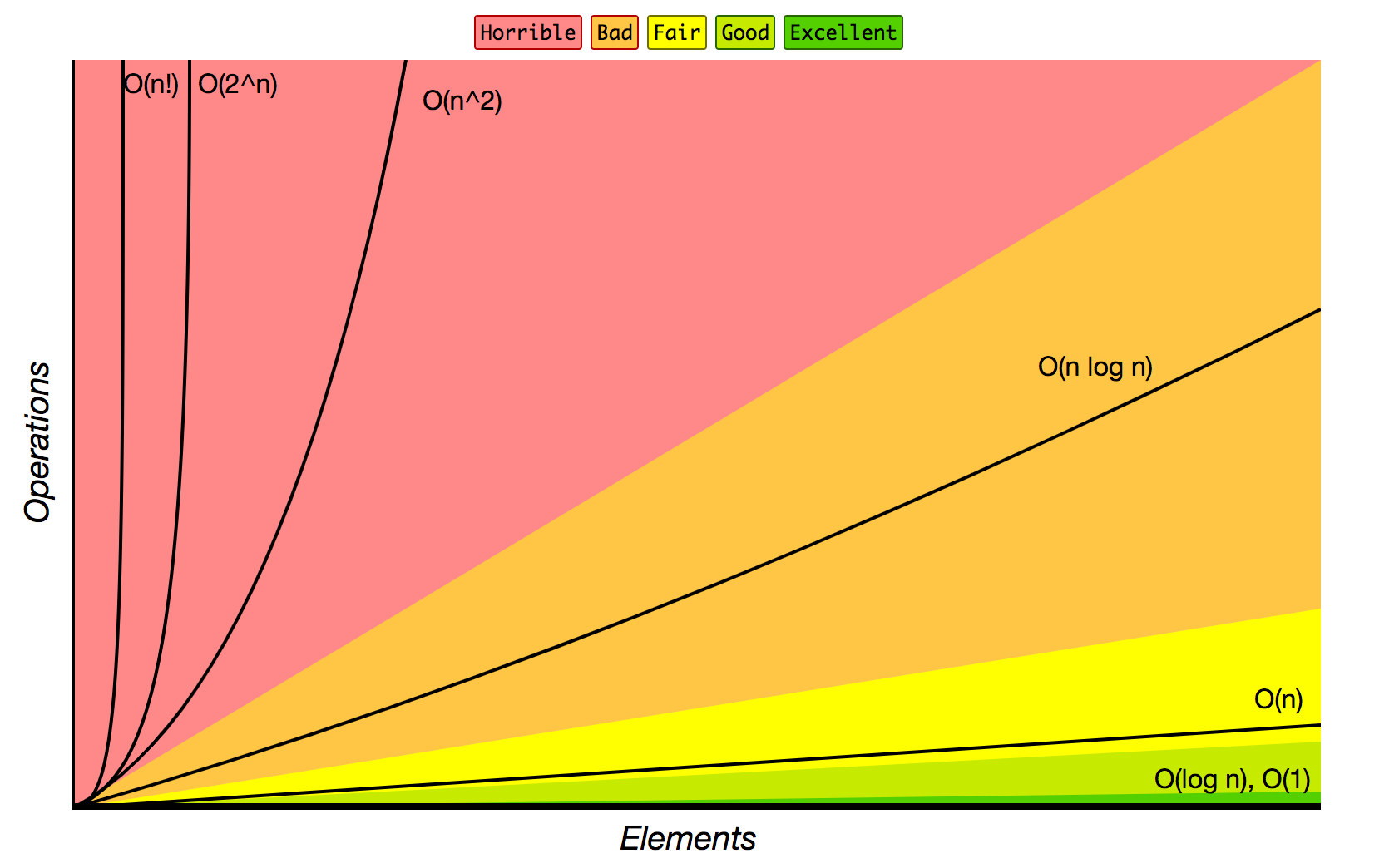
런타임의 복잡도의 미적분을 돕기 위해, 우리는 input의 크기를 무한대로 추정하여 필요한 수의 연산을 계산함으로써 알고리즘의 확장성을 추정합니다. 이 최악의 런타임 상한에서 계수와 덧셈 항을 제거하여 함수를 지배하는 요인만 유지할 수 있습니다. 결과적으로, 몇 가지 범주만으로도 거의 모든 알고리즘의 확장성을 설명할 수 있습니다.
대부분의 최적화된 알고리즘 정수 시간 및 공간으로 스케일을 조정됩니다. 이 것은 그것이 input의 증가에 전혀 신경을 쓰지 않는다는 것을 의미합니다. 다음으로 Logarithmic 시간이나 공간, Linear, Linearithmic, Quadratic 그리고 추가적인 Exponential이 좋다. 가장 나쁜 것은 Factorial 시간이나 공간이다.
Big-O 표기법은 아래와 같다.
- Constant: O(1)
- Logarithmic: O(log n)
- Linear: O(n)
- Linearithmic: O(n log n)
- Quadratic: O(n²)
- Expontential: O(2^n)
- Factorial: O(n!)

Big-O 점근 분석은 알고리즘의 시간과 공간 복잡도 간의 균형을 고려할 때 없어서는 안될 도구입니다. 그러나, Big O는 실제 실행에서 문제가 될 수 있는 경우 일정한 요소를 무시합니다. 또한 시간과 공간을 최적화하면 구현 시간이 늘어나거나 코드 가독성에 부정적인 영향을 줄 수 있습니다. 알고리즘의 구조와 논리를 설계할 때 실제로 무시할 수 있는 것에 대한 직관적인 느낌이 중요합니다.
가장 깨끗한 알고리즘은 일반적으로 언어에 내장된 표준 객체를 이용합니다. 컴퓨터 과학에서 가장 중요한 것은 아마 배열입니다. 자바스크립트에서 배열이 다른 객체보다 더 많은 유틸리티 메소드를 가지고 있습니다. 배열의 메소드 중 기억해야할 배열 메소드는 sort, reverse, slice, splice입니다. 배열 엘리먼트는 0번째 인덱스에서 시작해서 삽입됩니다. 이 뜻은 마지막 엘리먼트는 array.length-1을 의미합니다. 배열은 인덱싱 (push)에 가장 적합하지만 삽입, 삭제(pop 아님) 및 검색 시 위험할 수 있습니다. 자바스크립트에서 배열은 다이나믹하게 발전되어 왔습니다.
Big O에서
- Indexing: O(1)
- Inserting: O(n)
- Deleting: O(n)
- Brute-Force Searching: O(n)
- Optimized Searching: O(log n)
코드에서 배열 메소드의 예제 입니다.
class Arr {
constructor(...items) {
this.arr = new Array(...items);
}
sort(compareFunction) {
return this.arr.sort(compareFunction);
}
reverse() {
return this.arr.reverse();
}
slice(start, end) {
return this.arr.slice(start, end);
}
splice(start, ...params) {
// params = deleteCount, ...items
return this.arr.splice(start, ...params);
}
}
class Str {
constructor(str) {
this.str = new String(str);
}
split(separator, limit) {}
replace(regex_or_substr, substr_or_function) {}
}
mocha.setup("bdd");
const { assert } = chai;
describe("Arrays", () => {
it("Should implement sort", () => {
const arr = new Arr(1, 4, 3, 2, 5);
assert.deepEqual(arr.sort(), [1, 2, 3, 4, 5]);
assert.deepEqual(arr.sort((a, b) => b - a), [5, 4, 3, 2, 1]);
assert.deepEqual(arr.sort((a, b) => a - b), [1, 2, 3, 4, 5]);
const words = new Arr(
{ word: "apple" },
{ word: "orange" },
{ word: "banana" }
);
assert.deepEqual(
words.sort((a, b) => {
if (a.word < b.word) return -1;
if (a.word > b.word) return 1;
return 0;
}),
[{ word: "apple" }, { word: "banana" }, { word: "orange" }]
);
});
it("Should implement reverse", () => {
const arr = new Arr(1, 2, 3, 4, 5);
assert.deepEqual(arr.reverse(), [5, 4, 3, 2, 1]);
});
it("Should implement slice", () => {
const arr = new Arr(1, 2, 3, 4, 5);
assert.deepEqual(arr.slice(), [1, 2, 3, 4, 5]);
assert.deepEqual(arr.slice(1), [2, 3, 4, 5]);
assert.deepEqual(arr.slice(2, 4), [3, 4]);
});
it("Should implement splice", () => {
const arr = new Arr(1, 2, 3, 4, 5);
assert.deepEqual(arr.splice(2, 0, 6), []);
assert.deepEqual(arr.arr, [1, 2, 6, 3, 4, 5]);
assert.deepEqual(arr.splice(3, 1), [3]);
assert.deepEqual(arr.arr, [1, 2, 6, 4, 5]);
assert.deepEqual(arr.splice(2, 1, 3), [6]);
assert.deepEqual(arr.arr, [1, 2, 3, 4, 5]);
assert.deepEqual(arr.splice(0, 2, 6, 7, 8), [1, 2]);
assert.deepEqual(arr.arr, [6, 7, 8, 3, 4, 5]);
assert.deepEqual(arr.splice(arr.arr.length - 3, 2), [3, 4]);
assert.deepEqual(arr.arr, [6, 7, 8, 5]);
assert.deepEqual(arr.splice(-2, 1), [8]);
assert.deepEqual(arr.arr, [6, 7, 5]);
assert.deepEqual(arr.splice(1), [7, 5]);
assert.deepEqual(arr.arr, [6]);
});
});
xdescribe("Strings", () => {
it("Should implement split", () => {})
it("Should implement replace", () => {})
});
mocha.run();
<div id="mocha"></div>(https://codepen.io/thonly/pen/xPGmVX)
MDN에 배열에 대한 자세한 설명이 있습니다.
배열과 비슷한 Sets과 Maps가 있습니다. set에서 아이템은 고유해야합니다. map은 아이템은 사전과 같은 관계에서 key와 value로 구성됩니다.
물론, 객체는 (그리고 리터럴) key와 value 의 쌍으로 저장하는 데 사용할 수 있지만 키는 문자열이어야 한다.
배열과 밀접하게 관련되어 있는 것은 loop을 활용하여 배열을 반복합니다. 자바스크립트에서 반복을 위해 5가지의 제어문을 사용할 수 있습니다. 가장 유명한 것은 거의 모든 순서로 배열 인덱스를 반복하는데 사용하는 변형이 가능한 for loop입니다. 만약 반복 횟수를 결정할 수 없는 경우 특정 조건이 충족될 때까지 while 및 do while loop를 사용할 수 있습니다. 모든 객체에 대해 for in 및 for of loop를 사용하여 key와 value를 반복할 수 있습니다. key와 value를 동시에 얻기 위해서는 entries() 함수를 통해 loop할 수 있습니다. break 문을 사용하면 loop을 빠져나올 수 있고, continue 문을 사용하면 다음 반복문으로 이동할 수 있습니다. 대부분 제어문은 generator함수를 통해 반복하는 것이 가장 효율적입니다.
배열이 가지고 있는 내장 메서드들은 다음과 같습니다. : indexOf, lastIndexOf, includes, fill 그리고 join
또한 배열이 가지고 있는 다음과 같은 메서드에 콜백 함수를 넘길 수 있습니다. : findIndex, find, filter, forEach, map, some, every, and reduce.
아래의 코드는 배열이 가지고 있는 메서드의 사용 예입니다.
class Obj {
constructor(obj) {
this.obj = new Object(obj);
}
indexOf(searchElement, fromIndex = 0) {
for (let i = fromIndex; i < this.obj.length; i++) {
if (this.obj[i] === searchElement) return i;
}
return -1;
}
lastIndexOf(searchElement, fromIndex = this.obj.length - 1) {
for (let i = fromIndex; i >= 0; i--) {
if (this.obj[i] === searchElement) return i;
}
return -1;
}
includes(searchElement, fromIndex = 0) {
let i = fromIndex;
while (i < this.obj.length) {
if (this.obj[i++] === searchElement) return true;
}
return false;
}
fill(value, start = 0, end = this.obj.length - 1) {
let i = start;
do this.obj[i++] = value;
while (i <= end);
return this.obj;
}
join(separator = ",") {
let str = "";
let i = 0;
for (const value of this.obj) {
++i;
str += value + (i < this.obj.length ? separator : "");
}
return str;
}
findIndex(callback) {
for (const key in this.obj) {
if (callback(this.obj[key], key)) return key;
}
return null;
}
find(callback) {
for (const key in this.obj) {
if (callback(this.obj[key], key)) return this.obj[key];
}
return undefined;
}
filter(callback) {
const obj = {};
for (const key in this.obj) {
if (callback(this.obj[key], key)) obj[key] = this.obj[key];
}
return obj;
}
forEach(callback) {
for (const key in this.obj) {
this.obj[key] = callback(this.obj[key], key);
}
return this.obj;
}
map(callback) {
const obj = {};
for (const key in this.obj) {
obj[key] = callback(this.obj[key], key);
}
return obj;
}
some(callback) {
for (const key in this.obj) {
if (callback(this.obj[key], key)) return true;
}
return false;
}
every(callback) {
for (const key in this.obj) {
if (callback(this.obj[key], key)) continue;
return false;
}
return true;
}
reduce(callback, initialValue) {
let accumulator = initialValue;
for (const key in this.obj) {
accumulator = callback(accumulator, this.obj[key], key);
}
return accumulator;
}
}
mocha.setup("bdd");
const { assert } = chai;
describe("Arrays", () => {
it("Should implement indexOf", () => {
const arr = new Obj(["a", "b", "c"]);
assert.equal(arr.indexOf("b"), 1);
assert.equal(arr.indexOf("e"), -1);
});
it("Should implement lastIndexOf", () => {
const arr = new Obj(["a", "b", "c"]);
assert.equal(arr.lastIndexOf("a"), 0);
assert.equal(arr.lastIndexOf("e"), -1);
});
it("Should implement includes", () => {
const arr = new Obj(["a", "b", "c"]);
assert.equal(arr.includes("c"), true);
assert.equal(arr.includes("e"), false);
});
it("Should implement fill", () => {
const arr = new Obj(["a", "b", "c"]);
assert.deepEqual(arr.fill("e"), ["e", "e", "e"]);
});
it("Should implement join", () => {
const arr = new Obj(["a", "b", "c"]);
assert.equal(arr.join(", "), "a, b, c");
});
});
describe("Objects", () => {
it("Should implement findIndex", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.equal(obj.findIndex((value, key) => value === 2), "b");
assert.equal(obj.findIndex((value, key) => value === 3), null);
});
it("Should implement find", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.equal(obj.find((value, key) => value === 2), 2);
assert.equal(obj.find((value, key) => value === 3), undefined);
});
it("Should implement filter", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.deepEqual(obj.filter((value, key) => value > 0), { a: 1, b: 2 });
assert.deepEqual(obj.filter((value, key) => value > 2), {});
});
it("Should implement forEach", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.deepEqual(obj.forEach((value, key) => value * 2), { a: 2, b: 4 });
});
it("Should implement map", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.deepEqual(obj.map((value, key) => value * 3), { a: 3, b: 6 });
});
it("Should implement some", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.equal(obj.some((value, key) => value > 1), true);
assert.equal(obj.some((value, key) => value > 2), false);
});
it("Should implement every", () => {
const obj = new Obj({ a: 1, b: 2 });
assert.equal(obj.every((value, key) => value > 0), true);
assert.equal(obj.every((value, key) => value > 1), false);
});
it("Should implement reduce", () => {
const obj1 = new Obj({ a: 1, b: 2 });
assert.equal(obj1.reduce((sum, value, key) => sum + value, 0), 3);
const obj2 = new Obj({ a1: { b1: 1, b2: 2 }, a2: { b3: 3, b4: 4 } });
assert.deepEqual(
obj2.reduce((accumulator, value, key) => ({ ...accumulator, ...value }), {}),
{ b1: 1, b2: 2, b3: 3, b4: 4 }
);
});
xit("Should flatten objects", () => {
const flatten = obj => {
if (obj instanceof Obj) {
return obj.reduce(
(accumulator, value, key) =>
Object.assign({}, accumulator, flatten(new Obj(value))),
{}
);
}
return obj;
};
assert.deepEqual(
flatten(
new Obj({
a1: { b1: 1, b2: { c1: 1, c2: 2 } },
a2: { b3: 3, b4: { c3: 3, c4: 4 } }
})
),
{ b1: 1, c1: 1, c2: 2, b3: 3, c3: 3, c4: 4 }
);
});
});
mocha.run();(https://codepen.io/thonly/pen/JOdwKM)
주요 논문에서 Church-Turing Thesis는 모든 반복 함수가 재귀 함수로 구현 할 수 있고, 그와 반대 되는 것도 구현 할 수 있다고 증명하고 있습니다. 때로는, 재귀가 더욱더 세련된 접근을 할 수 있도록 합니다. factorial 함수의 반복을 예로 들어봅니다.
const factorial = number => {
let product = 1;
for (let i = 2; i <= number; i++) {
product *= i;
}
return product;
};아래의 코드는 재귀 함수를 사용하여 한줄의 코드로 표현할 수 있습니다.
const factorial = number => {
return number < 2 ? 1 : number * factorial(number - 1);
};모든 재귀 함수는 공통의 패턴을 공유합니다. 모든 재귀 함수는 자기 자신을 호출하는 재귀 부분과 자기 자신을 호출하지 않는 케이스가 생성되어 구성되어 있습니다. 자기 자신을 함수가 호출될 때마다, 자기 자신을 호출한 함수는 실행 스택에 새로운 실행 컨텍스트에 들어갑니다. 자기 자신을 호출하지 않는 케이스를 만날 때까지 계속되고 컨텍스트가 하나씩 튀어 나오면서 스택이 pop됩니다. 따라서 재귀에 대해 주의하지 않고 의존하게 되면 스택 오버플로 런타임 오류가 발생할 수 있습니다.
factorial 함수의 예시 코드 입니다.
const factorial = number => number < 2 ? 1 : number * factorial(number - 1);
const factorialize = number => {
let product = 1;
for (let i = 2; i <= number; i++) {
product *= i;
}
return product;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Factorial", () => {
it("Should implement factorial", () => {
assert.equal(factorial(0), 1);
assert.equal(factorial(1), 1);
assert.equal(factorial(2), 2);
assert.equal(factorial(3), 6);
assert.equal(factorial(4), 24);
assert.equal(factorial(5), factorialize(5));
});
});
mocha.run();https://codepen.io/thonly/pen/vWXNPN
마지막으로, 모든 알고리즘에 변화를 가지기 시작 했습니다.
이 섹션에서는 난이도에 따라 22가지 자주 묻는 알고리즘 문제를 살펴봅니다. 다른 접근 방식과 그에 따른 장단점 및 런타임의 복잡도에 대해서도 설명합니다. 일반적으로 세련된 솔루션은 특별한 트릭 또는 트릭을 사용하여 해결합니다. 이를 염두해두고 시작하겠습니다.
문자열을 입력 받으면 문자를 뒤집어서 반환하는 함수를 구현하는 문제가 주어 집니다.
describe("String Reversal", () => {
it("Should reverse string", () => {
assert.equal(reverse("Hello World!"), "!dlroW olleH");
});
});분석:
트릭을 알고 있다면, 하찮은 해결방법이다. 그 트릭은 간단하게 배열에 내장되어 있는 reverse 메소드를 사용하면 되는 것입니다. 첫번째로, split 메소드를 사용하여 문자 배열을 생성한 다음 rervese 메소드를 사용하여 뒤집은 후 join 메소드를 사용하여 조합합니다. 이 해결방법은 코드를 1줄로 작성할 수 있습니다. 세련되지 않은 방법이지만 최신 문법 및 헬퍼 메소드를 사용하여 문제를 해결할 수도 있습니다. 모든 문자열의 모든 문자의 반복을 위해 최신 문법인 for of loop을 사용하여 표현할 수 있습니다. 또는 임시 변수를 유지할 필요가 없는 배열의 reduce 메소드를 사용할 수도 있습니다.
문자열을 입력받으면 모든 문자를 한번씩 접근해야할 필요가 있습니다. 이 것은 여러번 발생하지만 시간 복잡도은 lineal로 정규화 됩니다. 별도의 내부 데이터 구조가 유지되지 않기 때문에 공간 복잡도는 일정합니다.
코드:
const reverse = string =>
string
.split("")
.reverse()
.join("");
const _reverse = string => {
let result = "";
for (let character of string) result = character + result;
return result;
};
const __reverse = string =>
string.split("").reduce((result, character) => character + result);
mocha.setup("bdd");
const { assert } = chai;
describe("String Reversal", () => {
it("Should reverse string", () => {
assert.equal(reverse("Hello World!"), "!dlroW olleH");
assert.equal(_reverse("Hello World!"), "!dlroW olleH");
assert.equal(__reverse("Hello World!"), "!dlroW olleH");
});
});
mocha.run();https://codepen.io/thonly/pen/VryYBp
펠린드롬은 단어 또는 구문이 앞에서 읽을 때와 뒤에서 읽을 때의 단어가 같은 것을 말합니다. 이를 확인하는 함수를 작성하세요.
describe("Palindrome", () => {
it("Should return true", () => {
assert.equal(isPalindrome("Cigar? Toss it in a can. It is so tragic"), true);
});
it("Should return false", () => {
assert.equal(isPalindrome("sit ad est love"), false);
});
});분석:
펠린드롬 문제에서 중요한 통찰력은 문자열 뒤집기 문제에서 배운 내용을 기반으로 구축할 수 있다는 것입니다. 예외적으로 boolean값을 반환합니다. 이것은 원래 문자열에 대해 트리플 equal을 검사의 결과값을 반환하는 만큼 간단합니다. 또한 배열의 새로운 every 메소드를 사용하여 첫번째 문자와 마지막 문자가 가운데에서 순차적으로 일치하는지 확인할 수 있습니다. 그러나, 이 것은 필요 이상으로 두 번 더 점검합니다. 문자열 뒤집기 문제와 유사하게 시간과 공간에 대한 런타임 복잡도은 동일합니다.
전체 문구를 테스트하기 위해 함수를 확장하려면 어떻게 해야할까요? 정규 표현식과 문자열의 replace 메소드를 사용하여 문자만 유지하는 헬퍼 함수를 만들 수 있습니다. 만약 정규 표현식이 허용되지 않는다면 필터를 사용하여 허요용 가능한 문자열의 배열을 생성할 수 있습니다.
코드:
const isPalindrome = string => {
const validCharacters = "abcdefghijklmnopqrstuvwxyz".split("");
const stringCharacters = string
.toLowerCase()
.split("")
.reduce(
(characters, character) =>
validCharacters.indexOf(character) > -1
? characters.concat(character)
: characters,
[]
);
return stringCharacters.join("") === stringCharacters.reverse().join("");
};
const _isPalindrome = string =>
string
.split("")
.every((character, index) => character === string[string.length - 1 - index]);
const __isPalindrome = string => {
const cleaned = string.replace(/\W/g, "").toLowerCase();
return (
cleaned ===
cleaned
.split("")
.reverse()
.join("")
);
};
mocha.setup("bdd");
const { assert } = chai;
describe("Palindrome", () => {
it("Should return true", () => {
assert.equal(isPalindrome("Cigar? Toss it in a can. It is so tragic"), true);
assert.equal(
__isPalindrome("Cigar? Toss it in a can. It is so tragic"),
true
);
});
it("Should return false", () => {
assert.equal(isPalindrome("sit ad est love"), false);
assert.equal(_isPalindrome("sit ad est love"), false);
});
});
mocha.run();https://codepen.io/thonly/pen/EwBeKq
정수가 주어지면, 숫자의 순서를 반대로 바꿔주세요.
describe("Integer Reversal", () => {
it("Should reverse integer", () => {
assert.equal(reverse(1234), 4321);
assert.equal(reverse(-1200), -21);
});
});분석:
명확한 트릭은 내장된 toString 메소드를 사용하여 정수를 문자열로 반환하는 것입니다. 그러고 나서 문자열 뒤집기 알고리즘으로 부터의 로직을 간단하게 재사용할 수 있습니다. 숫자를 뒤집은 후 문자열을 숫자로 변환하기 위해 전역 parseInt함수를 사용합니다. 그리고 Math.sign을 사용하여 부호(-,+)를 전달할 수 있습니다. 이를 사용하면 코드를 1줄로 작성할 수 있습니다.
문자열 뒤집기 알고리즘의 로직을 재사용하고, 정수 뒤집기 알고리즘은 시간과 공간에 대한 복잡도는 문자열 뒤집기 알고리즘과 동일합니다.
코드:
const reverse = integer =>
parseInt(
integer
.toString()
.split("")
.reverse()
.join("")
) * Math.sign(integer);
mocha.setup("bdd");
const { assert } = chai;
describe("Integer Reversal", () => {
it("Should reverse integer", () => {
assert.equal(reverse(1234), 4321);
assert.equal(reverse(-1200), -21);
});
});
mocha.run();https://codepen.io/thonly/pen/RjxxZK
숫자를 입력 받으면 1에서 입력 받은 숫자까지 모든 정수를 입력하시오. 그러나 정수는 2로 나누어 떨어지면 "Fizz"를 출력하고, 3으로 나누어 떨어지면 "Buzz"를 출력하시오. 2와 3으로 둘다 나누어 떨어지면 "Fizz Buzz"를 출력하시오.
분석:
나누어 떨어지는지 확인을 위해 % 연산자를 사용하는 것을 깨달았을 때, 고전적인 알고리즘 문제는 쉽게 해결이 가능합니다. %(modulus) 연산자는 두 숫자를 나누고 나머지를 반환합니다. 그러므로, 모든 정수를 loop하여 나머지가 0인 것이 무엇인지 확인할 수 있습니다. 수학에서 숫자를 a와 b로 나눌 수 있는 경우 이 두 수의 최소 공배수로 나눌 수 있음을 생각할 수 있습니다.
코드:
앞서 설명한 알고리즘과 같이 런타임 복잡도는 내부 상태를 유지할 필요가 없으므로 모든 정수에 접근하여 확인하기 때문에 동일합니다.
const fizzBuzz = number => {
let output = [];
for (let i = 1; i <= number; i++) {
if (i % 6 === 0) output.push("Fizz Buzz");
else if (i % 2 === 0) output.push("Fizz");
else if (i % 3 === 0) output.push("Buzz");
else output.push(i);
}
return output;
};
mocha.setup("bdd");
const { assert } = chai;
let output;
describe("Fizz Buzz", () => {
beforeEach(() => (output = fizzBuzz(30)));
it("Should output number", () => {
assert.equal(output[0], 1);
});
it("Should output Fizz", () => {
assert.equal(output[1], "Fizz");
});
it("Should output Buzz", () => {
assert.equal(output[2], "Buzz");
});
it("Should output Fizz Buzz", () => {
assert.equal(output[5], "Fizz Buzz");
});
});
mocha.run();https://codepen.io/thonly/pen/PJgewe
문자열을 입력 받으면, 가장 많이 사용된 문자를 반환하세요.
describe("Max Character", () => {
it("Should return max character", () => {
assert.equal(max("Hello World!"), "l");
});
});분석:
이 문제의 트릭은 문자열을 loop을 통해 각각 문자의 모양을 집계하는 테이블을 만드는 것입니다. 테이블은 characters는 key, counters는 value의 형태의 object literal을 사용하여 생성할 수 있습니다. 그런 다음 테이블을 반복하여 key와 value에 임시의 변수값을 담아뒀다가 counters에서 가장 큰 문자를 찾을 수 있습니다. 두개의 서로 다른 input(문자열 과 문자열 map)을 반복하는 두 개의 개별 loop을 사용하지만 시간 복잡도은 linear입니다. 문자열에서 파생된 것이지만 결국 모든 언어에는 문자수가 유한하기 때문에 문자 map의 크기가 제한되어진 크기에 도달하게 됩니다. 같은 이유로 내부 상태를 유지하더라도 input 문자열이 어떤 형태로 커지더라도 공간 복잡도은 일정합니다. 임시 primitive도 큰 스케일에서 무시될 수 있습니다.
코드:
const max = string => {
const characters = {};
for (let character of string)
characters[character] = characters[character] + 1 || 1;
let maxCount = 0;
let maxCharacter = null;
for (let character in characters) {
if (characters[character] > maxCount) {
maxCount = characters[character];
maxCharacter = character;
}
}
return maxCharacter;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Max Character", () => {
it("Should return max character", () => {
assert.equal(max("Hello World!"), "l");
});
});
mocha.run();https://codepen.io/thonly/pen/qVppxO
애니어그램은 동일한 문자 수를 포함하는 단어 또는 구문입니다. 이것을 체크하는 함수를 생성해봅시다.
describe("Anagrams", () => {
it("Should implement anagrams", () => {
assert.equal(anagrams("hello world", "world hello"), true);
assert.equal(anagrams("hellow world", "hello there"), false);
assert.equal(anagrams("hellow world", "hello there!"), false);
});
});분석:
이 문제의 접근법은 각 입력 문자열의 수를 계산하는 문자 map을 만드는 것입니다. 그런다음 map을 비교하여 동일한 지 확인할 수 있습니다. 문자 map을 생성하는 로직은 더 쉽게 재사용할 수 있도록 helper 함수를 구현하면 됩니다. 조금 더 정확하게 하려면 먼저 input 문자열에서 알파벳이 아닌 문자를 모두 제거한 다음 나머지를 소문자로 만들어야 합니다.
앞에서 살펴본 바와 같이 문자 map에서는 linear 시간 복잡도와 constant한 공간 복잡도가 있습니다. 더 정확하게 말하면, 이 접근법은 두 개의 다른 문자열이 검사되기 때문에 시간에 대해 O(n+m)을 갖습니다. 보다 세련된 접근법으로는 input 문자열을 정렬한 다음 같은지 검사하는 방법 입니다. 그러나 단점은 보통 linear 시간이 필요하다는 것입니다.
코드:
const charCount = string => {
const table = {};
for (let char of string.replace(/\W/g, "").toLowerCase())
table[char] = table[char] + 1 || 1;
return table;
};
const anagrams = (stringA, stringB) => {
const charCountA = charCount(stringA);
const charCountB = charCount(stringB);
if (Object.keys(charCountA).length !== Object.keys(charCountB).length)
return false;
for (let char in charCountA)
if (charCountA[char] !== charCountB[char]) return false;
return true;
};
const _sort = string => string.replace(/\W/g, "").toLowerCase().split("").sort().join("");
const _anagrams = (stringA, stringB) => _sort(stringA) === _sort(stringB);
mocha.setup("bdd");
const { assert } = chai;
describe("Anagrams", () => {
it("Should implement anagrams", () => {
assert.equal(anagrams("hello world", "world hello"), true);
assert.equal(anagrams("hellow world", "hello there"), false);
assert.equal(anagrams("hellow world", "hello there!"), false);
assert.equal(_anagrams("hello world", "world hello"), true);
assert.equal(_anagrams("hellow world", "hello there"), false);
});
});
mocha.run();https://codepen.io/thonly/pen/wPyZGo
주어진 단어나 구문이 있으면 그 안에 있는 총 모음 수의 합을 구합니다.
describe("Vowels", () => {
it("Should count vowels", () => {
assert.equal(vowels("hello world"), 3);
});
});분석:
가장 쉬운 해결 방법은 정규식을 활용하여 모든 모음을 추출한 다음 세는 것입니다. 정규식이 허용되지 않으면 모든 문자를 반복하여 모음과 모음을 비교하여 확이할 수 있습니다. 문자열은 먼저 소문자 여야 합니다. 두 가지 방법 모두 모든 문자를 확인해야하고 임시로 담겨지는 primitive들은 무시할 수 있기 때문에 linear 시간 복잡도와 constant 공간 복잡도를 가집니다.
코드:
const vowels = string => {
let count = 0;
const choices = "aeiou"; // or ['a', 'e', 'i', 'o', 'u']
for (let character of string.toLowerCase())
if (choices.includes(character)) count++;
return count;
};
const _vowels = string => {
matches = string.match(/[aeiou]/gi);
return matches ? matches.length : 0;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Vowels", () => {
it("Should count vowels", () => {
assert.equal(vowels("hello world"), 3);
assert.equal(_vowels("hello world"), 3);
});
});
mocha.run();배열과 사이즈가 주어지면 배열 아이템을 주어진 사이즈 만큼의 배열 목록으로 출력합니다.
describe("Array Chunking", () => {
it("Should implement array chunking", () => {
assert.deepEqual(chunk([1, 2, 3, 4], 2), [[1, 2], [3, 4]]);
assert.deepEqual(chunk([1, 2, 3, 4], 3), [[1, 2, 3], [4]]);
assert.deepEqual(chunk([1, 2, 3, 4], 5), [[1, 2, 3, 4]]);
});
});분석:
이 문제의 확실한 해결방법은 마지막 "chunk"에 대한 참조를 유지하고 배열 아이템을 반복할 때 사이즈를 확인하는 것입니다. 보다 세련된 솔루션은 내장된 slice 함수를 사용하는 것입니다. 이렇게 하면 참조가 필요하지 않아 보다 명확한 코드를 생성할 수 있습니다. 주어진 사이즈의 step만큼 증가하는 while loop 또는 for loop을 사용하여 이 작업을 수행할 수 있습니다. 모든 배열 항목을 한 번에 접근해야 하기 때문에 이러한 알고리즘은 모두 liner 시간 복잡도을 갖습니다. 또한 input 배열에 비례하여 증가하는 "chunk"의 내부 배열이 유지 되기 때문에 liner 공간 복잡도를 갖습니다.
코드:
const chunk = (array, size) => {
const chunks = [];
for (let item of array) {
const lastChunk = chunks[chunks.length - 1];
if (!lastChunk || lastChunk.length === size) chunks.push([item]);
else lastChunk.push(item);
}
return chunks;
};
const _chunk = (array, size) => {
const chunks = [];
let index = 0;
while (index < array.length) {
chunks.push(array.slice(index, index + size));
index += size;
}
return chunks;
};
const __chunk = (array, size) => {
const chunks = [];
for (let i = 0; i < array.length; i += size) {
chunks.push(array.slice(i, i + size));
}
return chunks;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Array Chunking", () => {
it("Should implement array chunking", () => {
assert.deepEqual(chunk([1, 2, 3, 4], 2), [[1, 2], [3, 4]]);
assert.deepEqual(chunk([1, 2, 3, 4], 3), [[1, 2, 3], [4]]);
assert.deepEqual(chunk([1, 2, 3, 4], 5), [[1, 2, 3, 4]]);
assert.deepEqual(_chunk([1, 2, 3, 4], 2), [[1, 2], [3, 4]]);
assert.deepEqual(_chunk([1, 2, 3, 4], 3), [[1, 2, 3], [4]]);
assert.deepEqual(_chunk([1, 2, 3, 4], 5), [[1, 2, 3, 4]]);
assert.deepEqual(__chunk([1, 2, 3, 4], 2), [[1, 2], [3, 4]]);
assert.deepEqual(__chunk([1, 2, 3, 4], 3), [[1, 2, 3], [4]]);
assert.deepEqual(__chunk([1, 2, 3, 4], 5), [[1, 2, 3, 4]]);
});
});
mocha.run();https://codepen.io/thonly/pen/BmYVMM
배열 아이템이 주어지면, 순서대로 뒤집어 주세요.
describe("Reverse Arrays", () => {
it("Should reverse arrays", () => {
assert.deepEqual(reverseArray([1, 2, 3, 4]), [4, 3, 2, 1]);
assert.deepEqual(reverseArray([1, 2, 3, 4, 5]), [5, 4, 3, 2, 1]);
});
});분석:
물론, 확실한 해결방법은 내장된 reverse함수를 사용하는 것입니다. 그러나 이것은 너무나 쉽습니다. 허용되지 않으면 단순히 배열의 절반을 반복하고 시작 부분을 끝부분으로 바꿀 수 있습니다. 즉, 아이템 중 하나를 메모리에 임시 저장해야합니다. 이 요구 사항을 피하기 위해 매칭되는 배열을 비구조화 할당 방식과 함께 사용합니다.
따라서, input 배열의 절반만 접근하지만 Big O는 점진적으로 계수를 무시하므로 시간 복잡도은 여전히 linear 입니다.
코드
const reverseArray = array => {
for (let i = 0; i < array.length / 2; i++) {
const temp = array[i];
array[i] = array[array.length - 1 - i];
array[array.length - 1 - i] = temp;
}
return array;
};
const _reverseArray = array => {
for (let i = 0; i < array.length / 2; i++) {
[array[i], array[array.length - 1 - i]] = [
array[array.length - 1 - i],
array[i]
];
}
return array;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Reverse Arrays", () => {
it("Should reverse arrays", () => {
assert.deepEqual(reverseArray([1, 2, 3, 4]), [4, 3, 2, 1]);
assert.deepEqual(reverseArray([1, 2, 3, 4, 5]), [5, 4, 3, 2, 1]);
assert.deepEqual(_reverseArray([1, 2, 3, 4, 5]), [5, 4, 3, 2, 1]);
});
});
mocha.run();https://codepen.io/thonly/pen/eezgYy
구문이 주어지면 각 단어의 문자 순서를 반대로 바꿉니다.
describe("Reverse Words", () => {
it("Should reverse words", () => {
assert.equal(reverseWords("I love JavaScript!"), "I evol !tpircSavaJ");
});
});분석:
split메소드를 사용하여 개별 단어 배열을 만들 수 있습니다. 그런 다음 각 단어에 대해 문자열 뒤집기 로직을 재사용하여 해당 문자를 뒤집을 수 있습니다. 다른 방법은 각 단어를 역순으로 반복하여 결과를 임시 변수에 저장하는 것입니다. 어느 쪽이든, 우리는 모든 단어 뒤집기를 끝에 저장하기 전에 임시적으로 저장해야 합니다. 모든 문자가 접근되고 필수 임시 변수가 입력 문자열에 비례하여 증가하므로 시간 및 공간 복잡도는 liner입니다.
코드:
const reverseWords = string => {
const wordsReversed = [];
string.split(" ").forEach(word => {
let wordReversed = "";
for (let i = word.length - 1; i >= 0; i--) wordReversed += word[i];
wordsReversed.push(wordReversed);
});
return wordsReversed.join(" ");
};
const _reverseWords = string =>
string
.split(" ")
.map(word =>
word
.split("")
.reverse()
.join("")
)
.join(" ");
mocha.setup("bdd");
const { assert } = chai;
describe("Reverse Words", () => {
it("Should reverse words", () => {
assert.equal(reverseWords("I love JavaScript!"), "I evol !tpircSavaJ");
assert.equal(_reverseWords("I love JavaScript!"), "I evol !tpircSavaJ");
});
});
mocha.run();https://codepen.io/thonly/pen/RjRoYd
구문이 주어지면 단어의 앞글자를 대문자로 변경하시오.
describe("Capitalization", () => {
it("Should capitalize phrase", () => {
assert.equal(capitalize("hello world"), "Hello World");
});
});분석:
한 가지 방법은 모든 문자를 반복하는 것이며, 이전 문자가 space 인 경우toUpperCase를 적용하여 현재 문자를 대문자로 변경하세요 **문자열 리터럴 **은 JavaScript에서 불변이므로 적절한 대문자를 사용하여 입력 문자열을 다시 작성해야합니다. 이 방법을 사용하려면 항상 첫 번째 문자를 대문자로 사용해야합니다. 아마도 더 깔끔한 접근 방식은 입력 문자열을 단어 배열로 '분할'하는 것입니다. 그런 다음 단어를 다시 결합하기 전에이 배열을 반복하고 첫 문자를 대문자로 지정할 수 있습니다. 불변성의 같은 이유로, 우리는 적절한 대문자를 포함하는 임시 배열을 메모리에 보관해야합니다.
코드:
const capitalize = phrase => {
const words = [];
for (let word of phrase.split(" "))
words.push(word[0].toUpperCase() + word.slice(1));
return words.join(" ");
};
const _capitalize = phrase => {
let title = phrase[0].toUpperCase();
for (let i = 1; i < phrase.length; i++)
title += phrase[i - 1] === " " ? phrase[i].toUpperCase() : phrase[i];
return title;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Capitalization", () => {
it("Should capitalize phrase", () => {
assert.equal(capitalize("hello world"), "Hello World");
assert.equal(_capitalize("hello world"), "Hello World");
});
});
mocha.run();https://codepen.io/thonly/pen/NwMvNN
구문이 주어지면 각 문자를 주어진 정수로 알파벳의 위나 아래로 이동하여 변경하세요. 필요한 경우 shifting은 알파벳의 시작 또는 끝으로 다시 감싸야합니다.
describe("Caesar Cipher", () => {
it("Should shift to the right", () => {
assert.equal(caesarCipher("I love JavaScript!", 100), "E hkra FwrwOynelp!");
});
it("Should shift to the left", () => {
assert.equal(caesarCipher("I love JavaScript!", -100), "M pszi NezeWgvmtx!");
});
});분석
먼저, 문자의 이동 결과를 계산하려면 알파벳 문자 배열을 만들어야합니다. 이것은 문자를 반복하기 전에 input 문자열을 소문자로 만들어야한다는 것을 의미합니다. 현재 인덱스을 쉽게 추적하려면 정기적 인 for loop를 사용해야합니다. 반복 당 이동 된 문자가 포함 된 새 문자열을 작성해야합니다. 알파벳이 아닌 문자를 만나면 즉시 솔루션 문자열 끝에 추가하고 continue 문을 사용하여 다음 반복으로 넘어 가야합니다. 주요 핵심은 % 연산자를 사용하여 이동이 26보다 클 때 알파벳 배열의 시작 또는 끝으로 줄 바꿈하는 동작을 모방 할 수 있다는 것을 깨닫는 것입니다. 마지막으로, 전에 원래 문자열에서 대문자를 확인해야합니다. 결과를 솔루션에 추가합니다. input 문자열의 모든 문자에 접근하고 새 문자열을 작성해야하므로이 알고리즘은 시간과 공간이 luner하게으로 복잡합니다.
코드
const caesarCipher = (string, number) => {
const alphabet = "abcdefghijklmnopqrstuvwxyz".split("");
const input = string.toLowerCase();
let output = "";
for (let i = 0; i < input.length; i++) {
const letter = input[i];
if (alphabet.indexOf(letter) === -1) {
output += letter;
continue;
}
let index = alphabet.indexOf(letter) + number % 26;
if (index > 25) index -= 26;
if (index < 0) index += 26;
output +=
string[i] === string[i].toUpperCase()
? alphabet[index].toUpperCase()
: alphabet[index];
}
return output;
};
function _caesarCipher(str, n) {
let result = Array(str.length);
for (let i = 0; i < str.length; i++) {
let code = str.charCodeAt(i);
let lower = "a".charCodeAt(0);
if (code >= lower && code < lower + 26)
code = (code - lower + n) % 26 + lower;
let upper = "A".charCodeAt(0);
if (code >= upper && code < upper + 26)
code = (code - upper + n) % 26 + upper;
result[i] = String.fromCharCode(code);
}
return result.join("");
}
mocha.setup("bdd");
const { assert } = chai;
describe("Caesar Cipher", () => {
it("Should shift to the right", () => {
assert.equal(caesarCipher("I love JavaScript!", 100), "E hkra FwrwOynelp!");
assert.equal(_caesarCipher("I love JavaScript!", 100), "E hkra FwrwOynelp!");
});
it("Should shift to the left", () => {
assert.equal(caesarCipher("I love JavaScript!", -100), "M pszi NezeWgvmtx!");
// assert.equal(_caesarCipher("I love JavaScript!", -100), "M pszi NezeWgvmtx!");
});
});
mocha.run();ransom note가 주어지면 magazine word 단어에서 잘라낸 내용을 만들 수 있는지 확인하세요.
const magazine =
"Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum";describe("Ransom Note", () => {
it("Should return true", () => {
assert.equal(ransomNote("sit ad est sint", magazine), true);
});it("Should return false", () => {
assert.equal(ransomNote("sit ad est love", magazine), false);
});it("Should return true", () => {
assert.equal(ransomNote("sit ad est sint in in", magazine), true);
});it("Should return false", () => {
assert.equal(ransomNote("sit ad est sint in in in in", magazine), false);
});
});분석:
확실한 해결책은 magazine word와 rasom word를 개별 단어의 배열으로 나누고 모든 rasom word를 모든magazine word와 비교하여 확인하는 것입니다. 그러나이 접근 방식은 quadratic 시간 또는 'O (n * m)`으로 확장되며 성능이 떨어집니다. magazine word map을 먼저 만든 다음이 테이블에 대해 각 rasom word를 확인하면 liner 시간을 달성 할 수 있습니다. map 객체에서 테이블 조회가 constant 시간에 발생하기 때문입니다. 그러나 맵 객체를 메모리에 유지하려면 공간 복잡도을 희생해야합니다. 코드에서 이것은 모든magazine word어의 수를 만든 다음이 "해시 테이블"에 올바른 수의 rasom word가 포함되어 있는지 확인합니다.
코드:
const ransomNote = (note, magazine) => {
const magazineWords = magazine.split(" ");
const magazineHash = {};
magazineWords.forEach(word => {
if (!magazineHash[word]) magazineHash[word] = 0;
magazineHash[word]++;
});
const noteWords = note.split(" ");
let possible = true;
noteWords.forEach(word => {
if (magazineHash[word]) {
magazineHash[word]--;
if (magazineHash[word] < 0) possible = false;
} else possible = false;
});
return possible;
};
mocha.setup("bdd");
const { assert } = chai;
const magazine =
"Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum";
describe("Ransom Note", () => {
it("Should return true", () => {
assert.equal(ransomNote("sit ad est sint", magazine), true);
});
it("Should return false", () => {
assert.equal(ransomNote("sit ad est love", magazine), false);
});
it("Should return true", () => {
assert.equal(ransomNote("sit ad est sint in in", magazine), true);
});
it("Should return false", () => {
assert.equal(ransomNote("sit ad est sint in in in in", magazine), false);
});
});
mocha.run();배열이 주어지면 mean, median, mode를 구하세요.
const stat1 = new Stats([1, 2, 3, 4, 4, 5, 5]);
const stat2 = new Stats([1, 1, 2, 2, 3, 3, 4, 4]);
describe("Mean", () => {
it("Should implement mean", () => {
assert.equal(Stats.round(stat1.mean()), 3.43);
assert.equal(Stats.round(stat2.mean()), 2.5);
});
});
describe("Median", () => {
it("Should implement median", () => {
assert.equal(stat1.median(), 4);
assert.equal(stat2.median(), 2.5);
});
});
describe("Mode", () => {
it("Should implement mode", () => {
assert.deepEqual(stat1.mode(), [4, 5]);
assert.deepEqual(stat2.mode(), []);
});
});분석:
난이도 측면에서 숫자 모음의 평균 을 찾는 알고리즘이 가장 쉽습니다. 통계적으로 mean은 콜렉션의 sum 을 size로 나눈 것으로 정의됩니다. 따라서 간단히 배열의reduce 메소드를 사용하여 합계를 계산 한 다음이를 '길이'로 나눌 수 있습니다. 이 알고리즘은 내부 메모리가 필요하지 않고 모든 수를 추가해야하므로 liner 시간 및 constant 공간의 런타임 복잡도을 갖습니다.
컬렉션의 중간을 찾는 알고리즘은 보통 어려움이 있습니다. 먼저 배열을 정렬해야하지만 크기가 짝수이면 두 개의 중간 숫자를 처리하기위한 추가 논리가 필요합니다. 이 경우 두 숫자의 평균을 반환해야합니다. 이 알고리즘은 정렬로 인한 linear 시간 복잡도과 정렬 된 배열을 보유하기 위해 내부 메모리가 필요하기 때문에 liner 공간 복잡도을 갖습니다.
mode 를 찾는 알고리즘이 가장 까다 롭습니다. mode는 가장 자주 나타나는 숫자로 정의되므로 frequency table 을 유지해야합니다. 더 복잡하게하기 위해 모든 값이 같은 횟수로 표시되면 모드가 없습니다. 코드에서 이것은 각 고유 번호의 빈도를 계산하는 해시 맵 을 작성하고이를 반복하여 최대 수 또는 수를 수집해야 함을 의미합니다. 메모리에 보유 된 해시 테이블을 작성하기 위해 모든 수를 계산해야하기 때문에이 알고리즘에는 liner 시간 및 공간 복잡도이 있습니다.
코드
class Stats {
constructor(array) {
this.array = array;
}
static round(value, round = 2) {
return Math.round(value * Math.pow(10, round)) / Math.pow(10, round);
}
mean() {
return this.array.reduce((sum, value) => sum + value, 0) / this.array.length;
}
median() {
const arraySorted = this.array.sort();
return arraySorted.length % 2 === 0
? (arraySorted[arraySorted.length / 2 - 1] +
arraySorted[arraySorted.length / 2]) /
2
: arraySorted[Math.floor(arraySorted.length / 2)];
}
mode() {
const table = {};
this.array.forEach(value => (table[value] = table[value] + 1 || 1));
let modes = [];
let max = 0;
for (const key in table) {
const value = parseFloat(key);
const count = table[key];
if (count > max) {
modes = [value];
max = count;
} else if (count === max) modes.push(value);
}
if (modes.length === Object.keys(table).length) modes = [];
return modes;
}
}
mocha.setup("bdd");
const { assert } = chai;
const stat1 = new Stats([1, 2, 3, 4, 4, 5, 5]);
const stat2 = new Stats([1, 1, 2, 2, 3, 3, 4, 4]);
describe("Mean", () => {
it("Should implement mean", () => {
assert.equal(Stats.round(stat1.mean()), 3.43);
assert.equal(Stats.round(stat2.mean()), 2.5);
});
});
describe("Median", () => {
it("Should implement median", () => {
assert.equal(stat1.median(), 4);
assert.equal(stat2.median(), 2.5);
});
});
describe("Mode", () => {
it("Should implement mode", () => {
assert.deepEqual(stat1.mode(), [4, 5]);
assert.deepEqual(stat2.mode(), []);
});
});
mocha.run();숫자 배열이 주어지면 주어진 합계에 더하는 모든 쌍을 반환하세요. 숫자는 두 번 이상 사용할 수 있습니다.
describe("Two Sum", () => {
it("Should implement two sum", () => {
assert.deepEqual(twoSum([1, 2, 2, 3, 4], 4), [[2, 2], [3, 1]]);
});
});
분석:
확실한 해결책은 동일한 배열의 다른 모든 숫자와 비교하여 각 숫자를 확인하는 중첩 loop을 만드는 것입니다. 주어진 합에 합산되는 것은 쌍으로 솔루션 배열에 푸시 될 수 있습니다. 그러나 이 중첩은 quadratic 시간 복잡도을 야기하며 이는 큰 입력에는 적합하지 않습니다. 영리한 속임수는 입력 배열을 반복 할 때 각 숫자의 대응 부분이 있는지 확인하면서 각 숫자의 "상대 부분"을 포함하는 배열을 유지하는 것입니다. 이러한 어레이를 유지함으로써 공간 효율성을 희생하여 liner 시간 복잡도을 얻습니다.
코드:
const twoSum = (array, sum) => {
const pairs = [];
const store = [];
for (let part1 of array) {
const part2 = sum - part1;
if (store.indexOf(part2) !== -1) pairs.push([part1, part2]);
store.push(part1);
}
return pairs;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Two Sum", () => {
it("Should implement two sum", () => {
assert.deepEqual(twoSum([1, 2, 2, 3, 4], 4), [[2, 2], [3, 1]]);
});
});
mocha.run();describe("Max Profit", () => {
it("Should return minimum buy price and maximum sell price", () => {
assert.deepEqual(maxProfit([1, 2, 3, 4, 5]), [1, 5]);
assert.deepEqual(maxProfit([2, 1, 5, 3, 4]), [1, 5]);
assert.deepEqual(maxProfit([2, 10, 1, 3]), [2, 10]);
assert.deepEqual(maxProfit([2, 1, 2, 11]), [1, 11]);
});
분석:
다시, 우리는 매입 가격과 매도 가격의 가능한 모든 조합을 확인하여 어떤 쌍이 가장 큰 수익을 내는지 확인하는 중첩 loop를 만들 수 있습니다. 기술적으로 구매하기 전에 판매 할 수 없으므로 모든 조합을 확인해야하는 것은 아닙니다. 특히, 주어진 구매 가격에 대해, 우리는 판매 가격에 대한 이전의 모든 가격을 무시할 수 있습니다. 따라서이 알고리즘의 시간 복잡도는 quadratic 보다 낫습니다.
조금 더 생각하면 가격 배열을 통해 하나의 loop 만 사용하여 문제를 해결할 수 있습니다. 주요 통찰력은 판매 가격이 구매 가격보다 낮아서는 안된다는 것을 인식하는 것입니다. 그렇다면 우리는 그 낮은 가격으로 주식을 샀어 야합니다. 코드에서 이는 다음 반복에서 구매 가격을 변경해야 함을 나타 내기 위해 일시적인 boolean을 보유 할 수 있음을 의미합니다. 하나의 loop 만 필요한이 세련된 접근 방식은 liner 시간과 constant 공간 복잡도를 갖습니다.
코드:
function maxProfit(prices) {
let minBuyPrice = prices[0] < prices[1] ? prices[0] : prices[1],
maxSellPrice = prices[0] < prices[1] ? prices[1] : prices[2];
let maxProfit = maxSellPrice - minBuyPrice;
let tempBuyPrice = minBuyPrice;
for (let index = 2; index < prices.length; index++) {
const sellPrice = prices[index];
if (minBuyPrice > sellPrice) tempBuyPrice = prices[index];
else {
const profit = sellPrice - minBuyPrice;
if (profit > maxProfit)
(maxProfit = profit),
(maxSellPrice = sellPrice),
(minBuyPrice = tempBuyPrice);
}
}
return [minBuyPrice, maxSellPrice];
}
mocha.setup("bdd");
const { assert } = chai;
describe("Max Profit", () => {
it("Should return minimum buy price and maximum sell price", () => {
assert.deepEqual(maxProfit([1, 2, 3, 4, 5]), [1, 5]);
assert.deepEqual(maxProfit([2, 1, 5, 3, 4]), [1, 5]);
assert.deepEqual(maxProfit([2, 10, 1, 3]), [2, 10]);
assert.deepEqual(maxProfit([2, 1, 2, 11]), [1, 11]);
assert.deepEqual(maxProfit([2, 3, 1, 5, 4]), [1, 5]);
assert.deepEqual(maxProfit([1, 2, 5, 3, 4]), [1, 5]);
assert.deepEqual(maxProfit([2, 10, 5, 1, 3]), [2, 10]);
});
});
mocha.run();주어진 숫자에 대해 0에서 해당 숫자까지의 모든 소수를 찾으세요.
describe("Sieve of Eratosthenes", () => {
it("Should return all prime numbers", () => {
assert.deepEqual(primes(10), [2, 3, 5, 7]);
});
});describe("Sieve of Eratosthenes", () => {
it("Should return all prime numbers", () => {
assert.deepEqual(primes(10), [2, 3, 5, 7]);
});
});
분석:
처음에는 가능한 모든 숫자를 반복하고 % 연산자를 사용하여 가능한 모든 나눠지는 지를 확인하려는 유혹을받을 수 있습니다. 그러나이 방법이 quadratic보다 시간 복잡성이 더 심하여 매우 비효율적이라고 추측하기 쉽습니다. 고맙게도 geography 발명가 인 Cyrene의 Eratosthenes 도 소수를 식별하는 효율적인 방법을 발명했습니다.
코드에서 첫 번째 단계는 주어진 숫자만큼 큰 배열을 만들고 모든 값을 'true'로 초기화하는 것입니다. 다시 말해, 배열 indexes 는 가능한 모든 소수를 나타내고 시작 부분에 모두 true입니다. 그런 다음 배열 키 보간법 을 사용하여 모든 숫자가 false 인 대상을 지정하여 지정된 숫자의 2에서 제곱근까지 반복하는for loop를 만듭니다. 정의에 따라 정수의 곱은 소수가 될 수 없지만 0과 1은 나누기가 소수에 영향을 미치지 않으므로 무시됩니다. 마지막으로 모든 falsey 값을 필터링하여 모든 소수에 도달 할 수 있습니다.
내부 “해시 테이블”을 유지하기 위해 공간의 효율성을 희생함으로써,이 에라토스테네스의이 seive는 quadratic 또는 'O (n * log (log n))'보다 시간 복잡성이 더 우수합니다.
코드:
const primes = number => {
const numbers = new Array(number + 1);
numbers.fill(true);
numbers[0] = numbers[1] = false;
for (let i = 2; i <= Math.sqrt(number); i++) {
for (let j = 2; i * j <= number; j++) numbers[i * j] = false;
}
return numbers.reduce(
(primes, isPrime, prime) => (isPrime ? primes.concat(prime) : primes),
[]
);
};
mocha.setup("bdd");
const { assert } = chai;
describe("Sieve of Eratosthenes", () => {
it("Should return all prime numbers", () => {
assert.deepEqual(primes(10), [2, 3, 5, 7]);
});
});
mocha.run();주어진 인덱스에서 피보나치 수열을 반환하는 ㅎ마수를 구현하세요.
describe("Fibonacci", () => {
it("Should implement fibonacci", () => {
assert.equal(fibonacci(1), 1);
assert.equal(fibonacci(2), 1);
assert.equal(fibonacci(3), 2);
assert.equal(fibonacci(6), 8);
assert.equal(fibonacci(10), 55);
});
});분석:
피보나치 수는 이전 두 가지의 합이므로 가장 간단한 방법은 재귀를 사용하는 것입니다. 피보나치 시리즈는 처음 두 개가 0과 1 인 것으로 가정합니다. 따라서이 사실을 사용하여 기본 케이스를 만들 수 있습니다. 인덱스가 2보다 큰 경우 피보나치 함수를 호출하여 이전 두 개를 추가 할 수 있습니다. 이 재귀 적 접근 방식은 매우 우아하지만 지수 시간과 liner 공간 복잡도로 인해 비효율적입니다. 모든 함수 호출은 호출 스택에 지수 메모리를 필요로하기 때문에 빠르게 중단됩니다.
우아하지는 않지만 반복적 인 접근 방식이 더 시간 효율적입니다. 주어진 인덱스까지 전체 피보나치 시리즈를 만들기 위해 루프를 사용함으로써 liner 시간과 공간을 달성합니다.
코드:
const fibonacci = element =>
// if (element < 0) throw new Error("Index cannot be negative");
element < 3 ? 1 : fibonacci(element - 1) + fibonacci(element - 2);
const _fibonacci = element => {
const series = [1, 1];
for (let i = 2; i < element; i++) {
const a = series[i - 1];
const b = series[i - 2];
series.push(a + b);
}
return series[element - 1];
};
mocha.setup("bdd");
const { assert } = chai;
describe("Fibonacci", () => {
it("Should implement fibonacci", () => {
assert.equal(fibonacci(1), 1);
assert.equal(fibonacci(2), 1);
assert.equal(fibonacci(3), 2);
assert.equal(fibonacci(6), 8);
assert.equal(fibonacci(10), 55);
assert.equal(_fibonacci(1), 1);
assert.equal(_fibonacci(2), 1);
assert.equal(_fibonacci(3), 2);
assert.equal(_fibonacci(10), 55);
});
});
mocha.run();피보나치 시리즈에 대한 성능 재귀 함수를 구현하십시오.
describe("Memoized Fibonacci", () => {
it("Should implement memoized fibonacci", () => {
assert.equal(fibonacci(6), 8);
assert.equal(fibonacci(10), 55);
});
});분석:
피보나치 시리즈는 중복 지수 호출을 자체적으로 수행하기 때문에 메모리라는 전략의 혜택을 크게 누릴 수 있습니다. 다시 말해, 함수를 호출 할 때 모든 입력 및 출력의 캐시를 유지하면 호출 수가 liner 시간으로 줄어 듭니다. 물론 이것은 추가 메모리를 사용했음을 의미합니다. 코드에서 우리는 함수 자체 내에서 memoization 기법을 구현하거나, 어떤 함수를 memoization으로 decoration하는 고차 유틸리티 함수로 추상화 할 수 있습니다.
코드:
const fibonacci = (element, cache = []) => {
if (cache[element]) return cache[element];
else {
if (element < 3) return 1;
else
cache[element] =
fibonacci(element - 1, cache) + fibonacci(element - 2, cache);
}
return cache[element];
};
const _memoize = fn => {
const cache = {};
return (...args) => {
if (cache[args]) return cache[args];
const output = fn.apply(this, args);
cache[args] = output;
return output;
};
};
const _fibonacci = element =>
element < 2
? element
: _memoized_fibonacci(element - 1) + _memoized_fibonacci(element - 2);
const _memoized_fibonacci = _memoize(_fibonacci);
mocha.setup("bdd");
const { assert } = chai;
describe("Memoized Fibonacci", () => {
it("Should implement memoized fibonacci", () => {
assert.equal(fibonacci(6), 8);
assert.equal(fibonacci(10), 55);
assert.equal(_memoized_fibonacci(10), 55);
});
});
mocha.run();주어진 step 수만큼 해시와 공백을 사용하여 "계단"을 인쇄합니다.
describe("Steps", () => {
it("Should print steps", () => {
assert.equal(steps(3), "# \n## \n###\n");
assert.equal(_steps(3), "# \n## \n###\n");
});
});
분석:
핵심 키는 단계가 아래로 내려갈 때 '해시'의 증가 와 '공간' 감소 의 수를 인식하는 것입니다. 우리가n 단계를 가지고 있다면, 전체 차원은n xn입니다. 이는 시간과 공간 모두에서 런타임 복잡성이 quadratic을 의미합니다.
이 해결 방법을 사용하여 재귀 접근도 가능합니다. 필요한 임시 변수 대신 추가적인 파라미터를 전달해야합니다.
코드:
const steps = number => {
let stairs = "";
for (let row = 0; row < number; row++) {
let stair = "";
for (let column = 0; column < number; column++)
stair += column <= row ? "#" : " ";
stairs += stair + "\n";
}
return stairs;
};
const _steps = (number, row = 0, stair = "", stairs = "") => {
if (row === number) return stairs;
if (stair.length === number)
return _steps(number, row + 1, "", stairs + stair + "\n");
return _steps(number, row, stair + (stair.length <= row ? "#" : " "), stairs);
};
mocha.setup("bdd");
const { assert } = chai;
describe("Staircase", () => {
it("Should print steps", () => {
assert.equal(steps(3), "# \n## \n###\n");
assert.equal(_steps(3), "# \n## \n###\n");
});
});
mocha.run();주어진 수의 레벨에 대해 해시와 공백을 사용하여 피라미드를 인쇄합니다.
describe("Pyramid", () => {
it("Should print pyramid", () => {
assert.equal(pyramid(3), " # \n ### \n#####\n");
assert.equal(_pyramid(3), " # \n ### \n#####\n");
});
});분석:
핵심 키는n 단계 (높이)를 가진 피라미드의 너비가2 * n-1이라는 것을 인식하는 것입니다. 그런 다음 레벨을 내려 가면서 중심에서 바깥쪽으로 시작하여 해시 수와 공간 수 감소의 문제입니다. 이 알고리즘은2 * n-1 크기의n 피라미드를 반복적으로 구축하기 때문에 시간과 공간 모두에 대해 'quadratic'런타임 복잡성을 갖는다.
이 해결 방법을 사용하여 재귀 접근도 가능합니다. 필요한 임시 변수 대신 추가적으로 매개 변수를 전달해야합니다.
코드:
const pyramid = number => {
let levels = "";
const midpoint = Math.floor((2 * number - 1) / 2);
for (let row = 0; row < number; row++) {
let level = "";
for (let column = 0; column < 2 * number - 1; column++)
level += midpoint - row <= column && column <= midpoint + row ? "#" : " ";
levels += level + "\n";
}
return levels;
};
const _pyramid = (number, row = 0, level = "", levels = "") => {
if (number === row) return levels;
if (2 * number - 1 === level.length)
return _pyramid(number, row + 1, "", levels + level + "\n");
const midpoint = Math.floor((2 * number - 1) / 2);
return _pyramid(
number,
row,
level +
(midpoint - row <= level.length && level.length <= midpoint + row
? "#"
: " "),
levels
);
};
mocha.setup("bdd");
const { assert } = chai;
describe("Pyramid", () => {
it("Should print pyramid", () => {
assert.equal(pyramid(3), " # \n ### \n#####\n");
assert.equal(_pyramid(3), " # \n ### \n#####\n");
});
});
mocha.run();엘리먼트가 나선형 순서로 지정된 크기의 정사각 행렬을 만듧니다.
describe("Matrix Spiral", () => {
it("Should implement matrix spiral", () => {
assert.deepEqual(spiral(3), [[1, 2, 3], [8, 9, 4], [7, 6, 5]]);
});
});분석:
매우 어려운 문제이지만, 트릭은 시작과 끝 모두에서 현재 행과 현재 열을 가리키는 임시 변수를 만드는 것입니다. 이런 식으로 시작 행과 시작 열을 반복적으로 증가시키고 행렬의 중심을 향하여 나선형으로 끝나는 행과 끝 열을 감소시킬 수 있습니다. 이 알고리즘은 주어진 크기의 정사각 행렬을 반복적으로 생성하기 때문에 런타임 복잡도는 시간과 공간 모두에 대해 quadratic적입니다.
코드:
const spiral = number => {
let counter = 1;
let startRow = 0,
endRow = number - 1;
let startColumn = 0,
endColumn = number - 1;
const matrix = [];
for (let i = 0; i < number; i++) matrix.push([]);
while (startColumn <= endColumn && startRow <= endRow) {
// Start Row
for (let i = startColumn; i <= endColumn; i++) {
matrix[startRow][i] = counter;
counter++;
}
startRow++;
// End Column
for (let i = startRow; i <= endRow; i++) {
matrix[i][endColumn] = counter;
counter++;
}
endColumn--;
// End Row
for (let i = endColumn; i >= startColumn; i--) {
matrix[endRow][i] = counter;
counter++;
}
endRow--;
// Start Column
for (let i = endRow; i >= startRow; i--) {
matrix[i][startColumn] = counter;
counter++;
}
startColumn++;
}
return matrix;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Matrix Spiral", () => {
it("Should implement matrix spiral", () => {
assert.deepEqual(spiral(3), [[1, 2, 3], [8, 9, 4], [7, 6, 5]]);
});
});
mocha.run();데이터 구조는 알고르짐의 "빌딩 블록" 이므로 가장 인기 있는 것을 찾는 것이 좋습니다.
다시 한 번 높은 수준의 빠른 분석을 위해 다음을 확인하세요.
https://medium.com/siliconwat/data-structures-in-javascript-1b9aed0ea17c
두 개의 큐가 입력으로 주어지면 함께 "weaving"하여 새로운 대기열을 만듧니다.
describe("Weaving with Queues", () => {
it("Should weave two queues together", () => {
const one = new Queue();
one.enqueue(1);
one.enqueue(2);
one.enqueue(3);
const two = new Queue();
two.enqueue("one");
two.enqueue("two");
two.enqueue("three");
const result = weave(one, two);
assert.equal(result.dequeue(), 1);
assert.equal(result.dequeue(), "one");
assert.equal(result.dequeue(), 2);
assert.equal(result.dequeue(), "two");
assert.equal(result.dequeue(), 3);
assert.equal(result.dequeue(), "three");
assert.equal(result.dequeue(), undefined);
});분석:
최소한 Queue 클래스에는 enqueue, dequeue 및 peek 메소드가 있어야합니다. 그런 다음 while loop를 사용하여 존재 여부를 확인할 수 있으며, 존재하는 경우 인 경우 큐에서 빼낸 다음 새 큐로 큐에 넣을 수 있습니다. 이 알고리즘은 두 개의 서로 다른 컬렉션을 반복하여 저장해야하므로 시간과 공간 모두에 대해 O (n + m)을 갖습니다.
코드:
class Queue {
constructor() {
this.data = [];
}
enqueue(record) {
this.data.unshift(record);
}
dequeue() {
return this.data.pop();
}
peek() {
return this.data[this.data.length - 1];
}
}
const weave = (queueOne, queueTwo) => {
const queueCombined = new Queue();
while (queueOne.peek() || queueTwo.peek()) {
if (queueOne.peek()) queueCombined.enqueue(queueOne.dequeue());
if (queueTwo.peek()) queueCombined.enqueue(queueTwo.dequeue());
}
return queueCombined;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Weaving with Queues", () => {
it("Should weave two queues together", () => {
const one = new Queue();
one.enqueue(1);
one.enqueue(2);
one.enqueue(3);
const two = new Queue();
two.enqueue("one");
two.enqueue("two");
two.enqueue("three");
const result = weave(one, two);
assert.equal(result.dequeue(), 1);
assert.equal(result.dequeue(), "one");
assert.equal(result.dequeue(), 2);
assert.equal(result.dequeue(), "two");
assert.equal(result.dequeue(), 3);
assert.equal(result.dequeue(), "three");
assert.equal(result.dequeue(), undefined);
});
});
mocha.run();두 개의 스택을 사용하여 큐 클래스를 구현하세요.
describe("Queue from Stacks", () => {
it("Should implement queue using two stacks", () => {
const queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
assert.equal(queue.peek(), 1);
assert.equal(queue.dequeue(), 1);
assert.equal(queue.dequeue(), 2);
assert.equal(queue.dequeue(), 3);
assert.equal(queue.dequeue(), undefined);
});
});
분석:
두 개의 스택을 초기화하는 클래스 생성자로 시작할 수 있습니다. 마지막으로 삽입 된 레코드는 스택에서 제거 된 첫 번째 레코드이므로 큐의 동작을 모방하기 위해 마지막 레코드로 "dequeue"또는 "peek"로 loof해야합니다. 따라서 삽입 된 첫 번째 레코드는 첫 번째 레코드가 제거됩니다. 우리는 두 번째 스택을 사용하여 첫 번째 스택의 모든 항목을 끝에 도달 할 때까지 임시로 보유함으로써 이를 수행 할 수 있습니다. "peeking"또는 "dequeuing"후에는 모든 것을 첫 번째 스택으로 다시 옮깁니다. 레코드를“큐에 넣기”위해 간단히 첫 번째 스택으로 밀어 넣을 수 있습니다. 우리는 두 개의 스택을 사용하고 두 번 반복해야하지만이 알고리즘은 여전히 시간과 공간에서 점진적으로 linear입니다.
코드:
class Stack {
constructor() {
this.data = [];
}
push(record) {
this.data.push(record);
}
pop() {
return this.data.pop();
}
peek() {
return this.data[this.data.length - 1];
}
}
class Queue {
constructor() {
this.first = new Stack();
this.second = new Stack();
}
enqueue(record) {
this.first.push(record);
}
dequeue() {
while (this.first.peek()) {
this.second.push(this.first.pop());
}
const record = this.second.pop();
while (this.second.peek()) {
this.first.push(this.second.pop());
}
return record;
}
peek() {
while (this.first.peek()) {
this.second.push(this.first.pop());
}
const record = this.second.peek();
while (this.second.peek()) {
this.first.push(this.second.pop());
}
return record;
}
}
mocha.setup("bdd");
const { assert } = chai;
describe("Queue from Stacks", () => {
it("Should implement queue using two stacks", () => {
const queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
assert.equal(queue.peek(), 1);
assert.equal(queue.dequeue(), 1);
assert.equal(queue.dequeue(), 2);
assert.equal(queue.dequeue(), 3);
assert.equal(queue.dequeue(), undefined);
});
});
mocha.run();단일 링크드 리스트에는 일반적으로 다음 함수가 있습니다.
describe("Linked List", () => {
it("Should implement insertHead", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.head.data, 1);
}); it("Should implement size", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.size(), 1);
}); it("Should implement getHead", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.getHead().data, 1);
}); it("Should implement getTail", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.getTail().data, 1);
}); it("Should implement clear", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.clear();
assert.equal(chain.size(), 0);
}); it("Should implement removeHead", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.removeHead();
assert.equal(chain.size(), 0);
}); it("Should implement removeTail", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.removeTail();
assert.equal(chain.size(), 0);
}); it("Should implement insertTail", () => {
const chain = new LinkedList();
chain.insertTail(1);
assert.equal(chain.getTail().data, 1);
}); it("Should implement getAt", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.getAt(0).data, 1);
}); it("Should implement removeAt", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.removeAt(0);
assert.equal(chain.size(), 0);
}); it("Should implement insertAt", () => {
const chain = new LinkedList();
chain.insertAt(0, 1);
assert.equal(chain.getAt(0).data, 1);
}); it("Should implement forEach", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.forEach((node, index) => (node.data = node.data + index));
assert.equal(chain.getTail().data, 2);
}); it("Should implement iterator", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
for (let node of chain) node.data = node.data + 1;
assert.equal(chain.getTail().data, 2);
});
});코드:
class Node {
constructor(data, next = null) {
this.data = data;
this.next = next;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertHead(data) {
this.head = new Node(data, this.head);
}
size() {
let counter = 0;
let node = this.head;
while (node) {
counter++;
node = node.next;
}
return counter;
}
getHead() {
return this.head;
}
getTail() {
if (!this.head) return null;
let node = this.head;
while (node) {
if (!node.next) return node;
node = node.next;
}
}
clear() {
this.head = null;
}
removeHead() {
if (!this.head) return;
this.head = this.head.next;
}
removeTail() {
if (!this.head) return;
if (!this.head.next) {
this.head = null;
return;
}
let previous = this.head;
let node = this.head.next;
while (node.next) {
previous = node;
node = node.next;
}
previous.next = null;
}
insertTail(data) {
const last = this.getTail();
if (last) last.next = new Node(data);
else this.head = new Node(data);
}
getAt(index) {
let counter = 0;
let node = this.head;
while (node) {
if (counter === index) return node;
counter++;
node = node.next;
}
return null;
}
removeAt(index) {
if (!this.head) return;
if (index === 0) {
this.head = this.head.next;
return;
}
const previous = this.getAt(index - 1);
if (!previous || !previous.next) return;
previous.next = previous.next.next;
}
insertAt(index, data) {
if (!this.head) {
this.head = new Node(data);
return;
}
if (index === 0) {
this.head = new Node(data, this.head);
return;
}
const previous = this.getAt(index - 1) || this.getLast();
const node = new Node(data, previous.next);
previous.next = node;
}
forEach(fn) {
let node = this.head;
let index = 0;
while (node) {
fn(node, index);
node = node.next;
index++;
}
}
*[Symbol.iterator]() {
let node = this.head;
while (node) {
yield node;
node = node.next;
}
}
}
mocha.setup("bdd");
const { assert } = chai;
describe("Linked List", () => {
it("Should implement insertHead", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.head.data, 1);
});
it("Should implement size", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.size(), 1);
});
it("Should implement getHead", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.getHead().data, 1);
});
it("Should implement getTail", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.getTail().data, 1);
});
it("Should implement clear", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.clear();
assert.equal(chain.size(), 0);
});
it("Should implement removeHead", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.removeHead();
assert.equal(chain.size(), 0);
});
it("Should implement removeTail", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.removeTail();
assert.equal(chain.size(), 0);
});
it("Should implement insertTail", () => {
const chain = new LinkedList();
chain.insertTail(1);
assert.equal(chain.getTail().data, 1);
});
it("Should implement getAt", () => {
const chain = new LinkedList();
chain.insertHead(1);
assert.equal(chain.getAt(0).data, 1);
});
it("Should implement removeAt", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.removeAt(0);
assert.equal(chain.size(), 0);
});
it("Should implement insertAt", () => {
const chain = new LinkedList();
chain.insertAt(0, 1);
assert.equal(chain.getAt(0).data, 1);
});
it("Should implement forEach", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.forEach((node, index) => (node.data = node.data + index));
assert.equal(chain.getTail().data, 2);
});
it("Should implement iterator", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
for (let node of chain) node.data = node.data + 1;
assert.equal(chain.getTail().data, 2);
});
});
mocha.run();도전 #1: Midpoint
도전 # 1 : 중간 점 카운터를 유지하지 않고 연결된 리스트의 중간 값을 반환하십시오.
describe("Midpoint of Linked List", () => {
it("Should return midpoint of linked list", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.insertHead(3);
chain.insertHead(4);
chain.insertHead(5);
assert.equal(midpoint(chain).data, 3);
});
});
분석:
이 트릭은 리스트를 2배 순환하는 것입니다. 그 중 하나는 2 배 빠릅니다. 더 빠른 것이 끝에 도달하면, 하나는 중간에 멈 춥니 다! 이 알고리즘에는 linear시간과 constant 공간이 있습니다.
코드:
class Node {
constructor(data, next = null) {
this.data = data;
this.next = next;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertHead(data) {
this.head = new Node(data, this.head);
}
}
function midpoint(list) {
let moveByOne = list.head;
let moveByTwo = list.head;
while (moveByTwo.next && moveByTwo.next.next) {
moveByOne = moveByOne.next;
moveByTwo = moveByTwo.next.next;
}
return moveByOne;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Midpoint of Linked List", () => {
it("Should return midpoint of linked list", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.insertHead(3);
chain.insertHead(4);
chain.insertHead(5);
assert.equal(midpoint(chain).data, 3);
});
});
mocha.run();Challenge #2: 환형
노드 참조를 유지하지 않고 연결된 목록이 환형인지 확인하십시오.
describe("Circular Linked List", () => {
it("Should check for circular linked list", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.insertHead(3);
chain.head.next.next.next = chain.head;
assert.equal(circular(chain), true);
});
});
분석:
많은 링크드 리스트의 함수는 명확한 끝 노드를 갖는 것으로 가정합니다. 따라서 원형이 아닌지 확인하는 것이 중요합니다. 다시 한 번, 리스트을 두 번 탐색하는 것이 중요하며 그 중 하나가 두 배 더 빠릅니다. 리스트가 원형이면 결국 더 빠른 리스트가 더 빨리 돌아가고 느린 리스트와 일치합니다. 여기서 루프를 종료하고 true를 반환 할 수 있습니다. 그렇지 않으면 끝에 도달하고 거짓을 반환 할 수 있습니다. 이 알고리즘에는 linear 시간과 constant 공간이 있습니다.
코드
class Node {
constructor(data, next = null) {
this.data = data;
this.next = next;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertHead(data) {
this.head = new Node(data, this.head);
}
}
function circular(list) {
let moveByOne = list.head;
let moveByTwo = list.head;
while (moveByTwo.next && moveByTwo.next.next) {
moveByOne = moveByOne.next;
moveByTwo = moveByTwo.next.next;
if (moveByTwo === moveByOne) return true;
}
return false;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Circular Linked List", () => {
it("Should check for circular linked list", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.insertHead(3);
chain.head.next.next.next = chain.head;
assert.equal(circular(chain), true);
});
});
mocha.run();Challenge #3: 끝부분으로 부터
카운터를 유지하지 않으면 서 주어진 'step'에있는 링크드리스트에서 value를 끝부분에서 부터 먼 것을 반환하십시오.
describe("From Tail of Linked List", () => {
it("Should step from tail of linked list", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.insertHead(3);
chain.insertHead(4);
chain.insertHead(5);
assert.equal(fromTail(chain, 2).data, 3);
});
});
분석:
The trick is similar to the previous in that we traverse the list two times. In this case, however, the “faster” one begins ahead of the “slower” one, at the given step away. Then, we walk them both down the list at the same pace until the faster one reaches the end. At that point, the slower one is precisely at the right step away from the end.
This algorithm also has linear time and constant space.
이 알고리즘에서의 트릭은 리스트를 두 번 탐색한다는 점에서 이전과 비슷합니다. 그러나이 경우 "빠른" 리스트는 지정된 step에서 "느린" 리스트보다 먼저 시작합니다. 그런 다음 빠른 속도가 끝날 때까지 같은 속도로 리스트를 따라 내려갑니다. 이 시점에서 느린 쪽은 끝에서 정확히 오른쪽 단계에 있습니다. 이 알고리즘에는 linear 시간과 constant 공간이 있습니다.
코드:
class Node {
constructor(data, next = null) {
this.data = data;
this.next = next;
}
}
class LinkedList {
constructor() {
this.head = null;
}
insertHead(data) {
this.head = new Node(data, this.head);
}
}
function fromTail(list, step) {
let moveByOne = list.head;
let aheadByStep = list.head;
while (step > 0) {
aheadByStep = aheadByStep.next;
step--;
}
while (aheadByStep.next) {
moveByOne = moveByOne.next;
aheadByStep = aheadByStep.next;
}
return moveByOne;
}
mocha.setup("bdd");
const { assert } = chai;
describe("From Tail of Linked List", () => {
it("Should step from tail of linked list", () => {
const chain = new LinkedList();
chain.insertHead(1);
chain.insertHead(2);
chain.insertHead(3);
chain.insertHead(4);
chain.insertHead(5);
assert.equal(fromTail(chain, 2).data, 3);
});
});
mocha.run();트리는 아래와 같은 함수로 구성되어 있습니다.
describe("Trees", () => {
it("Should add and remove nodes", () => {
const root = new Node(1);
root.add(2);
assert.equal(root.data, 1);
assert.equal(root.children[0].data, 2);
root.remove(2);
assert.equal(root.children.length, 0);
}); it("Should traverse by breadth", () => {
const tree = new Tree();
tree.root = new Node(1);
tree.root.add(2);
tree.root.add(3);
tree.root.children[0].add(4); const numbers = [];
tree.traverseBF(node => numbers.push(node.data));
assert.deepEqual(numbers, [1, 2, 3, 4]);
}); it("Should traverse by depth", () => {
const tree = new Tree();
tree.root = new Node(1);
tree.root.add(2);
tree.root.add(3);
tree.root.children[0].add(4); const numbers = [];
tree.traverseDF(node => numbers.push(node.data));
assert.deepEqual(numbers, [1, 2, 4, 3]);
});
});Challenge #1: Tree Widths
주어진 트리에 대해, 각 레벨의 width를 반환하세요.
describe("Width of Tree Levels", () => {
it("Should return width of each tree level", () => {
const root = new Node(1);
root.add(2);
root.add(3);
root.children[1].add(4); assert.deepEqual(treeWidths(root), [1, 2, 1]);
});
});
Analysis:
stack 또는 queue를 사용하여 트리를 depth first 또는 breadth first 로 트래버스하여 모든 slice 및 levels 를 각각 반복 할 수 있습니다. 우리는 각 레벨에서 모든 노드를 카운트 하고 싶기 때문에 queue의 도움을 받아 먼저 width으로 트리를 통과해야합니다. 여기서의 트릭은 현재 레벨의 끝에 도달했다는 것을 알려주기 위해 특별한 'marker'를 큐에 넣는 것이므로 다음 레벨의 카운터를 재설정 할 수 있습니다.
이 방법은 시간과 공간의 복잡성이 linear입니다. 우리의 '카운터'는 배열이지만 크기는 linear보다 클 수 없습니다.
Code:
class Node {
constructor(data) {
this.data = data;
this.children = [];
}
add(data) {
this.children.push(new Node(data));
}
}
function treeWidths(root) {
const queue = [root, "reset"];
const counters = [0];
while (queue.length > 1) {
const node = queue.shift();
if (node === "reset") {
counters.push(0);
queue.push("reset");
} else {
queue.push(...node.children);
counters[counters.length - 1]++;
}
}
return counters;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Width of Tree Levels", () => {
it("Should return width of each tree level", () => {
const root = new Node(1);
root.add(2);
root.add(3);
root.children[1].add(4);
assert.deepEqual(treeWidths(root), [1, 2, 1]);
});
});
mocha.run();Challenge #2: Tree Height
주어진 트리에 대해 height(최대 레벨 수)를 반환합니다.
describe("Height of Tree", () => {
it("Should return max number of levels", () => {
const root = new Node(1);
root.add(2);
root.add(3);
root.children[1].add(4); assert.deepEqual(treeHeight(root), 2);
});
});분석:
We can simply reuse our logic from the first challenge. In this case, however, we increment our counter whenever we encounter “reset” instead. The logic is nearly identical, so this algorithm also has a linear time and space complexity. Here, our counter is just an integer, which makes its size even more negligible.
우리는 단순히 첫 번째 challenge에서의 로직을 재사용 할 수 있습니다. 그러나이 경우 대신 "재설정"이 발생할 때마다 카운터를 증가시킵니다. 로직은 거의 동일하므로이 알고리즘에는 linear 시간 및 공간 복잡성이 있습니다. 여기서 '카운터'는 정수일 뿐이므로 크기를 훨씬 무시할 수 있습니다.
코드:
class Node {
constructor(data) {
this.data = data;
this.children = [];
}
add(data) {
this.children.push(new Node(data));
}
}
function treeHeight(root) {
const queue = [root, "reset"];
let counter = 0;
while (queue.length > 1) {
const node = queue.shift();
if (node === "reset") {
counter++;
queue.push("reset");
} else {
queue.push(...node.children);
}
}
return counter;
}
function _treeHeight(root) {
const stack = [root];
let counter = 0;
while (stack.length > 0) {
const node = stack.shift();
counter++;
stack.unshift(...node.children);
}
return counter;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Height of Tree", () => {
it("Should return max number of levels", () => {
const root = new Node(1);
root.add(2);
root.add(3);
root.children[1].add(4);
assert.deepEqual(treeHeight(root), 2);
});
});
mocha.run();다시 돌아가서 확인하세요
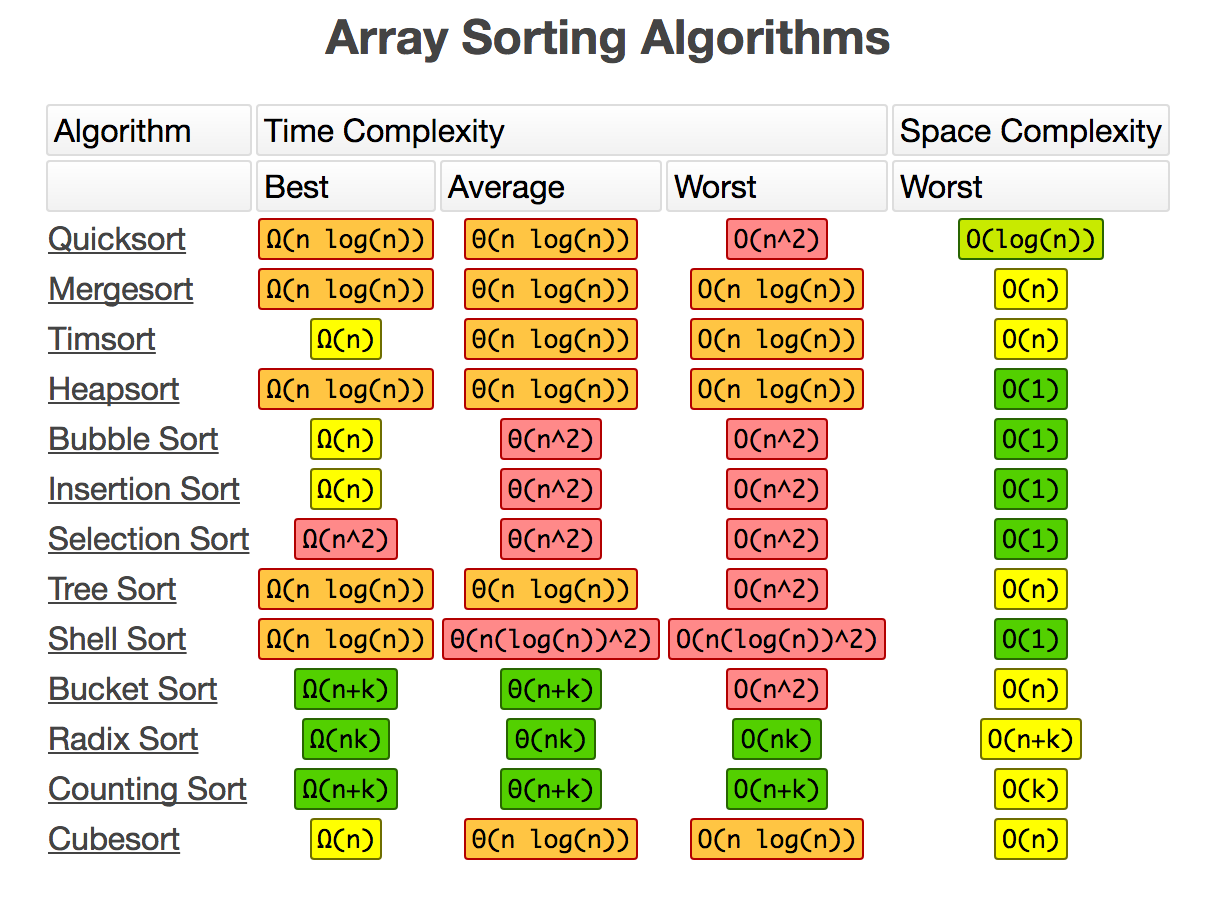
데이터 수집을 정렬하는 데 사용할 수있는 많은 알고리즘이 있습니다. 고맙게도 면접관은 우리가 기본과 첫 번째 원칙을 이해하기를 기대합니다. 예를 들어, 최상의 알고리즘은 constant 공간에서 linear시간을 달성 할 수 있습니다. 이 정신에서 우리는 어려움과 효율성을 높이기 위해 가장 인기있는 것들을 검토 할 것입니다.
이 알고리즘은 이해하기가 가장 쉽지만 가장 비효율적입니다. 모든 항목을 다른 모든 항목과 비교하여 더 큰 항목이 맨 위로 "버블 링"될 때까지 순서를 스와핑합니다. 이 알고리즘에는 quadratic 시간과 constant 공간이 필요합니다.
const bubbleSort = array => {
let swapped;
do {
swapped = false;
array.forEach((number, index) => {
if (number > array[index + 1]) {
[array[index], array[index + 1]] = [array[index + 1], array[index]];
swapped = true;
}
});
} while (swapped);
return array;
};
function _bubbleSort(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
const less = array[j + 1];
array[j + 1] = array[j];
array[j] = less;
}
}
}
return array;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Bubble Sort", () => {
it("Should implement bubble sort", () => {
assert.deepEqual(bubbleSort([5, 4, 3, 2, 1]), [1, 2, 3, 4, 5]);
assert.deepEqual(bubbleSort([5, 3, 1, 2, 4]), [1, 2, 3, 4, 5]);
assert.deepEqual(_bubbleSort([5, 4, 3, 2, 1]), [1, 2, 3, 4, 5]);
assert.deepEqual(_bubbleSort([5, 3, 1, 2, 4]), [1, 2, 3, 4, 5]);
});
});
mocha.run();버블 정렬과 마찬가지로 모든 항목은 다른 모든 항목과 비교됩니다. 교환하는 대신 올바른 순서로 "접합"됩니다. 실제로 반복되는 항목의 원래 순서를 유지합니다. 이 "탐욕"알고리즘에는 quadratic 시간과 constant 공간이 필요합니다.
const insertionSort = array => {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < i; j++) {
if (array[i] < array[j]) array.splice(j, 0, array.splice(i, 1)[0]);
}
}
return array;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Insertion Sort", () => {
it("Should implement insertion sort", () => {
assert.deepEqual(insertionSort([4, 3, 3, 2, 1]), [1, 2, 3, 3, 4]);
assert.deepEqual(insertionSort([4, 3, 1, 2, 3]), [1, 2, 3, 3, 4]);
});
});
mocha.run();loop가 콜렉션을 반복 할 때이 알고리즘은 가장 낮은 값으로 인덱스를 찾아서 "선택"하고 시작 인덱스와 적절한 위치에 교환합니다. 이 알고리즘에는 quadratic 시간과 constant 공간도 필요합니다.
function selectionSort(array) {
for (let i = 0; i < array.length; i++) {
let indexOfMin = i;
for (let j = i + 1; j < array.length; j++)
if (array[j] < array[indexOfMin]) indexOfMin = j;
if (indexOfMin !== i) {
let less = array[indexOfMin];
array[indexOfMin] = array[i];
array[i] = less;
}
}
return array;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Selection Sort", () => {
it("Should sort an array", () => {
assert.deepEqual(selectionSort([5, 4, 3, 2, 1]), [1, 2, 3, 4, 5]);
});
});
mocha.run();This algorithm recursively selects an element as the pivot and iteratively pushes all the smaller elements to the left and all the larger elements to the right until all is sorted. This algorithm requires quadratic time and logarithmic space such that in practice is often the fastest. As such, most programming languages natively implement this algorithm for sorting.
이 알고리즘은 요소를 피벗으로 재귀 적으로 선택하고 모든 정렬 될 때까지 모든 작은 요소를 왼쪽으로, 큰 요소를 모두 오른쪽으로 반복해서 푸시합니다. 이 알고리즘은 실제로는 가장 빠른 이되도록 quadratic 시간과 logarithmic 공간이 필요합니다. 따라서 대부분의 프로그래밍 언어는 기본적으로 정렬을 위해이 알고리즘을 구현합니다.
const quickSort = array => {
if (array.length < 2) return array;
const pivot = array[array.length - 1];
const left = [],
right = [];
for (let i = 0; i < array.length - 1; i++) {
if (array[i] < pivot) left.push(array[i]);
else right.push(array[i]);
}
return [...quickSort(left), pivot, ...quickSort(right)];
};
mocha.setup("bdd");
const { assert } = chai;
describe("Quick Sort", () => {
it("Should implement quick sort", () => {
assert.deepEqual(quickSort([5, 4, 3, 2, 1]), [1, 2, 3, 4, 5]);
assert.deepEqual(quickSort([5, 3, 1, 2, 4]), [1, 2, 3, 4, 5]);
});
});
mocha.run();가장 효율적인 방법 중 하나이지만이 알고리즘은 이해하기 어려울 수 있습니다. 컬렉션을 단일 단위로 분할한 다음 반복적 인 부분을 올바른 순서로 다시 결합하는 반복적 인 부분이 필요합니다. 이 알고리즘은 linear 시간과 linear 공간을 사용합니다.
const mergeSort = array => {
if (array.length < 2) return array;
const middle = Math.floor(array.length / 2);
const left = array.slice(0, middle),
right = array.slice(middle, array.length);
return merge(mergeSort(left), mergeSort(right));
};
const merge = (left, right) => {
const result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) result.push(left.shift());
else result.push(right.shift());
}
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
return result;
};
function _mergeSort(array) {
if (array.length === 1) return array;
const center = Math.floor(array.length / 2);
const left = array.slice(0, center);
const right = array.slice(center);
return _merge(_mergeSort(left), _mergeSort(right));
}
function _merge(left, right) {
const results = [];
while (left.length && right.length) {
if (left[0] < right[0]) results.push(left.shift());
else results.push(right.shift());
}
return [...results, ...left, ...right];
}
mocha.setup("bdd");
const { assert } = chai;
describe("Merge Sort", () => {
it("Should implement merge sort", () => {
assert.deepEqual(mergeSort([5, 4, 3, 2, 1]), [1, 2, 3, 4, 5]);
assert.deepEqual(mergeSort([5, 3, 1, 2, 4]), [1, 2, 3, 4, 5]);
assert.deepEqual(_mergeSort([5, 4, 3, 2, 1]), [1, 2, 3, 4, 5]);
assert.deepEqual(_mergeSort([5, 3, 1, 2, 4]), [1, 2, 3, 4, 5]);
});
});
mocha.run();어떻게 든 최대 값을 알면이 알고리즘을 사용하여 linear 시간과 공간으로 모음을 정렬 할 수 있습니다! 최대 값을 사용하면 각 인덱스 값의 발생을 계산하기 위해 해당 크기의 배열을 만들 수 있습니다. 그런 다음 0이 아닌 모든 인덱스를 결과 배열로 추출하면됩니다. 배열의 상수 시간 조회를 활용하여이 해시 유사 알고리즘이 가장 성능이 우수합니다.
const countingSort = (array, max) => {
const counts = new Array(max + 1);
counts.fill(0);
array.forEach(value => counts[value]++);
const result = [];
let resultIndex = 0;
counts.forEach((count, index) => {
for (let i = 0; i < count; i++) {
result[resultIndex] = index;
resultIndex++;
}
});
return result;
};
mocha.setup("bdd");
const { assert } = chai;
describe("Counting Sort", () => {
it("Should implement counting sort", () => {
assert.deepEqual(countingSort([4, 3, 2, 1, 0], 4), [0, 1, 2, 3, 4]);
assert.deepEqual(countingSort([4, 3, 1, 2, 3], 4), [1, 2, 3, 3, 4]);
});
});
mocha.run();최악의 알고리즘은 'O (n)`시간이 걸리는 컬렉션의 모든 항목을 검색해야합니다. 어떻게 든 컬렉션이 이미 정렬되어 있다면, 반복 할 때마다 절반 만 확인하면되며, 단지 'O (log n)'시간 만 사용하면 특히 대규모 데이터 세트의 경우 성능이 크게 향상됩니다.
컬렉션이 정렬되면 중간 값에 대해 원하는 값을 반복적으로 또는 재귀 적으로 확인할 수 있으며 값이 존재할 수 없다는 것을 절반은 무시합니다. 실제로 우리의 목표는 logarithmic시간과 constant 공간에서 찾는 것입니다.
const binarySearch = (array, value) => {
const midIndex = Math.floor(array.length / 2);
const midValue = array[midIndex];
if (value === midValue) return true;
else if (array.length > 1 && value < midValue)
return binarySearch(array.splice(0, midIndex), value);
else if (array.length > 1 && value > midValue)
return binarySearch(array.splice(midIndex + 1, array.length), value);
else return false;
};
function _binarySearch(nums, target) {
// see if target appears in nums
// we think of floorIndex and ceilingIndex as "walls" around
// the possible positions of our target, so by -1 below we mean
// to start our wall "to the left" of the 0th index
// (we *don't* mean "the last index")
var floorIndex = -1;
var ceilingIndex = nums.length;
// if there isn't at least 1 index between floor and ceiling,
// we've run out of guesses and the number must not be present
while (floorIndex + 1 < ceilingIndex) {
// find the index ~halfway between the floor and ceiling
// we have to round down, to avoid getting a "half index"
var distance = ceilingIndex - floorIndex;
var halfDistance = Math.floor(distance / 2);
var guessIndex = floorIndex + halfDistance;
var guessValue = nums[guessIndex];
if (guessValue === target) {
return true;
}
if (guessValue > target) {
// target is to the left, so move ceiling to the left
ceilingIndex = guessIndex;
} else {
// target is to the right, so move floor to the right
floorIndex = guessIndex;
}
}
return false;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Binary Search", () => {
it("Should implement binary search", () => {
assert.equal(binarySearch([1, 2, 3, 4, 5], 0), false);
assert.equal(binarySearch([1, 2, 3, 4, 5, 6], 6), true);
assert.equal(_binarySearch([1, 2, 3, 4, 5], 0), false);
assert.equal(_binarySearch([1, 2, 3, 4, 5, 6], 6), true);
});
});
mocha.run();컬렉션을 정렬하는 대안은 이진 검색 트리 (BST)를 생성하는 것입니다. BST로서 검색은 이진 검색만큼 효율적입니다. 비슷한 방식으로 반복 할 때마다 원하는 값을 포함 할 수없는 절반을 버릴 수 있습니다. 실제로 컬렉션을 정렬하는 또 다른 방법은이 트리에서 깊이 우선 순회를 순서대로 수행하는 것입니다! BST 생성은 선형 시간과 공간에서 발생하지만 검색은 logarithmic시간과 constant 공간에서 발생합니다.
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
insert(data) {
if (data < this.data && this.left) this.left.insert(data);
else if (data < this.data) this.left = new Node(data);
else if (data > this.data && this.right) this.right.insert(data);
else if (data > this.data) this.right = new Node(data);
}
search(data) {
if (this.data === data) return this;
if (this.data < data && this.right) return this.right.search(data);
else if (this.data > data && this.left) return this.left.search(data);
return null;
}
}
mocha.setup("bdd");
const { assert } = chai;
describe("Binary Search Tree", () => {
it("Should insert node", () => {
const root = new Node(2);
root.insert(1);
root.insert(3);
root.insert(0);
assert.equal(root.left.left.data, 0);
});
it("Should implement search", () => {
const root = new Node(2);
root.insert(1);
root.insert(3);
root.insert(0);
assert.equal(root.search(3).data, 3);
assert.equal(root.search(4), null);
});
});
mocha.run();이진 트리가 BST인지 확인하기 위해 모든 왼쪽 자식은 루트보다 작아야하고 (가능한 최대) 모든 오른쪽 자식은 루트마다 루트 (최소한)보다 커야한다는 것을 재귀 적으로 확인할 수 있습니다. 이 솔루션에는 선형 시간과 일정한 공간이 필요합니다.
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
insert(data) {
if (data < this.data && this.left) this.left.insert(data);
else if (data < this.data) this.left = new Node(data);
else if (data > this.data && this.right) this.right.insert(data);
else if (data > this.data) this.right = new Node(data);
}
}
function validate(node, min = null, max = null) {
if (max !== null && node.data > max) return false;
if (min !== null && node.data < min) return false;
if (node.left && !validate(node.left, min, node.data)) return false;
if (node.right && !validate(node.right, node.data, max)) return false;
return true;
}
mocha.setup("bdd");
const { assert } = chai;
describe("Validate a Binary Search Tree", () => {
it("Should validate a binary search tree", () => {
const root = new Node(2);
root.insert(1);
root.insert(3);
root.insert(0);
assert.equal(validate(root), true);
});
});
mocha.run();현대 웹 개발에서 함수는 웹 경험의 핵심입니다. 데이터 구조는 기능을 입력 및 종료하고 알고리즘 은 내부 역학을 지시합니다. 데이터 구조가 확장되는 방식은 공간 복잡성으로 설명되는 반면 알고리즘이 확장되는 방식은 시간 복잡성으로 설명됩니다. 실제로 런타임 복잡도는 Big-O 표기법으로 표현되므로 엔지니어가 모든 솔루션 가능성을 비교하고 대조 할 수 있습니다. 가장 효율적인 런타임은 constant 이며 입력 크기에 의존하지 않습니다. 가장 비효율적 인 것은 지수 연산과 메모리를 요구합니다. 알고리즘과 데이터 구조를 진정으로 마스터하는 것은 linear과 systemically을 동시에 병렬로 추리 할 수 있어야합니다.
이론적으로 모든 문제에는 반복 솔루션과 재귀 솔루션이 모두 있습니다. 반복적 인 접근 방식은 맨 아래부터 시작하여 동적으로 솔루션에 도달합니다. 재귀 적 접근은 중복 하위 문제를 인식함으로써 위에서부터 시작됩니다. 일반적으로 재귀 솔루션은 구현하기가 더 표현적이고 단순하지만 반복 솔루션은 정리하기 쉽고 메모리가 덜 필요합니다. first-class 함수와 control-flow 구문으로 JavaScript는 기본적으로 두 가지 접근 방식을 모두 지원합니다. 일반적으로 성능 향상을 위해 공간 효율성을 희생하거나 메모리 사용량을 줄이려면 시간 효율성을 희생해야합니다. 적절한 균형은 상황과 환경에 따라 다릅니다. 고맙게도 대부분의 면접관들은 결과보다 미적분학에 더 관심을 가지고 있습니다.
면접관에게 깊은 인상을주기 위해 재사용 가능성과 유지 보수성을 향상시키는 아키텍처 **와 ** 디자인 패턴을 활용할 수있는 기회를 찾기 위해 자신의 시야를 넓히십시오. 고위 직책을 찾고 있다면 기본 및 기본 원칙에 대한 지식과 시스템 수준의 설계 경험이 똑같이 중요합니다. 그럼에도 불구하고, 최고의 회사는 문화적 적합성을 평가합니다. 완벽한 사람은 없기 때문에 올바른 팀이 필수적입니다. 더 중요한 것은,이 세상의 일부 것들만으로는 불가능하다는 것입니다. 종종 우리가 함께 그리고 서로를 위해 만드는 것들이 가장 만족스럽고 의미있는 것입니다.