La signature électronique

Si l’on veut garantir l’authenticité de l’émetteur d’un document, on utilise ce que l’on appelle une signature électronique. Par la suite, on appelle H la fonction de hachage. On appellera C l’action de chiffrer et D déchiffrer.

A veut envoyer un message M à B A crée un haché du document H(M) A chiffre H(M) avec sa clé privée : C(H(M)) A envoie M et C(H(M)) B récupère tout ça B crée un haché du document H(M) B utilise la clé publique de A et compare H(M) à D(C(H(M))) Alors, si c’est bien A qui a envoyé les documents, D(C(H(M))) = H(M) et B est certain de l’émetteur.

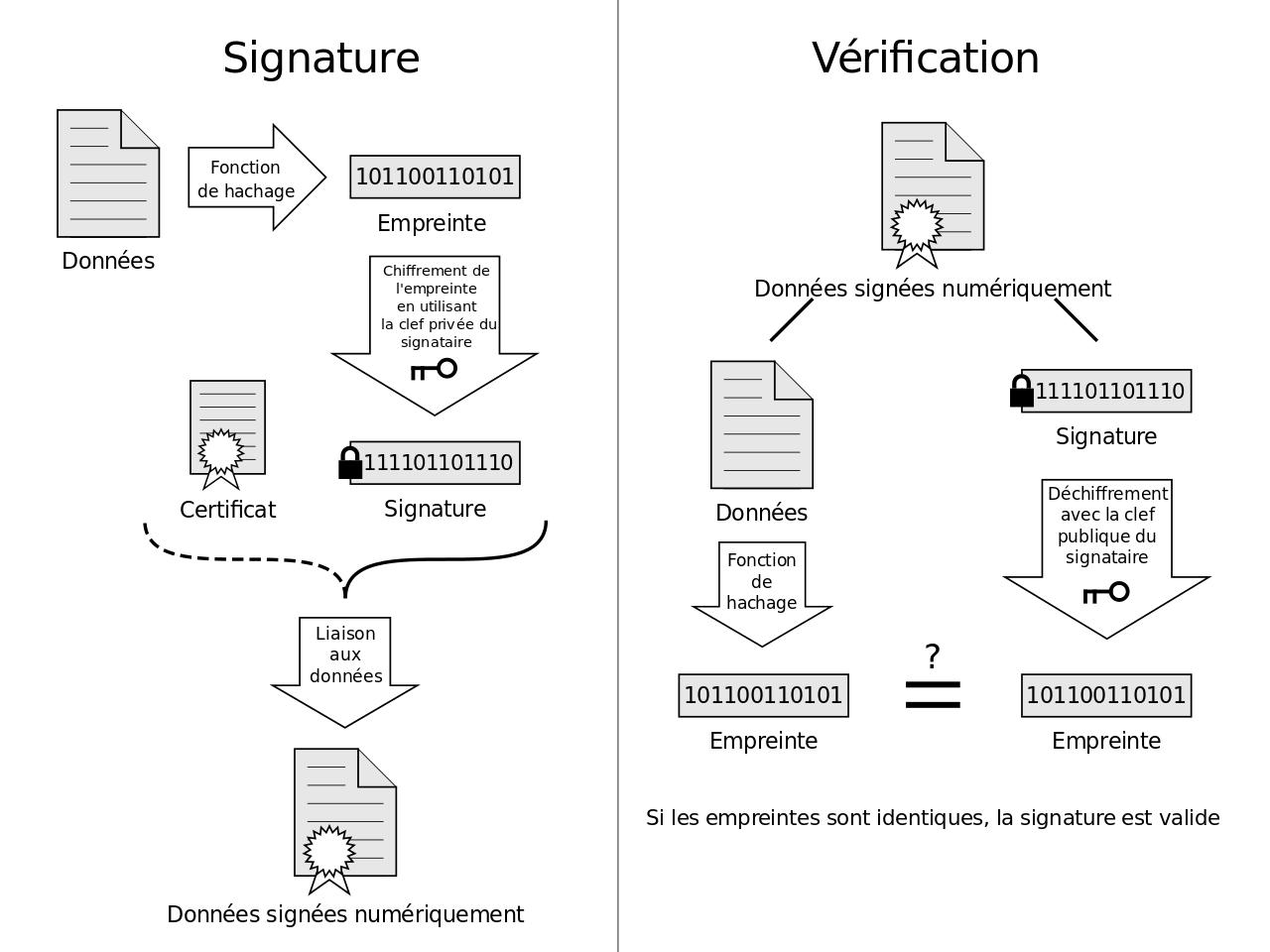
Imaginez que nous n’ayons pas utilisé de fonction de hachage, alors avec un document très gros on devrait chiffrer et déchiffrer des documents énormes, transmettre beaucoup plus de données, … Avec une fonction de hachage, on a toujours on manipule des messages de taille fixes.

Quel peut être le problème d’une collision ? Le problème, c’est que l’on peut faire des attaques très vilaines en partant d’une collision. Un exemple sera plus parlant qu’un long discours :

M crée deux documents d1 et d2 ayant le même haché (c’est une collision). M envoie le document d1 à A, qui accepte et signe le haché et envoie la signature à M.

M attache la signature de d1 à d2, et envoie le d2 à B.

B croit alors que A a signé le document d2, alors que ce n’est pas vrai (A a signé d1).

Exemple :

Cet exemple n’est pas du tout réaliste, mais c’est pour bien comprendre le principe.

Le document d1 est le suivant : "Tu me dois 10€" Le document d2 est le suivant : "Tu me dois 10000000€" Ils ont le même haché par la fonction bidon ("Tu me do").

M envoie d1 à A, qui est d’accord pour payer 10€. A signe donc le document en ajoutant sa signature S. Cela donne l’ensemble d1+S qui dit que A est d’accord sur les termes du document d1.

Mais alors, M signe alors d2 avec S et obtient d2+S avec S qui est une bonne signature de A sur d1, mais aussi sur d2 car d1 et d2 ont les mêmes hachés.

Maintenant, d’après le document d2+S que M possède, A est d’accord pour payer 10000000€, ce qui n’est évidemment pas le cas.