Elliptic curve

Introduction

Cela sert à deux acteurs d'échanger une clef de façon sécurisé ou dans les chiffrements asymétriques ou pour réaliser des signatures numériques : elle est une méthode très utilisé aujourd'hui.

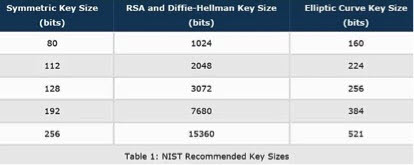
Pourquoi utiliser les courbes elliptiques dans la cryptographie? C'est une méthode qui permet le calcul de clef qui utilise peu de mémoire et de ressources CPU. Le facteur de différenciation clé entre l’ECC et RSA est la taille de la clé comparé à la force de chiffrement. Comme le montre le tableau ci-dessus, l’ECC peut fournir la même force de chiffrement qu’un système basé sur l’algorithme RSA, mais avec des clés beaucoup plus courtes. La difficulté se base sur la difficulté du calcul du logarithme discret.

La courbe elliptique

Une Courbe Elliptic est une courbe qui appartient à cet ensemble

$E = {{(x,y) | y^2 = x^3 +ax +b}}$ avec $(a,b) \in K$ avec K soit $\mathbb{R}$ ou $\mathbb{C}$ ou $\mathbb{Q}$ ou $\mathbb{Z}/p\mathbb{Z}$ et que $4a^3 + 27b^2 \neq 0$ (Dont le discriminant est différent de 0)

Voici pour des valeurs de (a,b) ce que cela donne graphiquement :

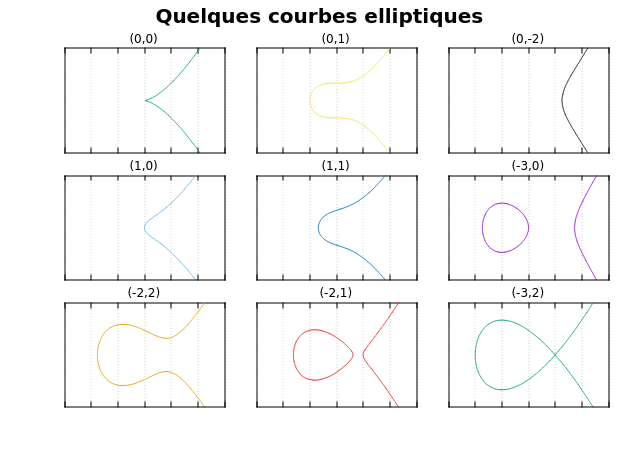
On remarque qu'il ne s'agit pas d'ellipses

On remarquera deux caractéristique géométrique de cette courbe :

• Cette courbe est symétrique par rapport à l'axe x. (Ainsi toute droite non verticale coupant deux points sur une courbe elliptique va toujours couper cette dernière en un 3ième point.)

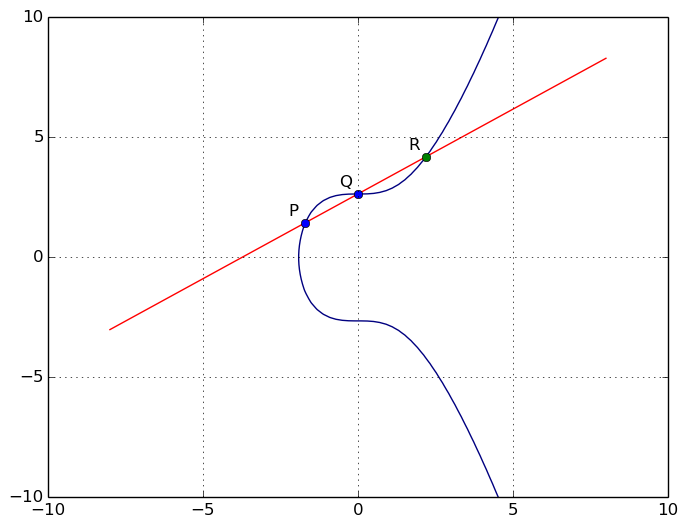
• Toute ligne non verticale et tangente à la courbe en 1 point : coupera la courbe en 1 seul et unique point

Il existe plusieurs standards de courbe elliptique : réputé sur pour une utilisation cryptographique comme la secp256r1, secp256k1. Prenons ainsi l'exemple de secp256k1 qui est défini par $y^2 = x^3 + 7$ (a=0 et b=7)

En réalité nous travaillons sur un corps fini appelé $\mathbb{Z}_p$ qui sont des entiers positifs modulo p où p est un nombre premier. Donc au final la source secp256k1 est une courbe qui est plutôt un nuage de point (qu'on appelle groupe elliptique) plutôt qu'une courbe continue. Avec $p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F = 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1$ pour secp256k1

Exemple : $y^2 = x^3 + 7$ (a=0 et b=7) avec p=17

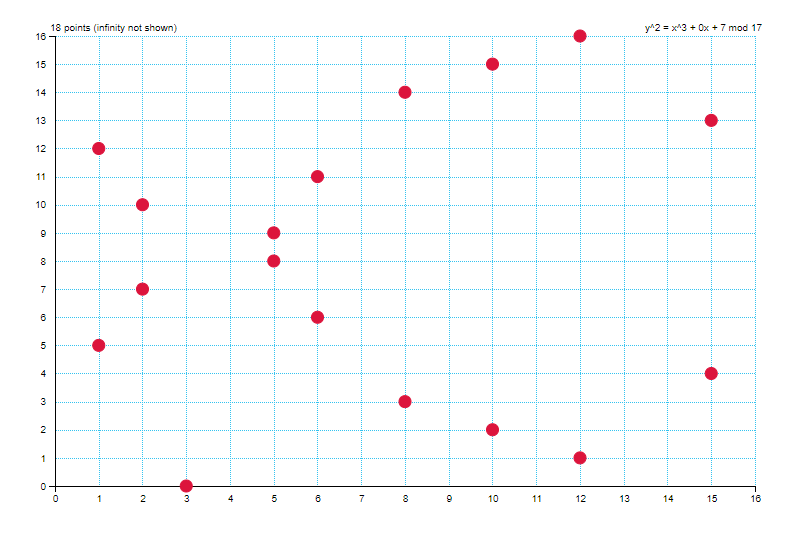
Les groupes elliptiques

Pour éviter les erreurs d'approximations en informatique nous travaillerons qu'avec des entiers. $y^2 mod(p) = (x^3 + ax + b) mod (p)$

On note : $E_p(a,b)$ l'ensemble des couples d'entiers (x,y) qui respecte l'équation ci dessus on parle de groupe elliptique.

Exemple :

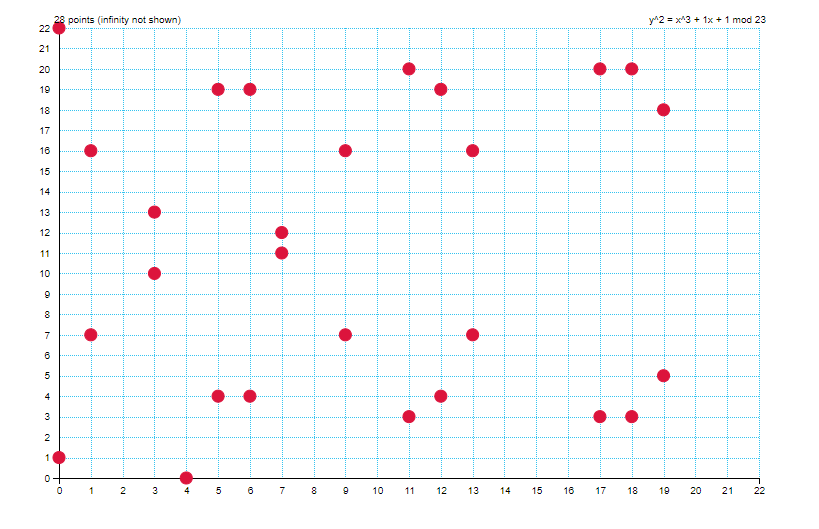
Si on prend $p=23$ et la courbe elliptique $y^2 = x^ + x + 1$

On est donc dans l'ensemble $E_{23}(1,1)$. Si nous travaillons dans $\mathbb{Z}_p$ les couples $(x,y)$ qui respecte l'équation sont les suivants : $(0,1)$ : $(6,4)$ : $(12,19)$ : $(0,22)$ : ... : (19,18) (27 solutions) comme le montre le schémas ci dessous

Clée publique, Clée privée

Soient les paramètres (A, B, P, G, n) tels que :

• La courbe C définie par : $y^2 = x^3 + Ax + B (mod P)$
• G un point de la courbe
• n le nombre entier tel que n * G = 0 (Correspond au nombre de groupes elliptiques: dans l'exemple ci dessus 28)

Pour générer une clé privée, il suffit de choisir au hasard un nombre s entre 1 et N - 1. Facile, non ? La clé publique, quand à elle, est égale au point $Q = s \times G.$

Connaissant s et G, vous savez désormais qu'il est très facile de calculer Q. En revanche, il est virtuellement impossible de retrouver s à partir de G et Q. Du moins, pas sans disposer de quelques millions d'années devant vous.