A polynomial function is defined as a linear combination of the powers of the variable (usually $x$)

• $a_i$ are the coefficients
• Each $a_ix^i$ are the terms

A quadratic function is a polynomial function of 2nd degree.

The normal form of a quadratic function is of the form

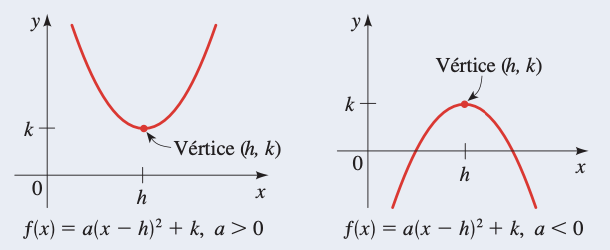
We see there's a maximum/minimum point at $x=h$

• If $a>0$, then the minimum of $f$ is $f(h)=k$
• If $a<0$, then the maximum of $f$ is $f(h)=k$

The apex point (maximum or minimum of a parabola) can be calculated from the standard form $ax^2+bx+c$, and is located at

• If $a>0$, then it is a minimum of $f$.
• If $a<0$, then it is a maximum of $f$.

A zero $c_i$ is each point of a polynomial that satisfies $f(c_i) = 0$

• They are solutions to $𝐏[x]=0$

1. Ceros. Factorizar la polinomial para hallar todos sus ceros reales; éstos son los puntos de intersección x de la gráfica.
2. Puntos de prueba. Hacer una tabla de valores para la polinomial. Incluir puntos de prueba para determinar si la gráfica de la polinomial se encuentra arriba o abajo del eje x sobre los intervalos determinados por los ceros. Incluir el punto de intersección y en la tabla.
3. Comportamiento final. Determinar el comportamiento final de la polinomial.
4. Graficar. Localizar los puntos de intersección y otros puntos que se encuen- tren en la tabla. Trazar una curva sin irregularidades que pase por estos puntos y exhibir el comportamiento final requerido

xychart-beta
    title "x to the power of 3"
    x-axis "x" -10 --> 10
    x-axis [-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    y-axis "y" -1000 --> 1000
    line [-1000, -729, -512, -343, -216, -125, -64, -27, -8, -1, 0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000]

  def generate_xychart(start, end, power):
    """
    Generates a custom XY chart format for x raised to a specified power.

    Args:
        start (int): Start of the range (inclusive).
        end (int): End of the range (inclusive).
        power (int): The power to which x is raised.

    Returns:
        str: The XY chart representation as a string.
    """
    # Generate x values
    x_values = list(range(start, end + 1))
    # Generate corresponding y values
    y_values = [x ** power for x in x_values]

    # Format the chart output
    chart_output = (
        f"xychart-beta\n"
        f"    title \"x to the power of {power}\"\n"
        f"    x-axis \"x\" {min(x_values)} --> {max(x_values)}\n"
        f"    x-axis {x_values}\n"
        f"    y-axis \"y\" {min(y_values)} --> {max(y_values)}\n"
        f"    line {y_values}"
    )

    return chart_output

  # Example usage
  start_range = -10
  end_range = 10
  power_value = 3
  chart = generate_xychart(start_range, end_range, power_value)
  print(chart)

We can transform a polynomial into a multiplication of simpler polynomials.

These terms 𝚛ₙ are called the $Root$ of the polynomial.

We observe that for a 2nd order polynomial

The roots of the square shape are of the form

Therefore

We can easily identify possible basic roots by the factors of the constant $c$.

• $P(x)$ : Dividendo
• $D(x)$ : Divisor
• $Q(x)$ : Cociente
• $R(x)$ : Residuo

If $P(x)$ is divided by $x-c$, then the residue is the value $P(c)$

$c$ is zero of $P$ if and only if $x-c$ is a factor of $P(x)$

if the polynomial $P(x)$ has whole coefficients, then all rational zero of it is of the form:

where $p$ is a factor of the constant coefficient $a_0$
and $q$ is a factor of the principal coefficient $a_n$

1. Make a list of candidates Use the Thm of Rational Zeros
2. Divide or Check With the Thm of the Factor

For every Polynomial function

with $n≥1$ has at least one zero $c ∈ ℂ$.

There are, then, n solutions $c_i ∈ ℂ$

If $z$ is a solution, the complex conjugate of $z$ is also a solution