22. Numbers - JulTob/Mathematics GitHub Wiki
$\color{#784}\text{"God created the numbers;}$
$\color{#784}\text{ all else is the work of man."}$
$\color{#784}\text{Leopold Kronecker}$
For mathematical analysis, a series of axioms are considered that define the simplest mathematical properties of numbers.
- Commutativity
- 𝓍+𝓎=𝓎+𝓍
- Associativity
- 𝓍+𝓎+𝓏 = (𝓍+𝓎)+𝓏 = 𝓍+(𝓎+𝓏)
- Distributivity
- 𝓍(𝓎+𝓏) = 𝓍𝓎+𝓍𝓏
- Neutral
- 1·𝓍 = 𝓍
- 𝓍+0 = 𝓍
- Negation
- ∀𝓍∃𝓎 : 𝓍+𝓎 = 𝓎+𝓍 = 0
- Reciprocal
- ∀𝓍∃𝓎 : 𝓍·𝓎 = 𝓎·𝓍 = 1
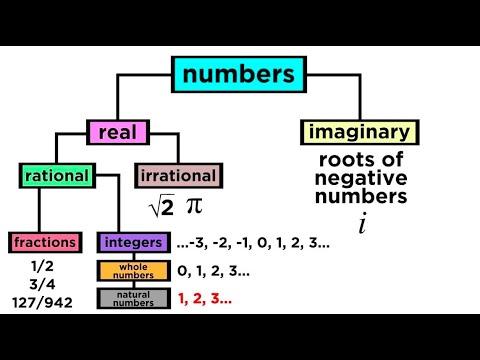
ℕ Naturals
ℕ⁺ Natural Positives
ℤ Integers
ℤ⁺ Positive Integers
ℤ⁰ Non-Negative Integers
ℤ𝕟 Modulo n
ℚ Rationals
ℚ⁺ Positive Rationals
ℚ⁰ Non-Negative Rationals
ℚ𝕟 n-Tuples of rational numbers
ℝ Reals
ℝ⁺ Positive Reals
ℝ⁰ Non-Negative Reals
ℝ𝕟 n-Tuples of reals
ℂ Complex (Complete) numbers
ℙ𝕟 Polynomials of degree nThe system of numbers is composed of many different elements.
We can develop these systems progressively, starting from...
The Empty set is the set with absolutely nothing in it. We can see we can develop the number systems just from the concept of the set itself.
First, we identify the empty set as the Zeroth element of the emergent system:
From this, we can identify the unit set as the set that contains the zeroth element, or the set that contains an empty set.
We then can go further by building a new set with all the sets we already have
In this way, we have developed the system of
Naturales
These are the numbers developed by
They represent discrete quantities.
They also establish order.
Some lively debate aside, the set of Natural
0 1 2 3 4 5
┠╶╶╶╂╶╶╶╂╶╶╶╂╶╶╶╂╶╶╶╂╶╶┈The simplest operation we introduce to the set is the Next operator. This operator maps the natural numbers into the consequent number.
As such, it follows the pattern we developed as creating the Natural set from the empty set.
next(0) = 1
next(1) = 2
next(2) = 3
next(3) = 4
next(4) = 5
...The addition of two natural numbers is always a Natural number.
𝚊,𝚋∈ ℕ
⟹ ∀(𝚊+𝚋)∈ ℕThe
Not all Naturals have a previous element. Zero does not have a previous inside the natural system.
Subtraction is the inverse of the Addition Operator, and also the iterative application of the
The application of the subtraction operator does not always fall inside the naturals.
𝚊,𝚋∈ ℕ
⟹ ¬∀(𝚊-𝚋)∈ ℕfor that we need...
Once we introduce the substraction operation we develop the
The ¬ symbol is the negation modifier (therefore, the negatives). We use this symbol to differentiate the negative element and the minus operation.
As we introduce the multiplication operator, and more specifically its' inverse: the division, we develop the Rational numbers
For which we defined the reciprocal element.
The elements that are not in the rational set are called Irrationals.
As such, these numbers have a decimal string of non-repeating digits, and cannot be expressed as a fraction, like π and √2.
They are introduced into the numbers as we develop polynomials. Many simple formulas return a complex answer such as
ℝ represents the set of all real numbers.
Tau is the perimeter value of the circle
pi is half the perimeter
As such, an Angle is a set inside ℝ defined as the possible values of an arc's amplitude proportional to the radius. The set of Radians (ℿ)
Golden Ratio
We can represent the set of real numbers with a line. With its points analogous to the Real Set of numbers, we can even use geometry to find solutions to problems.
┈──┼─┼─┼─┼─┼─┼─┼─┼─┈
0 1 2 3 4 5 6 7All points are "greater than" all points to the left, and "less than" every point to the right of themselves.
However, not all numbers are found as solutions to polynomials in the Real Numbers. Some solutions are found in the...
Maybe should be called Complete Numbers as any algebraic operation can be solved with them.
They are formed by a plane of numbers that exist in two dimensions.
We can describe any number as a linear combination of two basic lines, one in the Number system of the Reals, and one lateral to it, translated to the square root of negative 1:
We can also describe any number as a distance to the origin and an angle with the positive reals as the origin of the arc.
As such
As we can see, complex numbers are also essential for representing and working with trigonometric functions.
function Addition
n + m := next(n,m); -- next in m iterations
function Product
n × m = n + n .m. + n -- m iterations
- << Debt , Savings>>
- << Charge >>
- << Temperature >>
Positive numbers describe quantities greater than zero, and negative numbers less than zero. They show opposite directions.
-2 -1 0 1 2 3 4
┈┈╂────╂────╂────╂────╂────╂────╂─┈
Negative. Neutral. Positive
∀(𝚊-𝚋)∈ ℤ
x + b = a ⟺ (a,b) , [(a,b)] equivalente a [(c+a,c+b)]
ℕⅩℕ⟺ ℤ = [(0,0)],[(0,1)],[(1,0)] … ⟺ {0,-1,1…}
ℤ={…-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9…}
𝚊,𝚋∈ ℕ
𝚙,𝚚∈ ℤ
⟹ ∀(𝚊×𝚋)∈ ℕ
⟹ ∀(𝚙×𝚚)∈ ℤ
⟹ ∀(𝚊×𝚙)∈ ℤ
⟹ ¬∀(𝚊÷𝚋) ∈ ℕ‚ ℤ
⟹ ¬∀(𝚙÷𝚚) ∈ ℕ‚ ℤ∀𝑛∈ℕ ➝ ∃!𝑛⁺⁺ : 𝑛⁺⁺=𝑛+1
Todo número natural tiene un siguiente.
Inyectiva
𝙿(𝑛₀) & 𝙿(𝑛ᵢ)➝𝙿(𝑛ᵢ⁺⁺)⟹𝙿(ℕ)
z : (p,n) -- p,n ∈ ℕ
function Addition
z1 + z2 := (p1+p2, n1+n2);
function Product
z1 × z2 := (p1·p2 + n1·n2, p1·n2 + p2·n2)
procedure Order
z1 ≤ z2 := p1+n2 ≤ p2+n1
Maping
ℕ ⟶ ℤ
n (n+k,k) ≘ (n,0) -2 -1 0 1 2 3 4 …
┈╍╍╋╍╍╍╍╋╍╍╍╍╋╍╍╍╍╋╍╍╍╍╋╍╍╍╍╋╍╍╍╍╋╍╍┈
Rational := Integer : Natural
Fractions
Ratios
𝚍∈ ℤ 𝚌∈ ℕ⁰
x * b = a ⟺ (a,b) [(a,b)] Equivalente a [(ca,cb)]
ℤⅩℕ⁺⟺ ℚ = [(0,1)],[(1,1)],[(-1,1)],[(1,2)]… ⟺ {0,1,-1,½,…}
∀(𝚍÷𝚌)∈ℚ
⟹ 𝚍÷(-𝚌)⇔ -𝚍÷𝚌q : (c,d) -- c ∈ ℤ, d ∈ ℕ⁺
function Addition
q1 + q2 = (c1·d2 + c2·d1, d1·d2)
function Product
q1 × q2 := (c1·c2, d1·d2)
procedure Order
q1 ≤ q2 := c1·d2 ≤ c2·d1
Maping
ℤ, ⟶ ℚ
z (z,1)
ℤ/p= {0,1,2,…,(p-1)}
pℤ = {𝑘p∣ 𝑘∈ℤ}
Irrationals
-2 -1 0 1 2 3 4 …
┈┿╍╍╍╍┿╍╍╍╍┿╍╍╍╍┿╍╍╍╍┿╍╍╍╍┿╍╍╍╍┿╍╍┈
The Real but not Rationals
√2, √5, 𝜋, ℇ, 𝑒,
Reals
-2 -1 0 1 2 3 …
┈╋━━━━╋━━━━╋━━━━╋━━━━╋━━━━╋━┈
The Reals
1, √2, √5, 𝜋, ℇ, 𝑒, 5/7
-
Closure under Subtraction:
- The set
$( \mathbb{N} )$ is closed under addition and multiplication, meaning adding or multiplying two natural numbers results in another natural number. However, subtraction within$( \mathbb{N} )$ can result in numbers that are not in$( \mathbb{N} )$ . - Example:
$( 3 - 5 = -2 )$ , which is not a natural number. -
$( \mathbb{Z} )$ includes both positive and negative numbers as well as zero, making it closed under subtraction. This means any two integers subtracted from each other will yield another integer.
- The set
-
Representation of Opposites:
- In
$( \mathbb{Z} )$ , each positive integer has a corresponding negative (or additive inverse). For example, the integer$( 5 )$ has the inverse$( ¬5 )$ such that$( 5 + (¬5) = 0 )$ . - This property is important in algebraic operations and solutions to equations, as it allows for the “undoing” of addition through subtraction.
- In
-
Solving Equations with Unknown Differences:
- Many simple equations that involve subtraction (e.g., $( x + a = b )$) have solutions in
$( \mathbb{Z} )$ but not in$( \mathbb{N} )$ . For example, to solve$( x + 7 = 3 )$ ,$( x )$ must be$( -4 )$ , which is not in$( \mathbb{N} )$ but is in$( \mathbb{Z} )$ .
- Many simple equations that involve subtraction (e.g., $( x + a = b )$) have solutions in
-
Zero as a “Neutral Element” for Addition:
-
$( \mathbb{Z} )$ includes$( 0 )$ , which serves as the additive identity, meaning$( x + 0 = x )$ for any integer$( x )$ . This is foundational for algebraic operations and is necessary for defining additive inverses (negatives).
-
-
Closure under Division:
- While
$( \mathbb{Z} )$ is closed under addition, subtraction, and multiplication, it is not closed under division. Dividing two integers does not always yield an integer (e.g., $( 1 \div 2 = \frac{1}{2} )$), which is not in$( \mathbb{Z} )$ . -
$( \mathbb{Q} )$ , the set of all ratios of integers, is closed under division (except by zero). This allows us to solve a broader range of equations that involve division or fractions.
- While
-
Fractional Representation:
- Rational numbers allow for more precise representation of quantities. Many real-world values are not whole numbers, and
$( \mathbb{Q} )$ provides a way to represent parts of a whole or ratios. - For instance, half a unit (or $( \frac{1}{2} )$) is not representable in
$( \mathbb{Z} )$ , but it is in$( \mathbb{Q} )$ .
- Rational numbers allow for more precise representation of quantities. Many real-world values are not whole numbers, and
-
Solution of More General Equations:
- Equations like
$( 2x = 3 )$ (where $( x = \frac{3}{2} )$) have solutions in$( \mathbb{Q} )$ but not in$( \mathbb{Z} )$ . This expands the types of algebraic equations we can solve.
- Equations like
-
Density:
- The set
$( \mathbb{Q} )$ is dense on the number line, meaning between any two rational numbers, there exists another rational number. This property makes$( \mathbb{Q} )$ more flexible for approximation and analysis compared to$( \mathbb{Z} )$ or$( \mathbb{N} )$ , where "gaps" exist between consecutive elements.
- The set
In summary:
-
$( \mathbb{Z} )$ extends$( \mathbb{N} )$ by allowing subtraction and opposites, providing a complete set for additive operations. -
$( \mathbb{Q} )$ extends$( \mathbb{Z} )$ by including ratios, providing closure under division and allowing for precise fractional values.
These extensions make