🏗 Math Fundamentals

👶 $\text{\color{#19e}All mathematicians }$ $\text{\color{#19e}were very young }$ $\text{\color{#19e}when they }$ $\text{\color{#19e} were born.}$
－ $\text{\color{#19e}Ian Stewart, David Tall: The Foundations of Mathematics.}$

Mathematics begins at its very roots—with fundamental ideas that evolve into complex structures. This section lays the groundwork for understanding what mathematics is and how it develops.

🧩 What is mathematics?

Mathematics is often seen as a purely deductive discipline, built from a fixed set of axioms. As Felix Klein pointed out:

🌳 $\text{\color{#1ad}Many have thought that one must }$ $\text{\color{#1ad}teach all mathematics deductively }$ $\text{\color{#1ad}through [...] a definite }$ $\text{\color{#1ad}number of axioms }$ $\text{\color{#1ad} and deducing everything }$ $\text{\color{#1ad}from these by means of logic. }$
$\text{\color{#1ad}This method, which }$ $\text{\color{#1ad} some seek to maintain }$ $\text{\color{#1ad}on the authority of Euclid, }$ $\text{\color{#1ad}certainly does not correspond }$ $\text{\color{#1ad}to the historical development }$ $\text{\color{#1ad}of mathematics. }$
$\text{\color{#1ad}In fact, mathematics }$ $\text{\color{#1ad} has grown like a tree,}$ $\text{\color{#1ad}[that] sends its roots }$ $\text{\color{#1ad}deeper at the same time }$ $\text{\color{#1ad}that its branches }$ $\text{\color{#1ad}are spreading upwards. }$

• $\text{\color{#1ad}Felix Klein}$

🏗 In practice, $\color{Gold}Mathematics$ is the study of $\color{Aqua}\text{Emergent Structures}$: new properties, numbers, shapes, and theorems that arise when simple elements interact under certain rules.

[!IMPORTANT]

$\color{Aqua}Emergence$:

• 🛠 Refers to the appearance of new properties as we combine simple elements.
• 🛠 The attributes and objects that "emerge" from the interaction of elements forming certain $\color{Lime}structures$.
• New Structures: When basic elements (like numbers or points) interact, they form complex systems such as sets, functions, or even geometric shapes.
• 🪚 In linguistic terms: The $\color{#1bc}verbs$ that arise from the interactions of nouns.

$\color{Lime}Structure$:

The $\color{#888}rules$ or $\color{#927}framework$ behind these combinations. We look for patterns to see which structures are possible, impossible, or fundamental. Structure have rules governing these combinations.

🛠 Therefor $\color{Gold}Mathematics$ studies how objects interact and form larger entities, like $\color{#897}sets$ or $\color{#8A6}functions$ .

⚙️ One could argue that this encompasses absolutely everything.

🏛️ In a linguistic sense, mathematical nouns (like numbers) actually come from mathematical verbs (like counting). “Two” is meaningless without the act of counting. This interplay makes math both an inventive act (choosing how we formalize counting) and a discovering act (once we set the rules, certain truths become inevitable).

Consider the Fibonacci sequence. Starting with two numbers (0 and 1), a simple rule (each number is the sum of the two preceding ones) generates a sequence that appears in nature and art. Here’s a small Python snippet to generate it:

def fibonacci(n):
    """Return the first n Fibonacci numbers."""
    sequence = [0, 1]
    for _ in range(2, n):
        sequence.append(sequence[-1] + sequence[-2])
    return sequence

# Generate and display the first 10 Fibonacci numbers
print(fibonacci(10))

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

🪜 An $\color{#8B3}\text{Abstraction layer}$ is the conceptualization of a set of elements that conform an estructure without considering the building blocks of these elements. As one would conceptualize a wall as a set of bricks, without worrying if those bricks are ceramic or concrete. What determines a wall is not only the bricks, but their position and the binds of the mortar that ties them together.

🪜 The presence of elements can be derived from the attributes that belong to a lower layer of existence: an Abstraction Layer. A brick is itself a concrete shape of the ceramic elements. Going down to a fundamental necessary level we can find endless layers, or theoretically find this level absent of objects. Nothing can have properties, or so to say: absence is one of the properties present in the nothingness.

🧱 The parts that conform $\color{#8C4}Mathematics$ are denoted $\color{Gold}\text{structural⠀theorems}$, if these are found to exist. One could also argue that there is no need for elemental objects in mathematics, but some may be taken as $\color{Aqua}axioms$ in certain fields.

⛏ As such we see that emergent properties are derived from anything and nothing, therefore are both $\color{Gold}essential$ and $\color{Gold}fundamental$.

[!NOTE]

Recursive Nature:

• 🪞 Mathematics is itself a structure. Mathematics can examine itself, making it both a subject and an object of study​​​. Mathematics is itself necessary and essential. Unavoidable.

[!NOTE] 🧱 Numbers derive from verbs (actions) like counting or comparing, not nouns. A "two" exists only because we can count to it.

🧲 We can derive any descriptor from the properties of the elements (existing or not), explaining adjectives, and from interactions (to themselves, others, or the nothingness), the verbs. As such the essence to the noun is derived from naming these interactions as having their particular descriptors as interactions. These are emergent properties that characterized the being.

🔭 To be is a verb, therefore.

⚔️ Things are, in essence, interactions.

👤 The essence of the self is interaction. We are what we do.

🧩 The essence of constructing new elements is the $\color{Gold}arrangement$ (and therefore the systemic emergence) from previous elements. These elements are $\color{Aqua}axioms$ for a new level of reality, but also conclusions from their own birthing plane.

🍡 Example: The presence of two rocks, two apples, two persons... raises the property of duality.

🗝 Formal structures are the object of study in mathematics, these can have natural interpretations, or rather: Natural phenomena will (always) map to a certain mathematical object (known or unknown).

🪩 The obvious example is that an element from a complete ordered field can correspond to a point in a line or symbolically as an infinite string of decimal digits.

🏷 This is: a number can be a $\color{Red}point$, but is not just a point, or can be a $\color{Cyan}symbol$, but is not the symbol we use for representation, or can be an $\color{Emerald}operation$. A number can be the result of counting, even counting nothingnesses.

• ☝🏻 Numbers are operations:

• ✌🏻 The act of counting

• 🤟🏻 The cardinality of the set as counted

• 🖐🏻 Numbers are produced by verbs, functions.

• 🦶🏻 The core of maths is operations. Steps.

🏕 Math: invented or discovered?

Mathematics uniquely straddles the line between invention and discovery.

• Invention:

  • 💠 $\color{Aqua}Axioms$ are chosen. Axioms are the foundational assumptions from which we build entire systems (e.g., Euclidean geometry or set theory). With different axioms we invent different systems.

• Discovery:

  • 💍 Processes like $\color{Lime}\text{Arithmetics and Logic}$ reveal $\color{RedOrange}inferences$. They are discovered. We call these $\color{RedOrange}results$.

💡 In practice, math often feels like both:

• 💎 We invent a system (like Euclidean Geometry or Set Theory) by picking axioms.
• 🌈 Once in place, we discover surprising consequences (theorems) we didn’t anticipate.

🏘 Paradigms & Proof

🪵 At the heart of mathematics lies the process of logical deduction:

🪵 A mathematical theory is the collection of all the facts you can prove from a given set of starting $\color{Aqua}assumptions$.

🛖 If you can deduce from those axioms to reach a conclusion that wasn’t explicit in them already, that conclusion is called a $\color{RedOrange}theorem$.

🏗 The $\color{Gold}proof$ is the logical argument validating the theorem. The argument used to reach that conclusion. Inspecting the proof allows anyone to verify it.

🏠 So, what do mathematicians do?

1. Assume axioms.
2. Prove theorems.
3. Possibly invent new axioms if needed (e.g., the Axiom of Choice in Set Theory).

[!NOTE]

A puzzle to ponder:

Russell’s Paradox: “Does the set of all sets that do not contain themselves… contain itself?” Try to see how something as innocent as “the set of all sets” can lead to paradoxes (contradictions). This puzzle forced mathematicians to refine the axioms of set theory.

🛠 Why Emergence?

🔦 Math studies how objects interact and form larger entities, and any phenomenon might map to some math structure. This leads to:

• 🪔 Recursive Nature:
  • Math can study itself, producing fields like Mathematical Logic, Model Theory, and Metamathematics.
• 🕯️ Layers of Abstraction:
  • We begin with simple acts, like “counting apples”.
  • Then formalize these to “integers”.
  • Then extend into new conceptual realms like “negative numbers,” “fractions,” and “infinities” — All from an initial drive to count and compare.

[!IMPORTANT]
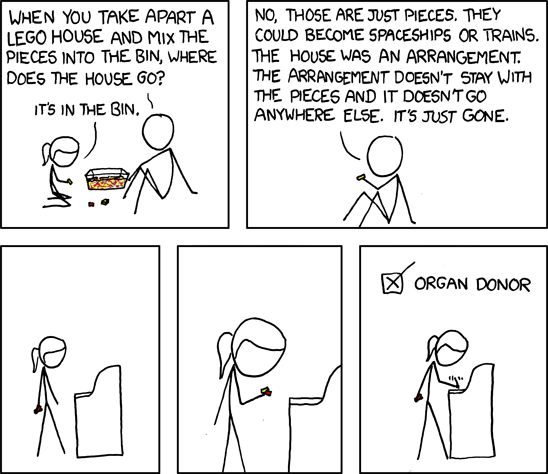
When you assemble LEGO bricks into a house, where exactly does the house exist? Disassemble the bricks and the “house” vanishes. This is an analogy for emergent structures: the “house” emerges from how the bricks are arranged, yet has no independent existence beyond them. This illustrates how emergent structures, while they have distinct properties, are not independent of their components.

🧸 Action Items

If you want to investigate these next topics now, you may find some surprising ideas waiting for you. We will study them in this wiki eventually, but first try using your own methods of invention and discovery we talked about.

Practice Basic Proof Techniques

• Direct proof, contradiction, induction.

[!CAUTION] Prove that there are infinitely many primes (Euler’s or Euclid’s argument).

Study Axiomatic Systems

• Peano Axioms (for natural numbers), Euclid’s postulates (for geometry).

[!CAUTION] Which Euclidean axiom fails on a curved surface?

Explore Foundational Paradoxes

• Russell’s Paradox, Zeno’s Paradoxes, Hilbert’s Grand Hotel.

[!CAUTION] “If a hotel has infinitely many rooms and they’re all full, can you still fit more guests?”

Reflect on Counting vs. Infinity

[!CAUTION] “Are there ‘more’ real numbers than integers?” (Cantor’s diagonal argument.)

🌱 Roots and Branches

Mathematics, from the fundamentals up, is a living tree. Roots growing deeper into axioms and philosophy, branches spreading outward into new theories and practical discoveries.

$\color{#009900}\text{“We are what we repeatedly do.”}$
– Attributed to Aristotle

[!TIP] Additional Reading & Links

• Ian Stewart & David Tall, The Foundations of Mathematics
• The book of Mathematics, akai publisher
• Russell’s Paradox Explanation