05 de junio - JoseA4718/Portafolio-I-2020 GitHub Wiki
Se inició la clase con el quiz #5
Quick Sort
Se trabaja partiendo el arreglo en dos y se aplica de nuevo quicksort en las particiones, para poder aplicarlo se calcula un pivote, luego de que se parte la lista se crean dos punteros en el indice mayor y otro en el menor. Se revisa si el elemento en el indice mayor es mayor que el pivot que se calculo y lo mismo con el pivote menor. En caso que esta comparación no aplique, se hace un swap entre los elementos. Este mismo proceso lo aplica con todos los elementos de la lista. En rendimiento es similar al merge sort.

Radix Sort
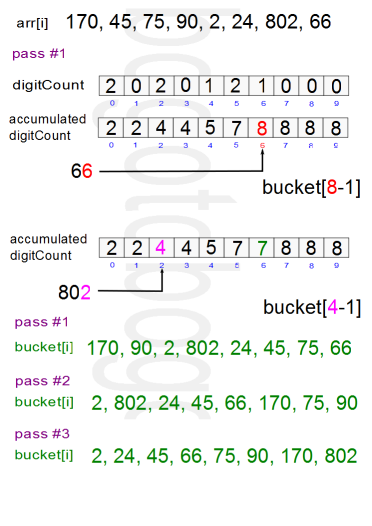
Este algoritmo de ordenamiento es diferente al resto de los algoritmos de ordenamiento. Del arreglo principal se crean dos sub-arreglos. El primero, de largo 9, se utiliza para contar cuántos elementos del array principal terminan en 0,1,2,3,4,5,6,7,8 o 9. Después, se van sumando los valores en el array, acumulando los anteriores a él.
Una vez hecho esto, se agarra el ultimo elemento del array original, nos fijamos en su dígito de las unidades. Vamos a la posición n que corresponda a la unidad del elemento seleccionado en el primer sub-array, y a su numero se le resta uno. Esta es la posición en la que vamos a colocar el elemento del array principal en el segundo sub-array y así seguidamente. Si se ocupa acceder a un elemento del primer sub-array otra vez, se le resta uno de nuevo al numero del contador, pues se acumulan las restas. Después de esta iteración, los elementos quedan acomodados en el segundo sub-array en orden de sus unidades. Por lo que se debe repetir con decenas, centenas, miles, et. Dependiendo de cuantos dígitos poseen los números.