Tree Basics

Author: James Dansie

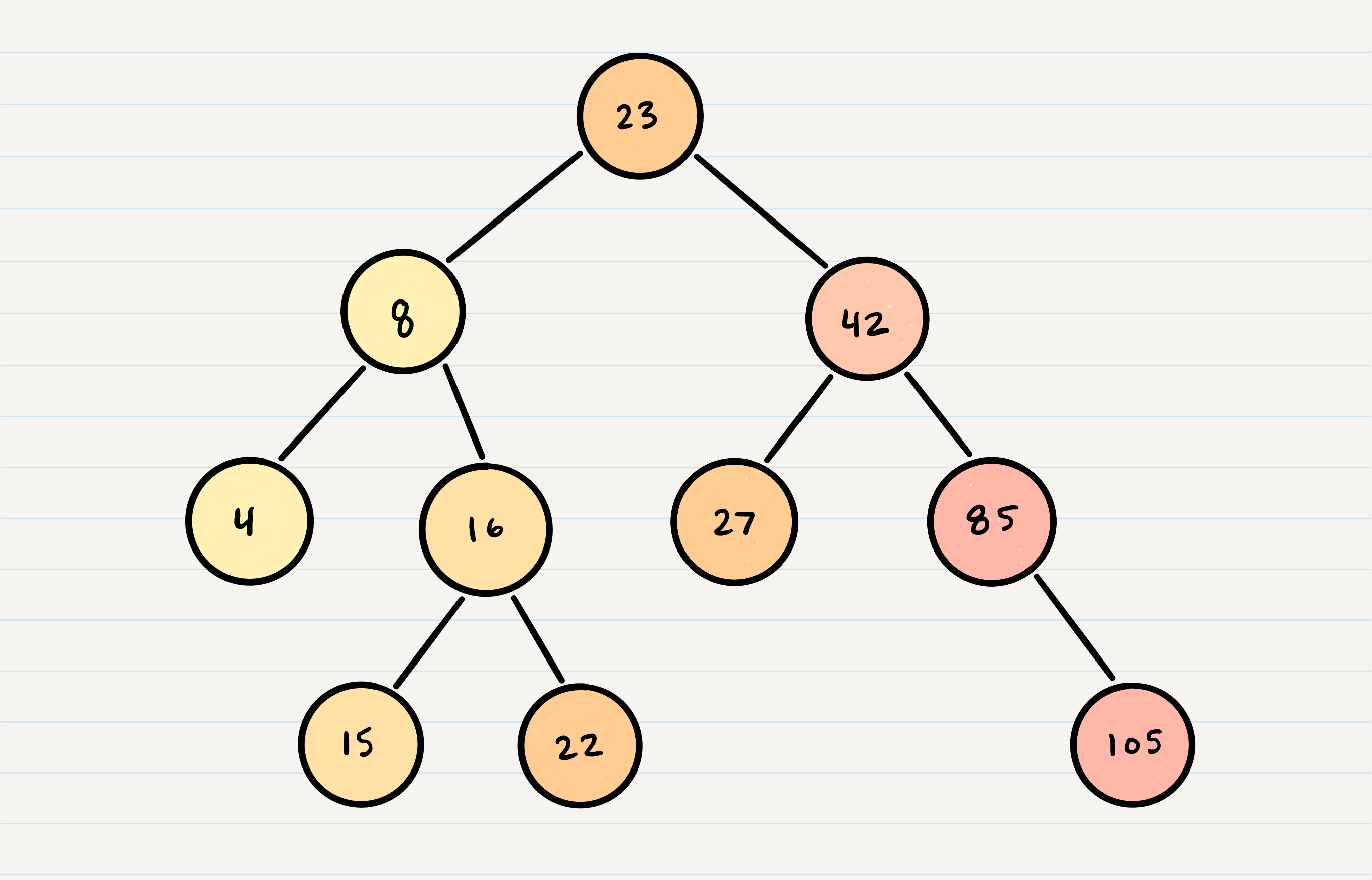
Trees are a data structure that are similar to linked lists. They have nodes that store a value, but they point at two additional nodes, instead of just one.

[1]

class Node {
    int value;
    Node left;
    Node right;
 
    Node(int value) {
        this.value = value;
        right = null;
        left = null;
    }
}

The extra nodes are usually called left and right.

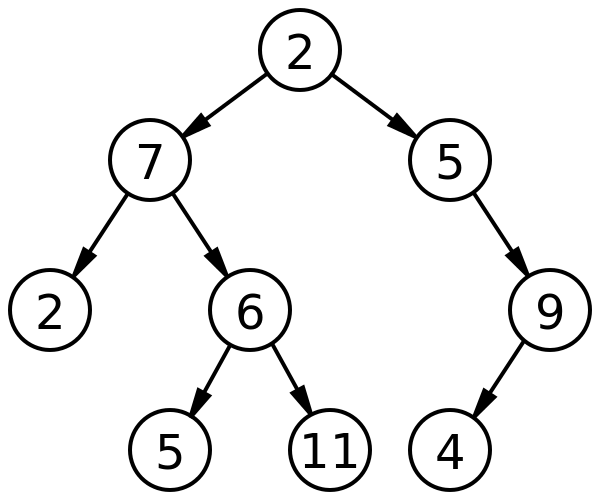
There are 3 depth first traversals; preorder, inorder, and postorder. For a preorder the above tree would be 1, 7, 2, 6, 5, 11, 5, 9, 4. For inorder it would be; 2, 7, 5, 6, 11, 5, 4, 9. For postorder it would be 5, 11, 6, 7, 4, 9, 5, 2. A good trick to figure this out quickly is; trace the tree from left to right along the outside of the left side. For preorder you write when whenever you pass the left of a node, for inorder you write whenever you go under a node, for postorder you write whenever you pass the right of a node.

Preorder [2]

Inorder [2]

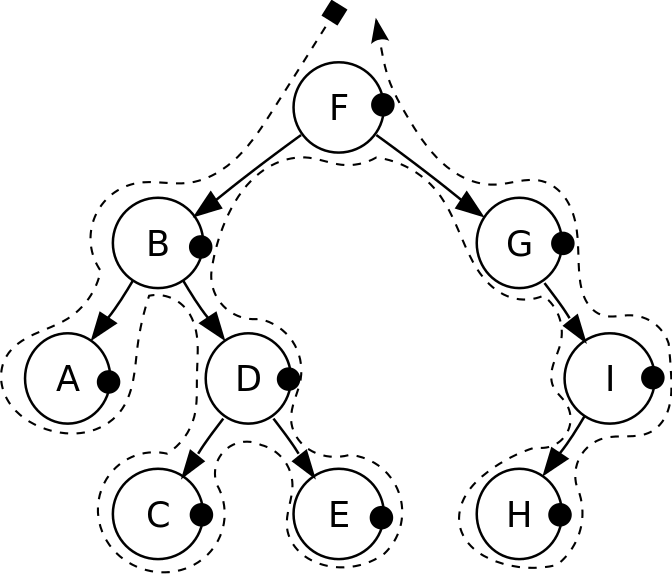
Postorder [2]

Traversing trees is always going to involve recursion. For an insertion into a tree we can use [1];

private Node addRecursive(Node current, int value) {
    if (current == null) {
        return new Node(value);
    }
 
    if (value < current.value) {
        current.left = addRecursive(current.left, value);
    } else if (value > current.value) {
        current.right = addRecursive(current.right, value);
    } else {
        // value already exists
        return current;
    }
 
    return current;
}

What this will do is search through the left and right nodes until it finds the value, or a free space (null) where it can put the node. The way that it searches for the null ensures that the binary search tree maintains it's ordering of smaller stuff of the left, and bigger stuff to the right [3].

---

References

1. https://www.baeldung.com/java-binary-tree
2. https://en.wikipedia.org/wiki/Tree_traversal
3. https://codefellows.github.io/common_curriculum/data_structures_and_algorithms/Code_401/class-15/resources/Trees.html