Struktur data diimplementasikan guna sebuah algoritma dapat mengoperasikan atau mengolah data secara efisien. Standar efisientitas suatu program bergantung dari kebutuhan program itu sendiri, apakah program tersebut butuh efisien dalam hal waktu (time complexity) atau dalam hal memori (space complexity). Dalam memilih algoritma dan struktur data yang tepat guna memenuhi kebutuhan program, maka diperlukan analisis untuk membandingkan satu algoritma dengan algoritma lainnya sehingga didapatkan algoritma paling efisien untuk diterapkan.

Contoh dari perlunya analisis struktur data adalah dalam kasus ARRAY VS LINKED LIST :

Dalam perbandingan di atas maka keduanya dapat digunakan dalam membentuk sebuah baris data, tetapi manakah yang terbaik?

Jika keperluan dari program adalah kecepatan dalam hal pengaksesan data maka array adalah yang terbaik, sedangkan jika keperluan program adalah kecepatan dalam melakukan manipulasi data (insert dan delete) maka linked-list yang terbaik. Namun, untuk mengetahui jawaban tersebut diperlukan analisis struktur data sehingga dua atau lebih struktur data dapat dibandingkan sehingga ditemukan struktur data yang terbaik.

Dua hal yang dianalisis dari suatu algoritma dan struktur data adalah kompleksitas waktu dan kompleksitas memori. Untuk melakukan analisis terhadap kompleksitas waktu maka dapat digunakan Asymptotic Analysis.

Asymptotic Analysis

Secara definisis Asymptotic Analysis atau Analisis Asimtotik adalah analisis performa (time and space complexity) dari suatu algoritma berdasarkan besaran input yang diberikan. Alasan penggunaan besar input untuk mengukur performa algoritma adalah:

1. Jika kita membandingkan algoritma A dan algoritma B, terdapat sebuah kemungkinan jika algoritma A akan lebih baik ketika diberikan suatu input tetapi ketika diberi input lain algoritma yang terbaik berubah menjadi algoritma B.
2. Jika kita membanfingkan algoritma A dan Algoritma B pada suatu mesin, terdapat kemungkinan hasil pengujian akan berbeda ketika kedua algoritma tersebut diuji di mesin lain.
3. Jika patokan kompleksitas waktu adalah running time dalam bentuk satuan waktu, maka spesifikasi dari suatu mesin akan mempengaruhi kecepatan dari sautu algoritma. Algoritma A akan dapat dikatakan cepat jika dijalankan pada mesin dengan spesifikasi tinggi tetapi akan dapat dikatakan lambat jika dijalankan pada mesin dengan spesifikasi rendah.

Berdasarkan 3 poin di atas maka running time tidaklah praktikal jika digunakan untuk menentukkan time complexity, untuk itu dapat digunakan Asymptotic Analysis. Berdasarkan asymptotic analysis maka running time dari suatu program dihitung berdasarkan berapa tahapan yang dilakukan oleh suatu algoritma dan struktur data dalam memproses input menjadi output.

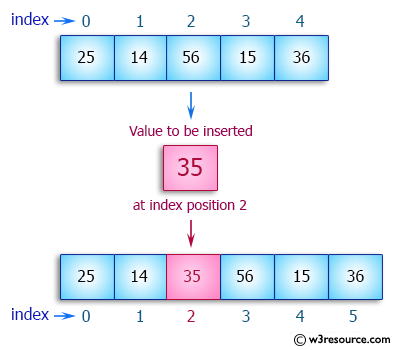
Perhatikan contoh di atas, gambar di atas adalah proses melakukan insert data ke dalam sebuah array. Untuk melakukan itu maka diperlukan pergeseran data pada index data baru akan diinsertkan. Pada contoh di atas data akan diisertkan pada index 2, sehingga index 2 dan setelahnya harus bergeser 1 index dan untuk melakukan itu dibutuhkan 3 tahapan. Kemudian, data baru diinsertkan dengan membutuhkan 1 tahapan. Maka running time dari algoritma tersebut dalam kasus ini adalah 4.

Dalam asymptotic analysis jumlah inputan dapan disimbolkan dengan n dan jumlah tahapan dapat dinotasikan dengan f(n). Dalam asymptotic analysis untuk melakukan membandingkan algoritma dan struktur tidak berpatokan pada hasil dari f(n) ketika diberikan suatu n, tetapi berpatokan pada pertumbuhan dari hasil f(n) ketika diberikan beragam nilai n yang berbeda-beda.

Contoh: Jika f(n) = $5^2$ + 6n + 12 maka besaran persen running time pada tiap ekspresi dalam fungsi tersebut adalah sebagai berikut

n	$5^2$	6n	12
1	21.74%	26.09%	52.17%
10	87.41%	10.49%	2.09%
100	98.79%	1.19%	0.02%
1000	99.88%	0.12%	0.0002%

Dapat dilihat pada tabel di atas, pada ketika jumlah n adalah 1, 12 memiliki presentase running time terbesar tetapi ketika n bertambah besar maka $5n^2$ menjadi ekspresi dengan nilai presentase running time terbesar sedangkan 12 berubah dengan memiliki presentase running yang sangat kecil. Melalui kondisi tersebut, maka untuk melakukan perbandingan algoritma dan struktur data tidak dapat digunakan hanya satu nilai n saja, karena terdapat kemungkinan berubah seperti contoh di atas.

Karena $5n^2$ mengambil alih mayoritas presentase dari running time, maka tidak akan menjadi masalah ketika 6n dan 12 dihilangkan. Dengan begitu f(n) saat ini menjadi: f(n) = $5n^2$, dengan menggunakan nilai tersebut maka didapatkan fungsi yang akan menghasilkan nilai yang hampir sama dengan nilai sebenarnya. Hasil yang mendekati nilai sebenarnya tersebut disebut dengan Asymptotic Complexity.