19 03 K Means Clustering - HannaAA17/Data-Scientist-With-Python-datacamp GitHub Wiki
01 Basics of k-means clustering
- Overcome the critical drawback of hierarchical clustering - runtime.
from scipy.cluster.vq import kmeans, vq
Step1: Generate cluster centers
kmeans(obs, k_or_guess, iter, thresh, check_finite)
obs: standardized observationsk_or_guess: number of clustersiter: number of iteration (default = 20)thres: threshold (default = 1e-5)check_finite: whether to check if observations only contain finite numbers (default = True)
Returns: cluster centers, distortion - Distortion = Sum of squared distances of points from cluster centers
Step2: Generate cluster labels
vq(obs, code_book, check_finite=True)
obs: standardized observationscode_book: cluster centers
Returnss: a list of cluster labels, a list of distortions
# Import the kmeans and vq functions
from scipy.cluster.vq import kmeans, vq
# Generate cluster centers
cluster_centers, distortion = kmeans(comic_con['x_scaled','y_scaled'](/HannaAA17/Data-Scientist-With-Python-datacamp/wiki/'x_scaled','y_scaled'),2)
# Assign cluster labels
comic_con['cluster_labels'], distortion_list = vq(comic_con['x_scaled','y_scaled'](/HannaAA17/Data-Scientist-With-Python-datacamp/wiki/'x_scaled','y_scaled'), cluster_centers)
# Plot clusters
sns.scatterplot(x='x_scaled', y='y_scaled',
hue='cluster_labels', data = comic_con)
plt.show()
02 How many clusters?
- NO absolute method to find number of clusters(k) in k-means clustering
- Elbow method
- Elbow plot: line plot between # of clusters and distortion
On distinct clusters
distortions = []
num_clusters = range(1, 7)
# Create a list of distortions from the kmeans function
for i in num_clusters:
cluster_centers, distortion = kmeans(comic_con['x_scaled','y_scaled'](/HannaAA17/Data-Scientist-With-Python-datacamp/wiki/'x_scaled','y_scaled'),i)
distortions.append(distortion)
# Create a data frame with two lists - num_clusters, distortions
elbow_plot = pd.DataFrame({'num_clusters': num_clusters, 'distortions': distortions})
# Creat a line plot of num_clusters and distortions
sns.lineplot(x='num_clusters', y='distortions', data = elbow_plot)
plt.xticks(num_clusters)
plt.show()
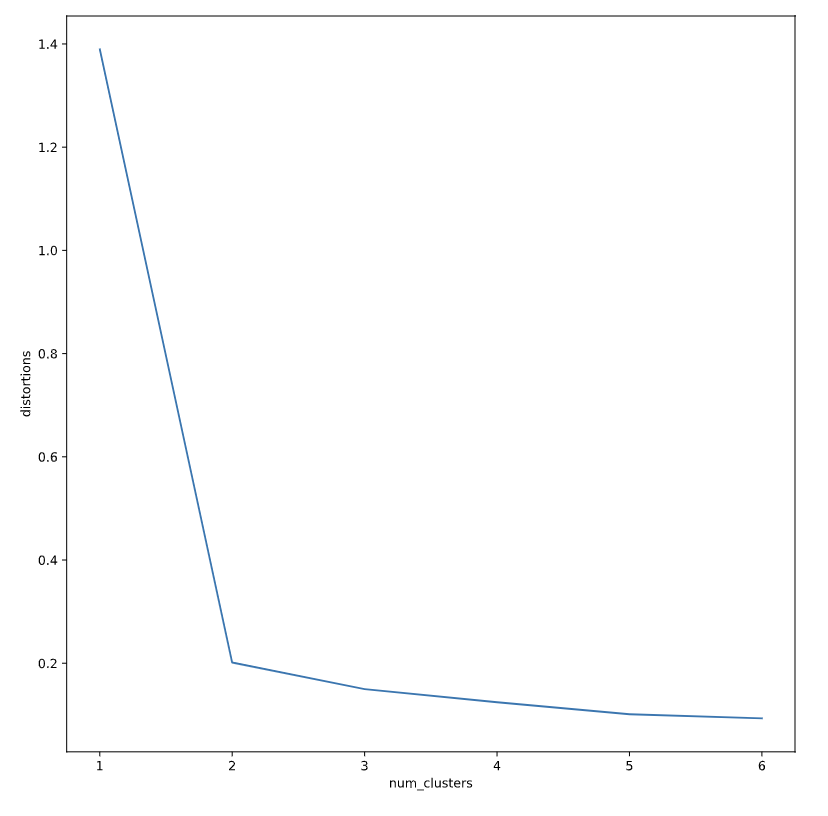
On uniformed clusters
- Does not always pinpoint how many k
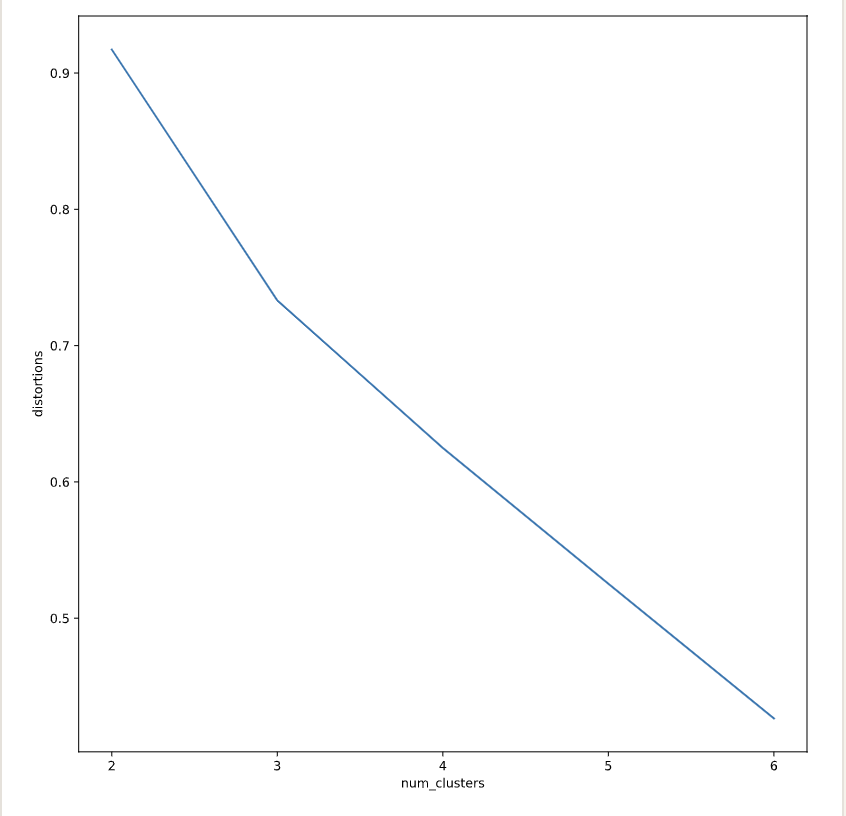
03 Limitations of k-means clustering
- Can not always find the right k
- Impact of seeds
- Process of defining the initial cluster centers is random.
- If the data has distinct clusters before clustering is performed, the effect of seeds will not result in any changes in the formation of resulting clusters.
- Biased towards equal size clusters
- Because the very idea of k-means clustering is to minimize distortions. This results in clusters that have similar areas and not necessarily the similar number of data points.