TF Complejidad Algorítmica - Gonan98/Compejidad-Algoritmica-TF GitHub Wiki
Trabajo Final - Complejidad Algorítmica
Introducción
La logística de almacenamiento trata tareas como colocar y guardar los aprovisionamientos recibidos, mantenerlos en correcto estado, así como procurar que el depósito de todos estos elementos redunde de manera positiva en la actividad de la empresa. No solo se trata de almacenar, también trata de que el empaquetamiento sea eficiente. Por ejemplo, no tiene mucho sentido colocar y guardar todo perfectamente, pero desordenado. En el área de logística de almacenamiento existen muchas funciones, incluso hay extensas investigaciones únicamente de este ámbito. Como funciones de logística de almacenamiento se tiene: actualizar los inventarios, registro del lugar en el que se encuentran almacenados, planificar las zonas de almacenamiento según el tipo de producto, facilitar la incorporación de los aprovisionamientos al proceso de producción e indicar como serán transportados cada uno de los aprovisionamientos.
El problema empaquetado es muy frecuente en este sector logístico. La frecuencia del problema se encuentra en la gestión de almacenamiento de productos para la optimización de espacio de objetos incurridos en el proceso de producción, al momento de transportar todos los productos en un paquete, se debe tener en cuenta que el espacio ocupado debe ser el máximo, ya que como resultado será la reducción de número de viajes realizados en transporte de dichos objetos de un lugar origen a su destino.
En este proyecto se implementará 3 algoritmos de empaquetamiento 3D para poder darle solución a un problema real, mostrando su funcionamiento y complejidad, así como también poner en práctica los conocimientos adquiridos en el curso en términos de complejidad algorítmica.
Índice
Objetivo del Estudiante (Student Outcome)
Este trabajo final tiene como objetivo poder aplicar algoritmos eficientes para la solucion de problemas reales. Tener un juicio crítico a la hora de tomar decisiones para soluciones en cualquier ámbito. Además reconocer responsabilidades éticas y profesionales.
Estado del Arte: De los algoritmos revisados para el trabajo
Algoritmo 1
El NFDH o Next-Fit Decreasing Height, es un algoritmo básico de empaquetamiento por niveles. En dos dimensiones funciona de manera sencilla. Las n piezas rectangulares (R) se ordenan de mayor a menor altura y se coloca el primero en la parte inferior izquierda de la plancha. Luego, se evaluará cada pieza Ri donde i = {1,2,3,...n-1}, si la pieza puede caber a la derecha de la anterior, entonces se colocará, sí no, se subirá un nivel sólo si el alto de la plancha es mayor al alto del nuevo nivel. Si esta última condición no se cumple, se creará una nueva plantilla y se colocara a R en la parte inferior izquierda de la plancha.
El algoritmo que se implementará para resolver la problemática sigue la heurística de empaquetamiento por estanterías, pasando de un espacio 2D a uno 3D. NFDH, o Next-Fit Decreasing Height, ordena las piezas de mayor a menor altura y se colocan continuamente para poder llenar el contenedor.

Una vez completado una fila de piezas, se generará una nueva fila en el máximo ancho que generó la anterior. Esto daría origen a la vista en tres dimensiones que es lo que busca el trabajo. Cuando un nivel de la estantería este lleno, se subirá un nivel y se repetirá el proceso. Cuando ya no pueda ingresar ninguna pieza más en el contenedor, se generará otro contenedor y colocaremos las piezas faltantes con el mismo método. Este algoritmo es rápido y puede procesar grandes cantidades de piezas, sin embargo, tiene un desperdicio de volumen muy grande.
(1) (2)
(2) (3)
(3)
Algoritmo 2
Este algoritmo es un empaquetamiento el cual empaca 3 cajas a partir de una caja ya empacada. Se tiene un conjunto de cajas para empaquetar, dichas cajas son ordenadas de manera decresciente respecto a su volumen, se coloca la primera en una esquina luego las 3 siguientes adyacentes a esta (una al eje X, otra al eje Y y la ultima al eje Z). Este algoritmo busca las posibles cajas que puedan caber al lado de su caja adyacente, esto quiere decir que también cambia la orientación de la caja a empaquetar. Cuando no puedan entrar mas cajas, se cambia de contenedor y se sigue empacando de la misma forma.
(vista de atras)
(vista lateral)
(vista de arriba)
Algoritmo 3
Este Algoritmo de empaquetamiento en 3D consiste en ordenar un conjunto de cajas de mayor a menor volumen, luego la primera caja debe ser coloca en la coordenada 0, 0, 0 y la siguiente caja se coloca encima. Se debe obtener el mayor ancho y largo, los cuales nos permitirán colocar las cajas en la siguiente fila y columna respectivamente. Cuando la caja sobrepase la altura del contenedor debe ser colocado en la siguiente fila, tomando en consideración el ancho máximo y así hasta terminar toda la columna. Finalmente al pasar a la siguiente columna se debe considerar el largo máximo como coordenada x de la caja. Este proceso se repetirá hasta colocar las demás cajas.
(1)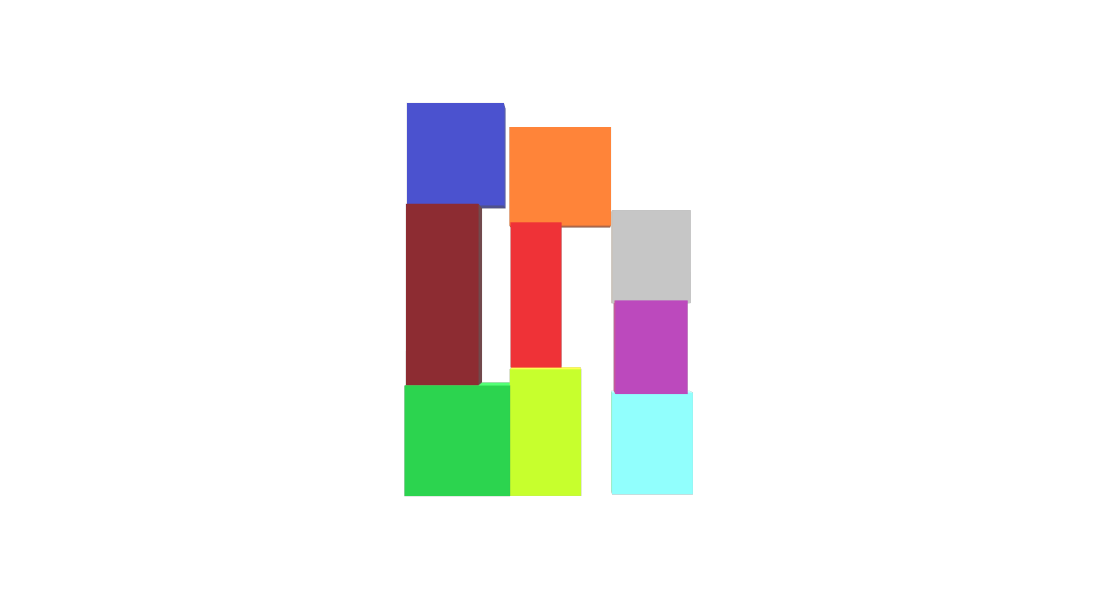 (2)
(2) (3)
(3) (4)
(4)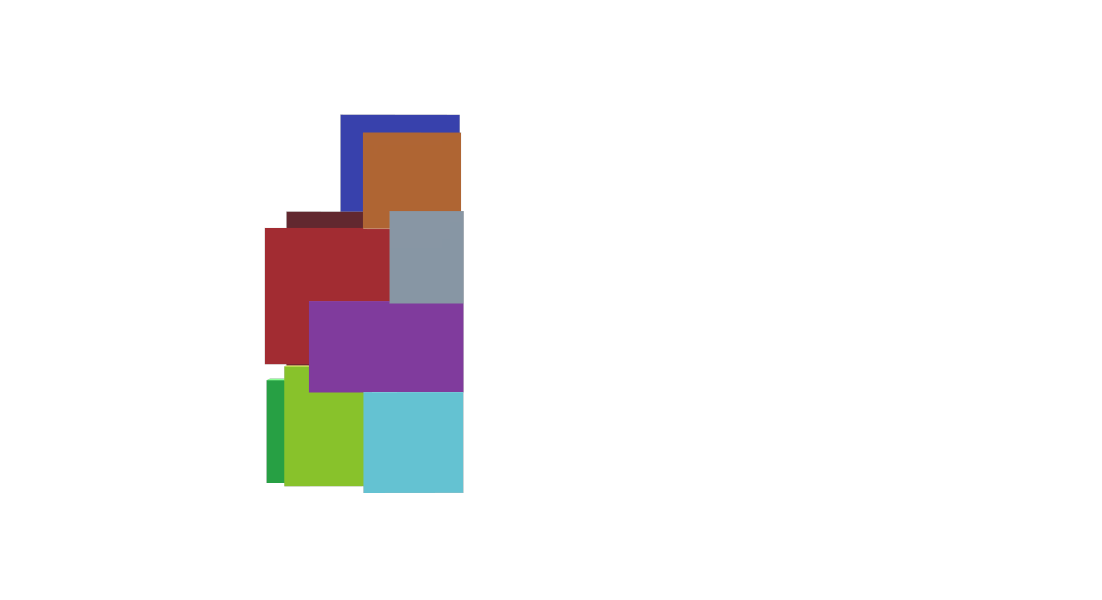
Aporte: Demuestra ética profesional en el ejercicio de la profesión
Algoritmo 1:
En el primer algoritmo, basado en la heuristica de estanterías, observamos una complejidad de n log(n) + n + const. El n log(n) representa el ordenamiento por alturas que necesita el algoritmo, el n representa el recorrido del arreglo, y el const son las condiciones para su posicionamiento en el contenedor; por lo que resulta ser O(n log(n)).
Algoritmo 2:
En el segundo algoritmo, se observa un empaquetado por bloque adyacente, al inicio todos los bloques se ordenan de mayor a menor con respecto a su volúmen, esto tiene una complejidad en el peor caso de O(n^2), luego con un for se ordena el primero, de ahi 3 fors siguientes ordenan uno adyacente al eje "X", otro al eje "Y" y por ultimo al eje "Z" todo esto tiene una complejidad en el peor caso de 6n^3 + n^2 + 30n + 4, en resumen O(n^3).
Algoritmo 3:
En el tercer algoritmo, basado en un ordenamiento por volumen, contemplamos que la complejidad es n log(n) + n + const. El n log(n) representa el ordenamiento por volumen que requiere el algoritmo, el n representa el recorrido del arreglo, y el const son las condiciones para su posicionamiento en el contenedor; por lo que resulta ser O(n log(n)).

Saber la complejidad algorítmica es de suma importancia en un contexto real, ya que podremos saber si con cantidades mayores de datos el algoritmo funcionará rápidamente. El conocer la complejidad algorítmica de cada algoritmo nos ayudará a escoger una mejor opción de solución para algún problema, buscando siempre que demoré la menor cantidad de tiempo.
Diseño de Aplicativo para Pruebas
Primer pseudocodigo:
def NFDH(arr, an, al, la)
OrdenarPorAltura(arr)
nC = 1
volumen = arr[0].ancho * arr[0].alto * arr[0].largo
arr[0].C = nC
xmax = arr[0].largo
xant = 0
zn = arr[0].alto
zant = 0
for i in range(1, len(arr))
volumen += arr[i].ancho * arr[i].alto * arr[0].largo
w = arr[i-1].y + arr[i-1].ancho + arr[i].ancho
if xant + arr[i].largo <= la
arr[i].C = nC
if w <= an
if xmax < xant + arr[i].largo xmax = xant + arr[i].largo
arr[i].x = xant
arr[i].y = arr[i-1].y + arr[i-1].ancho
arr[i].z = zant
elif arr[i].largo+xmax <= la
arr[i].x = xmax
xant = xmax
arr[i].y = 0
arr[i].z = zant
xmax = xmax + arr[i].largo
elif arr[i].alto + zn <= al
arr[i].x = 0
arr[i].y = 0
zant = zn
arr[i].z = arr[i].alto + zn
zn = arr[i].z
arr[i].C = nC
else
nC += 1
arr[i].C = nC
xmax = arr[i].largo
xant = 0
zn = arr[i].alto
zant = 0
elif arr[i].alto + zn <= al
arr[i].x = 0
arr[i].y = 0
zant = zn
arr[i].z = arr[i].alto + zn
zn = arr[i].z
arr[i].C = nC
else
nC += 1
arr[i].C = nC
xmax = arr[i].largo
xant = 0
zn = arr[i].alto
zant = 0
return arr, nC, volumen
Segundo pseudocodigo:
def Algoritmo2(cajas, contenedorW, contenedorH, contenedorL):
quickSort(cajas,0,len(cajas)-1)
n = len(cajas)
contenedor = 0
empacado = [False] * n
volumen = 0
while False in empacado:
for actual in range(n):
if not empacado[actual]:
contenedor+=1
cajas[actual].C = contenedor
empacado[actual] = True
volumen += cajas[actual].Volumen()
for i in range(n):
if empacado[i]: continue
if Cabe(cajas[i], cajas[actual], contenedorW, contenedorH, contenedorL) and not HaySuperpocicion(cajas, empacado, i):
cajas[i].x = cajas[actual].x + cajas[actual].Rotado()[0]
cajas[i].y = cajas[actual].y
cajas[i].z = cajas[actual].z
empacado[i] = True
cajas[i].C = contenedor
volumen += cajas[i].Volumen()
break
for j in range(n):
if empacado[j]: continue
if Cabe(cajas[j], cajas[actual], contenedorW, contenedorH, contenedorL) and not HaySuperpocicion(cajas, empacado, j):
cajas[j].x = cajas[actual].x
cajas[j].y = cajas[actual].y + cajas[actual].Rotado()[1]
cajas[j].z = cajas[actual].z
empacado[j] = True
cajas[j].C = contenedor
volumen += cajas[j].Volumen()
break
for k in range(n):
if empacado[k]: continue
if Cabe(cajas[k], cajas[actual], contenedorW, contenedorH, contenedorL) and not HaySuperpocicion(cajas, empacado, k):
cajas[k].x = cajas[actual].x
cajas[k].y = cajas[actual].y
cajas[k].z = cajas[actual].z + cajas[actual].Rotado()[2]
empacado[k] = True
cajas[k].C = contenedor
volumen += cajas[k].Volumen()
break
return cajas, contenedor, volumen
Tercer pseudocodigo:
def Algoritmo3(arr, an, al, la)
OrdenarPorVolumen(arr)
nC = 1
volumen = arr[0].ancho * arr[0].alto * arr[0].largo
arr[0].C = nC
xmax = arr[0].largo
ymax = arr[0].ancho
for i in range(1, len(arr))
volumen += arr[i].ancho * arr[i].alto * arr[i].largo
if arr[i-1].x + arr[i].largo <= la
if arr[i].ancho + arr[i-1].y <= an
if arr[i].alto + arr[i-1].z +arr[i-1].alto <= al
arr[i].C = nC
if xmax < arr[i-1].x + arr[i].largo xmax = arr[i-1].x + arr[i].largo
if ymax < arr[i-1].y + arr[i].ancho ymax = arr[i-1].y + arr[i].ancho
arr[i].x = arr[i-1].x
arr[i].y = arr[i-1].y
arr[i].z = arr[i-1].z + arr[i-1].alto
else
if arr[i].ancho + ymax <= an
arr[i].C = nC
arr[i].x = arr[i-1].x
arr[i].y = ymax
arr[i].z = 0
ymax = arr[i].y + arr[i].ancho
if xmax < arr[i-1].x + arr[i].largo xmax = arr[i-1].x + arr[i].largo
else
if xmax + arr[i].largo <= la
arr[i].C = nC
arr[i].x = xmax
arr[i].y = 0
arr[i].z = 0
xmax = xmax + arr[i].largo
ymax = arr[i].ancho
else
xmax = arr[i].largo
ymax = arr[i].ancho
nC += 1
arr[i].C = nC
else
if xmax + arr[i].largo <= la
arr[i].C = nC
arr[i].x = xmax
arr[i].y = 0
arr[i].z = 0
xmax = xmax + arr[i].largo
ymax = arr[i].ancho
else
xmax = arr[i].largo
ymax = arr[i].ancho
nC += 1
arr[i].C = nC
else
nC += 1
arr[i].C = nC
return arr, nC, volumen
Validación de Resultados y Discusión
Se realizó pruebas de memoria y tiempo para n = {100, 1000, 10000, 100000}, donde n es el numero de cajas a empaquetar. El resultado es el siguiente:

Obteniendo los siguientes gráficos:


Como se puede observar para el algoritmo 2 el tiempo de espera para 10000 y 100000 cajas es mayor a 1 hora, sin embargo los demás algoritmos promedian el segundo para 100000 cajas.
En uso de memoria, el algoritmo 1 es el que menor recursos de memoria solicita. Teniendo un máximo de 129 Mb aproximadamente cuando tenemos 100000 cajas.
Conclusiones y Trabajos Futuros
En conclusión, la complejidad algorítmica es igual de importante que la eficiencia del algoritmo. Ya que en un contexto real se procesan millones de datos, y estos tienen que ser procesados de la manera más rápida posible. Si un algoritmo es muy tardado no se puede hablar de una solución escalable en un ámbito real.
Conclusiones
Ventajas
El algoritmo 1 es sumamente rápido, esto debido a que recorre el arreglo solo una vez luego de haberlo ordenado. En tiempo es el que mejor rindió entre los tres algoritmos.
El algoritmo 2 busca la mejor forma de empaquetar un bloque, comprueba si cada bloque cabe con cada rotacion. De está forma busca reducir el espacio desperdiciado del contenedor.
El algoritmo 3 es relativamente rápido, ya que para una prueba de 100000 cajas lo puede empacar en un promedio de 1,5 segundos y comparado con los dos algoritmos restante, en cuestión de tiempo, este se ubica al medio
Desventajas
El algoritmo 1 desperdicia mucho espacio del contenedor. La heurística por alturas o estanterías hace que mucho espacio en algunas zonas no sean ocupados.
El algoritmo 2 realiza muchas comparaciones debido a que busca la mejor orientacion para empacar, lo que lo hace mucho más lento cuando se tiene que empaquetar miles de bloques.
El algoritmo 3 desperdicia gran cantidad de espacio que puede ser utilizado por cajas de menor volumen, esto se da cuando el algoritmo marca como límite el x máximo y el y máximo.
Anexos
Github: https://github.com/Gonan98/Compejidad-Algoritmica-TF
Bibliografía
Erlebach, T., & Persiano, G. (Eds.). (2006). Approximation and Online Algorithms: Third International Workshop, WAOA 2005, Palma de Mallorca, Spain, October 6-7, 2005, Revised Selected Papers (Vol. 3879). Springer.
Maarouf W.F., Barbar A.M., Owayjan M.J. (2008) A New Heuristic Algorithm for the 3D Bin Packing Problem. In: Elleithy K. (eds) Innovations and Advanced Techniques in Systems, Computing Sciences and Software Engineering. Springer, Dordrecht https://link.springer.com/chapter/10.1007/978-1-4020-8735-6_64#citeas