Multiplication - Falmouth-Games-Academy/comp310-wiki GitHub Wiki
The 6502 architecture has no multiplication instruction, so when the multiplication is required, an explicit method must be performed.
The simplest method to multiply two positive integers, and the easiest to understand, is to repeat an addition function.
In pseudo code:
int m, n
result = 0
count = 1
Do While count <= m
result += n
loop
return result
Or in assembly language:
; Multiply positive integers m and n
LDA #0 ; Start with a zero value in the accumulator register
LDX #m ; Load into the X register the number of times to loop
CLC ; Ensure the carry flag is clear to ensure that an additional
; increment isn't performed [1]
Loop:
ADC #n ; Add the value of n to the accumulator register
DEX ; Decrement the X register
BNE Loop ; If the zero flag has _not been set by the DEX (X!=0), then
; branch to Loop:
STA $result ; Result is now stored in the accumulator register
In the context of 6502 game development, taking advantage of the addition instruction can be a sound method as it is likely that a positive integer will be used. e.g. number of enemies, damage or ammunition of a weapon, number of lives remaining, or score. However, in terms of efficiency, this method will grow the number of CPU cycles needed proportionately to the factors giving 9 + (n * 7) cycles or O(n). With high numbers, this may prove to be too expensive.
Bit shifting
By taking the binary representation of a number and shifting the bits to the left or to the right, The binary representation of either the multiple or division of two can be quickly found. With the 6502 this is limited by the 8-bit memory limitation, giving an upper value of 255. this means that in a single bit shift instruction, the maximum number that can be multiplied by 2 is 127. In terms of division, the nature of a binary number representing integers dictates that an odd number being bit shifted right will result in only the whole number portion of the required result, the rightmost bit being thrown away as shown by reading the below example bottom to top. A value of 254 will return the same binary result as 255 were they to be bit shifted right.
01111111 = 127
///////
11111110 = 254
However, there are workarounds when working with 8-bit values that allow us to use the carry flag to link two 8-bit values together as a 16-bit representation (or more) which is covered in the 16-bit values section below.
6502 instructions
Bit shifting in the assembly language can be done by using any of four instructions.
ROL - Rotate Left. Moves each of the bits one place to the left. The newly empty bit 0 is filled with the current value of the carry flag, and the old bit 7 becomes the new carry flag value.
ROR - Rotate Right. Moves each of the bits one place to the right. The newly empty bit 7 is filled with the current value of the carry flag, and the old bit 0 becomes the new carry flag value.
ASL - Arithmetic Shift Left. The same as ROL except that bit 0 is given a value of 0.
LSR - Logical Shift Right. The same as ROR except that bit 0 is given a value of 0.
[2] [3]
When using bit shifting to quickly multiply or divide an 8-bit value by 2, it is best to use ASL or LSR over the rotation instructions as the contents of the carry flag which will populate the subsequently empty bit without a further instruction or knowledge of the context.
It follows that to multiply or divide quickly by powers of two, these instructions can be repeated
; Multiply by 8
ASL VALUE ; Multiply by 2
ASL VALUE ; Multiply by 2*2
ASL VALUE ; Multiply by 2*2*2
[4]
16-bit values
When values larger than that which can be represented by a single byte are needed, two bytes can be used together to represent a 16-bit number. After performing a mathematical instruction upon the value in the low byte, the value in the carry flag should be added to the high byte to continue the 16-bit value representation.
Little endian:
high byte low byte
128 64 32 16 8 4 2 1 128 64 32 16 8 4 2 1
<--Carry flag value
16-bit binary value = low bit value + (256 * low bit value)
Note that care should be taken as to the computation order so as the carry flag correctly carries a carried value to the correct position in a subsequent 8-bit value. This method can also be used to represent values between zero and one by treating the high and low bytes as if they have a decimal point between them. In practice, whole number values can be read from the high byte, and the truncated low byte is used for subtle computations. More than two bytes may also be used.
Binary multiplication
Useful multiplication methods
Many multiplication methods exist that can be used for a binary number system by a computer. Booth's Algorithm scans three bits at a time, searching for and efficiently processing strings of 0's or 1's [9], and modified versions can attempt to synthesise such strings and carry a common overlap [7], or over iterative arrays [14]. Some methods change the representation to using a different base or radix other than binary [13], bit shifting the input binary numbers [6] or by adapting squaring algorithms using the formula A*B = ((A+B)/2)^2 - ((A-B)/2)^2 to use a binary method [12]. Rational approximation, CORDIC (an acronym for Coordinate Rotation Digital Computer and is a method of computing transcendental functions that uses mostly shifts and adds i.e. very few multiplications and division [15]), and large tables can be used although no single method can be said to be correct for every system or circumstance [8].
Look up table
With limited resources, a viable alternative for a system with a limited pool of values (e.g. if the total number of bombs are needed where there are between 10-15 enemies with between 4-7 bombs each), is a hard-coded lookup table. The cost of implementing an expensive multiplication algorithm must be weighed against the potential cost of storing all possible answers within the memory of the system.
At the cost of some execution time and a little algebra, the stored table can be made much smaller. By considering the difference between squares, and using the squaring algorithm shown previously (sometimes rearranged to a*b = (a + b)^2/4 - (a - b)^2/4), we can do a multiplication with an addition, two subtractions, a couple of right shifts, and a couple of lookups in a table of squares [4].
An example of a used look up table can be seen here
Vedic multiplication methods
Vedic mathematics (Vedic is derived from the word veda which means the store-house of all knowledge) offer low power and high speed algorithms that are much faster than conventional multipliers [11]. This ancient Indian system of mathematics is based on 16 Vedic Sutras. Examples of multiplication methods include the Urdhva Tiryakbhyam Sutra and Nikhilam Sutra.
The Urdhva Tiryakbhyam Sutra can be shown for a decimal system as:
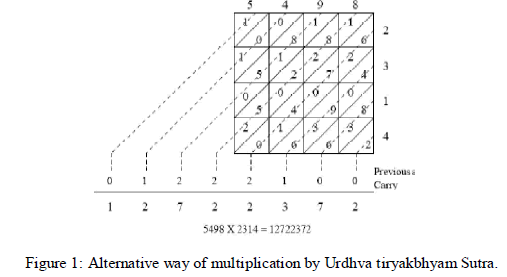
And a binary system as:
; For multiplying two 4-bit binary numbers
; a3 a2 a1 a0 and b3 b2 b1 b0
; Where cn refers to the carry from the previous or nth step
r0 = a0 b0 ; 1
c1 r1 = a1 b0 + a0 b1 ; 2
c2 r2 = c1 + a2 b0 + a1 b1 + a0 b2 ; 3
c3 r3 = c2 + a3 b0 + a2 b1 + a1 b2 + a0 b3 ; 4
c4 r4 = c3 + a3 b1 + a2 b2 + a1 b3 ; 5
c5 r5 = c4 + a3 b2 + a2 b3 ; 6
c6 r6 = c5 + a3 b3 ; 7
; With c6 r6 r5 r4 r3 r2 r1 r0 being the binary representation of the answer
This is shown visually as:
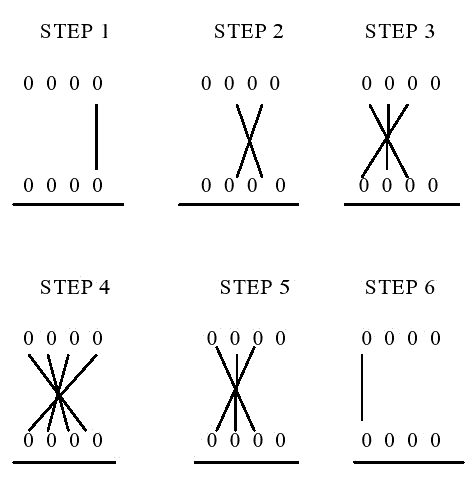
[10]
An alternative is the Nikhilam Sutra which constructs the upper and lower portions of the answer, by finding the nearest base (in this case 100), and using the other values difference from that base value to subtract from for the upper portion of the answer, and the much simpler multiple of both differences for the lower portion of the answer. Note that the arrows below indicate the value to be subtracted from the starting value:
Multiplication using Nikhilam Sutra [6]
Negative numbers
Most examples of code given so far have been designed to work with unsigned number values. Bit shifting instructions like LSR and ROR are not sign preserving [4]. The simplest solution is to compute the sign of the result by either examining it's high bit or to subtract it from zero, compute the multiple as if they are both positive, then apply the computed sign to the result [4].
Example code for the 6502 as shown on the NesDev website [5]
The Russian Peasant algorithm [5]
Tepples
;;
; Multiplies two 8-bit factors to produce a 16-bit product
; in about 153 cycles.
; @param A one factor
; @param Y another factor
; @return high 8 bits in A; low 8 bits in $0000
; Y and $0001 are trashed; X is untouched
.proc mul8
prodlo = $0000
factor2 = $0001
; Factor 1 is stored in the lower bits of prodlo; the low byte of
; the product is stored in the upper bits.
lsr a ; prime the carry bit for the loop
sta prodlo
sty factor2
lda #0
ldy #8
loop:
; At the start of the loop, one bit of prodlo has already been
; shifted out into the carry.
bcc noadd
clc
adc factor2
noadd:
ror a
ror prodlo ; pull another bit out for the next iteration
dey ; inc/dec don't modify carry; only shifts and adds do
bne loop
rts
.endproc
Assuming no page crossings and zero page, this routine takes 137-169 cycles, not counting the JSR to call it. (Each non-zero bit in A adds 4 cycles [5].
Tepples unrolled
; @param A one factor
; @param Y another factor
; @return low 8 bits in A; high 8 bits in Y
mul8_multiply:
lsr
sta prodlo
tya
beq mul8_early_return
dey
sty factor2
lda #0
.repeat 8, i
.if i > 0
ror prodlo
.endif
bcc :+
adc factor2
:
ror
.endrepeat
tay
lda prodlo
ror
mul8_early_return:
rts
The code takes up 70 bytes and runs in 120 cycles or less [5].
Bregalad
;8-bit multiply
;by Bregalad
;Enter with A,Y, numbers to multiply
;Output with YA = 16-bit result (X is unchanged)
Multiply:
sty Factor ;Store input factor
ldy #$00
sty Res
sty Res2 ;Clear result
ldy #$08 ;Number of shifts needed
- lsr A ;Shift right input number
bcc + ;Check if bit is set
pha
lda Res2
clc
adc Factor
sta Res2 ;If so add number to result
pla
+ lsr Res2 ;Shift result right
ror Res
dey
bne -
lda Res
ldy Res2
rts
Assuming no page crossings and zero page, this routine takes 184-320 cycles, not counting the JSR to call it. (Each non-zero bit in A adds 17 cycles [5].
Frantik
; Multiply two bytes in memory using Russian peasant algorithm
; by frantik
; Accepts: value1 and value2, labels for bytes in memory
; value2 should ideally be the lesser of the two input values
; for increased efficiency
; Uses: $00, $01, $02 for temporary variables
; Returns: 16 bit value in $00 and $01
.macro multiply value1, value2
ret = $00 ; return value
temp = $02 ; temp storage
lda #$00 ; clear temporary variables
sta ret
sta ret+1
sta temp
lda value2
bne +end"
jmp +start:
-loop:
asl value1 ; double first value
rol temp ; using 16bit precision
lsr value2 ; halve second vale
+start:
lda value2 ;
and #01 ; is new 2nd value an odd number?
beq -loop: ;
clc ; if so, add new 1st value to running total
lda ret ;
adc value1 ;
sta ret ;
lda ret+1 ;
adc temp ;
sta ret+1 ;
lda value2 ;
cmp #01 ; is 2nd value 1? if so, we're done
bne -loop: ; otherwise, loop
+end:
.endm
Assuming no page crossings and zero page, this routine takes 17-403 cycles, though it is an in-place macro generating 46 bytes of new code each time it is used [5].
Summary
Given the limited resources of the NES architecture, and the potential limited range of required multiplications in the context of game development, repeating additions, bit shifting, or the use of a look up table is highly recommended. Especially if using a squaring algorithm to spread the cost between stored values in memory and some computation cycles. As an exercise, and for the specific use cases with uncertain parameters, Vedic mathematics offers interesting solutions. Although with the computation cost, effort should be made to redesign the use case to use an simpler method.
References
[1] Andrew John Jacobs - Obelisk personal web page algorithms
[2] Andrew John Jacobs - Obelisk personal web page instruction reference
[3] Neil Parker - Apple II The 6502 Instruction Set Decoded
[4] Neil Parker - Apple II Multiplying and Dividing on the 6502
[5] Nes Dev - 8-bit Multiply
[6] Dhillon, Harpreet Singh, and Abhijit Mitra. "A reduced-bit multiplication algorithm for digital arithmetic." International Journal of Computational and Mathematical Sciences 2.2 (2008)
[7] Ma, G-K., and Fred J. Taylor. "Multiplier policies for digital signal processing." IEEE Assp Magazine 7.1 (1990): 6-20
[8] Goldberg, David. "What every computer scientist should know about floating-point arithmetic." ACM Computing Surveys (CSUR) 23.1 (1991): 5-48
[9] Booth, Andrew D. "A signed binary multiplication technique." The Quarterly Journal of Mechanics and Applied Mathematics 4.2 (1951): 236-240
[10] Tiwari, Honey Durga, et al. "Multiplier design based on ancient Indian Vedic Mathematics." SoC Design Conference, 2008. ISOCC'08. International. Vol. 2. IEEE, 2008
[11] Kumar, G. Ganesh, and V. Charishma. "Design of high speed vedic multiplier using vedic mathematics techniques." International Journal of Scientific and Research Publications 2.3 (2012): 1
[12] Chen, Tien Chi. "A binary multiplication scheme based on squaring." IEEE Transactions on Computers 100.6 (1971): 678-680
[13] Seidel, P-M., Lee D. McFearin, and David W. Matula. "Binary multiplication radix-32 and radix-256." Computer Arithmetic, 2001. Proceedings. 15th IEEE Symposium on. IEEE, 2001.
[14] Majithia, Jayanti C., and Reuven Kitai. "An iterative array for multiplication of signed binary numbers." IEEE Transactions on Computers 2 (1971): 214-216.
[15] Walther, John S. "A unified algorithm for elementary functions." Proceedings of the May 18-20, 1971, spring joint computer conference. ACM, 1971.