Binary Coded Decimal - Falmouth-Games-Academy/comp310-wiki GitHub Wiki
This is a process for converting decimal numbers into their binary equivalents [1]. This is useful for us as programmers as it means that we can program using the form factor we are more familiar with as humans. This helps to open up our possibilities as we can then make more complex systems where we may not know the numbers being used.
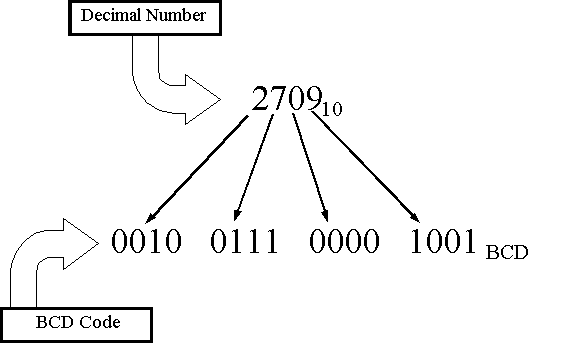
BCD works by taking each digit from the decimal number given and converting it to the binary equivalent [2]. All the binary numbers generated are then combined to form a binary number. For example:
To clarify BCD is not the same as representing the same number in binary form. For the example above, 2709 in binary would be 101010010101 [3], which would require 12 bits to store [4]. First the number is split into individual digits (e.g. 2, 7, 0, 9) [1].
Each digit is converted into the binary equivalent, 4 bits can store up to 1111 which, using the table below, is (2^3 + 2^2 + 2^1 + 2^0 = 8 + 4 + 2 + 1 = 15 (decimal). Which is enough to show all 9 single digits of decimal.
The table below [1] shows the conversion of a decimal number into a 4 bit binary number. The binary representation has been added to show which bit each of the 4 bits represents.
| Binary Power | 2^3 | 2^2 | 2^1 | 2^0 |
|---|---|---|---|---|
| Binary Weight | 8 | 4 | 2 | 1 |
| Binary Representation | 1000 | 0100 | 0010 | 0001 |
Using the above table again, working backwards, we can convert each of the 4 decimal digits of 2709.
- 2 = 8x0 + 4x0 + 2x1 + 1x0 = 0010
- 7 = 8x0 + 4x1 + 2x1 + 1x1 = 0111
- 0 = 8x0 + 4x0 + 2x0 + 1x0 = 0000
- 9 = 8x1 + 4x0 + 2x0 + 1x1 = 1001