Сортировка слиянием в Java

Сортировка слиянием — это алгоритм сортировки, который рассматривается как пример стратегии «разделяй и властвуй». В данном алгоритме массив изначально делится на две равные половины, а затем они объединяются в отсортированном виде. Мы можем думать об этом как о рекурсивном алгоритме, который непрерывно разбивает массив пополам до тех пор, пока его нельзя будет разделить дальше. Это означает, что если массив станет пустым или в нем останется только один элемент, деление остановится, т.е. базовым случаем является остановка рекурсии. Если массив состоит из нескольких элементов, мы разделяем массив на половины и рекурсивно вызываем сортировку слиянием для каждой из половин. Наконец, когда обе половины отсортированы, применяется операция слияния. Операция слияния — это процесс взятия двух меньших отсортированных массивов и объединения их для создания большего массива.

Подробный алгоритм сортировки

Для решения задачи сортировки эти три этапа выглядят так:

1. Сортируемый массив разбивается на две части примерно одинакового размера. Рекурсивное разбиение задачи на меньшие происходит до тех пор, пока размер массива не достигнет единицы (любой массив длины 1 можно считать упорядоченным);
2. Каждая из получившихся частей сортируется отдельно, например — тем же самым алгоритмом;
3. Два упорядоченных массива половинного размера соединяются в один. Основную идею слияния двух отсортированных массивов можно объяснить на следующем примере. Пусть мы имеем два уже отсортированных по возрастанию подмассива. Тогда: на каждом шаге мы берём меньший из двух первых элементов подмассивов и записываем его в результирующий массив. Счётчики номеров элементов результирующего массива и подмассива, из которого был взят элемент, увеличиваем на 1. Когда один из подмассивов закончился, мы добавляем все оставшиеся элементы второго подмассива в результирующий массив.

Пример работы сортировки слиянием

Рассмотрим массив:

arr[] = {38, 27, 43, 3, 9, 82, 10}

Сначала проверяем, меньше ли левый индекс массива, чем правый индекс, если да, то вычисляем его среднюю точку:

Теперь, как мы уже знаем, сортировка слиянием сначала итеративно делит весь массив на равные половины, если не достигнуты атомарные значения. Здесь мы видим, что массив из 7 элементов разбит на два массива размером 4 и 3 соответственно:

Теперь снова найдем, что левый индекс меньше правого индекса для обоих массивов, если нашли то, затем снова вычисляем средние точки для обоих массивов:

Теперь разделим эти два массива еще на две половины, пока не будут достигнуты атомарные единицы массива и дальнейшее деление станет невозможным:

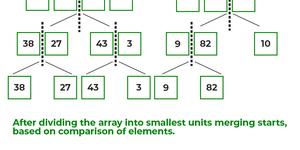
После разделения массива на наименьшие единицы снова начинаем объединять элементы на основе сравнения размеров элементов. Во-первых, сравниваем элемент для каждого списка, а затем объединяем их в другой список в отсортированном виде:

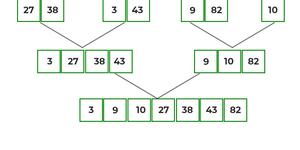
После окончательного слияния список будет выглядеть так:

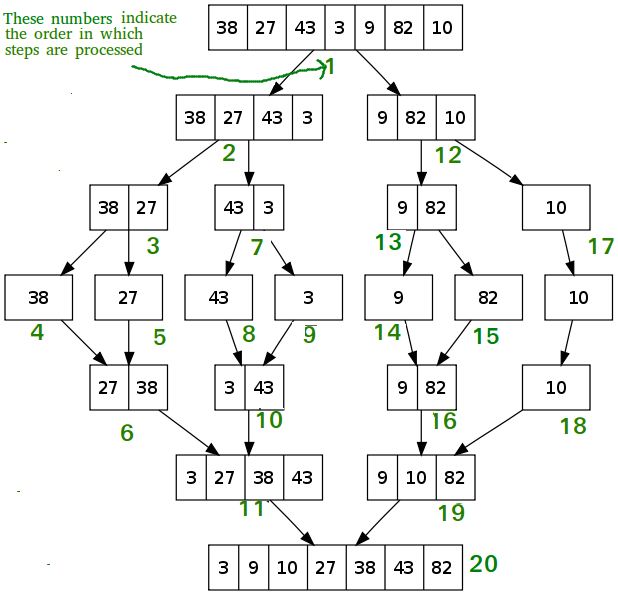
На следующем рисунке показана общая картина работы алгоритма сортировки слиянием для вышеуказанного массива:

Реализация алгоритма сортировки слиянием на Java

    // Первый подмассив это arr[l..m]
    // Второй подмассив это arr[m+1..r]
    void merge(int arr[], int l, int m, int r)
    {
        // Найдите размеры двух подмассивов, которые нужно объединить
        int n1 = m - l + 1;
        int n2 = r - m;
  
        //  Создание временных массивов
        int L[] = new int[n1];
        int R[] = new int[n2];
  
        // Копировать данные во временные массивы
        for (int i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];
  
        // Объединить временные массивы
  
        // Начальные индексы первого и второго подмассивов
        int i = 0, j = 0;
  
        // Начальный индекс объединенного массива подмассивов
        int k = l;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            }
            else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }
  
        // Скопируйте оставшиеся элементы L[], если они есть
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }
  
        // Скопируйте оставшиеся элементы R[], если они есть
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }
  
    // Основная функция, которая сортирует arr[l..r] с помощью
    // функции merge()
    void sort(int arr[], int l, int r)
    {
        if (l < r) {
            // Найдите среднюю точку
            int m =l+ (r-l)/2;
  
            // Сортируем первую и вторую половины
            sort(arr, l, m);
            sort(arr, m + 1, r);
  
            // Объединить отсортированные половинки
            merge(arr, l, m, r);
        }
    }

Сложность алгоритма

Оценим быстродействие алгоритма: время работы определяется рекурсивной формулой O(n) = 2O(n/2) + ϴ(n). Ее решение: O(n) = nlogn – результат весьма неплох, учитывая отсутствие "худшего случая". Однако, несмотря на хорошее общее быстродействие, у сортировки слиянием есть и серьезный минус: она требует ϴ(n) памяти.

Достоинства и недостатки алгоритма сортировки слиянием

Достоинства:

• Работает даже на структурах данных последовательного доступа;
• Хорошо сочетается с подкачкой и кэшированием памяти;
• Неплохо работает в параллельном варианте: легко разбить задачи между процессорами поровну, но трудно сделать так, чтобы другие процессоры взяли на себя работу, в случае если один процессор задержится;
• Не имеет «трудных» входных данных;
• Устойчивая - сохраняет порядок равных элементов (принадлежащих одному классу эквивалентности по сравнению).

Недостатки:

• На «почти отсортированных» массивах работает столь же долго, как на хаотичных. Существует вариант сортировки слиянием, который работает быстрее на частично отсортированных данных, но он требует дополнительной памяти, в дополнении ко временному буферу, который используется непосредственно для сортировки;
• Требует дополнительной памяти по размеру исходного массива.