The Merge Sort algorithm is a sorting algorithm that is considered an example of the divide and conquer strategy. So, in this algorithm, the array is initially divided into two equal halves and then they are combined in a sorted manner. We can think of it as a recursive algorithm that continuously splits the array in half until it cannot be further divided. This means that if the array becomes empty or has only one element left, the dividing will stop, i.e. it is the base case to stop the recursion. If the array has multiple elements, we split the array into halves and recursively invoke the merge sort on each of the halves. Finally, when both the halves are sorted, the merge operation is applied. Merge operation is the process of taking two smaller sorted arrays and combining them to eventually make a larger one.

• Declare left variable to 0 and right variable to n-1
• Find mid by medium formula. mid = (left+right)/2
• Call merge sort on (left,mid)
• Call merge sort on (mid+1,rear)
• Continue till left is less than right
• Then call merge function to perform merge sort.

Algorithm:

step 1: start step 2: declare array and left, right, mid variable step 3: perform merge function. mergesort(array,left,right) mergesort (array, left, right) if left > right return mid= (left+right)/2 mergesort(array, left, mid) mergesort(array, mid+1, right) merge(array, left, mid, right) step 4: Stop

See the following C implementation for details.

MergeSort(arr[], l, r)

If r > l

• Find the middle point to divide the array into two halves:
  • middle m = l + (r – l)/2
• Call mergeSort for first half:
  • Call mergeSort(arr, l, m)
• Call mergeSort for second half:
  • Call mergeSort(arr, m + 1, r)
• Merge the two halves sorted in step 2 and 3:
  • Call merge(arr, l, m, r)

How Merge sort Works?

To know the functioning of merge sort, lets consider an array arr[] = {38, 27, 43, 3, 9, 82, 10}

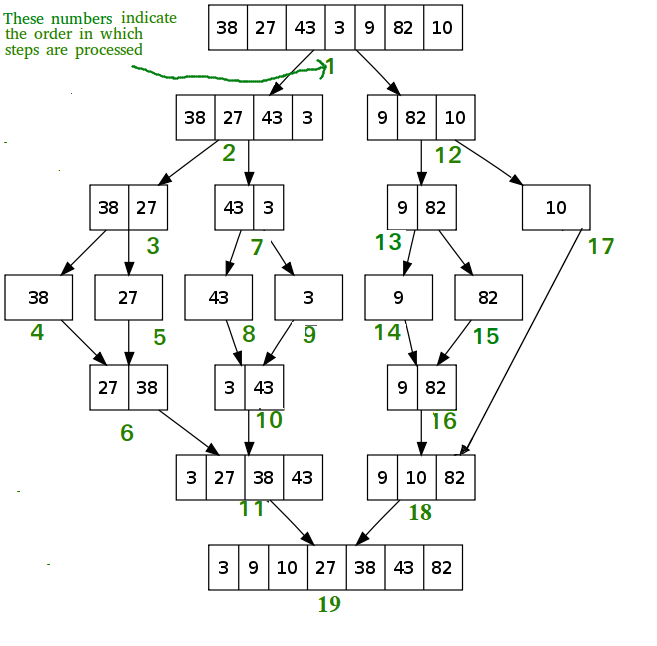
Merge Sort - Java Implementation

Merge Sort - Python Implementation

Output

Given array is 12 11 13 5 6 7 Sorted array is 5 6 7 11 12 13

Time Complexity:

O(n log(n)), Sorting arrays on different machines. Merge Sort is a recursive algorithm and time complexity can be expressed as following recurrence relation. T(n) = 2T(n/2) + θ(n)

The above recurrence can be solved either using the Recurrence Tree method or the Master method. It falls in case II of Master Method and the solution of the recurrence is θ(nLogn). The time complexity of Merge Sort is θ(nLogn) in all 3 cases (worst, average and best) as merge sort always divides the array into two halves and takes linear time to merge two halves.

Auxiliary Space: O(n)

Space Complexity : • In merge sort all elements are copied into an auxiliary array • so N auxiliary space is required for merge sort.

Algorithmic Paradigm: Divide and Conquer

Is Merge sort In Place? No in a typical implementation

Is Merge sort Stable: Yes, merge sort is stable.

Applications of Merge Sort:

• Merge Sort is useful for sorting linked lists in O(nLogn) time. In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike an array, in the linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore, the merge operation of merge sort can be implemented without extra space for linked lists. In arrays, we can do random access as elements are contiguous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in the linked list. Quick Sort requires a lot of this kind of access. In a linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have a contiguous block of memory. Therefore, the overhead increases for quicksort. Merge sort accesses data sequentially and the need of random access is low.

• Inversion Count Problem

• Used in External Sorting

Drawbacks of Merge Sort:

Slower comparative to the other sort algorithms for smaller tasks. The merge sort algorithm requires an additional memory space of 0(n) for the temporary array. It goes through the whole process even if the array is sorted. Recent Articles on Merge Sort Coding practice for sorting. Quiz on Merge Sort