1 - Logarithms 101

Logarithms or log: A mathematical concept/expression that’s used a lot in Computer Science and it’s the inverse (flip) of exponentials, and they’re used to answer the question: How many times must one “base” number be multiplied by itself to get some other particular number or (what power you have to raise to, to get another number) or we can also define it as The power (or exponent) to which one base number must be raised (multiplied by itself) to produce another number.

Example: How many times must a base of 20 be multiplied by itself to get 8,000? The answer is 3 (8000 = 20 × 20 × 20). So the logarithm base 20 of 8,000 is 3. It’s represented using a subscript (small number) to the lower right of the base number. So the statement would be log20(8,000) = 3.

log20(400) is like asking “How many 20s do we multiply to get 400? which is 2(20 * 20). So log20(400) = 2 Logarithms are defined using the following equation:

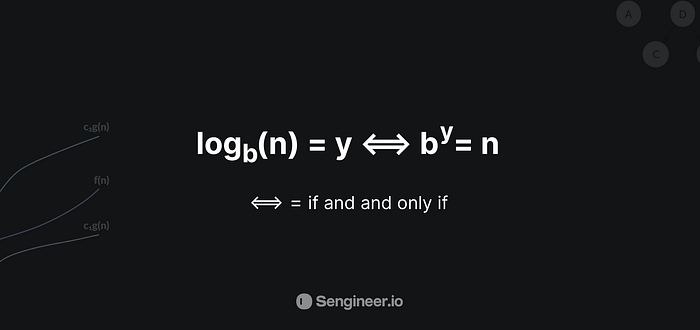
2 - Prerequisites that we need to understand

• Exponent: A number that identifies how many times that base number or expression must be multiplied by itself, it’s shown as a superscript (tiny number to the upper right of some other “base” number or mathematical expression).

• Base: in a logarithmic statement, a base number is a mathematical object to be multiplied by itself, and it’s expressed as a subscript to the lower right of the base number or by the number of times called for by an exponent, which is written as a superscript to the upper right of that base number

• Common logarithm: A logarithm that has a base number is 10. it’s used in measurements for sound, electricity, and light, etc…

• log: (in math) Abbreviation for logarithm.

• Binary logarithm: A logarithm where the base number is 2. Binary logarithms are the basis for the binary numeral system, it allows us to count using zero and one numbers only and they’re really important & very common in computer science.

3 - Computer science and Binary Logarithms

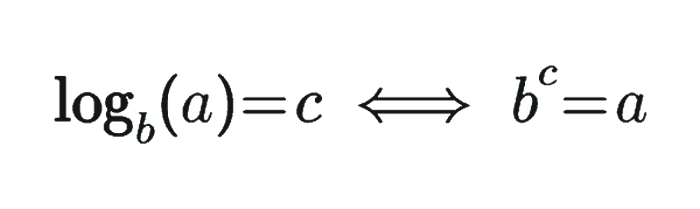
Initially, we have to understand something that may not have been obvious if you’ve seen the expression O(log n) before with regards to complexity analysis, when we talk about the logarithm, we have to specify a base.

So here the base is “b” and it’s denoted like a little “b” right below the log, and this is very important.

Because for example if we write log base 5 of number 10, and then we write log base 10 of number 10 we will get very different results because the equation would then be different. the “b” here would either be 5 or 10.

This is where we have to understand/realize that in computer science and coding interviews when we say log n of we always assume that the base is 2, assume that we’re dealing with what’s called the binary logarithm, which is a logarithm base 2 (as we’ve mentioned in the prerequisites) unless it’s specified to other bases.

4 - Why are logarithms in computer science are mostly Binary logarithms?

Because logarithms mostly occur in computer science by repeatedly dividing some data input (e.g. list, array, etc…) in half, which often occurs with algorithms like:

• divide-and-conquer algorithms like binary search, quicksort, Closest Pair of Points, Merge Sort, etc…

In those cases, the number of times you can divide a data input (e.g. list, array, etc…) of length n in half before you get down to single-element arrays is log₂ n.

and in computer science, exponential growth usually happens as a consequence of discrete processes like the divide-and-conquer we’ve mentioned. thus, we typically use log2 n as a logarithmic function, since it appears so frequently.

But just to clarify and not to confuse anyone, the fact that we use the binary logarithm most of the time, doesn’t imply that we always only use base 2 logarithms in Computer science. It’s just that it’s just common to work with binary numbers or divide input data in half, which is why base-two logarithms end up being the default in a lot of cases, and in general, it really doesn’t matter which base you choose. Because For example:

• in Big-O notation (Upper bound growth), all logarithms are asymptotically equivalent (the only difference is there multiplicative constant factor);

So we usually don’t even specify the base when writing something like O(log n) because we always assume that the logarithm is the binary logarithm meaning the log base 2, so we don’t even write the base 2 here.

P.s For those who have math background you’re probably used to using base 10 when you say log of N which is used in math typically.

if you’re used to this remember that for the purpose of computer science and coding interviews, you’re mostly always gonna be dealing with log base 2 unless it’s specified otherwise.

5 - The relation and what it means in terms of complexity analysis

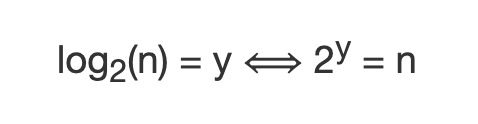
As we’ve mentioned before it basically means that log(n) is the power to which you need to put 2 to get “n”.

So logarithm base 2 of n would be equal to y if and only if the number 2 to the power of y were equal to n.

• For instance, this means that 1 is equal to the power that we need to put 2 to get one. and that power is 0. log(1) = 0 because 2 to the power of 0 is equal to 1: log(1) = 0 , 2⁰ = 1, other examples:
• The log of 8 would be: log(8) = 3, 2³ = 8
• The log of 16 would be: log(16) = 4, 2⁴ = 16

so to find the logarithm or the binary logarithm We have to ask ourselves, 2 to the power of what is equal to that number? And if we solve this then we find log n.

So what does this mean? 🙄

Let’s look at powers of two, When we increase a power of two, what we’re really doing is that we’re doubling whatever number we previously had, right?!

If we have the number 2 to the power of x, and we do 2 to the power of (x+1), we are multiplying that number by 2 or doubling it, right?

• Example: 2⁷ = 2⁶ · 2 Two to the power 6 is 64. 64 multiplied by two is 128, which is 2 to the power of 7. So, whenever we increase the exponent in two to the power of something by one, We are doubling that number. That’s really important.

In other words, when we double the number N, We are only increasing this question mark by one. So easy right! 🤞🎸

• Example #2: let’s suppose that we have 2⁴ = 16, and now you double 16, which is the number N here in the picture above, we double 16 to 32, and all we have to do is increase the exponent by one 2⁵ = 32 Recap: So as we can see in this relation picture, 2 to the power of question mark equals N. As N doubles the question mark only increases by one. Even when N is very big. And we can see this more clearly if we tried to increase the exponents by a bit more.

For instance, if we write out 2 to the power of 20. E.g. 2³⁰ =1,073,741,824 | 2⁴⁰ = 1,099,511,627,776 We increased the exponent only by 10.

So the purpose behind showing all of these examples is that the more N increases, the exponent or the question mark that is in the picture increases by a tiny amount, and since this relation, 2 to the power of ? equals N, is equivalent to log(n) = ?, and this tells us what log(n) really represents!

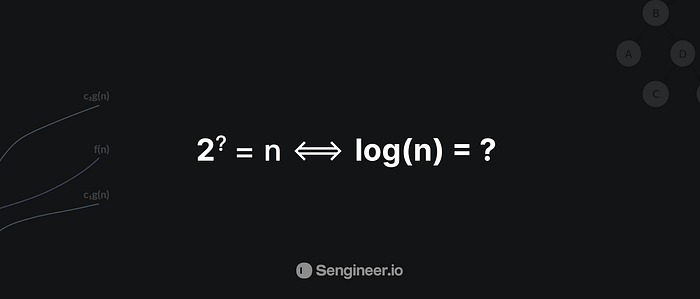
log(n) increases only by a tiny amount as N increases. When N doubles, log(n) only increases by 1. And so this is why, if we tie this back to complexity analysis when we have an algorithm with time complexity of log(n), that is incredibly good because that means as the input increases/doubles, the number of elementary operations that we’re performing in the algorithm only increases by one.

Logarithmic time complexity log(n): Represented in Big O notation as O(log n), when an algorithm has O(log n) running time, it means that as the input size grows, the number of operations grows very slowly. Example: binary search.

So I think now it’s clear for you that a log(n) complexity is extremely better than a linear complexity O(n). Even though O(n), linear time is already pretty good for an algorithm. log(n) time is gonna be way better as the size of your input increases.

6 - Comparing the logarithmic function vs. the linear function on the asymptote graph

if you’re familiar with the Big-O Complexity Chart you can see that the x-axis is here represents the number N.

a linear function complexity would look something like the O(n), where the complexity increase linearly with N.

• So when N is equal to let's say a billion. This line is gonna be at a billion;
• Whereas the O(log n) function, as you see in the asymptotic graph It goes up at the very beginning, as we’ve mentioned earlier that log(1) = 0 — log(4) = 2 — log(8) = 3.
• so it increases modestly at first, But then here the more the input gets bigger, (the more N increases) the less the log(n) function changes. Like we said up here when N is a million log(n) will only be 20.
• Even when N is gonna be a billion, log(n) is still only gonna be 30. It will have only increased by 20.

and that’s why log(n)is so powerful because the complexity of log(n) really represents a complexity that does not increase fast as the size of the input increases.

7 - The Final golden example: Binary search

P.s Binary search only can work only with sorted (Lists, Array, etc…)

Binary search is an efficient Interval Searching algorithm that can search sorted lists for the desired target.

Example:

• let’s suppose that we have a list of 1,024 elements and I have a number in mind that you have to guess in the fewest tries possible

• And with every guess, you get to know, if your guess was too high, too low, or correct.

• One approach you can use is to start guessing in a linear manner like saying: is it 0, if it was too low you will say 1, again if it was too low, you will say 2 and so on, and this approach is known as linear approach and based on what we know until now about the differences between the linear and the logarithmic time we can do better right?! Now the other (better) approach and instead of starting with the first element how about we start with the middle element, and if it was too low then, in that case, we eliminated half of the input right?! 😀

• So now after our guess was lower than the dried number and because we know that 0 until 512 are all lower than the number we want to guess, our next guess would be following the same approach, we half what’s left from the search space, and in that case, our second guess will be 768

• 768 was too high, but what happened again is that we cut down half of what’s left from the numbers in the search space

And this is how Binary search works It starts searching for the desired element in the middle of the input(Array, List, etc..), and then it moves to the right or left and depending on if the value you are looking for is bigger or smaller, and as we saw it reduces half of the remaining numbers in the search space at each iteration.

• So now in this case our next guess would be between 512 and 768
• So now instead of the 1,024 linear operations, we’ve seen in the case of linear search, it will take a max of 10 steps to get to the desired value we want with the Binary Search that has a logarithmic time complexity
• Another example: Let’s suppose that we’re looking for the desired value in a 1,073,741,824 items list, if we want to search for the value we want and it was at the end of the list, if we want to use the linear approach then we have to iterate 1,073,741,824 n times to get to the desired value. on the other hand, if we want to do this in a logarithmic fashion using binary search it would take us a max of log₂n 30 guesses, Mind-blowing right! 🤯 🎉

So now that we’ve got to know how binary search works, let’s see a code example, to solidify our understanding of the algorithm:

` const binarySearch = (list, target) => { let leftPointer = 0; // the beggining of the list let rightPointer = list.length - 1; // the end of the list

/* When leftPointer is bigger than rightPointer it means that the target we were looking for doesn't exist in the array so we return [] */ while (leftPointer < rightPointer) {

// Rounding down the middle pointer cause our input might not be perfect and we can't have decimal indexes
let middlePointer = Math.floor((leftPointer + rightPointer) / 2) 

let guess = list[middlePointer];

if (guess === target) { // Checking if the target we were looking for was present in the first iteration (Middle element)
  return middlePointer // if we found the item we return it
}
if (guess > target) {  // The guess was too high
  
  /*
    If the guess was too low or too high update the pointer accordingly, 
    which will reduce half the input in each iteration O(log₂n)
  */
  
  rightPointer = middlePointer--
} else {  // The guess was too low
  leftPointer = middlePointer++
}

} return [] }

console.log(binarySearch([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], 1)) `

And finally, since Binary Search divides the input in half at each iteration then it’s running in a logarithmic runtime: O(log n).

P.s. and in general, when we have an algorithm that divides the data in half on each call, we are most likely dealing with logarithmic runtime: O(log n).

Reference:

https://towardsdatascience.com/logarithms-exponents-in-complexity-analysis-b8071979e847